Introduction

Levitated optomechanics uses optical forces to suspend mesoscopic particles in vacuum. The confinement and translational motion of such trapped particles has seen extensive study in the last decade with major advances including parametric feedback cooling (FBC), zeptonewton force sensing and the realisation of cooling to the ground state of motion1,2,3,4,5,6. Hand-in-hand with these advances has been the study of the rotational degree of freedom where the levitated particle’s transverse motion is not only confined, but the particle is also free to spin about its centre-of-mass. Circularly polarised light possesses spin angular momentum. A beam of such polarisation can stably trap and continuously rotate mesoscopic particles: by reducing the ambient pressure in a levitated geometry in vacuum, extraordinarily high spin rates may be available when operating micron-sized birefringent particles in vacuum7. By extending to smaller particles, rotation rates of several GHz have recently been demonstrated8,9,10,11. These achievements provide access to a relatively unexplored physical regime. This may allow experiment to explore theoretically postulated quantum rotational effects, including quantum friction12,13,14,15. To progress this field further requires an understanding of the complex structure of the forces and torques acting on rapidly rotating particles in optical vacuum traps and the subsequent driven, stochastic motion.

Azimuthal spin forces (ASFs) are non-conservative. They derive from azimuthal components of (linear) optical momentum induced by inhomogeneous optical spin16,17,18 and are an ever-present feature of finite, circularly polarised optical beams. They have been shown to induce trapping instabilities for an isotropic particle in a circularly polarised trap19. For isotropic spheres the ASFs are appreciable in magnitude and, as one would expect, independent of orientation. They drive orbital rotations or limit cycles of the particle about the beam axis, the orbital angular momentum of which increases as viscous dissipation decreases, ultimately destabilising the trap when centripetal forces overcome gradient forces. For birefringent spheres the ASFs are also appreciable in magnitude. However, they are also strongly dependent on orientation. While isotropic spheres exhibit strongly unstable trapping dynamics, a seemingly contradictory observation is that a birefringent particle in a circularly polarised vacuum trap exhibits high stability in its motion7.

In this work, we explain the underlying physics for the inherent stability of motion for rotating birefringent particles in vacuum. The circular polarisation causes the birefringent particles to spin rapidly, resulting in an orientationally averaged effective ASF, several orders of magnitude lower than that of an isotropic sphere. Although greatly reduced, the residual ASF is sufficient to push the centre-of-mass motion of the particle well beyond equilibrium. The associated effects, which include stochastic orbital rotation and the subsequent formation of noisy, nano-scale limit cycles, become increasingly conspicuous with decreasing pressure. A key result of this paper concerns the application of FBC to these noisy limit cycles. Here, FBC involves modulating the optical forces in time, in such a way as to synthesise effective dissipative forces. This FBC-induced damping is sufficient to preserve the limit cycle, without introducing additional thermal fluctuations. Decreasing the ambient pressure reduces intrinsic thermal fluctuations, leaving a coherent, cooled limit cycle with an effective temperature on the order of milliKelvin.

Results and discussion

Overview of the experiment

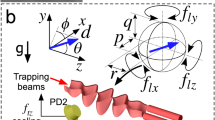
Isotropic spheres in circularly polarised vacuum traps are driven out of equilibrium and ultimately destabilised by non-conservative azimuthal forces deriving from optical spin momentum16,19. With decreasing pressure, the stable trapping point undergoes a Hopf bifurcation20, giving way to noisy limit cycles (or orbits) whose amplitude increases until the particle is ultimately ejected from the trap. These limit cycles consist of closed, roughly circular paths oriented normally with respect to the beam axis, which are executed by the particle, periodically, in a well defined time. In the experiment, these features are subject to the transverse and radial fluctuations caused by thermal fluctuations. Intriguingly, similar behaviour has not been previously observed for birefringent, vaterite particles, whose centre of mass motion was assumed to be conservative, and which are known to remain stably trapped even in high vacuum7.

Here we experimentally investigate this apparent discrepancy by analysing the centre-of-mass motion of a spinning vaterite particle in a circularly polarised trap under conditions of decreasing pressure. An overview of the key results is given in Fig. 1. In summary, we uncover behaviour analogous to that observed for isotropic spheres, signifying the active role of azimuthal spin forces. In comparison to isotropic spheres, however, the pressure required to form noisy limit cycles is about three orders of magnitude lower, and the dimensions of the limit cycles are about one order of magnitude lower. Application of FBC results in the formation of ultra-coherent, nano-scale limit cycle oscillations, with effective temperatures on the scale of milliKelivin.

Fig. 1: Overview of the experiment.
figure 1

Scatter plots of the x–y coordinates of the centre-of-mass of silica (blue) and vaterite (orange) microspheres before and after the Hopf bifurcation, without and with feedback cooling. The scale bar represents 200 nm and the centres of the distributions (marked as crosses) are positioned above the corresponding gas pressure, shown on the log scale below.

Full size image

Below, we provide more detailed analysis of the free running, and feedback cooled systems.

Free running experiments

Figure 2 describes the key features of the centre-of-mass motion of a spinning vaterite microsphere at higher (0.3 mbar) and lower (0.003 mbar) pressures. A more comprehensive set of results is provided in Supplementary Note S3. The radius of the microsphere is a = 2.2 μm, and the trap is a tightly focused circularly polarised beam of wavelength 1070 nm and numerical aperture 1.25. Details of the experimental set-up and tracking method are provided in Methods. The viscosity (μ, in Pa s) varies linearly with pressure (P in mbar) (Supplementary Note S4). For a sphere of the given radius,

$$\mu \simeq 3.56\times 1{0}^{-7}P.$$
(1)

The rate at which the vaterite sphere spins is inversely proportional to pressure and observed to be 100 kHz at a pressure of 0.01 mbar. For comparison, an analogous study, for a silica microsphere, is provided in Supplementary Note S2. At higher pressures ( ≈ 0.3 mbar), the centre-of-mass motion of spinning vaterite appears conservative (see Fig. 2a) since the spatial probability distribution is normal, (Fig. 2(c)) with kurtosis 2.9. However, the cross correlation (Fig. 2(e)) shows weak coupling between x and y coordinates, π/2 radians out of phase with the auto-correlation, indicating a slight tendency towards stochastic orbital motion of the centre-of-mass about the beam axis21. This is an explicitly non-conservative effect, reliant on azimuthal forces, demonstrating a departure from thermodynamic equilibrium. As the pressure is reduced, the probability distribution remains approximately normal (Supplementary Note S3) and the tendency towards orbital circulation, expressed by the amplitude of the cross correlation, grows. Further reduction of the pressure below 0.03 mbar causes the trapping point to undergo a Hopf bifurcation leaving a noisy limit cycle20, characterised by an annular probability distribution (Fig. 2(b, d)), and a cross-correlation with amplitude ~ 0.8 and a decay time, τD ≈ 170 ms, equivalent to ≈ 85 × 103 time periods (Fig. 2(f)). This behaviour is directly analogous to that observed for isotropic silica spheres of similar dimensions (Supplementary Note S4), although the pressures required for limit cycle formation are approximately three orders of magnitude lower for spinning vaterite and the dimensions of the limit cycles are one order of magnitude lower.

Fig. 2: Experimentally measured centre-of-mass motion of spinning vaterite particles at pressures of 0.3 mbar and 0.003 mbar.
figure 2

Spatial probability distributions in the x–y plane (a, b) are projected onto x (c, d) together with the auto (orange) and cross (yellow) correlations, i.e. Cxx = 〈x(t)x(t + τ)〉 and Cxy = 〈x(t)y(t + τ)〉 (e, f).

Full size image

Theoretical model

To understand the dramatic quantitative differences between the motion of vaterite and silica microspheres we consider a simple numerical model (see Supplementary Note S4). With reference to the schematic, Fig. 3(a), the particle is at mechanical equilibrium when its symmetry axis, \(\hat{{{{{{{{\bf{u}}}}}}}}}\), is parallel to the transverse, x–y plane, and the centre-of-mass is downstream of the focal point, so that the weight of the particle is balanced by the upward radiation pressure. An optical torque, τz, causes it to spin with equilibrium angular frequency Ωs = τz/ξr for rotational drag ξr = 6πμa. Figure 3(b) shows the azimuthal force, fϕ(r, α), as a function of radial position, r, and orientation, α. This component depends strongly on orientation, changing sign for ranges of α, and can be well approximated by a low order Fourier series, e.g. \({f}_{\phi }(r,\alpha )\approx {a}_{0}(r)+{a}_{2}(r)\sin (2\alpha )+{b}_{2}(r)\cos (2\alpha )\) (where a0 is much smaller than a2 or b2). As a consequence, the ASF acting on the particle oscillates at the spinning frequency, Ωs. In contrast, the gradient force is approximately independent of α, and linear for r ⪅ 1 μm with stiffness coefficient k.

Fig. 3: Theoretical model.
figure 3

(a) Schematic showing a birefringent microsphere held in a circularly polarised (CP) optical trap. The co-ordinate system denotes the Cartesian co-ordinates by x, y and z and the polar co-ordinates by r and ϕ. \(\hat{{{{{{{{\bf{u}}}}}}}}}\) is the particle’s symmetry axis and α and β describe the particle’s orientation relative to the trap centre. Calculated values of the (b) azimuthal force, fϕ(r, α) as a function of radial coordinate, r, and orientation, α, and (c) orientationally averaged azimuthal forces for a birefringent vaterite sphere (biref), an equivalent isotropic sphere with the same mean index of refraction (iso) and as silica (Si). Steady state spatial probability distributions simulated using rotationally averaged forces in (d) the x–y plane and (e) projected onto the x coordinate.

Full size image

The motion of the particle depends qualitatively on the relative frequencies of the spinning (Ωs) and translational (\({\Omega }_{{{{{{{{\rm{o}}}}}}}}}=\sqrt{k/m}\)) motions (see Supplementary Note S4). Here, we are primarily interested in the low pressure regime where Ωs ≫ Ωo. Under these conditions, conservation of angular momentum increasingly confines the symmetry axis, \(\hat{{{{{{{{\bf{u}}}}}}}}}\), to the transverse x–y plane and oscillations of the azimuthal force, caused by the particle spinning, are too rapid to couple with the motion of the centre-of-mass (Supplementary Note S4). As a result, the dynamical motion of the centre-of-mass is determined by rotationally averaged, effective forces, \(\langle \, {f}_{r/\phi }(r)\rangle =\int\nolimits_{0}^{2\pi }{f}_{r/\phi }(r,\alpha )d\alpha\). The effective ASF, 〈 fϕ(r)〉, is strongly suppressed in comparison with isotropic particles, contains non-linearities close to the beam axis and changes sign at r ≈ 0.2 μm (see Fig. 3(c)).

It is instructive to ignore thermal fluctuations and consider the underlying deterministic motion of the particle. At higher pressures, viscous damping prevents the centripetal forces acquired by the particle, from the non-conservative ASFs, from exceeding the optical gradient forces19. This ensures the stability of the trapping point. At lower pressures, limit cycles (or orbits) can form in which gradient and centripetal forces are balanced in the radial direction and azimuthal forces are balanced by viscous drag,

$$mr{\Omega }_{{{{{{{{\rm{o}}}}}}}}}^{2}={f}_{r}(r)\approx kr,$$
(2a)
$${\xi }_{t}{\Omega }_{{{{{{{{\rm{o}}}}}}}}}r={f}_{\phi }(r).$$
(2b)

In addition to these equilibrium conditions (Eq. (2)), stability conditions (Supplementary Note S6) must also be satisfied. These latter conditions define the curvature in the force field required to ensure that perturbations from the limit cycle decay with time. For spinning vaterite, this curvature appears close to the beam axis, explaining the lower radius of the orbits in comparison to those formed for silica (Fig. 3(c)). Application of the equilibrium and stability conditions to the averaged force profiles predicts stable, deterministic limit cycles, emerging for pressures below ≈ 0.06 mbar, with radii in the range ro ≈ 0.1 → 0.15 μm, which remain mechanically stable for arbitrarily low pressures.

The above considerations determine the stability of deterministic trajectories. To understand the effect of thermal fluctuations we integrate the stochastic, Langevin equations of motion, Eq. (3),

$$\langle {{{{{{{\bf{f}}}}}}}}(r)\rangle +{{{{{{{{\bf{f}}}}}}}}}^{L}(t)-mg\hat{{{{{{{{\bf{z}}}}}}}}}-{\xi }_{t}\dot{{{{{{{{\bf{r}}}}}}}}}=m\ddot{{{{{{{{\bf{r}}}}}}}}},$$
(3a)
$$\langle {{{{{{{{\bf{f}}}}}}}}}^{L}(t)\rangle =0,\,\,\langle {{{{{{{{\bf{f}}}}}}}}}^{L}(t)\otimes {{{{{{{{\bf{f}}}}}}}}}^{L}({t}^{{\prime} })\rangle =2{k}_{{{{{{{{\rm{B}}}}}}}}}T{\xi }_{t}\delta (t-{t}^{{\prime} }),$$
(3b)

with rotationally averaged forces. Probability densities, similar to those observed experimentally, are obtained Fig. 3(d, e). These simulations suggest that the trap remains thermally stable to pressures below ≈ 3 × 10−4 mbar (see also Supplementary Note S5).

Parametric feedback cooling

Theoretical considerations

Conceptually, the aim of FBC is to augment the intrinsic viscous forces in a stochastic system (e.g. Eq. (4a)), without modifying the variance of the fluctuating forces. Obviously, this modified system does not satisfy the fluctuation-dissipation theorem (Eq. (3b)).

$${\xi }_{t}\to {\xi }_{t}^{{\prime} }=({\xi }_{t}+{\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}),$$
(4a)
$$T\to {T}^{{\prime} }=T{\xi }_{t}/({\xi }_{t}+{\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}),$$
(4b)

However, by applying the transformations, Eq. (4), to the Langevin equation, Eq. (3), (where \({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\) is a feedback-induced drag coefficient), we see that the system with perfect feedback is equivalent to a new, effectively autonomous, system which satisfies the fluctuation-dissipation theorem with increased drag, Eq. (4a), and a rescaled temperature, Eq. (4b).

Most commonly, FBC is applied to conservative systems which satisfy the Boltzmann distribution at steady state. Since this distribution is independent of viscosity, the only effect of FBC on the steady state distribution is an effective reduction in temperature, Eq. (4b). Here, we apply FBC to non-equilibrium steady states (NESS), associated with a non-conservative system. In this case, probability distributions generally depend on viscosity20 as well as temperature. Thus, the influence of FBC on steady state conditions can only be understood by combining both Eqns. (4) with steady state probability distributions which, for NESS, are seldom known a priori. For this reason, care must be taken in estimating effective temperatures in such systems22. In order to arrive at an internally consistent estimate we analyse both radial fluctuations and phase diffusion about the cycle.

Our implementation of FBC is described in the Methods. Additional damping is synthesised by modulating the optical power in response to measurements of the particle position. The magnitude of the feedback induced damping, \({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\), depends on the efficiency of the feedback loop. Initially, \({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\) increases as the intrinsic Stokes drag and associated thermal fluctuations are decreased. Thereafter it approaches a limit imposed by the time delays and other imperfections in the system. This principle determines the variation of the effective drag, \({\xi }_{t}^{{\prime} }\) and temperature \({T}^{{\prime} }\), Eq. (4) with viscosity and therefore pressure (Eq. (1). As pressure is reduced, \({\xi }_{t}^{{\prime} }\) initially increases as \({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\) increases. Ultimately, the Stokes drag, ξt becomes negligible and \({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\) attains its limiting value, so that the effective drag, \({\xi }_{t}^{{\prime} }\), saturates. The variation of the effective temperature, \({T}^{{\prime} }\) in Eq. (4b), is dominated by decreases in the Stokes drag, ξt, so that it decreases continuously with decreasing pressure, approaching linearity i.e. \({T}^{{\prime} }\approx T{\xi }_{t}/{\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\), for low pressure with constant \({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}\).

Experimental results

With these considerations in mind, we explore the effect of FBC on the non-equilibrium centre-of-mass motion of our rapidly spinning vaterite particles. Figure 4 describes the effect of applying FBC simultaneously to the x, y and z motions of optically trapped spinning vaterite microspheres.

Fig. 4: Experimentally measured stochastic trajectories of a vaterite microsphere in a circularly polarised trap with feedback damping.
figure 4

Particle position distribution in the x–y plane at different gas pressures of (a) 0.29 mbar, (b) 0.03 mbar, (c) 0.0033 mbar. Envelope of the cross correlation 〈x(t)y(t + τ)〉 at different gas pressures with decay times of 13.8 s (0.29 mbar), 37 s (0.03 mbar) and 416 s (0.0033 mbar), compared with a orbital time period of 2 ms (d). Mean orbital radius \(\bar{r}\), (e), and (f) variance of radial fluctuations \(\overline{ \langle {(r-{r}_{{{{{{{{\rm{o}}}}}}}}})}^{2}\rangle}\), where ‘FB’ (orange) denotes a feedback cooled particle and ‘no FB’ (blue) denotes a particle without feedback cooling. Phase diffusion of feedback cooled limit cycles accrued over time intervals, Δt, normalised by gas pressure in mbar (g). Results for three different pressures are shown, P = 0.01, 0.003, 0.001 mbar.

Full size image

Figure 4(a–c) show spatial probability distributions at pressures of 0.29, 0.03 and 0.003 mbar for feedback cooled vaterite particles. Decreasing pressure results in dramatic clarification of the underlying limit cycle, as indicated by the cross correlations, Fig. 4(d), whose amplitudes approach unity with decay constants equivalent to ≈ 2 × 105 orbital time periods at a pressure of 3.3 × 10−3 mbar. The underlying deterministic cycles are approximated by fitting general closed curves, ro(ϕ), to the noisy data (Supplementary Note S7) allowing us to compute first the mean radius of the cycle, \(\bar{{r}_{{{{{{{{\rm{o}}}}}}}}}}=\frac{1}{2\pi }\int\nolimits_{-\pi }^{\pi }{r}_{{{{{{{{\rm{o}}}}}}}}}(\phi )d\phi\), (Fig. 4(e)) and next the variance of the fluctuations transverse to the cycle (Fig. 4(f)).

The parameters of these limit cycles can be used to quantify the effective forces operating in the feedback cooled system. Balancing radial forces, Eq. (2a), gives the limit cycle frequency, \({\Omega }_{{{{{{{{\rm{o}}}}}}}}}\approx \sqrt{{k}_{{{{{{{{\rm{fb}}}}}}}}}/m}\), where kfb is the stiffness including any modifications caused by feedback. Since Ωo is unchanged, the influence of feedback on the trap stiffness is negligible (i.e. kfb ≈ k). Eq. (2b) describes the relationship between the limit cycle dimensions and the drag forces acting on the particle. Similarly, balancing azimuthal forces, Eq. (2b), suggests that the limit cycle will constrict with increasing drag, due to the form of the effective ASF (Fig. 3(c)). This effect is shown in Fig. 4(e), consistent with the previous assertion that the total drag, \(({\xi }_{t}+{\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}})\), increases initially before approaching a limiting value as the pressure is reduced. Figure 4(f) examines the cycle averaged variance in the radial fluctuations, \(\overline{\langle {(r-{r}_{{{{{{{{\rm{o}}}}}}}}})}^{2}\rangle }\), with and without feedback (see Supplementary Note S7 for details). We see that the cooled radial fluctuations are proportional to P, and therefore to the effective temperature, \({T}^{{\prime} }\). The notion of temperature in single particle NESSs is controversial22 and cannot usually be directly related to quantities such as \(\overline{\langle {(r-{r}_{{{{{{{{\rm{o}}}}}}}}})}^{2}\rangle }\). However, by necessity \(\overline{\langle {(r-{r}_{{{{{{{{\rm{o}}}}}}}}})}^{2}\rangle }\) = 0 for T = 0, and we expect \(\overline{\langle {(r-{r}_{{{{{{{{\rm{o}}}}}}}}})}^{2}\rangle }\propto T\) for small T19. These caveats notwithstanding, \(\overline{\langle {(r-{r}_{{{{{{{{\rm{o}}}}}}}}})}^{2}\rangle }\) decreases linearly with pressure, by ~ 4 orders of magnitude at a pressure of 3.3 × 10−3 mbar, implying an effective temperature \({{{{{{{\mathcal{O}}}}}}}}(10){{{{{{{\rm{milliKelvin}}}}}}}}\).

Further insight into the stochastic dynamics can be obtained by considering the phase diffusion about the limit cycle. Since limit cycles are neutrally stable, diffusion along a limit cycle resembles diffusion in a constant force field23,24. For an approximately circular limit cycle with radius \(\bar{{r}_{{{{{{{{\rm{o}}}}}}}}}}\), at long times, the variance of the displacement of the phase satisfies Eq. (5a),

$$\langle {\left(\phi (\Delta t)-\bar{\phi }(\Delta t)\right)}^{2}\rangle \sim \left\{\begin{array}{lll}\frac{2{k}_{{{{{{{{\rm{B}}}}}}}}}T}{{\bar{{r}_{{{{{{{{\rm{o}}}}}}}}}}}^{2}{\xi }_{t}}\Delta t,\hfill &\,{{\mbox{No FB}}}\,&(5{{{{{{{\rm{a}}}}}}}}) \\ \frac{2{k}_{{{{{{{{\rm{B}}}}}}}}}T{\xi }_{t}}{{\bar{{r}_{{{{{{{{\rm{o}}}}}}}}}}}^{2}{({\xi }_{t}^{{{{{{{{\rm{fb}}}}}}}}}+{\xi }_{t})}^{2}}\Delta t,\hfill &\,{{\mbox{FB}}}\,&(5{{{{{{{\rm{b}}}}}}}})\end{array}\right.$$

where we have defined the phase simply by the azimuthal coordinate, accumulated continuously as the cycle is repeatedly traversed. The expression for phase diffusion with feedback, Eq. (5b), can be obtained either by applying the transformations, Eq. (4), or through formal integration (Supplementary Note S8). In the low pressure limit with feedback, we have \(\langle {\left(\phi (\Delta t)-\bar{\phi }(\Delta t)\right)}^{2}\rangle \propto {\xi }_{t}\Delta t\). This relationship is confirmed in Fig. 4(g), for time intervals t ≲ 0.1 s, and should be compared with the result for unperturbed limit cycles, Eq. (5a), which has the inverse dependence on ξt. For larger intervals, Δt ≳ 0.1, phase diffusion saturates, suggesting that the particle motion, along the limit cycle, synchronises with the time modulation of the optical forces25. These observations support the notion that the statistics of feedback cooled, non-equilibrium states can be understood in terms of the effective temperature and modified drag given in Eq. (4), given prior knowledge of the general form of the statistics we are interested in (Eq. (5), for example).

Conclusions

As we have shown, the azimuthal forces acting on vaterite particles, trapped in circularly polarised vacuum traps, depend strongly on orientation and can even reverse their direction so that they oppose the direction of the spin momentum16 in the incident field. This counter-intuitive and seemingly paradoxical behaviour has been observed in other systems18,26, and can often be explained by considering the momentum in both the incident and scattered optical fields. Rapid rotation of vaterite microspheres results in effective azimuthal forces that are strongly suppressed and highly non-linear. This combination of properties explains the huge quantitative differences observed for birefringent and isotropic microspheres. In both cases, reductions in pressure (i.e. viscosity) destabilise the trap, which undergoes a bifurcation leading to limit cycle formation. For vaterite particles, however, the suppression of the effective ASF means that the pressure at which this transition takes place is four orders of magnitude lower than it is for silica, while the non-linearity accounts for the reduction in size of the limit cycles formed. Our results show that objects of intermediate dimensions can be stabilised in circularly polarised traps by selecting or designing particles with appropriate effective ASFs (see Supplementary Note S10), allowing for the design of larger rotors carrying greater centripetal loads required e.g. for testing fundamental material properties27,28. To illustrate this point, Supplementary Note S9 describes how dramatic improvements in stability can be obtained by tuning the length of a silicon microrod held in a circularly polarised counter-propagating beam trap.

Crucially, the effective azimuthal force is non-linear close to the beam axis, within the linear range of the gradient force. This unique characteristic allows us to cool these limit cycles to effective milliKelvin temperatures. FBC increases the effective drag acting on the particle, which shrinks the limit cycle towards a limit. In addition, the reduction in effective temperature suppresses thermal fluctuations, exposing nano-scale limit cycles of exceptional clarity. We analyse both the transverse fluctuations and phase diffusion about the cycle to give estimates of the effective temperature on the order of ≳ 1 milliKelvin. Extensions of this approach could enable cooling towards the quantum regime, which could allow experimental realisation of quantum synchronisation, macroscopic entanglement of mesoscopic bodies or, more generally, the study of the non-equilibrium stochastic thermodynamics of self-sustained oscillators29,30,31,32.

Although ASFs decrease rapidly for particle sizes approaching the dipole limit33 (see Supplementary Note S10), the effects we describe are otherwise generic, and will necessarily manifest themselves in other systems e.g. nanodumbells or microrods10,34 (see Supplementary Note S9). We also note that all circularly polarised beams carry azimuthal components of momentum, while the corresponding forces may be small or suppressed depending on the particle’s size, shape and material, they can never be perfectly negated. The effects reported here are therefore generic, and are guaranteed to appear for sufficiently low damping.

Methods

Sample preparation

Vaterite is a positive uniaxial birefringent material in a spherical morphology. The synthesis of vaterite microspheres with a mean radius of 2.20 μm ± 0.02 μm (2σ) is reported elsewhere7. NIST-traceable size standards of silica with a diameter of 5.1 ± 0.5 μm (Thermo Scientific 9005) are used to compare their dynamics with birefringent microspheres.

Sample loading

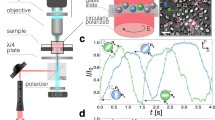
We use a small vacuum chamber with a volume of 27.7 μℓ and an annular piezoelectric transducer (APC International Ltd., Cat. no.70-2221) attached to the chamber to load microspheres into the optical trap. Before conducting the trapping experiments, dried microspheres are applied to the surface of optical glass windows (Harvard Apparatus Ltd., CS-8R: 8 mm in diameter, 150 μm in thickness) of the chamber. Once sealed, the chamber pressure is reduced to ~ 100 mbar. The piezoelectric transducer is operated at 140 kHz to detach microspheres from the glass surface, while a high numerical aperture microscope objective (Nikon Ltd., E Plan 100 × , NA = 1.25/oil) focuses a circularly polarised trapping beam (continuous wave 1070 nm) in the vacuum chamber. When a single particle is trapped, the piezoelectric transducer is switched off, and the chamber pressure is further reduced to < 1 mbar to provide parametric feedback control. The optical power can be adjusted to 10−25 mW to obtain the desired trap frequency from 0.4 kHz to 1.1 kHz.

Particle position detection

The particle motion is tracked by a quadrant photodiode (QPD) array (First Sensor, QP50-6SD2, −3dB at 150 kHz). To calibrate the QPD response to nanometer displacements, we used a nano-positioning stage (PI, P-733.3 XYZ) with an orientated vaterite microsphere adhered to the surface of the glass coverslip. First, the trapping beam is focused onto the centre of the stuck microsphere. Next, the forward scattered light from the microsphere is directed onto the QPD, and its voltage reading is recorded at ten-nanometer increments along the x and y directions. Then, the measurement is repeated at different orientations from 0 to π with a π/8 step. As a result, we obtain eight different values of the QPD voltage dependence with respect to displacement (see Supplementary Note S1). Because the vaterite microsphere rotates at a rate ( ≫ 10 kHz) that is orders of magnitude larger than the trap frequencies ( ~ 0.5 kHz) for gas pressures < 0.1 mbar, the QPD voltage response can be averaged over the angles. As a result, we obtain a mean dependence of 5.59 mV nm−1 with a position sensitivity of 2.0 nm in its linear range (see Fig. S1(b)).

Feedback control and phase-locked loop

In order to perform FBC experiments, the interference pattern of the forward scattered light from a trapped microsphere is projected at the back focal plane of an imaging objective onto the QPD, yielding three voltage signals corresponding to the microsphere’s x, y and z motion (see calibration of QPD above).

The QPD signals are processed by a lock-in-amplifier (Zurich Instruments, HF2LI, 210 MSa/s, DC − 50 MHz) to extract the oscillation frequencies (ωx, ωy, ωz) and their phases (ϕx, ϕy, ϕz) of the particle oscillation. A frequency-doubled waveform with an adjusted phase shift relative to the particle oscillation for each direction is superimposed as \(\Sigma {A}_{i}\sin (2{\omega }_{i}t+{\phi }_{i}+\delta {\phi }_{i})\), where i = x, y, z to the voltage waveform driving an acousto-optic modulator (IntraAction, DTD-274HD6M) to modulate the trap intensity (≤ ± 5%). For limit cycle oscillations, ωx = ωy ≡ Ωo and the modulation in response to transverse motions is simply \(A\sin (2{\Omega }_{{{{{{{{\rm{o}}}}}}}}}t+{\phi }_{{{{{{{{\rm{o}}}}}}}}}+\delta {\phi }_{{{{{{{{\rm{o}}}}}}}}})\).