Abstract
Classical and reverse substituent effects were studied for pyrrole derivatives. Two extensive sets of pyrrole derivatives with NO, NO2, CN, CF3, COMe, COOH, CHO, CONH2, Cl, SH, SiH3, F, PH2, H, Me, OMe, OH, NH2, NHMe, NMe2, Li, BeH, BH2, Na, MgH, and AlH2 substituents at N and C3 positions were taken into account. Analysis of the substituent effects was based on charges of the Substituent Active Region (cSAR). The cSAR values were obtained from atomic charges calculated within the Quantum Theory of Atoms in Molecules (QTAIM) methodology. Calculations were performed at the B3LYP/6-311++G** level of theory. It was documented that classical substituent effect in substituted pyrroles is much greater (approximately ten times) for substituents at C3 position than at NH group. The reverse substituent effect is also greater in C3-substituted pyrroles that in N-substituted ones. As a result of observed correlations, substituent constants for some rare substituents such as Li, BeH, BH2, Na, MgH, and AlH2 were evaluated.
Similar content being viewed by others
Introduction
Classical understanding of the substituent effects has been introduced by Hammett [1] as an influence of one chemical group X, named a substituent, on chemical properties of another one named as the reaction site Y in systems like X-R-Y, where R is a transmitting moiety. It was an ingenious idea to define numerical values of substituent effect by introducing a concept of substituent constants σ defined as Eq. 1:
Where, K(X) and K(H) are dissociation constants measured in water in standard conditions for substituted and unsubstituted benzoic acid derivatives, respectively.
The next step was an assumption, that the substituent effect on acid/base equilibria of benzoic acid derivatives is similar to the substituent effects in other chemical reactions, including those controlled kinetically. It was described by the so-called Hammett equation, Eq. 2:
Where, ρ is the so-called reaction constants describing sensitivity of the reactions characterized by equilibrium or rate constants (K or k) to the substituent effect.
In a later application, Eq. 2 has been used for interpretation of various physicochemical properties [2–9]. However, even in the original Hammett book [1], it was stated that the substituent constant σ for NO2 group is different for dissociation of para-substituted derivatives of benzoic acid and aniline: 0.78 and 1.27, respectively. Then, for electron-attracting groups like NO2, CN, COOH, and CHO, new substituent constants σ* were introduced for describing substituent effects when reaction site is electron donating [2]. By the next 50 years, a great development in the field of substituent effect studies has been observed. In consequence, numerous scales and interpretations of substituent constants have appeared [6, 8, 10–14]. They are dependent on the nature of interaction of the substituent in question (X) with the remainder part of the substituted systems (R-Y). Now, it can be stated that there are two faces of the substituent effects. First, the classical one, as that defined by the Hammett Eq. (2), where the properties of the chemical group named reaction site Y are affected by another group named substituent X. Interpretation of the changes in physicochemical properties involves the substituent constants (σ) and the reaction constant (ρ). The other face of intramolecular interactions described as substituent effects is named reverse substituent effect. This means that electron-donating/electron-attracting properties of X depend on the kind of R-Y part of the molecule [15–17]. A great number of various substituent constants (see a complete collection of them in [13]) are just a result of this kind of interactions. It simply means that the electron-donating (ED) or electron-attracting (EA) properties of a substituent X depend on a position and kind of a molecule to which X is attached. The aforementioned various substituent constants are secondary substituent constants [11] and comprise a few sources of errors: (i) the error of experimental measurements, (ii) the error associated with an assumed model, and (iii) the error of standardization (via a linear regression analysis) of the measured experimental data to the scale of Hammett’s constants. None of the above completed empirical scales of substituent constants [13] may be effective in so many situations realized in practice—most often, substituent constants are taken for further work by some kind of intuition or by analogy with better known cases.
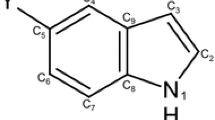
In previous theoretical studies of the substituent effect on properties of monosubstituted (at the nitrogen atom) pyrrole and benzene derivatives, their geometrical and electronic characteristics were analyzed; some results were discussed based on electronegativity of the substituents [18]. A novel approach to the substituent effect, which also allows quantitative estimation of the reverse substituent effect, is based on a concept of charge of the Substituent Active Region (cSAR) introduced by Sadlej-Sosnowska [19, 20]. cSAR(X) is a sum of atomic charges of X and of the ipso atom (carbon or nitrogen in our case) to which the substituent is attached. It was shown that cSAR(X) values correlate well [15, 19–22] with the Hammett substituent constants [13]. Moreover, it was documented that cSAR of a functional group (NO and NMe2) in para-substituted derivatives of nitrosobenzene and N,N-dimethylaminebenzene nicely describes changes in the geometry in these groups [23]. It was also shown that in many cases cSAR(X) estimated by use of various methods of atomic charge assessments leads to comparable results [24]. The aim of this paper is to show how application of cSAR concept may be successfully used for describing classical and reverse substituent effects in N- and C3-substituted pyrrole derivatives presented in Scheme 1.
Computational details
Geometries of all analyzed compounds were optimized without any symmetry constrains at the B3LYP/6-311++G** computational level using Gaussian 09 software [25]. Equilibrium natures of all calculated geometries were checked by frequency calculations.
Atomic charges, necessary for cSAR value calculations, were obtained by integration of atomic basins within the frame of the Quantum Theory of Atoms in Molecules [26]. We also tested other methods of population analyses, like NBO [27] and Hirshfeld [28] charges. All of them provide similar variability of cSAR values, as it was observed in the previous study [24]. Atoms in Molecules (AIM) charges were found as characterized by a slightly greater variability, what is advantageous for correlation analysis. Thus, AIM charges were chosen for presentation. The value of the integrated Laplacian within the atomic basin is a measure of accuracy of the Atoms in Molecules calculations and should ideally be equal to 0. However, values of the integrated Laplacian smaller than 1.0 × 10−3 for all the atoms of a molecule have been described as the ones to generate negligible errors [29]. Thus, it was assumed that the charge integration is accurate enough if the Laplacian values are below this limit. Atomic charges were calculated by the AIMAll package [30].
Results and discussion
For clarity, the obtained cSAR values for N- or C3-substituted pyrroles are denoted as cSAR(NX) and cSAR(C3X), respectively. In C3-substituted pyrrole derivatives, the NH group may be considered as a reaction site; therefore, dependence of cSAR(NH) on cSAR(C3X) represents a classical substituent effect. The difference from the exact Hammett treatment is an application of the cSAR(C3X) as a quantitative descriptor of substituent effect instead of substituent constants; whereas, cSAR(NH) represents property of the reaction site.
Figure 1 shows a well-correlated (R 2 = 0.949) dependence of cSAR(NH) on cSAR(C3X) for C3-substituted pyrroles. The negative slope indicates that the increase of charge at the NH group is related to the decrease of the charge at the substituent X. A very important characteristic of the regression line is its low value of the slope (−0.082). Beyond doubt, this is associated with differences in ranges of cSAR values of the amino group which is ca. 0.05 of cSAR unit, whereas changes in cSAR values for the C3X fragment are ca. ten times greater and equal to ~0.6 of cSAR unit! This may be interpreted by the fact that the lone pair of the NH group is only scarcely involved in changes of EA/ED properties of the substituents.
When cSAR(X) values estimated for pyrroles, substituted at C3 and N atoms, and for benzene ring, are plotted against substituent constants, the results are correlated, as shown in Fig. 2. The regression lines have much worse determination coefficients than the former one (Fig. 1) but are very impressive. The regression lines for C3-substituted pyrroles and for benzene derivatives are very similar (slopes are −0.177 and −0.185, respectively). The conclusion is that the changes in EA/ED properties of substituents attached to the C3 position in pyrrole and to benzene are almost identical. In the case of N-substituted species, the dependence is weaker with the slope of −0.099 and with much lower determination coefficient.
The reverse substituent effect in N- and C3-substituted pyrrole derivatives may be shown by dependence of cSAR(NX) on cSAR(C3X) values, as presented in Fig. 3. This dependence shows how differently, in a quantitative meaning, the pyrrole moiety affects substituents attached at the N and C3 atoms. The regression has an acceptable determination coefficient (R 2 = 0.903); and hence, the slope is a reliable quantity. Its value is 0.882 and this means that substituted moiety affects EA/ED properties of substituents attached to the C3 atom stronger than those attached to the N atom, which is in line with the data shown in Fig. 2.
Additionally, it is well known that energy of HOMO can be considered as a convenient descriptor of propensity to oxidation of the system. It was documented by good correlations between HOMO of aromatic hydrocarbons and polarographic half-wave potential of oxidation [31, 32]. Dependences of HOMO energies on the cSAR(X) estimated for substituents attached at N and C3 atoms of pyrrole are presented in Fig. 4. The relations between LUMO energies and cSAR values are also shown there but they are not conclusive; however, those for HOMO are worth consideration.
The obtained dependences of HOMO on cSAR(C3X) and cSAR(NX) indicate that substituents attached to the nitrogen atom affect HOMO values more clearly than those attached to the C3 one. The shapes of HOMO orbitals for N- and C3-substituted pyrroles differ significantly, as shown in Fig. 5 for selected pyrrole derivatives (substituents with the lowest and the highest values of σ p constants). Thus, HOMO orbitals for pyrrole as well as its N(CH3)2 and NO derivatives are presented. In the case of C3 series, a substituent dramatically changes HOMO shape in comparison to that observed for pyrrole and its N-substituted systems. It resulted in better correlation of the HOMO energies with N-derivatives than with C3 ones. Thus, in this way, oxidative power of these systems is documented. In the case of monosubstituted benzene derivatives, no acceptable correlation (R 2 = 0.476) between HOMO energies and cSAR(X) values was found.
The cSAR values obtained for substituted benzenes and pyrroles at the N and C3 atoms are presented in Table 1. The estimated standard deviation (esd) values are very similar for benzene and C3-substituted pyrrole systems; whereas, in the case of N-substituted pyrroles, this value is smaller. Contrary to that, the substituent effects on NH group in C3-substituted pyrroles are very small. This indicates that electronic structure of NH group is very weakly affected by substituents at the C3 position.
Finally, due to the linear correlation between σ p and cSAR(C3X) (see Fig. 2), it was possible to estimate approximate values of substituent constants (σ p ) of such unusual substituents as Li, BeH, BH2, Na, MgH, and AlH2. These values are presented in Table 1 with asterisks.
Conclusions
Charge of the cSAR approach was applied to study substituent effect in substituted pyrroles which was compared with the effect observed in monosubstituted benzenes. The obtained results demonstrate the following:
-
1.
Substituent effect in substituted pyrroles is much greater (~ten times) for substituents attached at C3 position than for NH group.
-
2.
The electron-donating/electron-attracting properties of substituents attached at C3 position are practically identical with those observed in the monosubstituted benzene derivatives.
-
3.
The reverse substituent effect is more pronounced in C3-substituted systems than in N-substituted ones.
-
4.
The propensity to oxidation is more dependent on substituent effects for N-substituted systems than for C3 ones.
Furthermore, application of the correlation between cSAR(X) and σ p values allowed estimation of approximate values of substituent constants for such unusual substituents as Li, BeH, BH2, Na, MgH, and AlH2. This is an important example of the potential application of the cSAR(X) concept.
References
Hammett LP (1940) Physical organic chemistry. McGraw–Hill, New York
Jaffe HH (1953) Chem Rev 53:191–261
Zuman P (1967) Substituent effects in organic polarography. Plenum Press, New York
Exner O (1972) In: Chapman NB, Shorter J (eds) Advances in linear free energy relationships. London, Plenum Press
Johnson CD (1973) The Hammett equation. Cambridge University Press, Cambridge
Shorter J (1991) In: Zalewski RI, Krygowski TM, Shorter J (eds) Similarity models in organic chemistry, biochemistry and related fields. Amsterdam, Elsevier
Williams A (2003) Free energy relationships in organic and bioorganic chemistry. Royal Society of Chemistry, Cambridge
Krygowski TM, Stępień BT (2005) Chem Rev 105:3482–3512
Exner O, Bohm S (2006) Curr Org Chem 10:763–778
Charton M (1973) Prog Phys Org Chem 10:81–204
Exner O (1978) In: Chapman NB, Shorter J (eds) Correlation analysis in chemistry—recent advances. New York, Plenum Press
Charton M (1981) Prog Phys Org Chem 13:119–251
Hansch C, Leo A, Taft RW (1991) Chem Rev 91:165–195
Exner O, Krygowski TM (1996) Chem Soc Rev 25:71–75
Siodla T, Oziminski WP, Hoffmann M, Koroniak H, Krygowski TM (2014) J Org Chem 79:7321–7331
Krygowski TM, Oziminski WP (2014) J Mol Model 20:2352–2360
Stasyuk OA, Szatylowicz H, Krygowski TM, Fonseca Guerra C (2016) Phys Chem Chem Phys 18:11624–11633
Zborowski K, Alkorta I, Elguero J (2007) Struct Chem 18:797–805
Sadlej-Sosnowska N (2007a) Polish J Chem 81:1123–1134
Sadlej-Sosnowska N (2007b) Chem Phys Lett 447:192–196
Krygowski TM, Sadlej-Sosnowska N (2011) Struct Chem 22:17–22
Szatylowicz H, Siodla T, Stasyuk OA, Krygowski TM (2016) Phys Chem Chem Phys 18:11711–11721
Sadlej-Sosnowska N, Krygowski TM (2009) Chem Phys Lett 476:191–195
Stasyuk OA, Szatylowicz H, Fonseca Guerra C, Krygowski TM (2015) Struct Chem 26:905–913
Gaussian 09, Revision A.02, Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ (2009) Gaussian, Inc., Wallingford
Bader RWF (1990) Atoms in molecules: a quantum theory. Clarendon Press, Oxford
Weinhold F, Landis CR (2005) Valency and bonding. Cambridge University Press, Cambridge, A natural bond orbital donor-acceptor perspective
Hirshfeld FL (1977) Theor Chim Acta 44:129–138
Alkorta I, Picazo O (2005) Arkivoc ix: 305.-320
AIMAll, Version 11.10.16, Keith TA (2011) TK Gristmill Software, Overland Park (aim.tkgristmill.com)
Lund H (1957) Acta Chem Scand 11:1323–1330
Streitwieser Jr A (1961) Molecular orbital theory for organic chemists. J. Wiley & Sons, New York
Acknowledgements
Thanks are given to “ICM” Warsaw computer center (project number G17-8) for an allocation of computer time. H.S. and T.M.K. thank the National Science Centre and Ministry of Science and Higher Education of Poland for supporting this work under the grant no. UMO-2013/11/B/ST4/00531.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Dedicated to the memory of our friend Klaus Albert (1947–2017), retired professor at the University of Tuebingen.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zborowski, K.K., Szatylowicz, H., Stasyuk, O.A. et al. Towards physical interpretation of substituent effects: the case of N- and C3-substituted pyrrole derivatives. Struct Chem 28, 1223–1227 (2017). https://doi.org/10.1007/s11224-017-0938-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11224-017-0938-7