Ab initio symmetry-adapted emulator for studying emergent collectivity and clustering in nuclei

Introduction

Ab initio approaches to nuclear structure and reactions (for an overview, see Ref. [1]) aim to provide accurate predictions based on few-nucleon forces, such as the ones derived from chiral effective field theory (EFT) [for a review, see e.g. Ref. [2] and references therein]. To achieve this, it is imperative to utilize high-precision nuclear forces that accurately describe nuclear correlations, from short- to long-range correlations, as well as to quantify uncertainties that arise from the nuclear force and the controlled approximations in solving the many-body Schrödinger equation [3]. Such developments use statistical tools, including, for example, Bayesian analysis [4], global sensitivity methods [5], and uncertainty estimates based on regression [6, 7], that sometimes require a large number of computationally intensive calculations which often poses a challenge.

In this paper, we seek to overcome some of these difficulties by combining the symmetry-adapted no-core shell model (SA-NCSM) framework [8–10] with the methodology of eigenvector continuation (EVC) [5, 11, 12]. The SA-NCSM uses a physically relevant basis that, in manageable model spaces, achieves descriptions of light to medium-mass nuclei, including challenging nuclear features, such as collectivity, clustering, and related continuum effects. Similarly, EVC further reduces the sizes of Hamiltonian matrices by mapping them onto much smaller matrices referred to as emulators, low-dimensional manifolds built upon a set of characteristic solutions to the many-body Schrödinger equation. The proposed symmetry-adapted eigenvector continuation (SA-EVC) method opens the door to calculations up through the medium-mass region and studies of collective and clustering nuclear features that otherwise might be computationally infeasible.

With a view toward inferring new knowledge of the nuclear forces relevant to structure and reaction observables, we construct novel SA-EVC emulators to study collective and clustering nuclear properties in ⁶Li and ¹²C (an emulator for the ⁶Li binding energy is validated in Ref. [13]). Because this study focuses on the method validity, we utilize SA-NCSM calculations for a single harmonic oscillator (HO) strength ℏΩ, for which and for a specific parameterization of the chiral potential we show that the observables under consideration converge with the number of HO excitations, including point-proton root-mean-square (rms) radii and E2 transitions. The SA-NCSM utilizes a symplectic Sp(3,$\mathbb{R}$)-adapted basis and selected model spaces¹ that are significantly reduced in size due to symmetry considerations without sacrificing the physics of interest. Moreover, we show that the set of chiral potential parameterizations used to train the emulators has no significant effect on dominant nuclear features such as the nuclear shape (and associated symplectic symmetry) and cluster formation, making the SA model spaces highly suitable for this study. However, from one parameterization to another we find that probability amplitudes of wave functions and cluster peak distance vary slightly, affecting by a factor of two or less collective quadrupole moments, asymptotic normalization coefficients (ANCs), and alpha partial widths (which provide the probability for the alpha decay among all possible decays of a state). This suggests that these types of observables, and associated emulators, are important to inform and construct the nuclear forces for high-precision nuclear calculations.

Theoretical methods

Ab initio symmetry-adapted no-core shell model

Ab initio large-scale calculations [8, 9] have recently revealed a remarkably ubiquitous and almost perfect symmetry, the Sp(3,$\mathbb{R}$) symplectic symmetry, in nuclei that naturally emerges from first principles up through the calcium region (anticipated to hold even stronger in heavy nuclei [14]). Since this symmetry does not mix nuclear shapes, this novel nuclear feature provides important insight from first principles into the physics of nuclei and their low-lying excitations as dominated by only one or two collective shapes—equilibrium shapes with their vibrations—that rotate (Figure 1A).

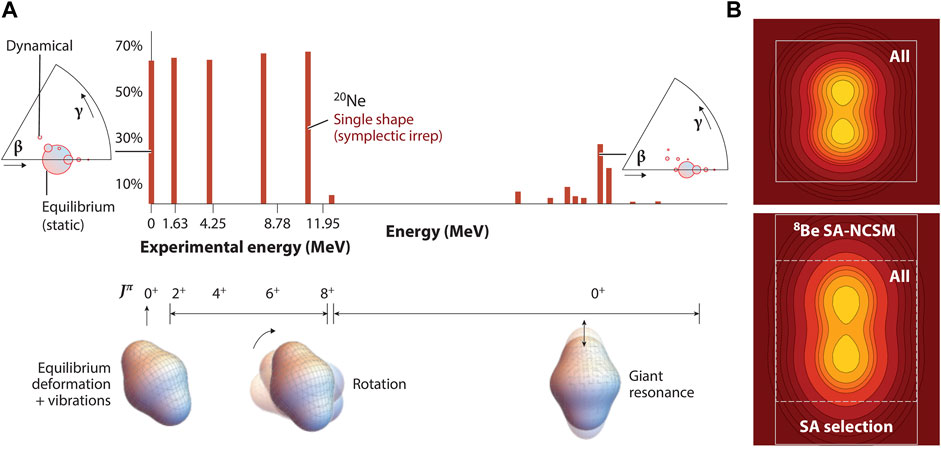
FIGURE 1. (A) Emergent symplectic symmetry in nuclei: Contribution of the most dominant shape to the 0⁺ ground state of ²⁰Ne and its rotational band (2⁺, 4⁺, 6⁺, and 8⁺), as well as to excited 0⁺ states, pointing to a fragmented giant monopole resonance [8]; for selected states, the deformation distribution within a shape is shown in terms of the shape parameters, the average deformation β and triaxiality angle γ (based on ab initio SA-NCSM calculations with NNLO_opt in a model space of 11 HO shells with ℏΩ = 15 MeV inter-shell distance). (B) Schematic illustration of the SA concept shown for ⁸Be: a smaller model space (square) includes all possible shapes (labeled as “All”) and yields spatially compressed wave functions (top); a larger model space (rectangle in lower panel) accommodates, in a well prescribed way, spatially extended modes (“SA selection”) that are neglected in smaller model spaces. Figure from Ref. [9] under the terms of its CC BY license.

The SA-NCSM theory [8, 10, 15] capitalizes on these findings and exploits the idea that the infinite Hilbert space can be equivalently spanned by “microscopic” nuclear shapes and their rotations [or symplectic irreducible representations (irreps), subspaces that preserve the symmetry], where “microscopic” refers to the fact that these configurations track with the position and momentum coordinates of each particle. A collective nuclear shape can be viewed as an equilibrium (“static”) deformation and its vibrations (“dynamical” deformations) of the giant-resonance type, as illustrated in the β-γ plots of Figure 1A [8, 16]. A key ingredient of the SA concept is illustrated in Figure 1B, namely, while many shapes relevant to low-lying states are included in typical shell-model spaces (Figure 1B, top), the vibrations of largely deformed equilibrium shapes and spatially extended modes like clustering often lie outside such spaces. The selected model space in the SA-NCSM remedies this, and includes, in a well prescribed way, those configurations. Note that this is critical for enhanced deformation, since spherical and less deformed shapes, including relevant single-particle effects, easily develop in comparatively small model-space sizes.

In this study, we utilize the ab initio SA-NCSM theory [8–10] that is based on the NCSM concept [17, 18] with nuclear interactions typically derived from the chiral EFT (e.g. [2, 19–23]). We use SA-NCSM model spaces, which are reorganized to a correlated basis that respects the shape-preserving Sp (3,$\mathbb{R}$) symmetry and its embedded symmetry, the deformation-related SU(3) [8–10]. We note that while the model utilizes symmetry groups to construct the basis and calculate matrix elements, descriptions are not limited a priori to any symmetry and can account for significant symmetry breaking.

The SA-NCSM is reviewed in Refs. [9, 10] and has been applied to light and medium-mass nuclei using SU(3)- and Sp(3,$\mathbb{R}$)-adapted bases. The many-nucleon basis states of the SA-NCSM are constructed using efficient group-theoretical algorithms and are labeled according to SU(3) × SU(2) by the proton, neutron and total intrinsic spins, S_p, S_n, and S, respectively, and (λ_ω μ_ω) quantum numbers with λ_ω = N_z − N_x and μ_ω = N_x − N_y, where N_x + N_y + N_z = N₀ + N, for a total of N₀ + N HO quanta distributed in the x, y, and z directions². Here, N₀ℏΩ is the lowest total HO energy for all particles (“valence-shell configuration”) and NℏΩ (N ≤ N_max) is the additional energy of all particle-hole excitations. Thus, for example, (λ_ω μ_ω) = (0 0), for which N_x = N_y = N_z, describes a spherical configuration, while N_z larger than N_x = N_y (μ_ω = 0) indicates prolate deformation. In addition, a closed-shell configuration has (0 0). Indeed, spherical shapes, or no deformation, are a part of the SA basis. However, most nuclei—from light to heavy—are deformed in the body-fixed frame, which for 0⁺ states appear spherical in the laboratory frame.

Furthermore, considering the embedding symmetry Sp(3,$\mathbb{R}$) ⊃SU(3), one can further organize SU(3) deformed configurations into subspaces that preserve Sp(3,$\mathbb{R}$) symmetry. Each of these subspaces (symplectic irrep, labeled by σ) is characterized by a given equilibrium shape, labeled by a single deformation N_σ(λ_σ μ_σ). For example, the symplectic irrep N_σ(λ_σ μ_σ) = 0(8 0) in ²⁰Ne consists of a prolate 0(8 0) equilibrium shape (static deformation) with λ_ω = 8 and μ_ω = 0 in the valence-shell 0p-0h (0-particle-0-hole) subspace, along with many other SU(3) deformed configurations or dynamical deformation (vibrations), such as N_ω(λ_ω μ_ω) = 2(10 0), 2(6 2), and 8 (16 0), which include particle-hole excitations of the equilibrium shape to higher shells [8, 14, 16]. These vibrations are multiples of 2ℏΩ 1p-1h excitations of the giant-resonance monopole and quadrupole types, that is, induced by the monopole $r^2={\sum }_{i=1}^A{\vec{r}}_i\cdot {\vec{r}}_i$ and quadrupole $Q_2=\sqrt{16\pi /5}{\sum }_{i=1}^A{r}_i^2{Y}_2({\widehat{r}}_i)$ operators, respectively (for further details, see Refs. [10, 24]).

An advantage of the SA-NCSM is that the SA model space can be down-selected from the corresponding ultra-large N_max complete model space to a subset of SA basis states that describe static and dynamical deformation, and within this SA model space the spurious center-of-mass motion can be factored out exactly [25, 26]. Another benefit is the use of group theory for constructing the basis and calculating matrix elements, including the Wigner-Eckart theorem, which allows for calculations with SU(3) reduced matrix elements that depend only on (λ μ), along with computationally efficacious group-theoretical algorithms and data structures, as detailed in Refs. [27–31]. A third advantage is that deformation and collectivity are examined and treated in the approach without the need for breaking and restoring rotational symmetry. The reason is that basis states utilize the SU(3)_{(λ μ)} ⊃ SO(3)_L reduction chain that has a good orbital angular momentum L, whereas all SU(3) reduced matrix elements can be calculated in the simpler canonical SU(3)_{(λ μ)} ⊃ SU(2)_I reduction chain (for details, see Refs. [32, 33]). The canonical reduction chain provides a natural reduction to the x and y degrees of freedom, it is simple to work with, and most importantly, provides a complete labeling of a basis state that includes the single-shell quadrupole moment eigenvalue that measures the deformation along the body-fixed symmetry z-axis [34]. SU(3) reduced matrix elements calculated within this scheme yield, in turn, matrix elements for the SA-NCSM basis by invoking the Wigner-Eckart theorem with the appropriate SU(3)_{(λ μ)} ⊃ SO(3)_L Clebsch-Gordan coefficients that are readily available [32].

We emphasize that all basis states are kept up to some $N_{\text{max}}^{\mathrm{C}}$, yielding results equivalent to the corresponding $N_{\text{max}}^{\mathrm{C}}$ NCSM calculations. Building upon this complete $N_{\text{max}}^{\mathrm{C}}$ model space, we expand the model space to N_max by adding selected basis states to include only the necessary vibrations of largely deformed equilibrium shapes that lie outside this $N_{\text{max}}^{\mathrm{C}}$ (such SA-NCSM model spaces are denoted as $⟨N_{\text{max}}^{\mathrm{C}}⟩N_{\text{max}}$).

Eigenvector continuation method in the symmetry-adapted framework

As introduced in Ref. [11], the EVC method utilizes the fact that if a Hamiltonian is a smooth function of some real-valued parameters, its eigenvectors will also be well-behaved functions of those parameters. In practice, this means that one can use a relatively small number of known wave functions to construct an accurate emulator well-approximated by a low-dimensional manifold, and with it accurately predict observables for an arbitrary chiral potential parameterization [12]. To compute these initial wave functions from first principles, it is advantageous to use SA model spaces that can accommodate deformation, including spatially expanded modes, as well as medium-mass regions.

An advantage of the EVC method is that solutions are achieved by diagonalizing matrices with sizes that are many orders of magnitude smaller than those used in exact calculations. This results in a drastically reduced computational time with practically no discrepancies from the exact results. EVC thus provides a means of generating large samples of nuclear observables from variations in the Hamiltonian parameters. This, in turn, makes computationally intensive statistical analyses, such as sensitivity studies [5, 12], possible. It also allows for a reduced computational load for quantifying uncertainties of ab initio predictions.

In this study, we construct emulators capable of probing collective and clustering features by employing the EVC method with SA model spaces. As illustrated in Table 1, the SA-NCSM reduces the sizes of Hamiltonian matrices by up to four orders of magnitude, or equivalently by more than 97%. The application of EVC to these SA spaces results in an additional reduction of up to 3 more orders of magnitude, or as much as 99%. In this combined framework, the final size of the resulting matrices are as much as 10^–5 times smaller than they would be in the corresponding N_max complete spaces. As the first step, we consider a chiral EFT nucleon-nucleon (NN) interaction truncated at next-to-next-to-leading order (NNLO), which depends on 14 low-energy constants (LECs). It turns out that we can write the chiral Hamiltonian as $H(\vec{c})={\sum }_{i=0}^{14}{c}_i{h}_i$, where $\vec{c}$ is a vector representing a unique combination of the LECs, h_i are the constituent chiral potentials, h₀ is the LEC-independent part of the chiral potential plus relative kinetic energy and the Coulomb interaction, and c₀ = 1.

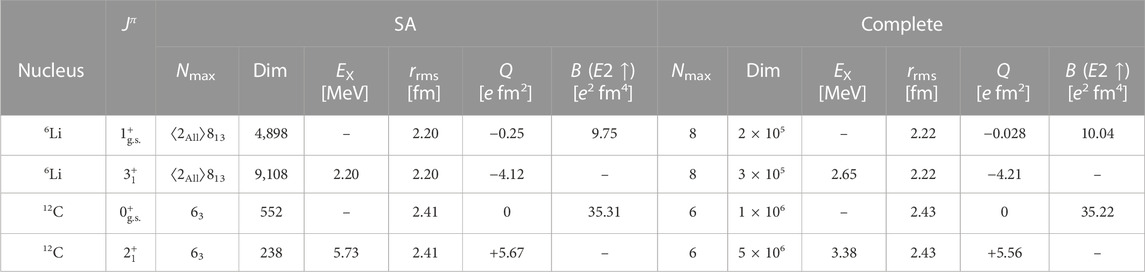
TABLE 1. Model space dimensions (labeled as “Dim”), excitation energy E_X, point-proton rms radius r_rms, electric quadrupole moment Q, and B (E2 ↑) transition strengths from the ground state (g.s.) to the first excited state of ⁶Li and¹²C, calculated with NNLO_opt and ℏΩ = 15 MeV in SA and complete model spaces. ⟨2_All⟩8₁₃ denotes an N_max = 2 model space with all symplectic irreps (complete), 13 Sp (3,$\mathbb{R}$) irreps of which extend to N_max = 8; 6₃ denotes 3 Sp (3,$\mathbb{R}$) irreps up to N_max = 6.

A state $|\psi (\vec{c})\rangle$ can be well-approximated as a linear combination of known “training” wave functions ${\sum }_j^{N_T}{\alpha }_j(\vec{c})|\psi ({\overrightarrow{c_T}}_j)\rangle$, where each $|\psi ({\overrightarrow{c_T}}_j)\rangle$ in this study is the lowest-energy eigenvector of $H({\overrightarrow{c_T}}_j)$ for a given J^π, $\overrightarrow{c_T}$ corresponds to a training point in the LEC parameter space, and N_T is the number of training points. The chiral Hamiltonian matrices h_i are constructed in the representation of the training wave functions. These N_T × N_T matrices are used to emulate the wave function for any set of LECs $\vec{c}$ by solving the Schrödinger equation for the unknown ${\alpha }_j(\vec{c})$ as a generalized eigenvalue problem that uses the norm matrix for the training wave functions, $M_{ij}=⟨\psi ({\overrightarrow{c_T}}_i)|\psi ({\overrightarrow{c_T}}_j)⟩$.

The new features here are that we generate the emulator for the electric quadrupole moment Q by constructing the Q matrix in the representation of the training eigenvectors (as done for rms radii in Ref. [5]), and that these are calculated using SA model spaces. The quadrupole moment is then approximated by computing $⟨\psi (\vec{c})|Q|\psi (\vec{c})⟩={\sum }_{ij}{\alpha }_i(\vec{c}){\alpha }_j(\vec{c})⟨\psi ({\overrightarrow{c_T}}_i)|Q|\psi ({\overrightarrow{c_T}}_j)⟩$.

Results and discussions

The results presented in this paper use the SA-NCSM in an Sp(3,$\mathbb{R}$) basis with an NN chiral potential up to NNLO as used in [21]. The consistent treatment of NN and three-nucleon (3N) forces at this order is feasible but outside the scope of the present study, which aims to show the validity of the SA-EVC method. We also include the outcomes for a specific NN parameterization, NNLO_opt [21], for which the 3N forces have been shown to contribute minimally to the 3- and 4-nucleon binding energy [21]. Furthermore, the NNLO_opt NN potential has been found to reproduce various observables, including the ⁴He electric dipole polarizability [35]; the challenging analyzing power for elastic proton scattering on ⁴He, ¹²C, and ¹⁶O [36]; neutron-deuteron scattering cross-sections [37]; along with B (E2) transition strengths for ²¹Mg and ²¹F [38] in the SA-NCSM without effective charges.

For the EVC calculations, we use N_T = 32 training points within the 14-dimensional parameter space for NNLO. We restrict the ranges of the LECs to lie within ±10% of their values for NNLO_opt [21] and adopt the regularization for NNLO_opt. We sample training points using a randomly seeded latin hypercube design, and validate the emulators for 256 points that are different from the training points but within the same range of the LECs.

The SA-EVC results start with SA model spaces that are reduced by three to four orders of magnitude compared to the corresponding N_max complete model space (or, equivalently, NCSM calculations), as outlined in Table 1. Moreover, the associated observables are in good agreement for SA and complete model spaces, with differences that are typically comparable to differences resulting from varying ℏΩ (see Ref. [8], supplemental material). Specifically, for the example of NNLO_opt, we report in Table 1 excitation energies, point-proton rms radii, electric quadrupole moments, and B (E2 ↑) transition strengths between the two lowest energy states of ⁶Li and ¹²C. We also show that for the SA spaces used to train the emulators all of the above observables are converged with N_max (Figure 2).

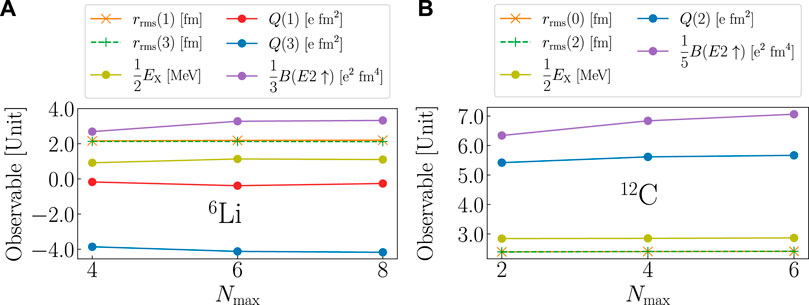
FIGURE 2. Convergence with N_max of the quadrupole moments Q(J), point-proton rms radii r_rms(J), excitation energies E_X, and B (E2 ↑) transition strengths for the two lowest-lying states in (A) ⁶Li and (B) ¹²C. Observables are computed with the NNLO_opt parameterization for ℏΩ = 15 MeV in SA model spaces reported in Table 1.

Thus, for example, as shown in Table 1, collectivity-driven observables agree within 0.3%–2.9%, and radii agree at the sub-percent level. The largest deviation is observed for the ⁶Li 1⁺ quadrupole moment, however, it is important that its sign and very small magnitude are reproduced in both calculations. Furthermore, such differences are expected to decrease in richer model spaces; indeed, in a series of benchmark studies for light nuclei such as ⁴He, ⁶Li, ¹²C, and ¹⁶O (reviewed in Ref. [9]), we have shown that the SA-NCSM uses significantly smaller model spaces in comparison to the corresponding large complete N_max model spaces without compromising the accuracy for various observables (including electron scattering form factors [39] and sum rules [35]), as well as for effective inter-cluster potentials [31]. Reference [9] has also shown that for light nuclei, the SA-NCSM is in reasonable agreement with other ab initio approaches, such as hyperspherical harmonics [40, 41], the NCSM [17, 18], and quantum Monte Carlo [42].

Collectivity and clustering of training wave functions

An important feature of the training wave functions is that the dominant deformed configurations, or the SU(3) content of the states under consideration, remain practically the same for all of the training wave functions (Figure 3). In addition, the SU(3) content agrees with the probabilities obtained with NNLO_opt in the corresponding N_max complete model space, also shown in Figure 3. This ensures that the same static and dynamical deformed modes govern the physics for all LECs sets under considerations, thereby justifying the use of the same SA selection for all the training wave functions.

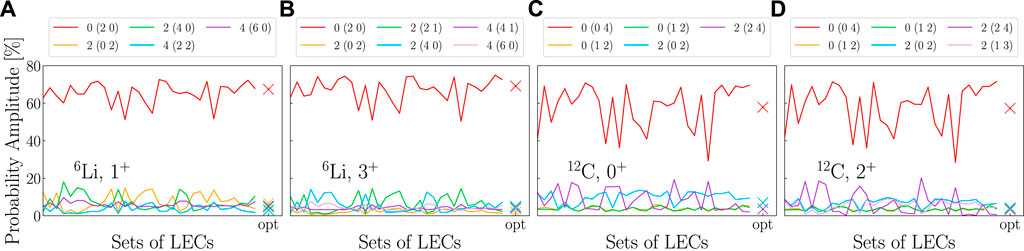
FIGURE 3. The largest SU (3) probability amplitudes (solid lines) as a function of emulator training LECs sets for (A) ⁶Li 1⁺ ground state and (B) ⁶Li $3_1^{+}$ state in N_max = ⟨2_All⟩8₁₃ model space [all SU(3) states have $\{S_{\mathrm{p}},S_n,S\}=\{\frac{1}{2},\frac{1}{2},1\}$], as well as for (C) ¹²C 0⁺ ground state and (D) ¹²C $2_1^{+}$ state in N_max = 6₃ [all SU(3) states have {S_p, S_n, S} = {0, 0, 0} except for 0 (1 2) with {S_p, S_n, S} = {0, 1, 1} (orange) and {1, 0, 1} (green)]. Results are also shown for the NNLO_opt parameterization in the corresponding N_max complete model space (labeled as “opt”).

Specifically, we find that one SU(3) irrep dominates the dynamics of each state at the 50%–60% level, with several additional configurations each contributing from 1% to 20% depending on the LECs set. Moreover, when the basis states are further organized into Sp(3,$\mathbb{R}$) irreps, we find that a single symplectic irrep—which contains the dominant SU(3) configurations—contributes at practically the same level from one training wave function to another. For example, the (2 0) symplectic irrep in ⁶Li accounts for 83%–88% of each 1⁺ training wave function, whereas the (2 0) contributes at the 85%–88% level in the case of the 3⁺, out of thirteen available different irreps. Similarly, the probability of the (0 4) irrep in each of the ¹²C training ground states is between 80%–88%, and between 82%–94% for the first 2⁺ states. This is a strong indicator that the emulators are trained on wave functions that retain the symmetry-preserving and symmetry-breaking patterns that are observed in nuclei [8] and that the SA model spaces used in this study are sufficient to capture nuclear collectivity. Indeed, the fact that the Sp(3,$\mathbb{R}$) symmetry remains a near perfect symmetry for each of the training wave functions, retaining the same shape from one wave function to another, further supports the use of SA selections in the EVC method, or otherwise, the SA model spaces would need to be re-examined.

Another important feature of the training wave functions is that cluster formation is largely unaffected by the choice of interaction parameters. To study this, we project the ⁶Li states onto the α + d system, following Ref. [43]: we use a ground state for each cluster that is renormalized to the most dominant SU(3) configuration, and we adopt R-matrix theory to match the amplitude of the cluster wave function and its derivative to those of the exact Coulomb eigenfunctions at large distances. We note that we are primarily interested in the effect of the LECs on the correlations in the training wave functions; hence, we fix the threshold energy to the experimental one. For the ³S₁ partial wave, we observe about 20% variations in the calculated asymptotic normalization coefficients (C₀ = 1.45–2.07 fm^−1/2) around their average value and 10% variations in the spectroscopic factor, namely, SF = 0.75–0.90 (Figure 4A). This tracks with the ±10% variation in the LECs. For comparison, the NNLO_opt ANC for this particular channel is C₀ = 1.77 fm^−1/2 with SF = 0.87. Interestingly, the height of the second peak, which is located near the nuclear surface and informs the probability of cluster formation, remains fixed for all the parameterizations and coincides with the one for the NNLO_opt case, only its position slightly varies with the LECs.

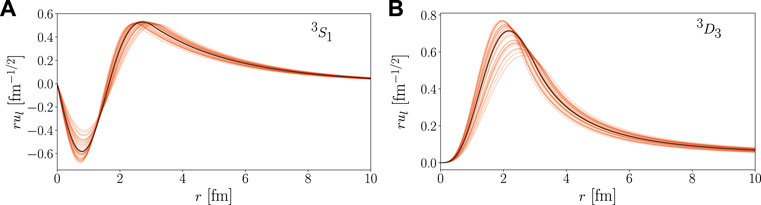
FIGURE 4. α + d (A) ³S₁-wave and (B) ³D₃-wave as functions of the relative distance r, computed from the ⁶Li training wave functions for SA model spaces reported in Table 1. The spread of the curves is given by the ± 10% variation in the LECs. The case for NNLO_opt is shown in black.

While the ³D₃ spectroscopic factors (SF = 0.73–0.92, with 0.90 for NNLO_opt) vary approximately at the 15% level (Figure 4B), which is practically the same as for the ³S₁ partial wave, α widths of the 3⁺ state range from Γ_α = 6.34 keV–14.05 keV, which is about ±40% from Γ_α = 9.81 keV calculated for this particular channel with NNLO_opt (similarly to the ANCs, we use the experimental threshold energy). We note that the NNLO_opt values for C₀ and Γ_α are reported for a single channel without taking excitations of the clusters into account (e.g., see Ref. [44]) and should not be compared directly to experiment. Of particular interest for this study is that the LECs sets induce a change in both the location and magnitude of the peak, to which the probability for alpha decay is typically sensitive to.

To summarize, the behavior of the surface peaks in both channels and the nuclear shapes of the 1⁺ and 3⁺ states in ⁶Li (as well as the shapes of the 0⁺ and 2⁺ states in ¹²C) are relatively consistent. This suggests that the terms of the nuclear potential that are independent of the LECs, including parts of the long-range interaction, are largely responsible for cluster formation, along with the development of the nuclear shape [equivalently, almost perfect Sp(3,$\mathbb{R}$) symmetry]. In contrast, the LECs, which capture the unresolved short-ranged interactions between nucleons, fine-tune collective and clustering features, and affect the associated observables by only a factor, namely, 1.4 for the $1_{\mathrm{g}.\mathrm{s}.}^{+}$ ANCs, 2.2 for the $3_1^{+}$ alpha width, and 1.4 for the $3_1^{+}$ quadrupole moment in ⁶Li. Similarly, the quadrupole moment for the $2_1^{+}$ in ¹²C is affected by a factor of 2.1. While the clustering features are explored in this study for the training points only, the SA-EVC approach—the validation of which is discussed next—enables uncertainty quantification of such collective and reaction observables if the probability distributions for the LECs are available.

Validation of the symmetry-adapted eigenvector continuation

To validate the SA-EVC approach, we show that for the quadrupole moments of the ⁶Li 1⁺ ground state and first excited 3⁺ state, as well as for the 3⁺ excitation energy, the emulators provide very accurate results compared to the exact outcomes (Figure 5). The average relative errors over all 256 validation LECs sets are respectively 6.91 × 10⁻², 7.70 × 10⁻⁴, and 1.20 × 10⁻⁴. It is clear that any deviations of the emulators from the expected values are negligible, especially considering that, as mentioned above, the SA selection reduces the Hamiltonian dimension by more than 97%, and the EVC projection by an additional 99% or more.

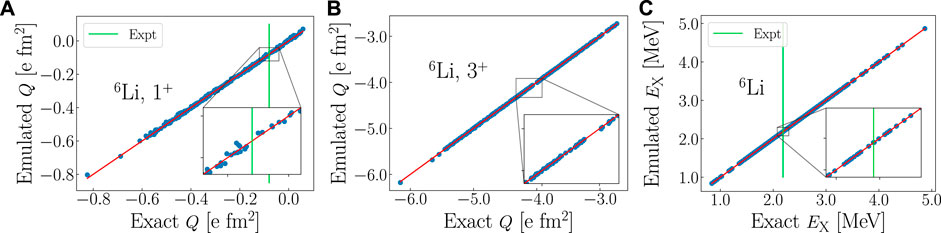
FIGURE 5. Exact vs. SA-EVC observables in ⁶Li (blue circles) for the quadrupole moment Q of (A) the 1⁺ ground state and (B) the first excited 3⁺ state, as well as (C) for the excitation energy E_X of the 3⁺ state, in ⟨2_All⟩8₁₃ SA model spaces and for ℏΩ = 15 MeV. Also shown is the agreement between the exact and emulated values to guide the eye (red line), and experimental results (vertical green line) where available. Insets show 5%-regions surrounding reported experimental data [45] or the NNLO_opt result where data is not available [a 50%-region is used for the very small Q in (A)].

It is worth noting that the average error for the ground state quadrupole moment is two orders of magnitude larger than that of the 3⁺ state. We note that Q(1⁺) of ⁶Li is very similar in nature to the deuteron quadrupole moment. The extremely small value in both nuclei results from a small mixing of an L = 2 component into the ground state of ⁶Li (and of the deuteron), which is not collective in essence like, e.g., the quadrupole moments of the 3⁺ state in ⁶Li or the 2⁺ state in ¹²C (discussed below). Indeed, the results of Figure 5A reflect the high sensitivity of the underlying NN interaction (and likely 3N forces [46]) to the L = 2 mixing in the ground state wave function.

Similar to ⁶Li, the SA-EVC emulated $2_1^{+}$ quadrupole moment and excitation energy for ¹²C are in very close agreement to the exact results (Figure 6). Namely, the average relative errors are given by 1.02 × 10⁻⁴ and 6.72 × 10⁻⁵, respectively. Compared to the average errors reported above for the $3_1^{+}$ quadrupole moment and excitation energy for ⁶Li, we find eight and two times improvement in the emulator’s predictions for ¹²C, respectively. The reason is likely related to the much smaller SA selection in ¹²C and the stronger collective nature observed in the low-lying states of ¹²C. Specifically, in ⁶Li the SA-EVC uses thousands of basis states, whereas in ¹²C only hundreds of basis states (see Table 1). We therefore expect the mixing of configurations to exert a more noticeable effect on ⁶Li than on ¹²C. The result is that the eigenvectors of ¹²C vary in fewer directions than those of ⁶Li, suggesting that more training points for ⁶Li may be beneficial to improve errors. While this warrants further study, this speaks to an advantage of merging the SA and EVC frameworks.

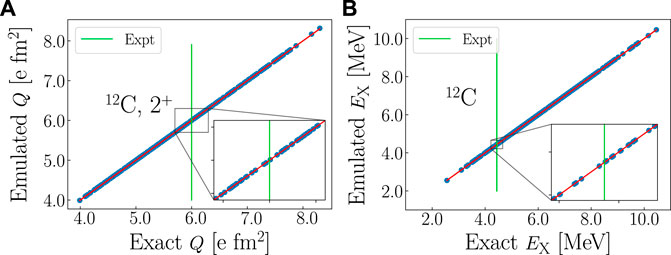
FIGURE 6. The same as in Figure 5 but for (A) the quadrupole moment Q and (B) the excitation energy of the first 2⁺ state in ¹²C, calculated in 6₃ SA model spaces and for ℏΩ = 15 MeV. Insets show 5%-regions surrounding reported experimental data [47].

Conclusion

We have for the first time combined the framework of the SA-NCSM with the EVC procedure into the SA-EVC method for studies of collective and clustering observables. This builds upon earlier SA-NCSM explorations that have shown that an Sp(3,$\mathbb{R}$)-adapted model space selection can successfully capture nuclear collectivity while significantly reducing the sizes of Hamiltonian matrices [8]. Here, we show that excitation energies, point-proton rms radii, electric quadrupole moments and E2 transitions in the two lowest-lying states of ⁶Li and ¹²C calculated with the specific parameterization NNLO_opt for ℏΩ = 15 MeV in SA model spaces are in reasonable agreement with those calculated in the corresponding N_max complete model space (or equally, to NCSM outcomes). We also show that these observables are converged with N_max for the SA selections under consideration.

Further, we demonstrate that SA-EVC emulators trained on SA model spaces are capable of accurately predicting such observables as the LECs are varied, while further reducing the dimensions of operator matrices by an additional 2-3 orders of magnitude. Combined with the initial reduction provided by the SA-NCSM, the emulator matrices have a dimension as much as 10^–5 times smaller than the corresponding N_max complete model spaces. They are small enough to perform linear algebra operations using a single CPU thread on a standard laptop without difficulty. Moreover, the SA-EVC approach will be critical for nuclei beyond the lightest systems; thus, e.g. in ²⁰Ne, the complete N_max = 8 model space has dimension of 1.52 × 10¹¹, while the ab initio SA-NCSM solutions are achieved when using 112 million basis states for J^π = 0⁺, 2⁺, 4⁺. This can be further reduced to emulators of dimension 10² especially given the predominance of a single symplectic irrep in the ground-state rotational band of this nucleus. Comparing the emulator results to exact calculations performed in the same SA spaces, we find that the average relative errors are typically 10^–4. A larger error $(\sim 10^{-2})$ is found for the quadrupole moment of the ⁶Li ground state, which is highly sensitive to the L = 2 admixture and hence to the underlying nuclear force, as discussed in the text. A future study that utilizes larger training sets may provide further insight.

In addition to validating the SA-EVC procedure, we show that the symmetry patterns and clustering features in the emulator training wave functions do not respond strongly to variations in the LECs. Across all of the training wave functions, there is a single nuclear shape (approximate symplectic symmetry) that accounts for 81%–94% of the total probability. Furthermore, the dominance of important SU(3) configurations is preserved from one training wave function to another. Projecting the training wave functions for ⁶Li onto the α + d system, we find that the likelihood of cluster formation in both the ³S₁- and ³D₃-wave channels is largely unaffected by the choice of LECs. Spectroscopic factors, ANCs and α-widths extracted from the cluster wave functions all vary within relatively narrow ranges around their average values, ranges that track reasonably well with the 10% variation of the LECs. This suggests that the part of the nuclear potential that is independent of the LECs and is practically the same for all chiral potentials (up to the regularization and related cutoffs employed) provides the dominant features of the wave function, such as Sp(3,$\mathbb{R}$) symmetry patterns and clustering formation, while varying the LECs and associated unresolved short-range interactions has an effect on, e.g., collective quadrupole moments, asymptotic normalization coefficients (ANCs), and alpha partial widths up to a factor of two.

In order to better understand the relationships between collectivity and clustering explored in this study, and how both relate to the underlying nuclear forces, sensitivity analyses are required. As we enter the era of high-precision nuclear physics, this is also an important step towards constructing accurate interactions, with quantified uncertainties. We note that properly accounting for clustering features is important for the ab initio modeling of nuclear reactions, and related processes from fusion to fission. The SA-EVC method provides a clear and now verified framework for generating the huge number of chiral parameterizations required for such analyses. Hence, the door is now open to perform ab initio calculations with quantified uncertainties that emerge from the interaction and the controlled many-body approximations, from exotic light nuclei up to medium-mass isotopes, as well from spherical to highly enhanced collective and clustering modes.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

We acknowledge invaluable discussions with Jerry P. Draayer, George Rosensteel, David Rowe, and Daniel Langr. This work was supported in part by the U.S. National Science Foundation (PHY-1913728, PHY-2209060), the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant agreement No. 758027), the Czech Science Foundation (22-14497S). KSB greatly appreciates the financial support of a research fellowship from the Louisiana Board of Regents. This work benefited from high performance computational resources provided by LSU (www.hpc.lsu.edu), the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract Nos. DE-AC02-05CH11231, as well as the Frontera computing project at the Texas Advanced Computing Center, made possible by National Science Foundation award OAC-1818253.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Throughout the paper, we will refer to the selected SA-NCSM model spaces as SA model spaces.

²We follow the notations of Ref. [15].

References