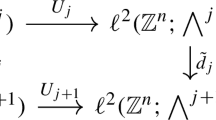Abstract
We consider the quantum graph Hamiltonian on the square lattice in Euclidean space, and we show that the spectrum of the Hamiltonian converges to the corresponding Schrödinger operator on the Euclidean space in the continuum limit, and that the corresponding eigenfunctions and eigenprojections also converge in some sense. We employ the discrete Schrödinger operator as the intermediate operator, and we use a recent result by the second and third authors on the continuum limit of the discrete Schrödinger operator.
Similar content being viewed by others
Data availability
There are no data associated with the this manuscript.
References
Allaire, G., Piatnitski, A.: Homogenization of the Schrödinger equation and effective mass theorems. Commun. Math. Phys. 258(1), 1–22 (2005)
Bakhvalov, N., Panasenko, G.: Homogenisation: Averaging Process in Periodic Media Mathematical Problems in Mechanics of Composite Materials. Mathematics and its Applications (Soviet Series), vol. 36. Kluwer, Dordrecht (1989)
Birman, Sh., Suslina, T.A.: Homogenization with corrector for periodic differential operators. Approximation of solutions in the Sobolev class \(H^1({\mathbb{R}}^d)\). Algebra i Analiz 18(6), 1–130 (2006)
Lovász, L.: Large Networks and Graph Limits, Colloquium Publication, vol. 60. American Mathematical Society, Providence, R.I. (2012)
Berkolaiko, G., Kuchment, P.: Introduction to Quantum Graphs, Matematical Surveys and Monographs, vol. 186. American Mathematical Society, Providence, R.I. (2013)
Exner, P., Hejc̆ík, P., S̆eba, P.: Approximation by graphs and emergence of global structures. Rep. Math. Phys. 57(3), 445–455 (2006)
Nakamura, S., Tadano, Y.: On a continuum limit of discrete Schrödinger operators on square lattice. J. Spectr. Theory 11(1), 355–367 (2021)
Cattaneo, C.: The spectrum of the continuous Laplacian on a graph. Monatsh. Math. 124(3), 215–235 (1997)
Exner, P.: A duality between Schrödinger operators on graphs and certain Jacobi matrices. Ann. Inst. H. Poincaré, Phys. Théor. 66(4), 359–371 (1997)
Pankrashkin, K.: Unitary dimension reduction for a class of self-adjoint extensions with applications to graph-like structures. J. Math. Anal. Appl. 396(2), 640–655 (2012)
Kuchment, P., Post, O.: On the spectra of carbon nano-structures. Commun. Math. Phys. 275(3), 805–826 (2007)
Post, O.: Spectral Analysis on Graph-Like Spaces. Lecture Notes in Mathematics, vol. 2039. Springer, Berlin (2011)
Exner, P., Post, O.: A general approximation of quantum graph vertex couplings by scaled Schrödinger operators on thin branched manifolds. Commun. Math. Phys. 322(1), 207–227 (2013)
Post, O., Simmer, J.: Graph-like spaces approximated by discrete graphs and applications. Math. Nachr. 294(11), 2237–2278 (2021)
Demuth, M., Krishna, M.: Determining Spectra in Quantum Theory. Birkhäuser, Boston (2005)
Simon, B.: Functional Integration in Quantum Physics, 2nd edn. AMS Chelsea, Providence, R.I. (2005)
Cornean, H., Garde, H., Jensen, A.: Norm resolvent convergence of discretized Fourier multipliers. J. Fourier Anal. Appl. 27(4), 71 (2021)
Isozaki, H., Jensen, A.: Continuum limit for lattice Schrödinger operators. Rev. Math. Phys. 34, 2250001 (2022)
Acknowledgements
P.E. was supported by the Czech Science Foundation within the project 21-07129S and by the EU project \(\mathrm{CZ}.02.1.01/0.0/0.0/16_019/0000778\). S.N. was partially supported by JSPS Grant Numbers 15H03622 (2015–2019) and 21K03276 (2021–2024). Y.T. was partially supported by JSPS Grant Numbers 20J00247 (2020–2021) and 21K20337 (2021–2023). This work was supported by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University. The authors appreciate useful comments made by the referees. In particular, Appendix A is added following one of their suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Proof of Corollary 2.4
Appendix A. Proof of Corollary 2.4
Proof of Corollary 2.4
Since we already have
(see [7]), it suffices to show
We note that Corollary 4.3 implies
In fact, by Corollary 4.3, we immediately have
Hence, we have
Let \(z\in {\mathbb {C}}\setminus {\mathbb {R}}\). We note that \((\nu H_1-z)^{-1}\) is bounded from \({\mathcal {H}}_1\) to \(H^1(\Gamma )\), uniformly in \(\ell \). By (A.2), we have
This implies
Then, we consider
but the right-hand side is bounded by \(C{\ell }\) as well as the above argument, simply by replacing z by \({\bar{z}}\), and \(I\varphi \) by \(\varphi \). Thus, we have
Combining this with Theorem 4.6, we have
where \(0<\ell \le 1\).
Let \(R>0\), fixed. We consider the resolvents at \(z=\mu +i\), \(\mu \in [-R,R]\). Here we show the estimate (A.3) holds uniformly in such z. By the resolvent equation, we know
in general, where A is a self-adjoint operator. Let \(\varepsilon >0\), and let \(\{\mu _j\}_{j=1}^N =\{n\varepsilon /3\in [-R,R]\mid n\in {\mathbb {Z}}\}\). We choose \(\ell _0>0\) so small that
for \(0<\ell \le \ell _0\) and \(j=1,\dots , N\). Then, by the \(\varepsilon /3\)-argument, we learn
for all \(\mu \in [-R,R]\), \(0<\ell \le \ell _0\), and this proves the uniform bound.
We now prove the local convergence of the spectrum with respect to the Hausdorff distance. We fix \(R>0\), and consider \(\sigma (\nu H_1)\) and \(\sigma (H_2)\) in \([-R,R]\). Let \(\varepsilon >0\) and we set
We note, for each \(\mu \in \rho _\varepsilon \),
We choose \(\ell _0>0\) so small that
for \(\mu \in [-R,R]\) and \(0<\ell \le \ell _0\). Then, this implies
if \(\mu \in \rho _\varepsilon \) and \(0<\ell \le \ell _0\), and hence, \((\mu -\varepsilon /2,\mu +\varepsilon /2)\subset \rho (H_2)\). In particular, \(\mu \in \rho (H_2)\) if \(\mu \in \rho _\varepsilon \), i.e., \(\rho _\varepsilon \subset \rho (H_2)\), provided \(0<\ell \le \ell _0\). This, in turn, implies \(\sigma (H_2)\cap [-R,R]\) is included in the \(\varepsilon \)-neighborhood of \(\sigma (\nu H_1)\).
Replacing \(\nu H_1\) and \(H_2\), we also learn \(\sigma (\nu H_1)\cap [-R,R]\) is included in the \(\varepsilon \)-neighborhood of \(\sigma (H_2)\) if \(\ell \) is sufficiently small. In other words, we now have
if \(\ell >0\) is sufficiently small. This local convergence implies (A.1) by the spectrum mapping theorem. This completes the proof.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Exner, P., Nakamura, S. & Tadano, Y. Continuum limit of the lattice quantum graph Hamiltonian. Lett Math Phys 112, 83 (2022). https://doi.org/10.1007/s11005-022-01576-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-022-01576-5