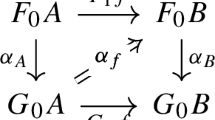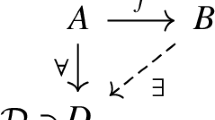Skip to main content
SpringerLink
Log in

General Facts on the Scott Adjunction

  • Published:
Applied Categorical Structures Aims and scope Submit manuscript

Abstract

We introduce, comment and develop the Scott adjunction, mostly from the point of view of a category theorist. Besides its technical and conceptual aspects, in a nutshell we provide a categorification of the Scott topology over a posets with directed suprema. From a technical point of view we establish an adjunction between accessible categories with directed colimits and Grothendieck topoi. We show that the bicategory of topoi is enriched over the 2-category of accessible categories with directed colimits and it has tensors with respect to this enrichment. The Scott adjunction (re-)emerges naturally from this observation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availibility

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

Notes

  1. This is shown in Remark 2.7.

  2. Apply the dual of [7, Thm. 3.3.4] in combination with [8, Thm 1.58].

  3. This will be shown in the remark below.

  4. The free completions that adds splittings of pseudo-idempotents.

  5. These are those limits can be reduced to products, inserters and equifiers.

  6. i.e., send filtered colimits in \(\mathscr {A}\) or \(\mathscr {B}\) to limits in \(\mathbf{Set}\).

  7. Here we are using that \(\mathscr {A}\) and \(\mathscr {B}\) are accessible in order to cut down the size of the orthogonality.

  8. This is not strictly true, because the definition of monoidal closed category does not allow for equivalence of categories. We did not find a precise terminology in the literature and we felt non-useful to introduce a new concept for such a small discrepancy.

  9. This is not quite true, we know that e is a subquotient of \(f^*(g)\), in the general case the proof gets a bit messier to follow, for this reason we will cover in detail just this case.

References

  1. Abramsky, S., Jung, A.: Domain Theory. Claendon Press, Oxford (1994)

    Google Scholar 

  2. Vickers, S.: Locales and Toposes as Spaces, pp. 429–496. Springer, Dordrecht (2007)

    Google Scholar 

  3. Di Liberti, I.: Towards higher topology. J. Pure Appl. Algebra 226(3), 106838 (2022)

    Article  MathSciNet  Google Scholar 

  4. Di Liberti, I.: Formal Model Theory and Higher Topology. arXiv:2010.00319 (2020)

  5. Henry, S.: An abstract elementary class non axiomatizable in \({L_{\infty ,\kappa }}\). J. Symb. Log. 84(3), 1240–1251 (2019)

    Article  MathSciNet  Google Scholar 

  6. Borceux, F.: Handbook of Categorical Algebra. Encyclopedia of Mathematics and its Applications, vol. 3. Cambridge University Press, Cambridge (1994)

    Book  Google Scholar 

  7. Borceux, F.: Handbook of Categorical Algebra. Encyclopedia of Mathematics and its Applications, vol. 1. Cambridge University Press, Cambridge (1994)

    Book  Google Scholar 

  8. Adámek, J., Rosický, J.: Locally Presentable and Accessible Categories. London Mathematical Society Lecture Note Series, vol. 189. Cambridge University Press, Cambridge (1994)

  9. MacLane, S., Moerdijk, I.: Sheaves in Geometry and Logic. Springer, New York (1994)

    Book  Google Scholar 

  10. Johnstone, P.T.: Sketches of an Elephant: A Topos Theory Compendium: 2 Volume Set. Oxford University Press, Oxford (2002)

    MATH  Google Scholar 

  11. Anel, M., Lejay, D.: Exponentiable higher toposes (2018)

  12. Karazeris, P.: Categorical domain theory: Scott topology, powercategories, coherent categories. Theory Appl. Categ. 9, 106–120 (2001). (electronic only)

    MathSciNet  MATH  Google Scholar 

  13. Porst, H.E., Tholen, W.: Concrete dualities. Category theory at work, Herrlich and Porst eds, pp. 11–136. Heldermann-Verlag (1991)

  14. Makkai, M., Pitts, A.M.: Some results on locally finitely presentable categories. Trans. Am. Math. Soc. 299(2), 473–496 (1987)

    Article  MathSciNet  Google Scholar 

  15. Makkai, M.: Strong conceptual completeness for first-order logic. Ann. Pure Appl. Log. 40(2), 167–215 (1988)

    Article  MathSciNet  Google Scholar 

  16. Caramello, O.: The unification of mathematics via topos theory. arXiv preprint arXiv:1006.3930 (2010)

  17. Johnstone, P.T.: Sketches of an Elephant: A Topos Theory Compendium 1: Volume Set. Oxford University Press, Oxford (2002)

    MATH  Google Scholar 

  18. Johnstone, P., Joyal, A.: Continuous categories and exponentiable toposes. J. Pure Appl. Algebra 25(3), 255–296 (1982)

    Article  MathSciNet  Google Scholar 

  19. Beke, T.: Theories of presheaf type. J. Symb. Log. 69(3), 923–934 (2004)

    Article  MathSciNet  Google Scholar 

  20. Espíndola, C.: Infinitary first-order categorical logic. Ann. Pure Appl. Log. 170(2), 137–162 (2019)

    Article  MathSciNet  Google Scholar 

  21. Kelly, G.M., Lawvere, F.W.: On the Complete Lattice of Essential Localizations. Department of Pure Mathematics, University of Sydney, Sydney (1989)

    MATH  Google Scholar 

  22. Makkai, M., Paré, R.: Accessible Categories: The Foundations of Categorical Model Theory. American Mathematical Society, Providence (1989)

    Book  Google Scholar 

  23. Paré, R., Rosický, J.: Colimits of accessible categories. Math. Proc. Camb. Philos. Soc. 155(1), 47–50 (2013)

    Article  MathSciNet  Google Scholar 

  24. Lieberman, M., Rosický, J.: Limits of abstract elementary classes. Theory Appl. Categ. 30(48), 1647–1658 (2015)

    MathSciNet  MATH  Google Scholar 

  25. Kelly, G.M.: Basic Concepts of Enriched Category Theory, vol. 64. Cambridge University Press, Cambridge (1982)

    MATH  Google Scholar 

  26. Di Liberti, I.: The symmetric monoidal closed structure on the category of \(\cal{F}\)-cocomplete categories and \(\cal{F}\)-cocontinuous functors. MathOverflow. https://mathoverflow.net/users/104432/ivan-di liberti. https://mathoverflow.net/q/350869 (version: 2020-01-21)

  27. Bourke, J.: Skew structures in 2-category theory and homotopy theory. J. Homotopy Relat. Struct. 12(1), 31–81 (2017)

    Article  MathSciNet  Google Scholar 

  28. Hyland, M., Power, J.: Pseudo-commutative monads and pseudo-closed 2-categories. J. Pure Appl. Algebra 175(1), 141–185 (2002). Special Volume celebrating the 70th birthday of Professor Max Kelly

  29. Franco, I.L.: Pseudo-commutativity of KZ 2-monads. Adv. Math. 228(5), 2557–2605 (2011)

    Article  MathSciNet  Google Scholar 

  30. Adámek, J., Rosický, J.: How nice are free completions of categories? Top. Appl. 273, 106972 (2020)

    Article  MathSciNet  Google Scholar 

  31. Brandenburg, M.: Tensor categorical foundations of algebraic geometry. arXiv preprint arXiv:1410.1716 (2014)

  32. Lurie, J.: Higher Topos Theory (AM-170). Princeton University Press, Princeton (2009)

    Book  Google Scholar 

  33. Garner, R., Shulman, M.: Enriched categories as a free cocompletion. Adv. Math. 289, 1–94 (2016)

    Article  MathSciNet  Google Scholar 

  34. Pitts, A.: On product and change of base for toposes. Cahiers de topologie et géométrie différentielle catégoriques 26(1), 43–61 (1985)

    MathSciNet  MATH  Google Scholar 

  35. Adámek, J., El Bashir, R., Sobral, M., Velebil, J.: On functors which are lax epimorphisms. Theory Appl. Categ. 8, 509–521 (2001)

    MathSciNet  MATH  Google Scholar 

  36. Lieberman, M., Rosickỳ, J., Vasey, S.: Hilbert spaces and C-algebras are not finitely concrete. arXiv preprint arXiv:1908.10200 (2019)

Download references

Acknowledgements

I am indebted to my advisor, Jiří Rosický, for the freedom and the trust he blessed me with during these years, not to mention his sharp and remarkably blunt wisdom. I would like to thank Simon Henry, for his collaboration in those days in which this project was nothing but an informal conversation at the whiteboard. I am grateful to Peter Arndt, for his sincere interest in my research, and the hint of looking at the example of the geometric theory of fields. Finally, I am grateful to the anonymous referee for their suggestions and comments.

Author information

Authors and Affiliations

  1. Institute of Mathematics, Czech Academy of Sciences, Žitná 25, Prague, Czech Republic

    Ivan Di Liberti

Authors
  1. Ivan Di Liberti
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This research was mostly developed during the Ph.D. studies of the author and has been supported through the Grant 19-00902S from the Grant Agency of the Czech Republic. The finalization of this research has been supported by the GACR Project EXPRO 20-31529X and RVO: 67985840.

Communicated by Thomas Streicher.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Di Liberti, I. General Facts on the Scott Adjunction. Appl Categor Struct 30, 569–591 (2022). https://doi.org/10.1007/s10485-021-09666-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10485-021-09666-6

Keywords

Search

Navigation