Online Scheduling of Jobs with Fixed Start Times on Related Machines

Abstract

We consider online preemptive scheduling of jobs with fixed starting times revealed at those times on $m$ uniformly related machines, with the goal of maximizing the total weight of completed jobs. Every job has a size and a weight associated with it. A newly released job must be either assigned to start running immediately on a machine or otherwise it is dropped. It is also possible to drop an already scheduled job, but only completed jobs contribute their weights to the profit of the algorithm. In the most general setting, no algorithm has bounded competitive ratio, and we consider a number of standard variants. We give a full classification of the variants into cases which admit constant competitive ratio (weighted and unweighted unit jobs, and C-benevolent instances, which is a wide class of instances containing proportional-weight jobs), and cases which admit only a linear competitive ratio (unweighted jobs and D-benevolent instances). In particular, we give a lower bound of $m$ on the competitive ratio for scheduling unit weight jobs with varying sizes, which is tight. For unit size and weight we show that a natural greedy algorithm is $4/3$-competitive and optimal on $m=2$ machines, while for large $m$, its competitive ratio is between $1.56$ and $2$. Furthermore, no algorithm is better than $1.5$-competitive.

1 Introduction

Scheduling jobs with fixed start times to maximize (weighted) throughput is a well-studied problem with many applications, for instance work planning for personnel, call control and bandwidth allocation in communication channels [1, 3]. In this paper, we consider this problem for uniformly related machines. Jobs with fixed starting times are released online to be scheduled on $m$ machines. Each job needs to start immediately or else be rejected. The completion time of a job is determined by its length and the speed of a machine. As pointed out by Krumke et al. [13], who were the first to study them for uniformly related machines, problems like these occur when jobs or material should be processed immediately upon release, but there are different machines available for processing, for instance in a large factory where machines of different generations are used side by side. Because on identical machines, the size of the job together with its fixed start time determine the time interval that one of the machines has to devote to the job in order to complete it, this problem is commonly known as interval scheduling [6–10]. In fact, Krumke et al. [13] used the name interval scheduling on related machines, but we refrain from it as different speeds translate into different time intervals for different machines, albeit with a common start time.

We consider the preemptive version of this problem, where jobs can be preempted (and hence lost) at any time (for example, if more valuable jobs are released later). Without preemption, it is easy to see that no online algorithm can be competitive for most models. The only exception is the simplest version of this problem, where all jobs have unit size and weight. For this case, preemption is not needed.

1.1 Our Results

It is known (cf. Sect. 1.3) that if both the weight and the size of a job are arbitrary, then no (randomized) algorithm is competitive on identical machines, a special case of related machines. Therefore, we study several restricted models.

One of them is the case of jobs with unit sizes and unit weights, studied in Sect. 2. While a trivial greedy algorithm is 1-competitive in this case on identical machines (cf. Sect. 1.3), attaining this ratio on related machines is impossible. We give a lower bound of $(3\cdot 2^{m-1}-2)/(2^m-1)$ on the competitive ratio for this case, which for large $m$ tends to $3/2$ from below. The high level reason why this holds is that the optimal assignment of jobs to machines may depend on the timing of future arrivals. We also show that a simple greedy algorithm is $2$-competitive and we use a more complicated lower bound construction to show that it is not better than $1.56$-competitive for large $m$. For $m=2$ machines, we show that it is $4/3$-competitive, matching the lower bound.

Next, in Sect. 3, we consider two extensions of this model: weighted jobs of unit sizes and a model where the weight of a job is determined by a fixed function of its size, $f:\mathbb {R}^{+}_{0}\rightarrow \mathbb {R}^{+}_{0}$ (where $\mathbb {R}^{+}_{0}$ denotes the non-negative reals).

A function is C-benevolent if it is convex, $f(0)=0$, and $f(p)>0$ for all $p>0$. This includes the important case of proportional weights given by $f(x)=ax$ for some $a>0$. The property that a function is $C$-benevolent implies in particular that $f$ is continuous in $(0,\infty )$, and monotonically non-decreasing. We consider instances, called C-benevolent instances, where the weights of jobs are given by a fixed C-benevolent function $f$ of their sizes, that is, $w(j)=f\left( (p(j)\right)$. We call such an instance $f$-benevolent.

We give a $4$-competitive algorithm, which can be used both for $f$-benevolent instances and for weighted unit-sized jobs. This generalizes the results of Woeginger [15] for these models on a single machine; cf. Sect. 1.3.

Finally, in Sect. 4, we give a lower bound of $m$ for unit-weight variable-sized jobs, which is tight due to a trivial 1-competitive algorithm for a single machine [4, 6] and the following simple observation.

Fact 1.1

If algorithm ${\textsc {Alg}}$ is $R$-competitive on a single machine, then an algorithm that uses only the fastest machine by simulating ${\textsc {Alg}}$ on it is $(R \cdot m)$-competitive on $m$ related machines.

Proof

Fix an instance and the optimum schedule for it on $m$ related machines. To prove our claim, it suffices to show that a subset of jobs from that schedule with total weight no smaller than a $1/m$ fraction of the whole schedule’s weight can be scheduled on the fastest machine. Clearly, one of the machines is assigned a subset of sufficient weight in the optimum schedule, and this set can be scheduled on the fastest machine. $\square$

Instances with unit-weight variable-sized jobs are a special case of D-benevolent instances: a function $f$ is D-benevolent if it is decreasing on $(0,\infty )$, $f(0)=0$, and $f(p)>0$ for all $p>0$. (Hence such functions have a discontinuity at 0.) Hence our lower bound of $m$ applies to D-benevolent instances as well, and again we obtain an optimal (up to a constant factor) algorithm by combining a 4-competitive algorithm for a single machine [15] with Fact 1.1. Note that in contrast, C-benevolent functions are not a generalization of unit weights and variable sizes, because the constraint $f(0)=0$ together with convexity implies that $f(cx)\ge c\cdot f(x)$ for all $c>0,x>0$, so the weight is at least a linear function of the size.

We give an overview of our results and the known results in Table 1. In this table, a lower bound for a class of functions means that there exists at least one function in the class for which the lower bound holds.

Table 1 An overview of old and new results for deterministic algorithms; upper bounds by randomized algorithms (UBr) are also given for a single machine

1.2 Notation

There are $m$ machines, $M_1,M_2,\ldots ,M_m$, in order of non-increasing speed. Their speeds, all no larger than $1$, are denoted by $s_1 \ge s_2 \ge \cdots \ge s_m$ respectively. We say that machine $i_1$ is faster than machine $i_2$ if $i_1 < i_2$ (even if $s_{i_1}=s_{i_2}$). For an instance $I$ and algorithm Alg, ${\textsc {Alg}}(I)$ and ${\textsc {Opt}}(I)$ denote the total weight of jobs completed by Alg and an optimal schedule, respectively. The algorithm is $R$-competitive if ${\textsc {Opt}}(I)\le R\cdot {\textsc {Alg}}(I)$ for every instance $I$.

For a job $j$, we denote its size by $p(j)$, its release time by $r(j)$, and its weight by $w(j)>0$. Any job that an algorithm runs is executed in a half-open interval $[r,d)$, where $r=r(j)$ and $d$ is the time at which the job completes or is preempted. We call such intervals job intervals. If a job (or a part of a job) of size $p$ is run on machine $M_i$ then $d=r+\frac{p}{s_i}$. A machine is called idle if it is not running any job, otherwise it is busy.

1.3 Previous Work

As mentioned before, if both the weight and the size of a job are arbitrary, then no (randomized) algorithm is competitive, either on one machine [3, 15] or identical machines [3]. For completeness, we formally extend this result to any set of related machines and show that for the most general setting, no competitive algorithm can exist (not even a randomized one).

Proposition 1.2

For any set of $m$ machine speeds, the competitive ratio of every randomized algorithm for variable lengths and variable weights is unbounded.

Proof

Let ${\textsc {Alg}}_m$ be an arbitrary randomized preemptive algorithm for $m$ machines of speeds $s_1,\ldots ,s_m$. Recall that $s_1=\max _{1 \le i \le m} s_i$. Let $C$ be an arbitrary constant, and let $C'=mC$. Define the following algorithm ${\textsc {Alg}}$ for one machine of speed $s_1$: ${\textsc {Alg}}$ chooses an integer $i$ in $\{1,2,\ldots ,m$} uniformly with probability $1/m$ and acts as ${\textsc {Alg}}_m$ acts on machine $i$. Since the speed of $i$ is at most $s_1$, this is possible. Note that ${\textsc {Alg}}$ is randomized even if ${\textsc {Alg}}_m$ is deterministic. For every input $J$, $\mathbb E({\textsc {Alg}}(J))=\frac{1}{m}\cdot \mathbb E({\textsc {Alg}}_m(J))$.

Let ${\textsc {Opt}}_m$ denote an optimal solution for $m$ machines, and ${\textsc {Opt}}_1$ on one machine. Clearly ${\textsc {Opt}}_1(J)\le {\textsc {Opt}}_m(J)$ for every input $J$. Let $I$ be an input such that ${\textsc {Opt}}_1(I)\ge C' \cdot \mathbb E({\textsc {Alg}}(I))$ (its existence is guaranteed, since Alg’s competitive ratio is unbounded [3]). Then $C \cdot \mathbb E({\textsc {Alg}}_m(I)) = m C \cdot \mathbb E({\textsc {Alg}}(I)) \le {\textsc {Opt}}_1(I) \le {\textsc {Opt}}_m(I)$. Thus the competitive ratio of ${\textsc {Alg}}_m$ is unbounded. $\square$

For this general case on one machine, it is possible to give an $O(1)$-competitive algorithm, and even a $1$-competitive algorithm, using constant resource augmentation on the speed; that is, the machine of the online algorithm is $O(1)$ times faster than the machine of the offline algorithm that it is compared to [11, 12].

Baruah et al. [2] considered online scheduling with deadlines, including the special case (zero laxity) of interval scheduling. They focused on the proportional weight case and gave a 4-competitive algorithm for a single machine and a 2-competitive algorithm for two identical machines. Woeginger [15] considered interval scheduling on a single machine and gave a 4-competitive algorithm for unit sized jobs with weights, C-benevolent jobs, and D-benevolent jobs. He also showed that this algorithm is optimal for the first two settings.

Faigle and Nawijn [6] and Carlisle and Lloyd [4] considered the version of jobs with unit weights on $m$ identical machines. They gave a 1-competitive algorithm for this problem.

For unit sized jobs with weights, Fung et al. [9] gave a 3.59-competitive randomized algorithm for one and two (identical) machines, as well as a deterministic lower bound of $2$ for two identical machines. The upper bound for one machine was improved to 2 by the same authors [8] and later generalized to the other nontrivial models [10].¹ See [5, 14] for additional earlier randomized algorithms. A randomized lower bound of 1.693 for one machine was given by Epstein and Levin [5]; Fung et al. [7] pointed out that it holds for parallel machines as well, and gave an upper bound for that setting (not shown in the table): a 2-competitive algorithm for even $m$ and a $(2+2/(2m-1))$-competitive algorithm for odd $m\ge 3$.

2 Unit Sizes and Weights

In this section we consider the case of equal jobs, i.e., all the weights are equal to $1$ and also the size of each job is $1$. We first note that it is easy to design a 2-competitive algorithm, and for 2 machines we find an upper bound of $4/3$ for a natural greedy algorithm.

The main results of this section are the lower bounds. First we prove that no online algorithm on $m$ machines can be better than $(3\cdot 2^{m-1} -2)/(2^m -1)$-competitive. This matches the upper bound of $4/3$ for $m=2$ and tends to $1.5$ from below for $m\rightarrow \infty$. For Greedy on $m=3n$ machines we show a larger lower bound of $(25\cdot 2^{n-2}-6)/(2^{n+2}-3)$, which tends to $25/16=1.5625$ from below. Thus, somewhat surprisingly, Greedy is not $1.5$-competitive.

2.1 Greedy Algorithms and Upper Bounds

As noted in the introduction, in this case preemptions are not necessary. We may furthermore assume that whenever a job arrives and there is an idle machine, the job is assigned to some idle machine. We call such an algorithm greedy-like.

Fact 2.1

Every greedy-like algorithm is $2$-competitive.

Proof

Let Alg be a greedy-like algorithm. Consider the following charging from the optimum schedule to Alg’s schedule. Upon arrival of a job $j$ that is in the optimum schedule, charge $j$ to itself in Alg’s schedule if Alg completes $j$; otherwise charge $j$ to the job Alg is running on the machine where the optimum schedule assigns $j$. As every Alg’s job receives at most one charge of either kind, Alg is 2-competitive. $\square$

We also note that some of these algorithms are indeed no better than $2$-competitive: If there is one machine with speed $1$ and the remaining $m-1$ have speeds no larger than $\frac{1}{m}$, an algorithm that assigns an incoming job to a slow machine whenever possible has competitive ratio no smaller than $2-\frac{1}{m}$. To see this, consider an instance in which $m-1$ successive jobs are released, the $i$-th of them at time $i-1$, followed by $m$ jobs all released at time $m-1$. It is possible to complete them all by assigning the first $m-1$ jobs to the fast machine, and then the remaining $m$ jobs each to a dedicated machine. However, the algorithm in question will not complete any of the first $m-1$ jobs before the remaining $m$ are released, so it will complete exactly $m$ jobs.

Algorithm Greedy: Upon arrival of a new job: If some machine is idle, schedule the job on the fastest idle machine. Otherwise reject it.

While we cannot show that Greedy is better than 2-competitive in general, we think it is a good candidate for such an algorithm. We support this by showing that it is optimal for $m=2$.

Theorem 2.2

Greedy is $4/3$-competitive algorithm for interval scheduling of unit size and weight jobs on 2 related machines.

Proof

Consider a schedule of Greedy and split it into non-overlapping intervals $[R_i,D_i)$ as follows. Let $R_1 \ge 0$ be the first release time. Given $R_i$, let $D_i$ be the first time after $R_i$ when each one of the machines has the property that it is either idle, or it has just started a new job (the case that it just completed a job and did not start a new job is contained in the case that it is idle). Given $D_i$, $R_{i+1}$ is defined if there exists at least one job with a release time in $[D_i,\infty )$. In this case, let $R_{i+1}$ be the first release time that is larger than or equal to $D_i$. If $R_{i+1}>D_i$, then obviously no job is released in the interval $[D_i,R_{i+1})$, and both machines are idle during this time interval. If $D_i=R_{i+1}$, then at least one job is released at time $D_i$, and at least one machine of Greedy starts a new job at this time. By the definition of the values $R_i$ and the algorithm, at least one machine of Greedy (i.e., machine $M_1$) starts a job at time $R_i$, for all values of $i\ge 1$ such that $R_i$ is defined.

We consider an optimal schedule Opt. We will compare the number of jobs started by Greedy and by Opt during one time interval $[R_i,D_i)$. First, we will show that the number of jobs that Opt starts can be larger than the number of jobs that Greedy can start by at most $1$. Next, we will show that if Greedy started one or two jobs, then the number of jobs that Opt started cannot exceed that of Greedy. This will show that during each $[R_i,D_i)$, Opt starts at most $4/3$ times the number of jobs that Greedy does, which will imply the claimed competitive ratio. Thus, in what follows, we discuss a specific time interval $[R_i,D_i)$.

Consider a maximal time interval that a machine $M_{\ell }$ of Greedy is busy. Since all jobs are unit jobs, the number of jobs that Opt starts during this time interval on $M_{\ell }$ does not exceed the number of jobs that Greedy runs on $M_{\ell }$ during this interval. On the other hand, if a machine is idle during a (maximal) time interval $[t_1,t_2)$ (where $t_1<t_2\le D_i$), then no jobs are released during $(t_1,t_2)$, so ${\textsc {Opt}}$ does not start any jobs during $(t_1,t_2)$. If $t_1=R_i$, then $[t_1,t_2)$ must be an interval of idle time on $M_2$ (since $M_1$ is not idle at time $R_i$), and ${\textsc {Opt}}$ possibly starts a job at time $t_1$. If $t_1>R_i$, then we claim that no job is released at time $t_1$. Assume by contradiction that a job $j$ is released at this time. If Greedy does not run $j$, then we get a contradiction, since it has an idle machine at time $t_1$. Thus, it runs $j$ on the other machine, and we find that the time $t_1$ is such that one machine is idle, and the other one just started a job. Thus, by the definition of $R_i$ we get $R_i \le t_1$, a contradiction as well. Thus, Opt can start as most as many jobs as Greedy during the time intervals that both machines of Greedy are running jobs, and it can start at most one job during all intervals that a machine of Greedy is idle.

If Greedy starts only one job in $[R_i,D_i)$, then exactly one job is released at time $R_i$, and no jobs are released during $(R_i,D_i)$, so ${\textsc {Opt}}$ can start at most one job during $[R_i,D_i)$. Consider the case that Greedy starts two jobs in $[R_i,D_i)$. In this case, the first job is started on $M_1$ at time $R_i$. If no job is started on $M_2$ strictly before the time $R_i+\frac{1}{s_1}$, then $D_i=R_i+\frac{1}{s_1}$, contradicting the assumption that a second job is started by Greedy during $[R_i,D_i)$. Since $M_1$ is idle during the time $[R_i+\frac{1}{s_1},D_i)$, no jobs are released during this time interval (this time interval can be empty if $s_1=s_2$ and both jobs are released at time $D_i$). Since $s_1 \ge s_2$, ${\textsc {Opt}}$ cannot start more than one job on each machine during $[R_,R_i+\frac{1}{s_1})$, and thus it starts at most two jobs as well. This completes the proof. $\square$

2.2 Lower Bounds

We give two lower bounds, for any deterministic algorithm ${\textsc {Alg}}$ and for Greedy that, with the number of machines tending to infinity, tend to $3/2$ and $25/16$ respectively from below. In this section we see an offline solution as an adversary. For both constructions, we have $m$ machines with geometrically decreasing speeds (as a function of the indices). The instance has two sets of jobs. The first part, $I_m$, is the set of jobs that both the algorithm and the adversary complete. The other part, $E_m$, consists of jobs that are completed only by the adversary.

Intuitively, the instance $(I_m,E_m)$ for the general lower bound can be described recursively. The set $I_m$ contains $m$ jobs that are called leading that are released in quick succession, so that no two can be assigned to the same machine. The adversary schedules these $m$ jobs on different machines, cyclically shifted, so that one of them finishes later than in Alg but the remaining $m-1$ finish earlier. For each one of these $m-1$ jobs, upon its completion, the adversary releases and schedules a job from $E_m$; the adversary maintains the invariant that at the time of release of any of these jobs from $E_m$, all the machines are busy in the schedule of Alg. To ensure this, the instance $I_m$ also contains $m-1$ subinstances $I_1,\dots ,I_{k-1}$ (which recursively contain further subinstances themselves). Each subinstance $I_i$ is released at a time when $m-i$ of the leading jobs are still running, and its jobs occupy the machines of ${\textsc {Alg}}$ when the job of $E_m$ arrives. The main technical difficulty lies in ensuring this property no matter how ${\textsc {Alg}}$ assigns the leading jobs of $I_m$ or of any subinstance. We need to make the offsets of the leading jobs geometrically decreasing in the nested subinstances, and adjust the timing of the subinstances carefully depending on the actual schedule.

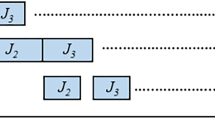
This construction for $k=3$ with $|I_3|=7$ and $|E_3|=3$ as applied to $\textsc {Greedy}$ is illustrated in Fig. 1; the constructions for $k=1,2$ appear as subinstances of a single job ($|I_1|=1$, $E_1=\emptyset$) and of four jobs ($|I_2|=3$, $|E_2|=1$) respectively. For $\textsc {Greedy}$, we of course know in advance how any leading job will be scheduled (on the fastest available machine) and it is straightforward to determine the timing of the subinstances $I_1$ and $I_2$ to ensure that the machines are busy when $e_2$ and $e_3$ arrive. In fact, as we will see below, for $\textsc {Greedy}$ we can slightly improve upon this construction.

Fig. 1

The instance $(I_3,E_3)$ as applied to Greedy. The leading jobs of $I_3$ are gray. Common jobs in Greedy and Adv schedule are joined using dotted lines. Jobs that only Adv completes are thicker. In this figure, for simplicity we have used one common value $\varepsilon _i=\varepsilon$ ($i=1,2,3$). We will argue later that this is sufficient for $\textsc {Greedy}$

Theorem 2.3

Let ${\textsc {Alg}}$ be an online algorithm for interval scheduling of unit size and unit weight jobs on $m$ related machines. Then the competitive ratio of ${\textsc {Alg}}$ is at least $(3\cdot 2^{m-1} -2)/(2^m -1)$.

Proof

Following Sect. 2.1, we may assume that Alg is greedy-like. Let Adv denote the schedule of the adversary which we construct along with the instance.

Fix $m$, the number of machines and the speeds $s_k=4^{-k}$. Thus a job processed on $M_k$ takes time $\frac{1}{s_k}=4^{k}$. Let $\mathcal {M}_k=\{M_1,\ldots ,M_k\}$ denote the set of $k$ fastest machines from $\mathcal {M}$. For $k=1,\ldots ,m$, let $\varepsilon _k=m^{k-m-1}$. Note that $\varepsilon _k<1$ and $k\varepsilon _k<m\varepsilon _k=\varepsilon _{k+1}$ for all $k<m$, while $\varepsilon _m=\frac{1}{m}$. To prove the bound, we are going to inductively construct a sequence of instances $(I_1,E_1)$, $(I_2,E_2)$, ..., $(I_m,E_m)$. Each instance $I_k$ is run by both Alg and Adv on machines $\mathcal {M}_k$.

The precondition for invoking an occurrence of $(I_k,E_k)$ at time $R_k$ is that the machines in $\mathcal {M}\backslash \mathcal {M}_k$ in the schedule of ${\textsc {Alg}}$ are busy with already released jobs throughout the interval $[R_k,R_k+\frac{1}{s_k}+k\varepsilon _k)$, whereas the machines in $\mathcal {M}_k$ are idle starting from time $R_k$ for both $\textsc {Adv}$ and ${\textsc {Alg}}$. All jobs of $(I_k,E_k)$ will be released in $[R_k,R_k+\frac{1}{s_k}+k\varepsilon _k)$.

Now we describe the recursive construction of $I_k$ and $E_k$ together with the schedule of Adv. The construction depends on the actual schedule of Alg before the current time; this is sound, as during the construction the current time only increases. (Note that this also means that different occurrences of $(I_k,E_k)$ may look slightly different.)

The first $k$ jobs of $I_k$ are called its leading jobs and are denoted by $j_1,j_2,\ldots ,j_k$. For $i=1,\dots ,k$, the job $j_i$ is released at time $R_k+i\varepsilon _k < R_k+1$. When the last of these jobs arrives, which is before any of them can finish since $s_i<1$ for $i=1,\ldots ,m$, it is known where ALG assigned each of the jobs and exactly when they will finish. Alg assigns all the leading jobs to machines in $\mathcal {M}_k$ in one-to-one correspondence, since Alg is greedy-like (and we assume the precondition holds). Denote the completion time of the leading job on machine $M_i$ of ${\textsc {Alg}}$ by $C_i$ for $i=1,\dots ,k$.

For $i=1,\ldots ,k-1$, Adv schedules $j_i$ on the machine where Alg schedules $j_{i+1}$; Adv schedules $j_k$ on the machine where Alg schedules $j_1$. Hence, at time $C_{i}+k\varepsilon _k$, $\textsc {Adv}$ still has at most $k-i$ unfinished leading jobs of $I_k$ left, which are running on the slowest machines of $\mathcal {M}_k$.

We have

$$\begin{aligned} C_{i+1}-C_{i}&> 4^{i+1}-4^{i}-k\varepsilon _k > 2\cdot 4^{i}+i\varepsilon _{i} \end{aligned}$$

(1)

$$\begin{aligned}&> k\varepsilon _k, \end{aligned}$$

(2)

using that $i\varepsilon _i<k\varepsilon _k\le 1$ for $1\le i<k\le m$. By (2), there will be exactly $k-1$ disjoint intervals of length $\varepsilon _k$ in $[R_k,R_k+\frac{1}{s_k}+k\varepsilon _k]$ of the form $[C_i-\varepsilon _k,C_i]$ in which ${\textsc {Alg}}$ has one more unfinished leading job than $\textsc {Adv}$. We call these intervals good intervals.

For each $i=1,\ldots ,k-1$ in increasing order, we now do the following. If $[C_{i}-\varepsilon _k,C_{i}]$ is good, release an extra job at time $C_i-\varepsilon _k$. $\textsc {Adv}$ schedules this job on machine $M_i$. Regardless of whether $[C_{i}-\varepsilon _k,C_{i}]$ is good, let

$$\begin{aligned} R_i:=C_{i+1}-\frac{1}{s_{i}}-i\varepsilon _i, \end{aligned}$$

(3)

and construct recursively an occurrence of the instance $(I_i,E_i)$, including Adv schedule, at time $R_i$. Note that the precondition for $(I_k,E_k)$ plus the fact that there are still $k-i$ leading jobs running in the whole interval $[R_i,C_{i+1}]$ (due to 1) implies that the precondition holds for the subinstance $(I_i,E_i)$ as well.

For the rest of the construction and of the proof, let $(I_i,E_i)$ denote this particular occurrence. Denote the set of the $k-1$ extra jobs released in good intervals by $E_0$. Finally, let $I_k=\{j_1,j_2,\ldots ,j_k\}\cup I_1\cup \cdots \cup I_{k-1}$ and $E_k=E_0\cup E_1\cup \cdots \cup E_{k-1}$. This completes the description of $(I_k,E_k)$. $\square$

Claim 2.4

If the precondition holds, both Alg and Adv complete all jobs from $I_k$ on machines $\mathcal {M}_k$ no later than $R_k+\frac{1}{s_k}+k\varepsilon _k$.

Proof

This follows for the leading jobs of $I_k$ since all these jobs are released no later than at time $R_k+k\varepsilon _k$ (and since the $k$ fastest machines are idle for both ${\textsc {Alg}}$ and $\textsc {Adv}$ by the precondition), and for the other jobs from the fact that $(I_i,E_i)$ is released at time $C_{i+1}-\frac{1}{s_{i}}-i\varepsilon _i$, meaning all jobs in $I_i$ complete by time $C_{i+1}$ by induction in both the schedule of ${\textsc {Alg}}$ and $\textsc {Adv}$; in particular, all jobs in $I_{k-1}$ complete by time $C_k \le R_k+\frac{1}{s_k}+k\varepsilon _k$. $\square$

The following claim implies that ${\textsc {Alg}}$ cannot schedule any extra job. Notice that an extra job of $(I_k,E_k)$ is released at time $C_i-\varepsilon _k$ for some $i\le k$.

Claim 2.5

For any occurrence of $(I_k,E_k)$, if the precondition holds at time $R_k$, then for any $i\le k$, at time $C_i-\varepsilon _k$, all machines from $\mathcal {M}$ are busy running jobs in ${\textsc {Alg}}$.

Proof

Consider any $i\le k$. Machines $M_i$, $i>k$ are busy in ${\textsc {Alg}}$ by the precondition. Machines $M_i$, ..., $M_k$ are running the leading jobs of $(I_k,E_k)$ by the construction. We now use induction on $k$ to prove that machines from $\mathcal {M}_{i-1}$ are busy. If $i=1$, this is trivial.

Let $i>1$. The leading job of $(I_{i-1},E_{i-1})$ (i.e., the occurrence of $(I_{i-1},E_{i-1})$ from the construction of $(I_k,E_k)$ released at $R_{i-1}=C_i-\frac{1}{s_{i-1}}-i\varepsilon _{i-1}$) scheduled by ${\textsc {Alg}}$ on $M_{i-1}$ completes at some time $C'\in [C_i-(i-1)\varepsilon _{i-1},C_i]$, by the construction of the leading jobs. By the induction assumption for $(I_{i-1},E_{i-1})$, at time $C'-\varepsilon _{i-1}$ all machines are busy in ${\textsc {Alg}}$. Since the jobs these machines are running are from $(I_{i-1},E_{i-1})$, by Claim 2.4 used for $(I_{i-1},E_{i-1})$ they complete by $C_i$. Thus they must be running already before time $C_i-\varepsilon _k$, as $\varepsilon _k<1$. Since $C'-\varepsilon _{i-1}\ge C_i-i\varepsilon _{i-1}\ge C_i-\varepsilon _k$, they are running also after $C_i-\varepsilon _k$ and thus also at $C_i-\varepsilon _k$. $\square$

The input for the algorithm is now simply one instance of $(I_m,E_m)$; we set $R_m=0$. For this instance, the precondition trivially holds.

As noted above (below (3)), this implies that the precondition also holds for all subinstances $(I_i,E_i)$.

Finally, by Claim 2.5, ${\textsc {Alg}}$ does not run any extra job, while $\textsc {Adv}$ runs all of them since they are released in good intervals. It remains to count the number of jobs in $I_k$ and $E_k$. We claim that $|I_k|=2^{k}-1$ and $|E_k|=2^{k-1}-1$. This is clear for $k=1$, since $|I_1|=1$ and $E_1=\emptyset$. Using the inductive assumption, we get $|I_k|=k+\sum _{i=1}^{k-1}|I_i|=k+\sum _{i=1}^{k-1}(2^i-1)=2^k-1$ and $|E_k|=k-1+\sum _{i=1}^{k-1}|E_i|=k-1+\sum _{i=1}^{k-1}(2^{i-1}-1)=2^{k-1}-1$. Hence the competitive ratio of Alg is at least $\left( (2^{m}-1)+(2^{m-1}-1)\right) /(2^{m}-1)=(3\cdot 2^{m-1} -2)/(2^m -1)$. $\square$

The second lower bound is higher, however it only works for Greedy. We observe that cyclic shift of the leading jobs may not be the best permutation for the adversary. Instead, we create triples of machines of equal speeds (among the three machines of the triple) and shift the jobs cyclically among the triples. That is, the permutation of the leading jobs has three independent cycles of length $m/3$. There is one triple where the speeds are not equal, and this is the set of the three fastest machines for which we use different speeds and the previous construction as a subinstance.

Consider the previous construction $I$ as applied to $\textsc {Greedy}$, as shown for three machines in Fig. 1. We make two changes. The first change is already shown in Fig. 1: since $\textsc {Greedy}$ prefers faster machines, we now set $\varepsilon _i=\varepsilon =\frac{1}{m}$ at every recursive step of the construction. We denote the modified version of $(I_k,E_k)$ by $(I_k',E_k')$ for all $k$. For any instance $(I_i',E_i'$), assuming the precondition (with $\varepsilon _i$ replaced by $\varepsilon$) for time $R_i'$, $\textsc {Greedy}$ assigns leading job $j_i'$ which arrives at time $R_i'+i\varepsilon$ to machine $M_i$. Thus in the construction of $(I_k',E_k')$, as in (3) we let $R_i'=C_{i+1}-i\varepsilon -\frac{1}{s_i}$ and thus ensure that $\textsc {Greedy}$ completes $j_i'$ at exactly the same time as the leading job on machine $M_{i+1}$ in the schedule of $\textsc {Greedy}$ for $(I_k',E_k')$. This defines the input $I'$.

Using the same cyclically shifted assignment as before, the only machine where $\textsc {Adv}$ completes leading jobs later than (or at the same time as) $\textsc {Greedy}$ is $M_1$, on all other machines it completes each leading job $\varepsilon$ time earlier. By induction, it is straightforward to show that when $\textsc {Greedy}$ completes any leading job on some machine $M_i$, it also completes a leading job on machines $M_1,\dots ,M_{i-1}$ at exactly the same time. It follows (also by induction) that $\varepsilon$ time before the leading job of the top-level subinstance $(I_i,E_i)$ completes ($i=1,\dots ,k-1$), all machines of $\textsc {Greedy}$ are busy, whereas $i$ machines of $\textsc {Adv}$ are idle, namely machines $M_2,\dots ,M_{i+1}$.

We now further modify $I'$ as follows. Every machine $M_4,\dots ,M_k$ is replaced by a cluster of three machines of identical speed. E.g., machine $M_4$ of speed $s_4$ is replaced by three machines of speed $s_4$. Every time that one job of $I_k'$ which is scheduled by $\textsc {Greedy}$ on some machine $M_i$, $i>3$ or a job of $E_k'$ arrives which is only scheduled by $\textsc {Adv}$ on some machine $M_i$, $i>3$, we instead let three jobs arrive simultaneously. For $\textsc {Greedy}$, as explained above this means that every leading job $j_i'$ for $i>3$ is replaced by three simultaneous jobs. Every extra job which $\textsc {Adv}$ puts on some machine $M_i$, $i>3$ is also replaced by three jobs.

On the other hand, every time that a subinstance $(I_1',E_1')$ or $(I_2',E_2')$ is invoked within some instance $(I_k',E_k')$ for $k>3$ in $I'$, we omit this invocation and let no jobs arrive. (Thus these two subinstances are only invoked to create instances $(I_3',E_3')$, and $(I_1',E_1')$ is only invoked to create $(I_2',E_2')$.) This defines the input $I''$, cf. Fig. 2.

Fig. 2

An instance of $(I_5'',E_5'')$. The figure shows the schedule of Greedy, using the same conventions as before. The value of $\varepsilon$ is exaggerated in this figure for clarity; in the actual construction, the first (left most) nine jobs all overlap. On the left and in the middle, groups of three leading jobs are marked, which the adversary schedules on the machines indicated by the arrows. In particular, the last three leading jobs of $(I_5'',E_5'')$ are scheduled later by Adv than by Greedy, which is why there is no reason to invoke constructions of $(I_1'',E_1'')$ and $(I_2'',E_2'')$ there. In the two instances of $(I_3'',E_3'')$ that are marked by the dotted lines, the schedule of the adversary is as in the previous figure

Since $\textsc {Greedy}$ prefers faster machines and no two jobs arrive simultaneously in $I$ or $I'$ by construction and by using the precondition, this means that the schedule of $\textsc {Greedy}$ for $I''$ is determined exactly by its schedule for input $I'$: the schedule for machines $M_1,M_2,M_3$ remains the same, apart from omitting jobs that do not arrive in $I''$, whereas for $i>3$, the schedule for each machine of speed $s_i$ is the same as the schedule for the single machine of speed $s_i$ in $I'$.

$\textsc {Adv}$ again uses a cyclically shifted schedule, but now for $k>3$, jobs are shifted in groups of three: each job that $\textsc {Greedy}$ assigns to a machine of speed $s_i$ is assigned to a machine of speed $s_{i+1}$ for $i=2,\ldots ,k-1$; the leading jobs of $I_k$ on $M_1,M_2,M_3$ are assigned to machines of speed $s_4$, and the leading jobs of $I_k$ on the machines of speed $s_k$ are assigned to $M_1,M_2,M_3$. This in particular means that the leading jobs on the three slowest machines complete later in the schedule of $\textsc {Adv}$ than in $\textsc {Greedy}$, which explains why we do not create subinstances $(I_1,E_1)$ and $(I_2,E_2)$ here: there is no point in occupying the faster machines when the leading jobs on $M_2$ and $M_3$ complete in the schedule of $\textsc {Greedy}$, since $\textsc {Adv}$ is still busy running them.

It follows immediately that $\textsc {Greedy}$ schedules all the jobs in $I_m''$ and none of the jobs in $E_m''$, and it remains to calculate the numbers of these jobs. We claim that for $k>3$, $|I_k''|=16\cdot 2^{k-4}-3$ and $|E_k''|=9\cdot 2^{k-4}-3$. For $k=4$, we indeed have $|I_4''|=6+|I_3''|=13$ (there are six leading jobs, and only one subinstance, namely $I_3''$) and $|E_4''|=6$ (three jobs in $E_3''$ and three jobs for the leading jobs on the machines of speed $s_4$). For $k>4$, using the inductive assumption,

$$\begin{aligned} |I''_k|=3(k-2)+\sum _{i=3}^{k-1}|I'_i|=3(k-2)+7+16\sum _{i=0}^{k-5}2^{i}-3(k-4)=16\cdot 2^{k-4}-3 \end{aligned}$$

and

$$\begin{aligned} |E''_k|=3(k-3)+\sum _{i=3}^{k-1}|E'_i|=3(k-2)+9\sum _{i=0}^{k-5}2^{i}-3(k-4)=9\cdot 2^{k-4}-3. \end{aligned}$$

Theorem 2.6

The competitive ratio of the Greedy algorithm for interval scheduling of unit size and unit weight jobs on $m=3(k-2)$ related machines is at least $(25\cdot 2^{k-4}-6)/(16 \cdot 2^{k-4} -3)$ for $k>3$.

Proof

From the above equalities, the competitive ratio of Greedy is at least $((16\cdot 2^{k-4}-3)+(9\cdot 2^{k-4}-3))/(16\cdot 2^{k-4}-3)=(25\cdot 2^{k-4} -6)/(16\cdot 2^{k-4}-3)$. $\square$

3 A Constant Competitive Algorithm for Two Input Classes

In this section we consider two types of instances. The first type are jobs of equal sizes (of $1$), whose weights can be arbitrary. We also consider $f$-benevolent input instances with a fixed function $f$.

Algorithm Alg: On arrival of a new job $j$, do the following.

• 1. Use an arbitrary idle machine if such a machine exists.

• 2. Otherwise, if no idle machines exist, preempt the job of minimum weight among the jobs running at time $r(j)$ having a weight less than $w(j)/2$, if at least one such job exists.

• 3. If $j$ was not scheduled in the previous steps, then reject it.

Note that we do not use the speeds in this algorithm in the sense that there is preference of slower or faster machines in any of the steps. But clearly, the eventual schedule depends on the speeds, since they determine whether a job is still running at a given time.

Definition 3.1

A chain is a maximal sequence of jobs $j_1,\dots ,j_n$ that ${\textsc {Alg}}$ runs on one machine, such that $j_k$ is preempted when $j_{k+1}$ arrives ($k=1,\ldots ,n-1$). Let $[r_k,d_k)$ be the time interval in which $j_k$ is run $(k=1,\ldots ,n)$, and let $w_k=w(j_k)$, $p_k=p(j_k)$.

For a job $j'$ that ${\textsc {Alg}}$ runs, we let $d(j')$ be the maximum time such that the algorithm runs $j'$ during $[r(j'),d(j'))$. If $j'=j_{\ell }$ of some chain, then by the definition of chains, $d(j')=d_{\ell }$.

Observation 3.2

For a chain $j_1,\dots ,j_n$ that ${\textsc {Alg}}$ runs on machine $i$, $j_1$ starts running on an idle machine, and $j_n$ is completed by ${\textsc {Alg}}$. Then it holds that $r_k=r(j_k)$, $d_n-r_n=p_n/s_i$, and for $k<n$, $d_k-r_k < p(j_k)/s_i$ and $d_k=r_{k+1}$ hold.

The following observation holds due to the preemption rule.

Observation 3.3

For a chain $j_1,\dots ,j_n$, $2w_k<w_{k+1}$ for $1\le k \le n-1$.

Consider a fixed optimal offline solution ${\textsc {Opt}}$, that runs all its selected jobs to completion. We say that a job $j$ that is executed by ${\textsc {Opt}}$ is associated with a chain $j_1,\dots ,j_n$ if ${\textsc {Alg}}$ runs the chain on the machine where ${\textsc {Opt}}$ runs $j$, and $j$ is released while this chain is running, i.e., $r(j) \in [r_1,d_n))$.

Claim 3.4

Every job $j$ that is executed by ${\textsc {Opt}}$, such that $j$ is not the first job of any chain of ${\textsc {Alg}}$, is associated with some chain.

Proof

Assume that $j$ is not associated with any chain. The machine $i$ that is used to execute $j$ in ${\textsc {Opt}}$ is therefore idle at the time $r(j)$, as otherwise $j$ would have been associated with the chain running at this time on machine $i$. Thus, $j$ is assigned in step 1 (to some idle machine that is not machine $i$), and it is the first job of a chain. $\square$

Thus, in particular, every job run by ${\textsc {Opt}}$ but not by ${\textsc {Alg}}$ is associated with a chain. We assume without loss of generality that every job in the instance either belongs to a chain or is run by ${\textsc {Opt}}$ (or both), since other jobs have no effect on ${\textsc {Alg}}$ and on ${\textsc {Opt}}$.

For the analysis, we assign the weight of every job that ${\textsc {Opt}}$ runs to jobs and chains of ${\textsc {Alg}}$, and analyse the total weight of jobs assigned to a given chain compared to the weight of its last job (that ${\textsc {Alg}}$ completes). The chain can receive weight assignments as an entire chain, but its specific jobs can also receive weight assignment. The assignment of the weight of a job $j$ is split between $j$ (it will be counted later towards the weight assigned to the chain that it belongs to in ${\textsc {Alg}}$) and the entire chain of ${\textsc {Alg}}$ that $j$ is associated with, where one of the two parts can be zero. In particular, if ${\textsc {Alg}}$ does not run $j$ then the first part must be zero, and if $j$ is not associated with a chain then the second part must be zero. The assignment is defined as follows. Consider job $j$ that ${\textsc {Opt}}$ runs on machine $i$.

• 1. If $j$ is not associated with any chain, then assign a weight of $w(j)$ to $j$.

• 2. If $j$ is associated with a chain of ${\textsc {Alg}}$ (of machine $i$), then let $j'$ be the job of the chain such that $r(j) \in [r(j'),d(j'))$. Assign a $\min \{w(j),2\cdot w(j')\}$ part of the weight of $j$ to this chain, and assign the remaining weight $\max \{w(j)-2\cdot w(j'),0\}$ to $j$ itself.

For unit jobs, given a job $j'$ that belongs to a chain, there is at most one job $j$ assigned to this chain such that $r(j) \in [r(j'),d(j'))$, since ${\textsc {Opt}}$ cannot complete any job on this machine before time $d(j')$ if it is released no earlier than time $r(j')$. For an $f$-benevolent instance, multiple jobs that are associated with a chain on a machine $i$ can be released while a given job $j'$ of that chain is running, but we claim that only the last one can possibly have weight above $w(j')$. Consider a job $j$ that ${\textsc {Opt}}$ runs on $i$, that is released during $[r(j'),d(j'))$, and such that there exists at least one other job with the same properties that is released later. Job $j$ satisfies $r(j)+\frac{p(j)}{s_i}\le d(j')$ and $r(j)\ge r(j')$, so $p(j)\le p(j')$ and therefore $w(j)\le w(j')$ by the C-benevolence of $f$. The complete weight of $j$ is assigned to the chain. If there exists a job $\tilde{j}$ that ${\textsc {Opt}}$ runs on $i$, that is released during $[r(j'),d(j'))$, but is completed by ${\textsc {Opt}}$ after time $d(j')$, then $\tilde{j}$ may have some weight assigned to itself, if its weight is above $2w(j')$; however, this can happen only if ${\textsc {Alg}}$ runs this job on another machine, as we now show. If ${\textsc {Alg}}$ does not run $\tilde{j}$, then ${\textsc {Alg}}$ does not preempt any of the jobs it is running, including the job $j'$ on the machine that ${\textsc {Opt}}$ runs $\tilde{j}$ on, then $w(\tilde{j}) \le 2w(j')$ (and the weight of $\tilde{j}$ is fully assigned to the chain it is associated with ). If ${\textsc {Alg}}$ runs a job $\tilde{j}$ on the same machine as ${\textsc {Opt}}$, then $\tilde{j}=j'$ must hold, and the weight of $\tilde{j}$ is completely assigned to the chain (and not assigned to itself).

For any chain, we can compute the total weight assigned to the specific jobs of the chain (excluding the weight assignment to the entire chain).

Claim 3.5

For a chain $j_1,\dots ,j_n$ that ${\textsc {Alg}}$ runs on machine $i$, the weight assigned to $j_1$ is at most $w_1$. The weight assigned to $j_k$ for $2\le k \le n$ is at most $w_k-2w_{k-1}$. The total weight assigned to the jobs of the chain is at most $w_n-\sum _{k=1}^{n-1} w_k$.

Proof

The property for $j_1$ follows from the fact that the assigned weight never exceeds the weight of the job. Consider job $j_k$ for $k>1$. Then $w_k>2w_{k-1}$ by Observation 3.3. If there is a positive assignment to $j_k$, then the machine $i'$ where ${\textsc {Opt}}$ runs $j_k$ is not $i$. At the time $r_k$ all machines are busy (since the scheduling rule prefers idle machines, and $j_k$ preempts $j_{k-1}$). Moreover, the job $j'$ running on machine $i'$ at time $r_k$ satisfies $w(j')\ge w_{k-1}$. Thus $j_k$ is assigned $w_k - 2\cdot w(j') \le w_k-2 w_{k-1}$. The total weight assigned to the jobs of the chain is at most $w_1 + \sum _{k=2}^n \left( w_k-2w_{k-1}\right) = w_1+ \sum _{k=2}^n w_k- 2\sum _{k=1}^{n-1} w_{k}=\sum _{k=1}^n w_k - 2\sum _{k=1}^{n-1} w_{k}=w_n-\sum _{k=1}^{n-1} w_{k}$. $\square$

For a job $j$ that has positive weight assignment to a chain of ${\textsc {Alg}}$ it is associated with (such that the job $j'$ of this chain was running at time $r(j)$), we define a pseudo-job $\pi (j)$. The only goal of pseudo-jobs is to bound the total weight assigned to a chain (excluding the weight that is assigned to specific jobs of the chain). The pseudo-job $\pi (j)$ will have a weight $w(\pi (j))$ that is equal to the amount of the weight of $j$ that is assigned to the chain associated with $j$, and since this weight may be smaller than $w(j)$, its size $p(\pi (j))$ may be smaller than $p(j)$. The pseudo-job $\pi (j)$ has the same release time as $j$ and its weight is $\min \{w(j),2\cdot w(j')\}$.

If the input consists of unit jobs, then the size of $\pi (j)$ is $1$. If the instance is $f$-benevolent, then the size $p\left( \pi (j) \right)$ of $\pi (j)$ is such that $f\left( p\left( \pi (j)\right) \right) =w(\pi (j))$. We let $p \left( \pi (j) \right) = f^{-1}\left( w(\pi (j))\right)$. Note that this is well defined due to $f$’s continuity and monotonicity in $(0,\infty )$; in particular $p(\pi (j))=p(j)$ if $w(\pi (j))=w(j)$ and otherwise, when $w(j)>2w(j')$, $p(\pi (j))$ is a unique number in $\left( p(j'),p(j)\right)$.

Definition 3.6

For a given chain $j_1,\dots ,j_n$ of ${\textsc {Alg}}$ running on machine $i$, an alt-chain is a set of jobs or pseudo-jobs $j'_1,\dots ,j'_{n'}$ such that $r(j'_k) \ge r(j'_{k-1})+\frac{p(j'_{k-1})}{s_i}$ for $2 \le k \le n'$, $r(j'_1) \ge r_1$, $r(j'_{n'}) < d_n$, (that is, all jobs of the alt-chain are released during the time that the chain of ${\textsc {Alg}}$ is running, and they can all be assigned to run on machine $i$ in this order). Moreover, it is required that if $r(j'_k) \in [r_{\ell },d_{\ell })$, then $w(j'_k) \le 2\cdot w_{\ell }$.

Lemma 3.7

For unit jobs, a chain $j_1,\dots ,j_n$ of ${\textsc {Alg}}$ on machine $i$ and any alt-chain $j'_1,\dots ,j'_{n'}$ satisfy

$$\begin{aligned} \sum _{k=1}^{n'} w(j'_k) \le \sum _{{\ell }=1}^n w_{\ell }+2w_n. \end{aligned}$$

Proof

For every job $j_{\ell }$, there can be at most one job of the alt-chain that is released in $[r_{\ell },d_{\ell })$, since the time to process a job on machine $i$ is $\frac{1}{s_i}$ and thus difference between release times of jobs in the alt-chain is at least $\frac{1}{s_i}$, while $d_{\ell } \le r_{\ell }+\frac{1}{s_i}$. However, every job of the alt-chain $j'_k$ must have a job of the chain running at $r(j'_k)$. If job $j'_k$ of the alt-chain has $r(j'_k) \in [r_{\ell },d_{\ell })$ then by definition $w(j'_k) \le 2\cdot w_{\ell }$, which shows $\sum _{k=1}^{n'} w(j'_k) \le 2\sum _{\ell =1}^n w_{\ell }$.

Using $w_{k} > 2w_{k-1}$ for $2 \le k \le n$ we find $w_{k} < \frac{w_n}{2^{n-k}}$ for $1 \le k \le n$ and $\sum _{k=1}^{n-1} w_{k} < w_n$. Thus $\sum _{k=1}^{n'} w(j'_k) \le \sum _{\ell =1}^n w_{\ell }+2w_n$. $\square$

Lemma 3.8

For C-benevolent instances, a chain $j_1,\dots ,j_n$ of ${\textsc {Alg}}$ on machine $i$ and any alt-chain $j'_1,\dots ,j'_{n'}$ satisfy

$$\begin{aligned} \sum _{k=1}^{n'} w(j'_k) \le \sum _{{\ell }=1}^n w_{\ell }+2w_n. \end{aligned}$$

The proof can be deduced from a claim in the algorithm’s original analysis for a single machine [15]. For completeness, we present a detailed proof (see Appendix).

Observation 3.9

For a chain $j_1,\dots ,j_n$ of ${\textsc {Alg}}$, the list of pseudo-jobs (sorted by release times) assigned to it is an alt-chain, and thus the total weight of pseudo-jobs assigned to it is at most $\sum _{{\ell }=1}^n w_{\ell }+2w_n$.

Proof

By the assignment rule, every job that is assigned to the chain (partially or completely) is released during the execution of some job of the chain. Consider a pseudo-job $j$ assigned to the chain, and let $j'$ be the job of the chain executed at time $r(j)$.

The pseudo-job $\pi (j)$ has weight at most $\min \{w(j),2\cdot w(j')\}$. Since the set of pseudo-jobs assigned to the chain results from a set of jobs that ${\textsc {Opt}}$ runs of machine $i$, by possibly decreasing the sizes of some jobs, the list of pseudo-jobs can still be executed on machine $i$. $\square$

Theorem 3.10

The competitive ratio of ${\textsc {Alg}}$ is at most $4$ for unit length jobs, and for C-benevolent instances.

Proof

The weight allocation partitions the total weight of all jobs between the chains, thus it is sufficient to compare the total weight a chain was assigned (to the entire chain together with assignment to specific jobs) to the weight of the last job of the chain (the only one which ${\textsc {Alg}}$ completes), which is $w_n$.

Consider a chain $j_1,\dots ,j_n$ of ${\textsc {Alg}}$. The total weight assigned to it is at most

$$\begin{aligned} (w_n-\sum _{k=1}^{n-1} w_{k})+ \left( \sum _{{\ell }=1}^n w_{\ell }+2w_n\right) =4w_n, \end{aligned}$$

wherethe first summand is an upper bound on the weight assigned to individual jobs of the chain, by Claim 3.5, and the second one an upper bound on the weight assigned to the chain itself, by Observation 3.9. $\square$

4 Lower Bound for Unit Weights and Variable Sizes

We give a matching lower bound to the upper bound of $m$ shown in the introduction. Note that Krumke et al. [13] claimed an upper bound of $2$ for this problem, which we show is incorrect.

Fix $0<\varepsilon <\frac{1}{2}$ such that $\frac{1}{\varepsilon }$ is integer. Our goal is to show that no online algorithm can be better than $(1-\varepsilon )m$-competitive. We define $M=(\frac{1}{\varepsilon }-1)m$ and $N=m^3+Mm^2+Mm$. Consider a specific online algorithm ${\textsc {Alg}}$.

Input One machine is fast and has speed 1. The other $m-1$ machines have speed $1/N$. The input sequence will consist of at most $N$ jobs, which we identify with their numbers. Job $j$ will have size $p(j)=2^{N-j}$ and release time $r(j)\ge j$; we let $r(1)=1$. The input consists of phases which in turn consist of subphases. Whenever a (sub)phase ends, no jobs are released for some time in order to allow the adversary to complete its most recent job(s). ${\textsc {Alg}}$ will only be able to complete at most one job per full phase (before the next phase starts). The time during which no jobs are released is called a break. Specifically, if ${\textsc {Alg}}$ assigns job $j$ to a slow machine or rejects it, then the adversary assigns it to the fast machine instead, and we will have $r(j+1)=r(j)+p(j)$. We call this a short break (of length $p(j)$). A short break ends a subphase. If ${\textsc {Alg}}$ assigns job $j$ to the fast machine, then in most cases, job $j$ is rejected by the adversary and we set $r(j+1)=r(j)+1$. The only exception occurs when ${\textsc {Alg}}$ assigns $m$ consecutive jobs to the fast machine (since at most $N$ jobs will arrive, and $p(j)=2^{N-j}$, each of the first $m-1$ jobs is preempted by ${\textsc {Alg}}$ when the next job arrives). In that case, the adversary assigns the first (i.e., largest) of these $m$ jobs to the fast machine and the others to the slow machines (one job per machine). After the $m$-th job is released, no further jobs are released until the adversary completes all these $m$ jobs. The time during which no jobs are released is called a long break, and it ends a phase. The input ends after there have been $M$ long breaks, or if $m^2+bm$ short breaks occur in total (in all phases together) before $b$ long breaks have occurred. Thus the input always ends with a break.

Before giving the details of the analysis, we give a sketch of its structure together with the proofs of some simple properties. We will show that if there are $m^2+bm$ short breaks in total before the $b$-th long break, then ${\textsc {Alg}}$ can complete at most $b-1+m$ jobs from the input (one per long break plus whatever jobs it is running when the input ends), whereas ${\textsc {Opt}}$ earns $m^2+bm$ during the short breaks alone. This implies a ratio of $m$ and justifies ending the input in this case (after the $(m^2+bm)$-th short break).

If the $M$-th long break occurs, then the input stops. In this case, ${\textsc {Alg}}$ has completed at most $M$ jobs and can complete at most $m-1$ additional ones. ${\textsc {Opt}}$ completes at least $Mm$ jobs in total (not counting any short breaks). The ratio is greater than $Mm/(M+m)=(1-\varepsilon ) m$ for $M=(\frac{1}{\varepsilon }-1)m$.

For every long break there is a unique critical job that determines its length; this is the second largest of the $m$ jobs. Precisely, if the last $m$ jobs released before the long break are $j,\ldots ,j+m-1$, then the break has length $Np(j+1)-(m-2)=Np(j)/2-m+2=N2^{N-j-1}-m+2$ (and we set $r(j+m)$ to be $r(j+m-1)$ plus this last value). We show that it is indeed possible to complete all jobs until time $r(j+m)$. The adversary assigns job $j$ to the fast machine, where it requires time $p(j)-(m-1)$ starting from the beginning of the break (the break starts at time $r(j+m-1)$). Using $p(j)-(m-1)<Np(j)/2-(m-2)$, we see that this job completes before $r(j+m)$. After this, for $k=1,\dots ,m-1$, job $j+k$ is released at time $r(j+k)$, has size $p(j)/2^k$ and after time $r(j+m-1)$ it requires time $Np(j)/2^k - (m-1-k) \le Np(j)/2-(m-2)$, where the inequality is easily proved using $N>4m$. Note that we have $r(j+m)=r(j)+1+Np(j)/2$.

We show that at most $N$ jobs will be released as claimed. This holds because between each long break and the previous break (short or long), $m$ jobs are released, and between any short break and the previous break (short or long), at most $m$ jobs are released, out of which the last one is assigned to a slow machine by ${\textsc {Alg}}$, and the previous ones are all assigned to the fast machine. Since there are at most $m^2+Mm$ short breaks, at most $m^3+Mm^2$ jobs are released before short breaks, for a total of $m^3+Mm^2+Mm=N$ jobs.

Observation 4.1

The length of short breaks and critical jobs are decreasing at least geometrically: after a short break (critical job) of length $x$, the next short break (critical job) has length at most $x/2$ $(x/2^m)$.

For a long break $b$, let $t_b$ be the arrival time of the largest job $j_b$ that the adversary completes during this break. The critical job of this break is then job $j_b+1$. If the adversary does not create any long breaks, we let $t_1$ be the time at which the last short break (i.e., the input) finishes, and $j_1$ be the index of the last job that arrived plus one.

Lemma 4.2

For $b=1,\dots ,M$, the following statements hold.

• (i) The input ends before time $t_b+2^{N-j_b+1}(N-1)$.

• (ii) No job that is running on a slow machine in the schedule of ${\textsc {Alg}}$ can complete before the input ends.

Proof

(i) If there are no long breaks, this holds trivially. Else, the critical job of long break $b$ takes time $2^{N-j_b-1}N$ to process on a slow machine, so the total time used by the adversary to process all the critical jobs that are released after time $t_b$ is at most $2^{N-j_b-1}N(1+2^{-m}+2^{-2m}+\cdots ) =2^{N-j_b-1}N/(1-2^{-m})$ by Observation 4.1. The total length of all short breaks after time $t_b$ is at most $2^{N-j_b-m}(1+1/2+1/2^2+\cdots ) <2^{N-j_b-m+1}$ by Observation 4.1 and because the first job which is released after long break $b$ has size exactly $2^{N-j_b-m}$. At most $N$ other jobs are released at 1 time unit intervals. The total time that can pass after time $t_b$ until the input ends is thus at most $\frac{2^{N-j_b-1}N}{1-2^{-m}}+2^{N-j_b-m+1}+N.$ This is less than $2^{N-j_b+1}(N-1)$ if

$$\begin{aligned} N\left( \frac{2^m}{2^m-1}+2^{j_b+1-N}\right) +2^{2-m}<4N-4 \end{aligned}$$

Using $j_b\le N$, this holds if $N(2-\frac{2^m}{2^m-1})>2^{2-m}+4$, which is true for $N>4\cdot \frac{2^m+1}{2^m}\cdot \frac{2^m-1}{2^m-2} =4\cdot \frac{2^{2m}-1}{2^{2m}-2^{m+1}}$. For $m\ge 2$, this last expression is at most 8, and we have $N>m^3\ge 8$.

(ii) If $t_b=1$, there is nothing to show: ${\textsc {Alg}}$ does not run any job of the first phase on a slow machine. If $b>1$ and there are no jobs between long break $b-1$ and the jobs that the adversary completes during long break $b$, then the claim follows by induction: no new jobs were started by ${\textsc {Alg}}$ on slow machines after the previous long break.

In the remaining cases (including the case where there are no long breaks), job $j_b-1$ was placed on a slow machine by ${\textsc {Alg}}$ and caused a short break. Thus it was released at time $t_b-2^{N-j_b+1}$ and ${\textsc {Alg}}$ can complete it at the earliest at time $t_b-2^{N-j_b+1} + 2^{N-j_b+1}N=t_b+2^{N-j_b+1}(N-1)$, by which time the input has ended by (i).

If $b>1$, then by induction, no job that was released before the jobs which led to long break $b-1$ can be completed by ${\textsc {Alg}}$ on a slow machine before the input ends. We will now lower bound the completion time of the other (more recent) jobs on the slow machines (if they exist), also for the case $b=1$. Each such job caused a short break.

We first consider a simple case, where all these jobs were released consecutively immediately before the jobs which led to long break $b$. In this case, the $k$-th such job (counting backwards from time $t_b$) was released at time $t_b-2^{N-j_b+1}(1+2+\dots +2^{k-1}) \ge t_b-k2^{N-j_b+k}$ and does not complete before time $t_b+(N-k)2^{N-j_b+k} > t_b+(N-1)2^{N-j_b+1}$, so we are again done using (i). The inequality holds because $N(2^{k}-2) > k2^{k}-2$ which is true for all $k\ge 2,N\ge k+1$.

Note that this proves that any job which is released during an arbitrarily long sequence of consecutive short breaks that immediately precedes a long break can only finish (on a slow machine) after the input ends. There may also be jobs that ${\textsc {Alg}}$ assigns to the fast machine in between. Consider all such jobs starting from the last one before time $t_b$. We can insert these jobs one by one into the sequence, starting from the end. The effect of each insertion is that the release time of all preceding jobs is decreased by 1 compared to the calculations above, whereas their sizes are doubled. Thus after any such job is inserted, we still have that no job which ${\textsc {Alg}}$ is running at time $t_b$ on a slow machine can complete before the input ends. $\square$

Lemma 4.3

${\textsc {Alg}}$ cannot complete any job on the fast machine except during long breaks.

Proof

First, consider any maximal set of consecutive jobs that ${\textsc {Alg}}$ assigns to the fast machine. By construction, these jobs arrive at consecutive integer times, and all except maybe the very last one of the input has size more than 1. This shows that ${\textsc {Alg}}$ could only possibly complete the last job of each such set. If the set has size $m$, this happens during the long break that follows. This can be seen as follows. Consider long break $b$. The adversary completes job $j_b+1$ which has size $2^{N-j_b-1}$ on a slow machine during this break. The job that ${\textsc {Alg}}$ assigned to the fast machine when break $b$ started is job $j_b+m-1$, which arrives at time $t_b+m-1$ and has size $2^{N-j_b-m+1}$. Since $m-1+2^{N-j_b-m+1}<N2^{N-j_b}$, ${\textsc {Alg}}$ completes it during the long break.

For a set of size less than $m$, at least one short break starts one time unit after the last job in the set arrives. Say this last job has size $2^{N-j}$. Then the short break which follows has size $2^{N-j-1}$, and by Observation 4.1, the total length of all possible later short breaks is at most $2^{N-j-1}(1+1/2+\dots +1/2^{-m^2-Mm})<2^{N-j}$. So the job of size $2^{N-j}$ cannot complete before either the input ends or another job is assigned by ${\textsc {Alg}}$ to the fast machine. $\square$

It follows from Lemmas 4.2 and 4.3 that after the $b$-th long break, ${\textsc {Alg}}$ has completed at most $b$ jobs (the ones that it was running on the fast machine when each long break started), and none of the jobs that were released so far and that were assigned to slow machines can complete before the input ends.

Appendix: Proof of Lemma 3.8

The proof is an induction on $n$. Since we only consider the execution of jobs on a specific machine $i$, we use terms such as “contained”, “completion time”, and “a job is released during the execution of another job”.

Consider a chain $j_1,j_2,\ldots ,j_n$. Let ${\textsc {Alg}}_n=\sum _{k=1}^n w_k$ be the total weight of all jobs in this chain. Denoting by ${\textsc {Alt}}_n^*$ the maximum possible total weight of jobs of an alt-chain of the chain $j_1,j_2,\ldots ,j_n$, we are to prove that

$$\begin{aligned} {\textsc {Alt}}_n^* \le {\textsc {Alg}}_n + 2w_n. \end{aligned}$$

We are going to prove a stronger claim. Call an alt-chain proper if it is contained in its corresponding chain, i.e., if its last job ends before $d_n$, and let ${\textsc {Alt}}_n$ be the maximum possible total weight of jobs of a proper alt-chain of the chain $j_1,j_2,\ldots ,j_n$. Then it suffices to prove

$$\begin{aligned} {\textsc {Alt}}_n \le {\textsc {Alg}}_n , \end{aligned}$$

(4)

since any alt-chain that is not itself proper becomes proper when its last job, of weight at most $2w_n$ by definition of a chain and an alt-chain, is removed.

Recall that job interval of $j_{\ell }$ may be shorter than $\frac{p_{\ell }}{s_i}$ due to a preemption. For a chain with $n$ jobs, every prefix can be seen as a chain as well, only the last job of the prefix may be preempted in the complete chain.

The base case of $n=0$ and an empty chain holds trivially.

Consider a chain of length $n>0$. If there is no job released during $[r_{n},d_{n})$, the last released job has weight at most $2w_{n-1}$ by definition, and the preceding jobs form a proper alt-chain for the chain $j_1,\dots ,j_{n-1}$. By induction, the total profit of the entire proper alt-chain is then at most ${\textsc {Alg}}_{n-1}+2w_{n-1}<{\textsc {Alg}}_n$.

Else, we merge all jobs released during $[r_{n},d_{n})$ into one job. Merging the two last jobs $a$ and $b$ of a proper alt-chain is done as follows. The two jobs are replaced by job $c$ with weight $w(c)=w(a)+w(b)$ and size $p(c)=f^{-1}\left( w(c)\right)$, determined by the C-benevolent function $f$ (corresponding to the instance).

The resulting job is placed so that it ends precisely at $d_n$, the end of the chain. Note that when $c$ is formed by merging $a$ and $b$, $p(c) \le p(a) + p(b)$ since $f$ is convex, and therefore the job formed by merging two jobs starts no earlier than the earliest of those jobs. This extends naturally to merges of more than two jobs. After merging the suffix contained in $[r_{n},d_{n})$, the resulting set of jobs forms a proper alt-chain with smaller cardinality but the same weight. The last job has weight at most $w_n$.

After merging the jobs contained in $[r_n,d_n)$, denote the resulting job by $b$. If the penultimate job $a$ of the alt-chain ends no later than at $d_{n-1}=r_n$, the jobs before $b$ form a proper alt-chain for the chain $j_1,\dots ,j_{n-1}$. By induction, the total profit of the entire proper alt-chain is then at most ${\textsc {Alg}}_{n-1}+ w_{n}={\textsc {Alg}}_n$.

Else, $a$ weighs at most $2w_{n-1}<w_n$ by definition of the alt-chain. Note that both $a$ and $b$ weigh less than $w_n$, and therefore have size at most $p_n$. If $a$ is larger than $b$, swap the two jobs while preserving the end time of the later one, and the start time of the earlier one. Rename them so that again $a$ is followed by $b$. If $a$ now finishes before $d_{n-1}$, we are done as before.

Let $L$ be the total size of $a$ and $b$, $t_1$ the release time of $a$, and $t_2$ its completion time, $t_3$ the release time of $b$, and $t_4$ its completion time. By possibly extending $b$, we can assume that $t_2=t_3$ and $t_4=d_{n+1}$. Now increase the size of $b$ up to $p_n$, i.e., by $p_n-p(b)$, decreasing the size of $a$ and the release date of $b$ by the same amount. As this increases the size of the larger job, by convexity of $f$, the total weight of $a$ and $b$ does not decrease in the process. Afterwards, $a$ and the preceding jobs form an alt-chain properly contained in the chain $j_1,\ldots ,j_{n-1}$, while $b$ has weight $w_n$. We are done by induction.