Introduction

Vibration of infrastructures and platforms results in many cases to the damage and failure of these structures. Vibration are caused by natural and artificial sources. In any case, these vibrations need to be measured to be controlled [1] or used as a source of energy and converted into electricity [2,3,4]. In this article, we focused on the determination of vibration measurement in rotating machines. The determination of accurate measurement of blade’s vibration and their analysis have gained huge importance in these recent years[5,6,7]. Infrastructures, such are turbines, compressors, vans, and wind power plants, are always operating in harsh environments inducing their vibrations [8, 9]. The blades in such infrastructures are the most exposed to these vibrations and their defaults or damages could lead to the reduction of the efficiency of the infrastructures, and in the worst case, their operations are interrupted [10,11,12]. Thus, monitoring the blades could avoid such problems. This monitoring passes through the determination of the blade vibration’s measurements and their analysis to identify the source of vibrations (through the determination of the frequencies of excitation) and severity of the excitation through the determination of the amplitude of vibration of the blades [13, 14].

Two particular methods are traditionally used for the determination and the characterisation of the blade’s vibration: the contact and the non-contact methods [14,15,16]. The contact method is particularly based on the strain gauge, which is a sensor fixed on the surface of the blade, where the properties enable the identification of the frequencies and amplitudes of vibration of the monitored blade [14, 17]. The non-contact method is mostly done through the blade tip timing (BTT) using sensors arranged on the circumference of the engine casing, and enables the monitoring of all the blades of the bladed assembly by collecting the time each tip blade passes underneath the sensors [14, 18, 19]. Many studies have pointed out the differences between the two monitoring methods. We are particularly focused on the monitoring of all the blades; thus, the BTT method is the one used in this work, despite the fact that data collected through this method are extremely under-sampled, mostly due to the limited number of sensors or probes which can be mounted in the engine casing. A way to reduce the impact of this drawback is to propose an optimal arrangement of the probes to get useful data [20]. Thus, this work assumed that the frequency of vibration of the blades is known, and proposed a method based on the minimisation of the root-mean-square error (RMSE) of the amplitude of interest among other variables, to propose the optimal probe arrangement.

The rest of the article is composed as follows: the next section presents the basic principles of the BTT. Uncertainties and errors often present in BTT measurements will be shown in section 3. The fourth section presents the optimization steps for the probe arrangement, while the fifth section presents and discusses the results obtained, and in the last section, we will conclude this work.

Basic Principles of the BTT

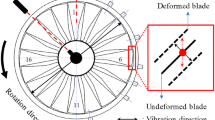
Blade tip-timing method is a non-contact method constituted of probes placed in the circumference of the engine casing. It is based on the determination of the blade vibration until the blade passes underneath the probes, well known as time of arrival (TOA) [5] (see Fig. 1).

Fig. 1
figure 1

Blade vibration measurements using the BTT methods

Full size image

Thus, let us assume that we have a bladed-disk assembly composed of N blades and rotating with an angular velocity \(\Omega\) (in rad/s). The blades are located by their angular position \(\alpha _{i}\), such that

$$\begin{aligned} \alpha _{i}=\frac{2\pi i}{N}, \end{aligned}$$

with \(i=1,2,\dots , N\). The BTT system, on the other hand, is constituted of L equally distant probes arranged around the engine casing. The probes are located by their angular position \(\theta _{j}\), such that

$$\begin{aligned} \theta _{j}=\frac{2\pi j}{L}, \end{aligned}$$
(1)

with \(j=1,2,\dots , L\). The process of identification of the blade vibration parameters is given in Fig. 2. It starts with the definition of the number of probes to be mounted and their different positions in engine casing. The next step consists of the determination of the TOA of the blade underneath a sensor and it is described as follows: Let us denote by \(t_{\text {act}}\) and \(t_{\text {exp}}\) the actual arrival time and the expected arrival time, respectively, of a random blade underneath a random probe. The actual time is the time measured during the experiment, the one called earlier TOA, while the expected time corresponds to the time at which the blade should pass underneath the probe for a blade rotating with a constant speed and without vibration. For a non-vibrating blade

$$\begin{aligned} t_{\text {act}}=t_{\text {exp}}, \end{aligned}$$

and for a vibrating blade

$$\begin{aligned} t_{\text {act}}\ne t_{\text {exp}}. \end{aligned}$$

Thus, the sign of the difference \(t=t_{\text {act}}-t_{\text {exp}}\) indicates whether the blade arrives in advance (\(t>0\)) or with a delay (\(t>0\)) underneath the probe. The determination of the tip deflection x of the blade is therefore deduced from the following expression:

$$\begin{aligned} x=\Omega R t, \end{aligned}$$

where R is the distance of the extremity of the blade from the center of the engine shaft.

The described principle of BTT system constitutes the data acquisition part of the whole process of identification of the vibration parameter of the blade.

Fig. 2
figure 2

Schematic representation of the whole process of identification of the blade vibration parameters

Full size image

Once the acquisition of data is done, the next step consists of the processing of the data to determine the vibration parameters [14, 21,22,23]. In BTT measurement analysis, data processing starts with a proposition of a mathematical model assumed to reproduce the vibration of the blade. Generally, a combination of sine and cosine function is used, as the one given by Eq. (2) to model the tip displacement of the blade \(y_{t}\) at a time t

$$\begin{aligned} y_{t}=d + \sum _{k=1}^{m}\left( \beta _{ks}\sin (2\pi \times f_{k}t)+ \beta _{kc}\cos (2\pi \times f_{k}t)\right) , \end{aligned}$$
(2)

where m, \(\beta _{ks}\), \(\beta _{ks}\), and \(f_{k}\) are the total number of mode considered, sine, cosine coefficients and the frequency of the mode k, respectively, and t is the time of passage of the blade underneath a probe. This equation can be re-written as a function of the angle swept by the rotating blade, the engine order (ratio between the blade vibration frequencies and the frequency of rotation of the blade) using the following expression:

$$\begin{aligned} \theta (t)+ 2\pi n =2\pi ft , \end{aligned}$$

where n is the number of revolutions made by the blade and f is the frequency of rotation of the blade. In addition

$$\begin{aligned} f_{k}=EO_{k}f, \end{aligned}$$

by substituting the latest equations in Eq. (2)

$$\begin{aligned} y_{t}=d + \sum _{k=1}^{m}\left( \beta _{ks}\sin (\text {EO}_{k}(\theta (t)+2\pi n)+ \beta _{kc}\cos (\text {EO}_{k}\theta (t)+ 2\pi n)\right) . \end{aligned}$$
(3)

Equation (3) gives the mathematical expression of the original vibration signal of the blade as a function of the angle swept and the engine order of all the mode of vibrations, with \(\text {EO}_{k}\) being the engine order of the mode k. In the case of purely synchronized vibration without any noise in the measurements, one can drop the term \(2\pi n\) because of the \(2\pi -periodicity\) of the sine and cosine functions. The Ordinary Least Square (OLS) method is, therefore, employed to determine the parameters \(\beta _{ks}\), \(\beta _{kc}\) and d, from which the amplitudes of vibration of the blade are derived [23,24,25].

Review of Blade Tip-Timing Methods

In the previous section, the principle of BTT system, as well as the mathematical modeling of the blade vibration, have been established. Thus, it will be presented in the current section, the existing BTT methods. The turbine blades in general, when excited, can exhibit asynchronous vibration, synchronous vibration, or the combination of asynchronous and synchronous vibration.

Tip-Timing Methods for Blade Asynchronous Vibration Responses

Several studies in BTT systems proposed the use of sensors placed at equally spaced locations around the casing to analyze asynchronous vibration of the blade. This, for ensuring that the vibration responses of the blades are also equally spaced in time [14], but such a type of configuration has been proved to be highly influenced by the probe spacing on resonance and may record the same vibration information in the case of synchronous vibration [26].

  • The simplest asynchronous BTT system

The simplest BTT method is the one composes by a single probe. The method is employed to determine the average blade amplitude of vibration at a constant rotation speed. The first single probe method was proposed by Rudolph Hohenberg in 1967, who used an optical probe to determine the amplitude of asynchronous vibration response of the bladed-disk assembly from the measurement of a single blade tip response parameter [27].

  • BTT system with more than one probe

There exist various BTT systems for asynchronous vibration inference using more than one probe and able to determine in general, the amplitude, phase, and frequency of vibration of the blades by several techniques including the curve fitting and spectrum analysis methods. For BTT system using two probes, one can list the work done by Lawson and Ivey, who have used two capacitance sensors to identify vibration parameters of the blade [28]; Yue et al. used in [29] a validated parameter identification using two probes combined to the all phase FFT. Zielinski et al. proposed two BTT systems using three and five equally spaced with the angular separation of 120 \(^\circ\) and 72\(\,^\circ\), respectively [24]. In this last case, the Fourier transform is used to determine the maximal amplitude of vibration and the waterfall diagram was used for the identification of the vibration modes [24]. Those studies using two probes include the one by Krause et al. and Bastani et al. [21, 30]. BTT system for the determination of the asynchronous vibration parameters using seven probes has been proposed by Zhang et al. [31], where the seven probes are separated into two groups of five equally spaced probes for the first group and three equally spaced probes for the second group, with a probe belonging to the two groups. This system is also known as the ‘5+3’ BTT scheme. These configurations allow, therefore, to generate five and three uniformly distributed samples. The analysis of the collected vibration signals is done using the FFT combined with the Campbell diagram [31].

Tip-Timing Methods for Blade Synchronous Vibrations

Synchronous vibration response is harder to monitor using blade tip timing compared to the asynchronous vibration at a constant rotation speed and without any type of fluctuations. This is due to the fact that the sensors detect the blade tip always at the same phase, meaning that the blade’s measured tips’ displacement is constant over multiple revolutions. Another major problem in synchronous vibration is the difficulty to monitor such vibrations when more than one mode of vibration are excited. This requires BTT methods to be able to extract amplitudes and frequency of vibrations corresponding to these modes of excitation. Blade tip-timing method in this case is divided into direct and indirect analysis methods.

  • Direct methods:

Direct analysis methods are based on the collection of data from at least four probes [9, 14] on each assembly rotation for the same operating conditions. These samples are analyzed using a least-squares sine fit to infer the maximum vibration amplitude and frequency starting from the equation of vibration of the blade at a given frequency of vibration. Examples of direct analysis methods include the Determinant (DET) method [17], the Auto-Regressive method (AR), the Global AR (GAR) methods, the GAR with Instruments Variables (GARIV), the Multi-frequency AR methods (MAR, MGAR, MGARIV), and the multi-Revolutions formulations methods [23].

  • Indirect methods

Indirect analysis methods, on the other hand, require less probes than the direct methods; usually, one or two measurement locations at each assembly revolution are enough to extract vibration information of the blade. Which is done varying the rotational speed of the assembly, which results on sweeping the range of frequencies around the natural frequency of the assembly [32]. Examples of indirect method include the Zabolsky and Korostolev technique, well known as a single parameter method; the two parameter plot method and its derivations  [14, 33].

Frequency Spectrum Analysis Methods

The frequency spectrum analysis method is based on the determination of the vibration frequencies from the tip displacement data, through different methods such as the Fourier analysis method, CS, and the SR with associated algorithms.

  • Fourier Analysis method

One way to apply the Fourier analysis on the BTT method is to analyze the tip displacement corresponding for individual blade separately (single blade analysis) and the other way is to include the tip displacement of all the blades in the order they were collected (All-blade spectrum analysis)  [14]. If the system is dominated by a single resonance and in the absence of noise, then the Fourier spectrum could identify with very good accuracy the frequency of that resonance.

  • Sparse Reconstruction/Compressed Sensing

The sparse reconstruction/compressed sensing method has recently been proposed to extract the blade vibration frequency from under-sampled BTT data. This method is able to retrieve a multi-modes blade tip-timing vibration signals. It does so in two important steps: The sparse representation and the multi-mode vibration reconstruction algorithm. In the sparse representation step, the mathematical model for sparse BTT signal is built and yields to an SR problem. The second step consists, therefore, in the elaboration of an algorithm, namely the multi-mode vibration reconstruction algorithm to solve the sparse representation problem. A full and detailed description concerning this method can be found in [34,35,36].

Uncertainty in Blade Tip-Timing Measurements

Measurements taken in BTT system as in many physical systems are subjected to uncertainties or errors of diverse origins, which play a key role on the accuracy of the measured quantities.

In general, errors in measurements or data can find their origins in the measurement instruments, the environment, the method used for processing these acquired data, and so on. The error is defined as the difference between the measured value and the exact value of the quantity being measured. There exist three categories of errors such as:

  • Systematic errors, also called bias, are usually caused by the measuring instruments, and it is repeated in all the measurements obtained by these instruments. This type of error can be suppressed by a good calibration of the instruments used.

  • Random error, also known as a statistical error, is always present in measurements. This type of error is unpredictable, meaning that it affects the measurements by different amounts. The source of the random error is unknown and therefore cannot be corrected.

  • Gross error or blunder is either caused by the measuring instrument failures or by the experimenter’s mistakes. Such error can be detected in the measured value, in which the gap between the exact value is large. This error can be avoided by carefully checking the measuring instruments and by repeating the measurements many times.

In metrology, doubts about measurement are called measurement uncertainty. Measurement uncertainty roughly speaking is a parameter used in data processing for the description of both the dispersion of the result and its estimated difference from the accurate value. Measurement uncertainty quantifies, therefore, the contributions in the measurements of unpredictable errors. Thus, the determination of the measurement uncertainty consists of the statistical analysis of the measurements to determine the dispersion of the measurement [variance (var), standard deviation (std), RMSE, and so on] and the difference between the average of the measurement and the exact value of the quantity has been measured. Uncertainty can likely be found in many measuring systems including blade tip-timing systems. Thus, Pete in [16] listed the source of uncertainties in the data, which are grouped into three categories: uncertainties due to the probe positioning, uncertainties due to the pre-processing of the acquired data, and the uncertainties due to the conversions, including the conversion of the TOA to deflection and frequency, and the conversion of the obtained deflection into blade stress.

In many works on the evaluation of the uncertainty measurement in BTT, the overall uncertainties are often considered as a Gaussian white noise. Thus, it is added in the mathematical model of the blade vibration signal given by Eq. (2) a Gaussian white noise \(\xi _{t}\). Thus, the mathematical model of the vibration signal is then given by Eq. (4)

$$\begin{aligned} y_{t}=d + \sum _{k=1}^{m}\left( \beta _{ks}\sin (2\pi \times f_{k}t)+ \beta _{kc}\cos (2\pi \times f_{k}t)\right) +\xi _{t}. \end{aligned}$$
(4)

Optimization Process for Probe Arrangements

The optimization of the probe positions is based on the minimization of the RMSE of the amplitude of the mode k obtained using Eq. (4). The optimization process of the probe positioning in the present BTT system is constructed through the following steps:

  • Choose the angular or time resolution to work with: It is defined the number of possible probes location, which is equivalent to defining the number of segments of time \(N_{\text {seg}}\) in which data are recorded at a single rotation of the bladed disk assembly. Thus, we denote by \(\delta\) the angular resolution, such that the total number of recorded measurements in a revolution is given by

    $$\begin{aligned} N_{\text {seg}}=\frac{2\pi }{\delta (\text {rad})} \left(\frac{360^{\circ }}{\delta (^{\circ })}\right). \end{aligned}$$
    (5)

    Thus, going from the principle that a non-vibrating blade with an angular velocity \(\Omega =2\pi f=\frac{2\pi }{T_{\text {rot}}}\) completes a cycle or a turn at the time \(T_{rot}\) being the period of rotation of the turbine. Thus, the non-vibrating blade will pass exactly underneath the probes, where the locations are given by

    $$\begin{aligned} \theta =\{0, \delta , 2\delta , \dots , i\delta , \dots , 360\}, \end{aligned}$$

    with \(\delta\) in \((^{\circ })\), at the corresponding time

    $$\begin{aligned} t=\left\{0, \frac{T_{\text {rot}}}{N_{\text {seg}}} ,2\frac{T_{\text {rot}}}{N_{\text {seg}}}, 3\frac{T_{\text {rot}}}{N_{\text {seg}}},\dots , j\frac{T_{\text {rot}}}{N_{\text {seg}}},\dots , T_{\text {rot}}\right\}. \end{aligned}$$

  • Choose a setup: We define the number of probes (r) to be mounted in the engine casing. From the defined number of probes, possible r-probe positions are generated. This is achieved by the choice of r probe placement within the \(N_{\text {seg}}\) possibles.

  • Choose the true model: The mathematical model to guess the blade tip vibration signal is proposed. For this work, the model given by Eq. (4) is chosen.

  • Choose the simulation setup: We define the length of the time series T and the number of time series M. In fact, the number T represents somehow the total number of cycles completed by the rotating blade, such that the time series will be given by the set

    $$\begin{aligned} \begin{aligned}&t=\{0, \frac{T_{\text {rot}}}{N_{\text {seg}}} ,2\frac{T_{\text {rot}}}{N_{\text {seg}}}, 3\frac{T_{\text {rot}}}{N_{\text {seg}}},\dots , j\frac{T_{\text {rot}}}{N_{\text {seg}}},\dots , T_{\text {rot}}, T_{\text {rot}}+\frac{T_{\text {rot}}}{N_{\text {seg}}} ,T_{\text {rot}}+2\frac{T_{\text {rot}}}{N_{\text {seg}}}, T_{\text {rot}}+3\frac{T_{\text {rot}}}{N_{\text {seg}}},\\&\quad \dots ,T_{\text {rot}}+ j\frac{T_{\text {rot}}}{N_{\text {seg}}},\dots , 2T_{\text {rot}},\dots , TT_{\text {rot}}\}. \end{aligned} \end{aligned}$$

  • Estimation of the statistical variables: At this stage and for the ensemble of r-probe positioning, it is estimated for the M time series, the amplitude of vibration of the different mode \(\hat{A}_{k}\) is determined using the OLS method with the python programming language, the standard deviation (\(\text {std}_{k}\)), the bias (\(bi_{k}\)), and the Root-Mean-Squared Error (\(\text {RMSE}_{k}\)) of the amplitudes of vibration.

  • Optimization: The optimisation consists of choosing the r-probe positioning with the smallest RMSE for different modes.

These statistical variables are obtained through the following formulations:

$$\begin{aligned}&\hat{A}_{k}=\sqrt{\hat{\beta }_{sk}^2 + \hat{\beta }_{ck}^2} \end{aligned}$$
(6)
$$\begin{aligned}&bi_{k}=\frac{\sum _{m=1}^{M}(\hat{A}_{mk}-A_{k})}{M} \end{aligned}$$
(7)
$$\begin{aligned}&\text {std}_{k}=\sqrt{\frac{\sum _{m=1}^{M}{\hat{A}_{mk}}}{M}- \frac{ \sum _{m=1}^{M}{\hat{A}_{mk}^2} }{M} } \end{aligned}$$
(8)
$$\begin{aligned}&\text {RMSE}_{k}=\sqrt{\frac{ \sum _{m=1}^{M}{( \hat{A}_{mk} - A_{k} )}^2}{M}}; \end{aligned}$$
(9)

\(A_{k}\) denotes the true amplitude of vibration of the mode k, and M is the total number of time series to be considered in the optimisation and \(m=1,\dots ,M\).

Thus, after obtaining the different optimized r-probe positioning corresponding to the different mode of vibration, the final r-positioning to be mounted in the engine casing will depend of the mode of interest. The choice of the mode of interest can depend on the severity of the corresponding mode in the vibration of the blade. If all the modes of vibrations are of interest, another way to select the r-probe positioning could be done by choosing the one minimizing the average RMSE of the amplitudes of vibration of all the modes.

In turbo-machinery, blade can vibrate with one or many frequencies. Depending on the frequency of vibration and on the rotating speed of the blade, one can find synchronous vibrations, asynchronous vibrations, or the combination of both types of vibrations. In this work, many scenarios are considered. As first scenario, the blade is assumed to vibrate with a single frequency \(f_1=300 Hz\), with a phase \(\pi /4\) and the real amplitude of vibration is \(A_{1}=141.42\) \(\upmu \text {m}\). The second scenario assumes that the blade vibrates with three frequencies \(f=\left[ f_{1},f_{2},f_{3}\right] =\left[ 50,170,240\right]\) with the corresponding phase \(\left[ \pi /4, \pi /4, \pi /4\right]\) and amplitudes \(A=\left[ A_{1}, A_{2}, A_{3}\right] =\left[ 1.414214, 1.414214, 0.2\right]\). The vibrations in all the scenarios are assumed to be corrupted by a normal distributed noise \(N(\mu ,\sigma ^{2})\), with \(\mu\) and \(\sigma\) being the mean and the standard deviation of the noise, respectively. \(\sigma\) here is taken equal to \(10\%\) of the minimal amplitude of vibration of the blade. The turbo-machinery is also assumed to rotate with a constant rotation speed \(\Omega =2\pi \times 50\) rad/s.

Results and Discussion

As it is described above, one of the first step in BTT measurements is the definition of the required number of probes to be mounted. The type of probe configuration is the result of the optimization process. It is worth noting that in this work, there is a geometrical restriction on the placement of the probes. In fact, due to some technical reasons in practice, the probes can only be placed on the upper half part of the engine casing. One can add to this probe placement restriction the restriction about the space between consecutive probes. This last restriction is not considered in the present work. In addition, at the laboratory, the turbine is operating in vacuumed space where the blades are excited by electromagnetic forces generated by electromagnets. In that condition, the temperature of the electromagnets due to the flow of the current across their coils is rising. This increase of the temperature modifies the condition of performing the experiment. Thus, the recording of data is realized at many steps denoted here by M. The recorded time series of each step which is about an hour is denoted by T, and it is called length of the time series as mentioned earlier. Due to the fact that the numerical simulations performed here are extremely time consuming, the length of the time series and the number of realisation will be taken lower than the ones in practice. It is also assumed that value of the angular resolution to be \(\delta =20^{\circ }\), and the value \(r=3\) of the number of probes to be mounted in the engine casing is chosen. Thus, one can count about 816 possible probes placement in the engine casing.

Optimal Probe Positioning for the First Scenario

We apply the previously described optimization method in the case of a rotating blade vibrating with a known frequency \(f_{1}=300\) Hz and with a known amplitude \(A_{1}=141.421\) \(\upmu \text {m}\).

Table 1 reports the ranking of the probe positioning obtained from the optimization process in the first scenario. Each winner probe configuration corresponds to the one with the minimal value of one of the statistical variables.

Table 1 Report of the probe positioning of the BTT measurement system after the optimization process based on the minimization of the bias, standard deviation, and the RMSE of the amplitude of the frequency of vibration
Full size table

The probe arrangement (3, 5, 8) has the smallest value of the RMSE and the standard deviation, while (0, 1, 8) corresponds to the smallest value in absolute value of the bias. According to the RMSE optimization process, the probe placement (3, 5, 8) is, therefore, the one from which the amplitude of vibration of the blade can be determined with the highest accuracy. Table 2 reports the ranking of the probe positioning obtained from the optimization process minimizing the RMSE of the amplitude of vibration of the blade.

Table 2 Report of the probe positioning of the BTT measurement system after the optimization process based on the minimization of the RMSE of the amplitude of the frequency of vibration
Full size table

Comparing the values of the RMSE corresponding to the top five of the best probe positioning, one observes the correlation between the standard deviation and the RMSE of the amplitude of vibration: the optimal probe positioning obtained by minimizing the RMSE is the same than the one obtained by minimizing the standard deviation. Thus, the optimal probe positioning according to this optimization process is given by the following subset: (3, 5, 8). In addition, the probes positioning colored in red represent the probe arrangement constituted of probes located at the two sides of the engine casing (upper half and lower half part). As mentioned earlier, these probe positioning should be excluded from the selection. The rest of the arrangements including the green one are all irregularly spaced. This observation confirms the assertion stating that the determination of the parameters of a synchronous vibration is better when the probes are irregularly spaced, at least for synchronous vibrations.

Optimal Probe Positioning for the Second Scenario

In the second scenario, the blade exhibits simultaneously synchronous and asynchronous vibrations with respect to the blade rotation speed. The parameters of this scenario are: \(f=\left[ f_{1},f_{2},f_{3}\right] =\left[ 50,170,240\right]\) with the corresponding phase \(\left[ \pi /4, \pi /4, \pi /4\right]\) and amplitudes \(A=\left[ A_{1}, A_{2}, A_{3}\right] =\left[ 1.414214, 1.414214, 0.2\right]\).

Table3 shows the selected sensors placement for RMSE optimization of estimation of the amplitudes of different frequencies. Thus, we denote by \(\text {RMSE}_{1},\text {RMSE}_{2},\text {RMSE}_{3}\) the RMSE of estimation of the amplitude \(A_{1}\), \(A_{2}\), and \(A_{3}\), respectively.

Table 3 Report of the probe positioning of the BTT measurement system after the optimization process based on the minimization of the RMSE of the amplitudes of the frequencies of vibration
Full size table

Table 3 gives a complete report of different optimal probes placement accompanied with the bias, standard deviation, and RMSE of estimate of the amplitudes of the frequencies. It clearly appears the difficulty of choosing a probe positioning enables to retrieve accurately the ensemble of the amplitudes. Given the case if the experimenter is concerned with a particular frequency, the choice is easily made looking at the set of probes given the minimal RMSE of the estimate amplitude of the corresponding frequency.

In a case if all the frequencies are of interest, it is proposed to choose the set of probes for which the average over all the probes of the RMSE of the estimate amplitudes is minimal. Thus, Table 4 gives the optimal probes placement obtained after the late optimization process. The reported subsets of probes have been chosen for the upper half part of the engine casing. The probe positioning (0, 2, 3) is the winning probe subset.

Table 4 Report of the probe positioning of the BTT measurement system after the optimization process based on the minimization of the average of the RMSE of the amplitude of the frequency of vibration
Full size table

One observes that the values of the \(\text {RMSE}_{1}\), \(\text {RMSE}_{2}\) and \(\text {RMSE}_{3}\) determined from the probe placement (0, 2, 3) are about \(4.16\%\), \(2.34\%\) and \(12.23\%\) greater than the corresponding \(\text {RMSE}_{1}\), \(\text {RMSE}_{2}\), \(\text {RMSE}_{3}\) from the probe optimal positioning (1, 2, 3), (0, 2, 7), and (0, 3, 6), respectively.

Choice of the Probes Configuration: Regular or Irregular?

The previous analysis dealt with the determination of the optimal probe placement through the minimization of the RMSE of estimate amplitude of interest and the minimization of the average of the RMSEs of estimate amplitudes of vibration when all the vibrations are of interests. In this section, we propose to find the proportion of optimal regular and irregular probe configuration for which the corresponding RMSE is lower than a defined minimal. Thus, a simple statistical model is done to find the proportion of regularly and irregularly spaced probes configuration lower than certain value of the RMSE. In this statistical analysis, it is only considered that the probes located on the upper half part of the engine casing. Thus, let us define by \(P[\text {RMSE}_{k}<\gamma ]\) the proportion or the probability of regularly and irregularly probes configuration, for which the \(\text {RMSE}_{k}\) of estimate amplitude \(\hat{A_{k}}\) is lower or equal to a minimal value \(\gamma\). We define \(N_{\text {reg}}\) and \(N_{\text {irreg}}\) as the number of regularly and irregularly spaced probes, which the corresponding \(\text {RMSE}\) is lower than a minimal respectively. And we denote by \(N_{\text {up}}\) the corresponding total number of upper half probe placement, such that: \(N_{\text {up}}=\) \(N_{\text {reg}}\) + \(N_{\text {irreg}}\). Thus, the probability to have a regularly or irregularly spaced probes positioning lower that a minimal \(\gamma\) is given by

$$\begin{aligned}&P[\text {RMSE}_{k}<\gamma ]=\frac{N_{\text {reg}}}{N_{\text {up}}}, \\&P[\text {RMSE}_{k}<\gamma ]=\frac{N_{\text {irreg}}}{N_{\text {up}}}, \end{aligned}$$

respectively.

Table 5 Report of the proportion of regular and irregular probes configuration, from which the \(\text {RMSE}\) is smaller than a minimum
Full size table

Table5 presents the proportion of probes configuration for which the RMSE is smaller than a minimum in the case of the first scenario (a single synchronous vibration). One observes that in all the cases, there are more irregular probe configuration with smaller RMSE than the regular. For the smallest value of the minimum in the table, only irregular probes’ configuration are presented. This table is in agreement with the general expectation about the required probes arrangement for the identification of the blade vibrating with a single frequency. This statistical analysis in practice enables to guide the experimenter on the choice of the probes configuration.

In the case of the second scenario (simultaneous asynchronous and synchronous vibration), we repeat the optimization process based on the minimization of the \(\text {RMSE}_{k}\), with \(k=1,2,3\), to evaluate the proportion of regularly and irregularly probe configuration for which the amplitudes are predicted with high accuracy.

Table 6 Report of the proportion of regular and irregular probes configuration, from which the \(\text {RMSE}_1\) is smaller than a minimum
Full size table
Table 7 Report of the proportion of regular and irregular probes configuration, from which the \(\text{RMSE}_2\) is smaller than a minimum
Full size table
Table 8 Report of the proportion of regular and irregular probes configuration, from which the \(RMSE_3\) is smaller than a minimum
Full size table

Thus, it is reported in Tables 6, 7, and 8 that mostly all the subsets with probes irregularly spaced are the ones giving better accurate estimation of the amplitudes. This justifies the choice of irregular probe placements to collect data in BTT measurement systems. In addition, it appears on Table 6 a case of a regular spaced probe with the smallest value of the \(\text {RMSE}_1\). In fact, despite the knowledge on the higher probability of irregular probe of obtaining better data collection, a prior analysis as the one presented here is required.

Conclusions

The measurement of blade tip displacement through BTT system is crucial to monitor the blade’s dynamics. To do so, the probes need to be placed adequately to record useful blade tip displacement enabling the the determination of the vibration parameters. This work has proposed a statistical method of determination of the probes arrangement, based on the minimization of the \(\text {RMSE}\) in the case of synchronous vibrations and the combination of synchronous and asynchronous vibrations. In addition, we have shown statistically that in almost all the scenarios considered, the irregular probe placements are the one for which the vibration parameters are obtained with the highest accuracy.