1 Introduction

The topology of the flow around an airfoil at different incidence angles is one of the most important issues in the design studies of aircraft and turbomachines. Particularly, the study of turbulent structures and wake characteristics behind their airfoils is the key to improving the efficiency of these machines. In recent years, many papers have been published on this issue. Some of them focus on investigating the general evolution of turbulence in turbomachines [11, 29, 47]. While others explore the structure of the flow directly around airfoils [17, 27, 30, 42, 48]. Usually, the goal of these studies is to identify the influence of the angle of attack on the turbulence evolution and wake topology.

The behavior of the flow around the streamlined body is a complex phenomenon that includes many factors. One of which is the impact of surface roughness. Even its slight deviation can lead to significant changes in turbulence [40]. According to [52], with increasing level of roughness, the vortex shedding frequency decreases. In addition, the flow deficit behind profiles with a rough surface is much smaller compared to a smooth one [53]. Moreover, the roughness on the suction side of airfoil leads to a greater deficit of velocity contrary on the pressure side. In general, the flow topology around a streamline body and its aerodynamic characteristics is closely related to the phenomena that occur in the boundary layer. For example, the surface tangential and normal stresses determine the magnitude of the drag force [26]. Which is one of the main factors taken into account in aerodynamic design.

Nowadays, much attention is also paid to the study of the anisotropy of turbulent flow. It’s one of the greatest unknown questions in the phenomenology of turbulence, and important in both turbulence theories and turbulent models [31]. Because this phenomenon can change the structure of the flow and determines the characteristics of its formation. In addition, anisotropy indicates the presence of ordered vortices in the turbulent flow. In general, there are several basic theories about anisotropy. Among which it is possible to note the global anisotropy theory, the local anisotropy theory and the return-to-isotropy theory.

Kolmogorov became the founder of the first theory [15, 23]. This theory K41 is based on the idea of isotrophy and homogeneity of turbulent flow. He found, that a quantitative description of small-scale locally isotropic turbulence in the inertial range is based on the use of structure functions and their spectra. Theory K41 describes the energy cascade and estimates isotropic and homogeneous turbulence according to Law \(f^{4/5}\). Also, according to the Kolmogorov law, the spectral density of turbulence energy decreases with the increase of the wave number according to the law of \(f^{-5/3}\) [24].

Monin and Yaglom made a great contribution to the development of K41 theory. They formed the concept of the theory of local isotropy, local stationarity and local homogeneity [34]. In recent decades, a significant amount of research has been devoted to studying the anisotropy of turbulent flow [2, 13, 36, 45]. The obtained results indicate that at a low strain rate the flow anisotropy can be preserved in local structures even at large Reynolds numbers. After that Hill [18], based on the assumption of local homogeneity, proved that the isotropy or anisotropy of turbulent flow does not depend on the law \(f^{4/5}\).

One of the fundamental in the study of turbulent flow anisotropy is the theory of return-to-isotropy [12, 33]. Initially, Lumley and Newman developed this theory for flows with a small or absent main strain rate. But later Choi and Lumley found a way to adapt it for the turbulence without the main strain rate. The authors proposed to place all possible states of turbulence inside the Lumley’s triangle. Generally, it is invariant anisotropy mapping, which is represented by two-dimensional domains based on the invariant properties of the Reynolds stress tensor.

Today, this methodology is widely used in the numerical and experimental analysis of the turbulence flows. In particular, the paper [46] describes the anisotropic flow around the flat plate airfoil. The experimental results indicate that in the general case, the turbulent flow can be divided into two areas. The anisotropic region includes part of the flow in the wake and in the core of the boundary layer. Whereas in other parts of the stream it appears turbulence anisotropy. In addition, there is some tendency to expand the spheroid of the energy ellipsoid, which indicates the presence of a system of vortices with better axis orientation.

Flow anisotropy is a very common phenomenon. The research methodology is similar in many cases. For example, in the paper [43] the authors used the Lemley triangle technique to study in detail the turbulent stress anisotropy tensor in combined wave-current flow. The invariant functions are also presented at a different vertical location from the bed to comprehend the level of anisotropy in the combined flow. The spectral variation of the ratio of momentum flux to the turbulent kinetic energy is examined and discussed in comparison to the canonical value. After that, the Taylor length and Kolmogorov were used to estimate the structure of the turbulent flow.

The methodology described above is also presented for the investigation of turbulence anisotropy through passive grid under rigid boundary influence [41]. Morevor, the paper shows an interesting analysis based on third-order moments of the velocity fluctuations and the ratio of momentum flux to the turbulent kinetic energy in the frequency domain. The obtained results allowed them to conclude that the anisotropic invariant maps possess a closed looping trend in the near field region and an open looping trend in the far-field region of the grid.

Another interesting phenomenon is the effect of flow anisotropy on the distribution of the energy spectrum. For example, this feature is well manifested in the study of the turbulence structure around the FX 63-137 airfoil [44]. The authors conducted an in-depth analysis of the behavior of the Reynolds stress components and the degree of anisotropy around the asymmetric profile. The obtained results allowed to establish that outside the wake region there is a flow zone with a high degree of anisotropy, namely is transition zone. The authors argue that a specific feature of this zone is non typical distribution of the energy spectrum. In particular, in the inertial subrange it has a double slope. This specific pattern became the starting point of our investigation.

In this paper, we will focus on the study of wake topology and the degree of anisotropy of turbulent flow behind the NACA 64-618 airfoil. The organization of the rest parts of the paper is as follows. Materials, methodology of experimental researches and parameters of the measuring equipment are given in Sect. 2. Then the test results are presented in Sect. 3. Firstly, we investigated the distribution of streamwise velocity fluctuations, standard deviation, turbulent kinetic energy and turbulence intensity at various angles of attack and different positions relative to the trailing edge. That allowed us to estimate the wake topology behind the airfoil. This section also discusses anisotropy of turbulent flow based on the analysis of Reynolds stress components. In addition, the structure of the turbulent flow is studied. Then the power spectral density was used to analyze the specific behavior of turbulence in the transit zone. The discussion of the obtained results is presented in Sect. 4. Finally, Sect. 5 reports the conclusion

2 Methodology

2.1 Experimental setup and instrumentations

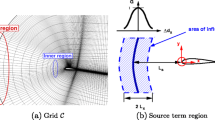
The study of the structure of the turbulent flow behind the asymmetric airfoil was performed in a low-speed open-type wind tunnel. Which was developed at the Department of Energy Systems Engineering, the University of West Bohemia for investigating various flow phenomena (Fig. 1a) [49, 50]. It is should be noted that the special design of the tunnel allows generating flow up 90 \(\mathrm{m}\,\mathrm{s}^{-1}\) with a low degree of turbulence 0.2%. The dimensions of the working space of the test section were 0.3 m, 0.2 m and 0.75 m. Above the test section was placed a travers system. Which provided the movement of the measuring sensor relative to the working space.

The NACA 64-618 airfoil with a chord length of \(c = 80\), span of \(l \cdot c^{-1} \approx 1.5\) and characteristic thickness \(b \cdot c^{-1} \approx 0.18\) was selected for investigation. Accordingly, at these dimensions, the blocking factor was 6%. The airfoil was manufactured of plastic. We used a PRUSA i3 printer and PLA thermoplastic filament for this purpose. After that, using sandpaper P2500, the roughness of the airfoil surface was reduced to 5 \(\upmu \mathrm{m}\).

The position of the airfoil during the experiments is shown in Fig. 1b. Its aerodynamic center was locating at \(\varDelta z \cdot c^{-1} \approx 1.9\) and \(\varDelta x \cdot c^{-1} \approx 2.8\). Where \(\varDelta z\) and \(\varDelta x\) are the distance to the wall and the inlet of the test section, respectively. The distance between the airfoil bottom and test section was \(\varDelta y \cdot c^{-1} \approx 1\).

Generally, measurements were carried out for three angles of attack \(\alpha = +10^{\circ }\), \(0^{\circ }\), \(-10^{\circ }\). While the Reynolds number based on the length of the airfoil chord was \(Re\approx 1.7 \times 10^5\). Which corresponds to the average ambient velocity \(U\approx 32 \;\mathrm{m}\, \mathrm{s}^{-1}\) Two cross-sections at \( x \cdot c^{-1} \approx 0.2\) and \(x \cdot c^{-1} \approx 1.2\) were selected for experimental studies. They were located at a height of \( y \cdot c^{-1} \approx 1.8\).

The Constant Temperature Anemometer and miniature X-wire probe 55P64 were used for the experimental investigation of the turbulent flow. This probe is a good solution for simultaneous investigating the structure of turbulent flow in the streamwise and spanwise directions (u and v components). The wire probes with tungsten platinum coating have a diameter of 5 \(\upmu \mathrm{m}\) and an active length of 1.25 mm. The ends of the wire are gilded with a thickness of 15 \(\upmu \mathrm{m}\) to 20 \(\upmu \mathrm{m}\).

Digitization of the received analog signal from the Dantec Streamline CTA 91C10 module was performed using NI Data Acquisition USB-6364. The flow field measurements were logged at a frequency of 60 kHz. The measurement time at one point was 5 s. After that, the received signal was filtered at high and low frequency. Accordingly, for the high-pass filter at 10 Hz, and for the low-pass filter at 30 kHz.

Fig. 1
figure 1

a Principle construction of the wind tunnel. b Airfoil testing schematic diagram. Where \(z \cdot c^{-1}\) and \(x \cdot c^{-1}\) respectively sizes of the measuring field. Blue arrows indicate the airflow direction

Full size image

2.2 Calibration principle and uncertainty analysis

The basic principle of the constant temperature anemometer is to compensate for the thermal state of the hot-wire [8, 9]. Because when it place in the fluid stream, the heat transfer from the wire to the fluid. The convective heat transfer of wire is principally associated with fluid velocity. Thus, the temperature of the wire changes, which also changes its resistance. The Wheatstone Bridge is used to measure the variation of the resistance of a wire relative to its temperature. In the case of wire cooling, the operating system of the device instantly supplies more energy to the wire. This is necessary to maintain a constant wire temperature. Thus, the power provided to support the system corresponds to the value of the flow rate passing by the sensor.

Collis–Williams law was used to calibrate and estimate the instantaneous flow velocity [21, 35]. Accordingly, the wire cooling in the flow can be described by Eq. 1. Where the left part is responsible for heat transfer, while the right one is the relationship of the King’s law [22].

$$\begin{aligned} N_{c}=Nu\left( \frac{T_{m}}{T} \right) ^{M}=A+BRe_{w}^{N}, \end{aligned}$$
(1)

where the A, B, M, N are calibration constants. It should note, that the first two of them depending on the temperature and dimensions of the wire [3]. The Nusselt number Nu and the wire Reynolds number \(Re_{w}\) can be calculated, as usually e.g. Bruun [10]. While, the \(T_{m}\) is the effective temperature, wich corresponds to relation:

$$\begin{aligned} T_{m}=\frac{1}{2}\left( T_{w}+T \right) \end{aligned}$$
(2)

where T and \(T_{w}\) are the ambient and hot-wire temperature in Kelvins.

Thus, to determine the value for Eq. 1, we performed test measurements at different velocities. Namely, the calibration velocity was from 5 to 42 \(\mathrm{m}\, \mathrm{s}^{-1}\). Then, we were used obtained data to plot a calibration curve of \(Re_{w}\) and \(N_{c}\) (2). After that, the received values were fit with King’s law. This procedure allowed us to find the calibrations constants A, B, M, N. With their help, it is easy to find the wire Reynolds number, which corresponds to the characteristic Nusselt number obtained from the hot-wire signal:

$$\begin{aligned} Re_{w}=\left( \frac{N_{c}-A}{B} \right) ^\frac{1}{N} \end{aligned}$$
(3)

Finally, the instantaneous velocity can be easily determined as follows:

$$\begin{aligned} u=\frac{Re_{w}\nu }{d_{w}} \end{aligned}$$
(4)

where \(d_{w}\) and \(\nu \) are wire diameter and kinematic viscosity of air, respectively.

As we can see from Fig. 2, the obtained calibration curves agree well with the experimental data.

Fig. 2
figure 2

Sample hot-wire blowdown calibration curve for first \(w_{1}\) and second \(w_{2}\) wire. Accordingly, the \(w_{1}\) and \(w_{2}\) are streamwise and span components. The blue line and green dots are the calibration curve and the experimental data, respectively

Full size image

Precision uncertainty of measure velocity was determined using the classical methodologies [14, 20]. Analysis of the obtained data shows, that the general uncertainty of the conversion process of the hot-wire electrical signal to the velocity sample is around \(\pm \,0.5\%\) . This value is approximately equal for measurements in the streamwise and spanwise directions.

3 Experimental results

3.1 Wake topology

The series of experimental studies were conducted to study the characteristics of wake. Firstly, the patterns of mean and standard deviation of streamwise velocity depending on the angle of attack were studied. These parameters were made dimensionless with the average flow velocity of collection data U. For better visualization, the obtained results were placed relative to the trailing edge position at \(\alpha = 0^{\circ }\). Figure 3 shows the effect of the angle of attack on the normalized velocity distribution. Accordingly in cross section at \( x \cdot c^{-1} \approx 0.1\), the largest \( u \cdot U^{-1} \approx 0.55\) and smallest \( u \cdot U^{-1} \approx 0.65\) velocity deficits are observed at \(-10^{\circ }\) and \(0^{\circ }\) , respectively. A similar trend is also observed at \( x \cdot c^{-1} \approx 1.2\). In general, the wave depth with increasing distance by 12 times at \(\alpha = 0^{\circ }, +10^{\circ }\) and \(\alpha = 0^{\circ }\) decreased by 1.3 and 1.6 times, respectively. The wake width has also expanded significantly to almost 2.5 times.

In addition, the experiments clearly show the displacement of the wake center depending on the angle \(\alpha \). This effect occurs due to the difference in flow velocity on airfoil sides. On the suction side, the velocity is higher than on the pressure side, except for the negative angle at which the opposite effect occurs. That is why, the center of the wake near the trailing edge is shifted in the direction of greater pressure, accordingly, lower flow velocity.

The obtained experimental results also show the a slight asymmetry of the wake. This phenomenon follows from the geometry of the airfoil and the angle of its attack. Beside, according to the authors [17, 32], the asymmetric wake expands much faster than symmetric, and produces a higher velocity defect compared with the symmetric ones. This pattern is also observed in our case. For example, in contrast to \(\alpha = +10^{\circ }\) the wake asymmetry and velocity deficit at \(\alpha = -10^{\circ }\) is greater.

Moreover, the maxima of the normalized standard deviation are observed at a positive angle of attack \(\alpha \) (see Fig. 3) This pattern is maintained at different positions of the measuring cross-section. But the behavior of distribution is changing. Namely, the region of maximum values for each angles at \( x \cdot c^{-1} \approx 1.2\) is represented as a plateau. Whereas, closer to the trailing edge at \( x \cdot c^{-1} \approx 0.2\) it transform to double peak. This is one more feature that is caused by the asymmetrical shape of the airfoil. A similar effect was also obtained in the paper [54]. The authors argue that its occurs due to the collision between the upper and lower vortices. Which generated on the suction and pressure side, respectively. This strong interaction leads to a redistribution of the vorticity, which no more concentrates within the core of Karman vortices.

We also found a distribution of turbulent kinetic energy (TKE) and turbulence intensity (TI) in different measuring cross-sections (see Fig. 4). To calculate these parameters, we used classical equations that take into account two components of velocity:

$$\begin{aligned} TKE= & {} \frac{1}{2} \left[ u^{2}- \overline{u^{2}}+\upsilon ^{2}-\overline{\upsilon ^{2}} \right] , \end{aligned}$$
(5)
$$\begin{aligned} TI= & {} \left[ \sqrt{\frac{\overline{{u}'^{2}}+\overline{{\upsilon }'^{2}}}{\overline{{u}^2}+\overline{{\upsilon }^2}}} \right] \cdot 100 \end{aligned}$$
(6)

where the over bar denotes the time-averaging value, u and \(\upsilon \) are the instantaneous velocity of the streamwise and spanwise components, while \(\overline{{u}'^{2}}\) and \(\overline{{\upsilon }'^{2}}\) the represents the mean random components fluctuations to the square.

As a result of the received distributions at \( x \cdot c^{-1} \approx 0.2 \), it is possible to conclude that the maximum of \(TKE \cdot U^{-1}\approx 0.012\) is observed at the positive angle of attack. In contrast to the negative angle where this value is minimal \(TKE \cdot U^{-1}\approx 0.004\). Moreover, with increasing \( x \cdot c^{-1}\) to 1.2, the turbulent kinetic energy decreased 7 times.

Fig. 3
figure 3

Normalized cross-sectoral distributions \(u \cdot U^{-1}\) and \(\sigma \cdot U^{-1}\) at \(Re\approx 1.7 \times 10^5\) depending on the distance \(x \cdot c^{-1}\) and angle \(\alpha \). Green, blue, and light blue indicate the position of the angle of attack \( +10^{\circ }, 0^{\circ }\) and \(-10^{\circ }\), respectively

Full size image

Concurrently, the intensity of the turbulent flow at the wake was investigated. The maximum values of turbulence intensity detected at the \(\alpha = +10^{\circ }\), reaching a value of 22%. It should be noted that this maximum is presented on the pressure side of the wake. Namely at negative values from the wake centerline. The latter corresponds to the position of the trailing edge at \(\alpha = 0^{\circ }\). The obtained results indicate a clear relationship between the turbulent intensity and the wake dimensions. Increasing the turbulence intensity reducing the velocity deficit. A similar relation was also found in the paper [5]. When the authors investigated the effect of turbulence on the wake of a marine current turbine simulator. In our case, as shown in Fig. 3, the largest wake dimensions is observed at \(\alpha = -10^{\circ }\). It should be noted that, at a given angle of attack, the value of IT is higher on the pressure side than on the suction side. Whereas at \(\alpha = +10^{\circ }\) this pattern changes. This phenomenon is explained by the fact that at negative angles the pressure side behaves as the suction side at positive angles.

Fig. 4
figure 4

Distribution of normalized turbulent kinetic energy TKE and turbulence intensity TI at \(Re\approx 170 \times 10^3\) and different \(x \cdot c^{1}\). Green, blue, and light blue indicate the position of the angle of attack \(\alpha = +10^{\circ }, 0^{\circ }\) and \(-10^{\circ }\), respectively

Full size image

3.2 Assessment of Reynolds stress components

The Reynolds stress tensor was used to estimate the nature of the anisotropy of the turbulent flow. Classically, it characterizes the flow relative to three spatial directions x, z and y. But in our case, the 55P64 X-probe allowed us to get information only about two directions (streamwise u and spanwise \(\upsilon \)). As a result, the Reynolds stress tensor was statistically two-dimensional. While its components were normalized to the squared average flow velocity \(U^2\).

Firstly, the analysis of the Reynolds normal stress components depending on the incident angle and position of the measuring probe was performed (see Fig. 5). The distributions of the \(\overline{{u}'^{2}}\) and \( \overline{{\upsilon }'^{2}}\) have similar behavior and varies depending on the angle \(\alpha \). Their maximum values are observed at the positive angle. It should be noted that, close to the trailing edge, the streamwise component in contrast to the spanwise component is characterized by greater instability of the turbulent flow. While with increasing distance this pattern is opposite. For example at \(\alpha = +10^{\circ }\) from \( x \cdot c^{-1} \approx 0.2\) to \( x \cdot c^{-1} \approx 1.2\), the magnitude of \(\overline{{u}'^{2}}\) and \( \overline{{\upsilon }'^{2}}\) decreases by 8.3 and 4.8 times, respectively. In contrast to the position \(\alpha = -10^{\circ }\), where the maximum perturbation decreased by 5 and 7.5 times. This feature shows a significant energy dissipation of vortexes at positive incidence angle. In general, comparative analysis of the normal stress components shows that the vortex on the suction side is dominant.

Fig. 5
figure 5

Normalized distribution of Reynolds stress components \(\overline{{u}'^{2}} \cdot U^{-2}, \overline{{\upsilon }'^{2}} \cdot U^{-2}, \overline{{u}'{\upsilon }'}\cdot U^{-2}\) at \(Re\approx 1.7 \times 10^5\) and different \(x \cdot c^{1}\). Green, blue, and light blue curve indicate the position of the angle of attack \(\alpha = +10^{\circ }, 0^{\circ }\) and \(-10^{\circ }\), respectively

Full size image

The normalized distribution of the Reynolds shear stresses component is shown in Fig. 6. Physically this component related to the diffusion mechanism for transport of fluid momentum. Graphically its shows characteristic distribution asymmetry with the variety of positive and negative symbols through the wake centerline. The obtained distribution of \(\overline{u' \upsilon '}^{2}\cdot U^{-2}\) clearly shows the region of flow instability where the turbulence structure is anisotropic. We can also observe that the area of perturbation with a negative value is located directly on the pressure side. This is explained by the progress of intensity turbulent, which increases the frictional resistance in the mean flow. As a result, turbulence receives energy, and the average flow loses.

The obtained distributions showed that the largest magnitude of the shear component \(\overline{u' \upsilon '}^{2}\cdot U^{-2} \approx 12\) occurs at \(\alpha = +10^{\circ }\) and \( x \cdot c^{-1} \approx 0.2\). While at angles \(\alpha = 0^{\circ }\) and \(\alpha = -10^{\circ }\) its magnitude is 3 and 2 times smaller, respectively. With increasing distance \(x \cdot c^{-1}\) the width of instability region increase and its depth declines. The largest width of this region is observed at \(\alpha = +10^{\circ }\) and \( x \cdot c^{-1} \approx 1.2\). This feature is caused by the presence of a trailing edge, which leads to additional vortex structures that pass through the flow. In general, the Reynolds stress tensor allows us to estimate the isotropy of a turbulent flow characterized by high instability

The comparative analysis of the Reynolds stress tensor and the degree of anisotropy (DA) provides a better understanding of the mechanism of turbulence formation behind an airfoil. In particular, the analysis of DA allows estimating the anisotropy of the flow even with a small instability. According to the methodology described in [44], this analysis is based on the ratio of velocity fluctuations in two directions. To determine DA we used equation:

$$\begin{aligned} DA=\overline{{u}'^{2}} / \overline{{\upsilon }'^{2}} \end{aligned}$$
(7)

where the \(\overline{{u}'}\) and \( \overline{{\upsilon }'}\) time-averaging value of streamwise and spanwise velocity fluctuations, respectively.

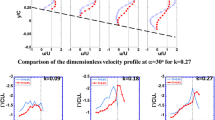
The negative and positive values of DA indicate the dominance of the u and \(\upsilon \) components, respectively. In Fig. 6 shows a comparative analysis of the Reynolds shear stresses and the degree of anisotropy behind the airfoil depending on incident angle and the measuring cross section. The obtained results clearly show the presence of three dominant flow parts. The inner part characterizes the wake region. Its boundaries are determined by the distribution of Reynolds shear stresses and marked by dashed red lines. While the outer part includes a ambient flow that is completely isotropic.

Also, the obtained data clearly show some region between the wake and ambient flow. This region characterizes by low instability and a high degree of flow anisotropy. We can assume that this is a shear layer. Its range is indicated by light green area (see Fig. 6).

Fig. 6
figure 6

Distributions of the normalized Reynolds shear stresses and the degree of anisotropy depending on the \(\alpha \) and distance \(x \cdot c^{-1}\). The boundaries of the wake region are marked with a dashed red line. While green indicates the range of the shear layer. A and B are characteristic points of the turbulent flow

Full size image

Thus, the general region of instability consists of wake region and shear layer. DA analysis also revealed the presence of a double peak. It should be noted that this feature of the distribution is present only within the wake region. Besides, the obtained double peak has some local minimum A. In addition, it corresponds to the position of the inflection point for the Reynolds shear stresses component.

Meanwhile, the distribution of anisotropy in the shear layer has two extremes. Especially this picture is observed at \(\alpha = 0^{\circ }\) and \(\alpha = -10^{\circ }\). Whereas, closer to the wake, the transverse fluctuation starts to be higher than the longitudinal one. While near the stream regions, on the contrary, longitudinal fluctuation predominate. It should be noted that the ratio and distributions of these parameters strongly depend on the angle of attack. For example, at \( x \cdot c^{-1} \approx 0.2\), the highest degree of anisotropy can be observed at \(\alpha = +10^{\circ }\). At this angle the main part of the flow instability is concentrated on the pressure side. Similar patterns also persist with increasing distance from the trailing edge to \( x \cdot c^{-1} \approx 1.2\). But, a significant number of small vortices are generated. They are clearly expressed in the longitudinal direction. Mostly this effect is clearly observed at a negative angle of attack.

Of particular interest for further research are points A and B. Because the first of them characterize the structure of the flow in the center of the wake region. While the second one, reflects the flow features on the boundaries of the wake region and shear layer.

3.3 Length scales analysis of the turbulent flow

Estimation of the turbulent structure is a very useful procedure for identifying the mechanism of flow evolution. This analysis allows to obtain additional information about the scale of coherent structures and to estimate their dissipation characteristics. The main purpose of this section is to determine the characteristics of the turbulent structure in streamwise and spanwise directions.

Detailed methodology for estimating turbulent flow parameters is given in the papers [7, 51]. The experimental studies were performed at the constant distance \( x \cdot c^{-1} \approx 0.2\) and at the different angle of attack \(\alpha \). Namely, it changed from \(+10^{\circ }\) to \(-10^{\circ }\) by \(10^{\circ }\). The characteristic Reynolds number was \(Re\approx 1.7 \times 10^5\). To further estimate the flow, based on the wake topology, we chose the range \(z \cdot c^{-1}\) from \( -0.4\) to 0.4

Initially, a correlation analysis was performed to estimate the temporal and spatial scales of the vortices. The lifetime of vortices can be found from the Euler autocorrelation distribution. Accordingly, the place where its value becomes zero corresponds to the lifetime of the largest vortices. Euler’s autocorrelation function of the streamwise components can be found by Eq. . While for the spanwise component, it calculates similarly.

$$\begin{aligned} R_{uu}=\frac{ \overline{{u}\left( {t+\varDelta {t}} \right) } \cdot \overline{{u}\left( {t} \right) }}{\sigma _{u}^{2}}, \end{aligned}$$
(8)

where u is the streamwise component of velocity fluctuation and the overbar indicate the average value. While \(\sigma _{u}^{2}\) and \(\varDelta {t}\) are the variance of velocity components and the shift time of the measuring signal, respectively.

Then, using the cumulative integral, we determined the average lifetime of the vortices T:

$$\begin{aligned} T=\int _{0}^{\infty }R_{uu}\left( {t}'\right) d{t}' \end{aligned}$$
(9)

After that, the integral Eulerian length scale T of the flow can be easily calculated by the ratio:

$$\begin{aligned} L=T / \sigma \end{aligned}$$
(10)

It should be noted that T characterizes the average size of vortices.

Then, using the second-order Euler structural function \(S_{uu}\), we determined the dissipation rate \(\epsilon \). Mathematically, the degree n of the \(S_{uu}\) is the moment of the probability density function of the velocity increments \(S_{uu}^{n}=\left[ u\left( t+\varDelta {t} \right) -u\left( t \right) \right] ^{n}\). From a physical point of view, the \(S_{uu}^{2}\left( t\right) \) describes the inertial characteristics of the turbulence. According to Kolmogorov’s papers at large Reynolds numbers, the second-order structure function can be found as:

$$\begin{aligned} S_{uu}^{2}\left( t\right) =2.1\left( \epsilon \cdot t \right) ^{2/3} \end{aligned}$$
(11)

where 2.1 is empirically known to be approximately [4].

Finally, value of dissipation \(\epsilon \) we found from the plateau of cumulative integral of structure function.

Once the rate of dissipation is known, the Kolmogorov microscale \(\eta \) and Taylor micro-scale \(\lambda \) of the turbulent flow are estimated from classical relations:

$$\begin{aligned} \eta =\left( \nu ^{3}/\epsilon \right) ^{1/4}, \end{aligned}$$
(12)
$$\begin{aligned} \lambda =\sigma \sqrt{15\nu /\epsilon } \end{aligned}$$
(13)

where \(\nu \) is kinematic viscosity of air,

Graphical interpretations of the obtained data are shown in Fig. 7. As we can see, the maximum values of integral length scale for the streamwise component \(T_{u} \approx 2.5{mm}\) and spanwise component \(T_{\upsilon } \approx 1.5{mm}\) are observed at \(\alpha = +10^{\circ }\).

While their minimums occur at at the \(\alpha = -10^{\circ }\). In general, a sharp increase of the vortex dimensions is observing in the wake area. Namely, at \(0^{\circ }\)and \(+10^{\circ }\) it phenomenon occurs from the pressure side, but at \(-10^{\circ }\) on the contrary side. The biggest difference between the magnitude of vortices is observed at \(\alpha = 0^{\circ }\). Accordingly, their ratio relative streamwise and spanwise directions are \(T_{u} / T_{\upsilon } \approx 3.3\). The analysis of the obtained data also exposed some specifics of the transit zone. Namely, the dominance of the streamwise component, regardless of the angle of attack.

However, estimating the distribution of Kolmogorov microscales, a different pattern is observed. The dimensions of the smallest eddies in streamwise and spanwise directions are almost identical. In the wake region, they have the lowest values \(\eta \approx 28\,{\upmu \mathrm{m}}\) regardless of \(\alpha \). Whereas the maximum value of the \(\eta \) is observed in the shear layer and strongly depends on the angle of attack. In addition, based on previous studies (see Fig. 6 ), we can observe a clear relationship between the behavior of the flow anisotropy and the distribution of Kolmogorov microscales. Similar to DA, the greater value of \(\eta \approx 90\,{\upmu \mathrm{m}}\) is observed at \(\alpha = +10^{\circ }\).

The Taylor micro-scale distribution showed that its highest values, regardless of the angle of attack, are placed in the wake range. Whereas starting from the B point, this parameter decreases sharply. For example, at \(\alpha = +10^{\circ }\) the magnitude of \(\lambda _{u}\) and \(\lambda _{\upsilon }\) decreased to 12 and 9 times, respectively. Besides, you can detect the double peaks in the shape of the curves. Its local minimum corresponds to the point A. Which, as noted earlier, reflects inflections of Reynolds shear stress distribution.

Interesting patterns also showed the distributions of dissipation rate. In the general case, inside the wake region, there is a significant dominance of the spanwise component in the flow. For example, the difference between the maximum values of \(\epsilon _{\upsilon }\) and \(\epsilon _{u}\) depending on \(\alpha \) is: at \(0^{\circ } \approx 1.4\) times, at \(+10^{\circ } \approx 1.6\) times and at \(-10^{\circ } \approx 1.2\) times. Moreover, these maxima locate from the pressure side. While within the shear layer, the dissipation rate has decreased sharply.

In general, the structure of the turbulent flow has its distribution features depending on the flow region. Thus, in the wake region, a significant flow perturbation is observed. Wich in the shear layer sharply decreases to parameters of the general flow. Interesting is the fact that, at points A and B, most of the turbulence parameters in streamwise and spanwise directions are similar. This feature may indicate the presence of stable large-scale coherent structures in the turbulent flow.

Fig. 7
figure 7

Comparison the flow characteristics in streamwise and spanwise directions depending on the angle of attack \(\alpha \) at \( x \cdot c^{-1} \approx 0.2\). While the u and \({\upsilon }\) are streamwise and spanwise component, respectively. The green color indicates the range of the shear layer. Meanwhile, the blue and red dashed lines indicate the positions of points A and B, respectively

Full size image

3.4 Power and dissipation spectrum

The turbulent flow is a complex phenomenon whose evolution is associated with the peculiarities of the interaction of different spatial scales. Thus, in a homogeneous turbulent flow, there are fluctuations in a wide range. The large-scale fluctuations contain the bulk of the energy of the turbulent flow and play a significant role in the subsequent formation of vortices. While small-scale fluctuations correspond to large wavenumbers and are responsible for the dissipation of energy into heat. In addition, according to Kolmogorov’s theory, at large Reynolds numbers [12, 24], there is the inertial subrange where energy is not produced and dissipated but transmitted to higher wavenumbers.

Fig. 8
figure 8

Normalized Eulerian power spectral densities of straemwise and spanwise fluctuations depending on the angle of attack at \(x \cdot c^{-1} \approx 0.2\) and \(Re \approx 1.7 \cdot 10^5\). Green and blue color indicates the spectral density for measuring points A and B, respectively

Full size image
Fig. 9
figure 9

Normalized dissipation spectral of straemwise and spanwise fluctuations depending on the angle of attack at \(x \cdot c^{-1} \approx 0.2\) and \(Re \approx 1.7 \times 10^5\). Green and blue color indicates the spectral density for measuring points A and B, respectively

Full size image

The spectral power density was used to estimate the features of the flow energy distribution between different turbulence scales. Based on the Fourier spectral analysis, the quantitative of turbulent flow energy was determined. To spectrally estimate the turbulent flow, we also chose points A and B. They were located behind the trailing edge at \( x \cdot c^{-1} \approx 0.2\) and \( y \cdot c^{-1} \approx 1.8\). As mentioned earlier, the first point corresponds to the minimum flow velocity and the inflection position of the Reynolds shear stresses distribution. The second point is placed on the boundary of the wake region and the shear layer. As the angle of attack changes, the coordinates of the measuring points vary slightly. Accordingly, for the A point the \( z \cdot c^{-1}\) was: at \(\alpha = 0^{\circ } \approx 0.05\) , at \(\alpha = +10^{\circ } \approx -0.09\) and at \(\alpha = -10^{\circ } \approx 0.17\) . While for B point, the \( z \cdot c^{-1}\) position corresponds: at \(\alpha = 0^{\circ } \approx 0.13\) , at \(\alpha = +10^{\circ } \approx 0.04\) and at \(\alpha = -10^{\circ } \approx 0.21\) .

Graphical interpretation normalized Eulerian power spectral densities of velocity fluctuations depending on the angle \(\alpha \) shown in Fig. 8. For representing the data non-dimensional coordinates were used. The obtained spectrum \(E\left( k \right) \) was normalized by \(\left( \eta \cdot \nu ^{5} \right) ^{1/4}\) and the wave number as \(\textit{k} \cdot \eta \). Where \(\eta \), \(\epsilon \) and \(\nu \) is dissipation scale, dissipation rate and viscosity, respectively. These parameters are determined according to the methodology outlined above (see Sect. 3.3). The obtained distribution clearly shows the inertial subrange from \(k\approx L^{-1}\) to \(k\approx \eta ^{-1}\) in streamwise and spanwise directions for both measuring points. According to the results, the largest and smallest width of it observed at \(\alpha =0^{\circ }\) and \(\alpha =+10^{\circ }\), respectively. At these angles of attack, the energy-containing eddies are one order of magnitude lower for point B than for point A. Besides, at \(\alpha =-10^{\circ }\), this difference increases twice.

In general, is some clear difference in the feature of the spectrum distribution between B and A points. In the first case, the inertial subrange has a characteristic slope of curve \(f^{- 5/3}\). It indicates that the turbulent flow is locally homogeneous and isotropic and stays in statistical equilibrium in longitudinal and transverse directions. That is confirmed in the previous section (see Fig. 6). Meanwhile, at point B, the spectral distribution curve has a double slope \(f^{-3}\) after that \(f^{- 5/3}\). This trend is present at different angles of attack and can be observed only on the boundaries of the wake region.

Besides, at \(\alpha = -10^{\circ }\), the spectrum distributions at the M point have clearly expressed peaks. Their appearance is observed at about 3.2 kHz. Moreover, the magnitude of these peaks is three times higher than at point A. It should be noted that their location corresponds to the place where the curve changes its slope.

Finally the dissipation spectrum for the measuring points A and B was estimated (Fig. 9). The dissipation phenomenon occurs at high wavenumbers where the smallest vortices dissipate turbulent energy due to viscosity. Thus, the dissipation spectrum can to obtained from the power spectrum by simply multiplying with the square of the wavenumber:

$$\begin{aligned} D\left( k \right) = 2 \nu k^{2}E\left( k \right) \end{aligned}$$
(14)

For non-dimensional coordinates, we used normalization in the form \(D\left( k \right) / \eta \cdot \epsilon \) and for wave number \(\textit{k}\cdot \eta \).

Again, the distribution of the dissipation spectrum for point A in the inertial range has a classical form. Namely, its curve has a slope of \(f^{1/3}\). A similar result for homogeneous isotropic turbulence was obtained by Pope [37]. But for point B in the region of large wavenumbers at \(k\approx L^{-1}\), there is some convexity. After that, the curve again has a slope of \(f^{1/3}\). This feature detects only at B point where the turbulent flow has a high degree of anisotropy.

Thus, we can conclude that the dissipation and power spectrums are strongly dependent on the flow anisotropy, and their distributions may indicate the start of the shear layer.

4 Discussion

This section is devoted to the discussion about the double slope of the spectral distribution at point B. As mentioned earlier, its position indicates the beginning of the shear layer. Which is characterized by a high degree of flow anisotropy.

As is known, the main sign of turbulence is the chaotic nature of variations in the thermodynamic characteristics of the flow in space and time. Moreover, in the fully developed turbulence, the energy externally injected is redistributed among length scales due to non-linear eddy interactions. Thus, the spectral energy density in the inertial range of locally isotropic turbulence is determined only by the dissipation rate [24]. After that, kinetic energy is transfer into heat at a small scale. This description is valid at some boundary conditions. Namely, if the only energy supply is a vortex, which appears due to the instability of the main flow, and the only sink of energy is its transition to the heat due to dissipation. In our case, this scenario can be observed at the A point (see Fig. 8 ). There, the spectral energy distribution has a characteristic shape with a slope of \(f^{-5/3}\).

But for some cases of turbulence, other sources and sinks of energy could exist. They lead to a completely different evolution of the turbulent flow. In the presence of such processes as rotation, stratification, confinement, and shear, the direction of the energy cascade undergoes significant changes [1]. For example, in the 2D homogeneous isotropic turbulence. That is a truly paradigmatic example there presents the split energy cascade. This phenomenon was predicted in a series of fundamental works by Kraichnan, Leith and Batchelor [25, 28]. Accordingly to theory, an inverse inertial range dominated by the energy flux and a direct inertial range dominated the enstrophy flux lead to the definition of two cut-off scales. Thus, from large and small-scale sides of energy injection, the spectral distribution is characterized by slopes \(f^{-5/3}\) and \(f^{-3}\), respectively.

At the same time, some papers proposed an opposite scenario. Thus, the authors [15] claim that, in contrast to Kraichnan theory, the spectrum \(f^{-5/3}\) occurs on the short-wave side (large k). Accordingly to [6], researchers also found that the spectrum distribution in the inverse energy cascade range deviates from the \(f^{-5/3}\) slope and becomes closer to \(f^{-3}\). The reason for the deviation is traced to the emergence of strong vortices distributed over all scales.

The effect of rotation is likewise of considerable interest. Because under some boundary conditions, this phenomenon increases the degree of turbulence anisotropy, [16]. Besides, in the presence of intensive rotation, the flow becomes quasi-two-dimensional (the Taylor-Proudman theorem [19, 38]). This feature greatly changes the evolution of the energy cascade, which also may contain an anisotropic part of energy transfer [1].

This phenomenon became the starting point for understanding the causes of the double energy cascade at measuring point B. Thus, based on the above analysis and our experimental data, we can make assumptions. In the shear layer of the wake region, there are arise stable quasi-2D coherent structures. Some of them accelerate due to interaction with an ambient flow. That leads to an escalation of turbulence anisotropy. It should note, that investigation of vortical structures in the mixing layer revealed a similar scenario [39]. After that, the new coherent structures merge and, as a consequence, increase their strength. Thus reverse enstrophy cascade with a slope of \(f^{-3}\) occurs in the energy cascade at a large scale (small k). Of course, this is only the hypothesis and needs further exploration.

5 Conclusion

This experimental study assessed the turbulence structures and the anisotropic behavior behind NACA 64-618 airfoil. Using hot-wire anemometry with miniature X-wire probe 55P63, a series of graphical distributions of velocity, turbulent kinetic energy, turbulence intensity and standard deviation profiles in different measuring sections were obtained. The results allow us to carefully analyze the wake topology. We found that, the center of the wake is characterized by a sharp deficit of velocity. Its position strongly depends on the angle of attack and shifts in the transverse direction. The normal Reynolds stress components were also used to assess the wake parameters. Their maximum magnitude observes at a positive angle of attack. Moreover, the obtained graphical distributions reflect the double-peaked in the instability zone. This phenomenon is due to the interaction of vortices formed from different airfoil sides. While the Reynolds shear stress component shows a region of flow instability, where the turbulence structure is isotropic. Also, based on the compare analysis of the flow anisotropy and shear stress distribution, we found clear boundaries of the shear layer. In addition, we carefully studied the turbulent structure behind the airfoil. Interesting patterns also showed the distributions of dissipation rate. Inside the wake region, there is a significant dominance of the span-wise component in the flow. Besides, we performed a spectral analysis of the flow energy distribution at the two measuring points. The first of them was placed in the wake, while the other was in the shear layer. We found that that the energy cascade of turbulent flow in the shear layer has a double slope \(f^{-3}\) after that \(f^{-5/3}\). This behavior is observed at different angles of attack. Based on the analysis, we assumed that this feature could be arises as a result of the reverse enstrophy cascade of the vortex merging.