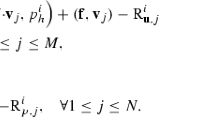Krylov improvements of the Uzawa method for Stokes type operator matrices

Abstract

The paper is devoted to Krylov type modifications of the Uzawa method on the operator level for the Stokes problem in order to accelerate convergence. First block preconditioners and their effect on convergence are studied. Then it is shown that a Krylov–Uzawa iteration produces superlinear convergence on smooth domains, and estimation is given on its speed.

1 Introduction

The Stokes problem:

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta \mathbf{u}+ \nabla p = \mathbf{f}\\ \ \mathop {div}\mathbf{u}= 0 \\ \ \mathbf{u}_{\mid \partial \Omega } = 0 \, \end{array} \right. \end{aligned}$$

(1.1)

in bounded domains $\Omega \subset \mathbf{R}^d$ is constantly in the focus of interest due to its basic role in fluid modelling, either on its own or as a building block for more elaborate models, and it also serves as a principal model for a saddle-point problem. Iterative methods for its solution have also been studied up to recently, see, e.g., [9, 13, 19, 28] and the references there. To name two major approaches, Uzawa type methods or MINRES-based iterations are of great interest, and various linear convergence estimates have been proved.

This paper is concerned with the Uzawa approach. In this context one often studies the iteration on a function space level for the operators themselves, see, e.g., [10, 25, 28], since this provides a more direct insight into the structure of the problem and also indicates the asymptotic behaviour of the iterations on proper sufficiently fine meshes. We also follow this vein. Furthermore, we address the Krylov type modification of the Uzawa method. Namely, in spite of the simplicity and elegance of the Uzawa method, which arises from a simple iteration applied to the Schur complement problem, it might be recommended to replace the simple iteration by the conjugate gradient (CG) algorithm to accelerate convergence [30].

Our paper considers first block preconditioners for operator matrices arising in the context of the Stokes problem, and studies their effect on convergence related to Krylov iterations. The need to use regularization is pointed out, and improvements are discussed for the Uzawa method, which is a basic defect-correction process, by use of a Krylov subspace iterative acceleration method. The discussion is given on a general operator level, which also covers the case of matrices arising from a finite element discretization.

Moreover, involving the conjugate gradient approach opens the way to study possible superlinear convergence, which is a typical phenomenon for Krylov methods in certain situations. Superlinear convergence of CG type methods has been derived for proper operators in Hilbert space, see, e.g., [23, 31] and the authors’ papers [6, 7] which also cover certain elliptic operators. However, to the authors’ knowledge, for the Stokes problem no superlinear result has been given yet. In the closing section of the paper we study an Uzawa-related iteration which comes from the CG method applied to the Schur complement problem on the operator level. We prove superlinear convergence in the case of smooth domains, furthermore, we give an estimate on its speed.

The paper starts with the properties of the Stokes problem and the involved iterations in Sects. 2 and 3, then the above-mentioned results are presented in Sects. 4 and 3.2, respectively.

2 Properties of the Stokes problem

2.1 The operator matrix

The Stokes problem can be written in an operator matrix form, moreover, it is a prototype of such saddle-point problems. Let us define the space

$$\begin{aligned} L^2_0(\Omega ):=\{ p\in L^2(\Omega ): \ {\int \limits _\Omega p=0}\} \end{aligned}$$

(2.1)

and the operators

$$\begin{aligned} L:=-\Delta : \ H^1_0(\Omega )^d\rightarrow H^{-1}(\Omega )^d, \qquad B:=-\mathop {div}: H^1_0(\Omega )^d\rightarrow L^2_0(\Omega ),\ \end{aligned}$$

(2.2)

where the Laplacian acts coordinatewise and includes zero Dirichlet boundary conditions. Then, as is well-known, the adjoint of B is $B^*=\nabla$, hence, changing the sign of the second row of (1.1), we can altogether rewrite it as the system

$$\begin{aligned} \begin{bmatrix} L &{} B^*\\ B &{} 0 \end{bmatrix} \begin{bmatrix} \mathbf {u} \\ {p} \end{bmatrix} = \begin{bmatrix} {f} \\ {0} \end{bmatrix}\, . \end{aligned}$$

(2.3)

It is also well-known that the linear operators L and B in the setting of (2.2) are bounded. In the sequel we will sometimes consider the general operator form (2.3) instead of (1.1), which also covers the special case when L and B are proper matrices (arising from a finite element discretization), see Section 4.

2.2 The Schur complement operator

The basis of both the well-posedness and certain iterative solutions of the problem are the well-known facts summarized below. By eliminating $\mathbf{u}$, the Stokes system can be recast to the single equation

$$\begin{aligned} Sp=\tilde{f} \qquad \text{ in } \ \, L^2_0(\Omega ), \end{aligned}$$

(2.4)

where

$$\begin{aligned} Sp:=\mathrm{div}\,\Delta ^{-1}\nabla p \end{aligned}$$

(2.5)

and $\tilde{f}:= \mathrm{div}\,\Delta ^{-1}\mathbf{f}$. Here both the operators $\nabla$ and $\Delta$ are understood in weak form, in fact $L=-\Delta$ and $\nabla =B^*$ in accordance with (2.2).

The operator $S:L^2_0(\Omega )\rightarrow L^2_0(\Omega )$ will be called ’Schur complement operator’. In fact, it plays the same role as the Schur complement matrix for saddle-point matrices in analogy with (1.1). The well-posedness of equation (2.4) is due to the fact that S is a bounded coercive self-adjoint operator: in fact,

$$\begin{aligned} \gamma ^2 \Vert p\Vert _{L^2}^2\le \langle Sp,p\rangle _{L^2}\le \Vert p\Vert _{L^2}^2 \qquad (\forall p\in L^2_0(\Omega )), \end{aligned}$$

(2.6)

where $\gamma >0$ is the inf-sup constant on $\Omega$. For a further discussion on inf-sup constants, see subsection 4.1.2.

The eigenvalues of the Schur complement operator have been studied in various situations [18, 29, 32]. The definition (2.5) implies that an equation $Sp=\lambda p$ can be reformulated as

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta \mathbf{u}+ \nabla p = \mathbf{0}\\ \ \mathop {div}\mathbf{u}= \lambda p \end{array} \right. \end{aligned}$$

together with the Dirichlet boundary conditions. Eliminating p yields

$$\begin{aligned} -\lambda \, \Delta \mathbf{u}+ \nabla \mathop {div}\mathbf{u}= \mathbf{0}, \end{aligned}$$

that is, the problem can thus be related to the Cosserat spectrum [29].

Later we will need a result from [18]. Therein the action of S is described on the following subspaces of $L^2_0(\Omega )$:

$$\begin{aligned} N:= \{ p\in L^2_0(\Omega ): \ \exists z \ \text{ such } \text{ that } \ \Delta z=p \ \text{ and } \ \nabla z \in H^1_0(\Omega )^d \}, \quad M:=N^\bot \ \text{ in } \ L^2_0(\Omega ). \end{aligned}$$

Theorem 2.1

[18] We have $S_{|N}= I$. Further, if $\partial \Omega \in C^3$, then S on M can be decomposed as  

$$\begin{aligned} S_{|M}=\frac{1}{2}I+K \end{aligned}$$

for some compact operator $K:M\rightarrow M$; in fact, K maps M continuously into $H^1(\Omega )$.

3 Background on iterative methods

3.1 Uzawa and Krylov–Uzawa iterations

Uzawa iteration A popular way to solve the Stokes problem is the Uzawa iteration, which is still in the focus of recent interest, see, e.g., [16, 20, 24]. On the continuous level and in strong form, it reads as

$$\begin{aligned} \begin{array}{l} -\Delta \mathbf{u}_{k+1} + \nabla p_k = \mathbf{f}, \qquad \mathbf{u}_{k+1\, \mid \partial \Omega } = 0 \\ \ \ \text{ and }\qquad p_{k+1}= p_{k} -\alpha \mathop {div}\mathbf{u}_{k+1}\, \end{array} \end{aligned}$$

(3.1)

starting from an arbitrary $p_0\in L^2_0(\Omega )$.

This iteration is equivalent to a simple iteration applied to equation (2.4) in $L^2_0(\Omega )$. Namely, the sequence

$$\begin{aligned} p_{k+1}:= p_{k} -\alpha \, (Sp_k - \tilde{f}) \end{aligned}$$

can be rewritten with the auxiliary variable $\mathbf{u}_{k+1}:= \Delta ^{-1}(\nabla p_k-\mathbf{f})$ to yield (3.1). Consequently, due to the spectral bounds in (2.6), the optimal parameter is $\alpha := \frac{2}{1+\gamma ^2}$ and the corresponding optimal convergence factor is $\frac{1-\gamma ^2}{1+\gamma ^2}$, where $\gamma >0$ is the inf-sup constant on $\Omega$. For further solid details on the Uzawa method, see, e.g., [10, 28].

Krylov–Uzawa iteration In spite of the simplicity and elegance of the Uzawa method, if $\gamma$ is small then it may be recommended to replace the simple iteration by the CG algorithm for (2.4), see [30], and also [1, 12, 27] for similar ideas. That is, for arbitrary $p_0\in L^2_0(\Omega )$,

we let $d_0=r_0:=Sp_0 - \tilde{f}$, and if $p_k$, $r_k$ and $d_k$ are found, then

$$\begin{aligned}&p_{k+1} := p_k + \alpha _k \, d_k , \qquad r_{k+1} := r_k + \alpha _k S \, d_k , \quad \hbox {\ where } \alpha _k := \frac{\Vert r_k\Vert _{L^2}^2}{\langle S\, d_k, d_k \rangle _{L^2}}\, ; \qquad \end{aligned}$$

(3.2)

$$\begin{aligned}&d_{k+1} := r_{k+1} + \beta _{k} d_{k}, \quad \hbox {\ where } \beta _k := \frac{ \Vert r_{k+1}\Vert _{L^2}^2}{\Vert r_k\Vert _{L^2}^2}. \end{aligned}$$

(3.3)

We then obtain the Krylov–Uzawa iteration by rewriting (3.2)–(3.3) in the same manner as above in the Uzawa case, using again the auxiliary variable $\mathbf{u}_{k+1}:= \Delta ^{-1}(\nabla p_k-\mathbf{f})$ and also introducing $\mathbf{z}_{k}:= \Delta ^{-1}\nabla d_k$. Thus, given $p_0\in L^2(\Omega )$, we first let $d_0=r_0=\mathrm{div}\,\mathbf{u}_0$ where $\mathbf{u}_0$ solves $-\Delta \mathbf{u}_0 + \nabla p_0 = \mathbf{f}$, $\mathbf{u}_{0\, \mid \partial \Omega } = 0$. Further, if $p_k$, $\mathbf{u}_k$, $r_k$ and $d_k$ are found, then the next iterates are determined as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \ p_{k+1} := p_k + \alpha _k \, d_k , \\ \ \text{ solve } \ -\Delta \mathbf{z}_k + \nabla d_k = 0, \quad \ \mathbf{z}_{k\, \mid \partial \Omega } = 0 \, , \\ \ \mathbf{u}_{k+1}:=\mathbf{u}_k + \alpha _k \, \mathbf{z}_k ,\\ \ r_{k+1}:=r_k + \alpha _k \, \mathrm{div}\,\mathbf{z}_k ,\\ \ d_{k+1} = r_{k+1} + \beta _{k} d_{k}\, . \end{array} \right. \end{aligned}$$

(3.4)

The constants $\alpha _k$ and $\beta _k$ are as in (3.2)–(3.3), except that $S d_k$ in $\alpha _k$ is replaced by $\mathrm{div}\,\mathbf{z}_k$.

Compared to the Uzawa iteration, the main cost of a Krylov–Uzawa step is similarly the solution of an auxiliary Poisson equation, but additional work is needed to compute the search directions and the inner products in $\alpha _k$ and $\beta _k$. On the other hand, the convergence factor of linear iteration is now $\frac{1-\gamma }{1+\gamma }$.

Moreover, in contrast to a simple iteration, superlinear convergence may arise in Krylov iterations under proper circumstances.

The last section of this paper will be devoted to superlinear convergence estimates in Krylov–Uzawa context.

We note that the actual realizations of Uzawa and Krylov–Uzawa iterations involve approximate solution of the Poisson equations, mostly using inner iterations, which has to be executed to high accuracy to control the overall error. In particular, realizing superlinear convergence needs an increasing inner accuracy. This situation is similar to inexact Newton methods for nonlinear problems.

3.2 Superlinear convergence of Krylov iterations

In this section we briefly summarize some well-known facts on the conjugate gradient (CG) algorithm. (For detailed discussions on CG methods, see e.g. [2].) The basic properties hold not only in $\mathbf{R}^n$ but also on a Hilbert space level (see also [31]), which we address in this paper. Therefore, let us consider a bounded linear operator $A:H\rightarrow H$ in a Hilbert space H, and a linear equation

$$\begin{aligned} Ax = b \end{aligned}$$

(3.5)

for a given $b\in H$. We assume that A is self-adjoint and coercive, hence (3.5) is well-posed.

The CG iteration has been recalled in (3.3) for equation $Sp=\tilde{f}$, now we consider its analogue for (3.5). In the study of convergence, one considers the error vector

$$\begin{aligned} e_k =x-x_k \end{aligned}$$

(3.6)

and is in general interested in its energy norm

$$\begin{aligned} \Vert e_k\Vert _A=\langle Ae_k,e_k\rangle ^{1/2} . \end{aligned}$$

(3.7)

The convergence estimates rely on the optimality property

$$\begin{aligned} \Vert e_k\Vert _A = \min \limits _{P_k\in \pi ^1_k} \Vert P_k(A)e_0 \Vert _A \, . \end{aligned}$$

(3.8)

In particular, if A has a complete eigensystem (which alway holds in the finite dimensional case), then (3.8) implies

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A} \le \min \limits _{P_k\in \pi ^1_k} \max _{\lambda _i\in \sigma (A)} |P_k(\lambda _i)|\, , \end{aligned}$$

(3.9)

where $\lambda _i$ ($i\in \mathbb {N}$) are the eigenvalues of A. This is the basis of superlinear estimates.

3.2.1 Compact perturbations of the identity

The well-known superlinear convergence rates for the CG can be proved for compact perturbations of the identity, that is, if the decomposition

$$\begin{aligned} A=I+E \end{aligned}$$

(3.10)

holds, where I is the identity and E is a compact operator in H. We recall the derivation for use below, based on [2]. Note that this was established on Hilbert space level in [31]. Since E is also self-adjoint, A has a complete eigensystem (the same as E). Let us denote the eigenvalues of A and E by $\lambda _j(A)$ and $\mu _j(E)$, or briefly, just by $\lambda _j$ and $\mu _j$, respectively, ordered according to $|\mu _1|\ge |\mu _2| \ge ...$. Here $\lambda _j=1+\mu _j$. Let us choose $P_k(\lambda ):= \prod _{j=1}^k \bigl ( 1- \frac{\lambda }{\lambda _j}\bigl )$ in (3.9), Since $P_k (\lambda _i) = 0$   ($i = 1,\ldots ,k$), and using that $|\mu _j - \mu _i| \le 2|\mu _j|$   ($i \ge k+1$,   $1\le j \le k$) and ${1\over \lambda _j}\le \Vert A^{-1}\Vert$, we obtain

$$\begin{aligned} \max _{\lambda _i\in \sigma (A)} |P_k(\lambda _i)| = \max _{i\ge k+1} |P_k (\lambda _i)| = \max _{i\ge k+1} \prod _{j=1}^k \frac{|\mu _j-\mu _i|}{ \lambda _j} \le \bigl ({2\Vert A^{-1}\Vert }\bigr )^k \prod _{j=1}^k |\mu _j |\, . \end{aligned}$$

(3.11)

Using (3.9) and the arithmetic-geometric means inequality, we finally find that

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A}\right) ^{1/k} \le \ \frac{2\Vert A^{-1}\Vert }{ k } \ \, \sum \limits _{j=1}^k \bigl | \mu _j(E) \bigr | \qquad (k=1,2,... ). \end{aligned}$$

(3.12)

Here $\mu _j(E)\rightarrow 0$ and hence its arithmetic means $\frac{1}{ k } \sum _{j=1}^k \bigl | \mu _j(E) \bigr |\rightarrow 0$ as well, that is, we obtain a superlinear convergence rate.

3.2.2 Compact perturbations of algebraic operators

Now we extend the above superlinear estimate for decompositions where the identity operator in (3.10) is replaced by an algebraic operator. A related qualitative result has been given in [21], however, we need an estimation in a quantitative form. We derive a new result analogous to (3.12).

An algebraic operator J is the root of a nonzero polynomial, and in this case the space H is the direct sum of subspaces $ker(J-\sigma _{\ell } I)^{r_\ell }$. For us it suffices to assume that $\sigma _\ell$ are single roots, i.e. all $r_\ell =1$ and $\sigma _\ell$ are eigenvalues. That is, we can formulate the following result.

Theorem 3.1

Let the bounded linear operator $A:H\rightarrow H$ admit the decomposition

$$\begin{aligned} A=J+E , \end{aligned}$$

where:

• (i) $J:H\rightarrow H$ has eigenvalues $\sigma _1, \dots , \sigma _s>0$ and the eigenspaces $H_\ell$ of $\sigma _\ell$ span H, i.e. $H=H_1\oplus \dots \oplus H_s$;

• (ii) $E:H\rightarrow H$ is compact self-adjoint and $H_\ell$ ($\ell =1,...,s$) are invariant subspaces for E.

Then the error vectors of the CG algorithm for (3.5) satisfy

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A}\right) ^{1/k} \le \ C \cdot \Bigl ( \frac{1}{ \lfloor \frac{k}{s} \rfloor } \, \sum \limits _{j=1}^{\lfloor \frac{k}{s} \rfloor } \max _{\ell =1,...,s} \bigl | \mu _j(E_{| H_\ell }) \bigr | \Bigr )^{1/s} \rightarrow 0 \qquad (\text{ as } \ k\rightarrow \infty ) \end{aligned}$$

(3.13)

for some constant $C>0$ independent of k.

Proof

The assumptions imply that

$$\begin{aligned} A_{| H_\ell }=\sigma _\ell I_{| H_\ell } + E_\ell \end{aligned}$$

(3.14)

where $E_\ell : = E_{| H_\ell }:H_\ell \rightarrow H_\ell$ are compact self-adjoint ($\ell =1,...,s$), further, that the eigenvalues of A are

$$\begin{aligned} \lambda _{\ell j}:= & {} \lambda _{\ell j}(A) = \sigma _\ell \nonumber \\&+ \mu _j (E_\ell ) \quad (\ell =1,\dots ,s; \ j=1,2,\dots ), \end{aligned}$$

(3.15)

where $\mu _j (E_\ell )$ ($j\in \mathbb {N}^+$) denote the ordered eigenvalues of $E_\ell$, that is, $|\mu _1(E_\ell )|\ge |\mu _2(E_\ell )| \ge ...$. Here for all fixed $\ell$ we have $\mu _j (E_\ell )\rightarrow 0$ as $j\rightarrow \infty$. The operators $A_{| H_\ell }=\sigma _\ell I_{| H_\ell } + E_\ell$ have complete eigensystems in $H_\ell$ for all fixed $\ell =1,\dots ,s$, hence, using their union, A has a complete eigensystem in H. Therefore we can use (3.9) to estimate the convergence factor. More precisely, to follow the double index notation (3.15), we write

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A} \le \min \limits _{P_k\in \pi ^1_k} \max _{\lambda _{\ell i}\in \sigma (A)} |P_k(\lambda _{\ell i})|\, . \end{aligned}$$

(3.16)

Now, for given $k\in \mathbb {N}$, let us write it as $k=k_1+k_2+\dots k_s$ and choose the polynomial

$$\begin{aligned} P^*_k(\lambda ):= \prod \limits _{m =1}^s \prod \limits _{j=1}^{k_m} \Bigl ( 1- \frac{\lambda }{\lambda _{mj}}\Bigr ) \end{aligned}$$

in (3.16). Then

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A} \le \max _{\lambda _{\ell i}\in \sigma (A)\}} |P^*_k(\lambda _{\ell i})|\, = \max _{\lambda _{\ell i}\in \sigma (A)\}} \prod \limits _{m =1}^s \prod \limits _{j=1}^{k_m } \Bigl | 1- \frac{\lambda _{\ell i}}{\lambda _{m j}}\Bigr | \, . \end{aligned}$$

Here the definition of $P^*_k(\lambda )$ implies that

$$\begin{aligned} P^*_k(\lambda _{\ell i})=0 \qquad \text{ for } \text{ all } \ \ell =1,\dots ,s, \ \ i=1,\dots , k_\ell \, , \end{aligned}$$

hence

$$\begin{aligned} \max _{\lambda _{\ell i}\in \sigma (A)\}} |P^*_k(\lambda _{\ell i})|\,= & {} \max _{\begin{array}{c} \ell =1,...,s\\ i\ge k_\ell +1 \end{array}} |P^*_k(\lambda _{\ell i})|\, \\= & {} \max _{\begin{array}{c} \ell =1,...,s\\ i\ge k_\ell +1 \end{array}} \prod \limits _{m =1}^s \prod \limits _{j=1}^{k_m } \Bigl | 1- \frac{\lambda _{\ell i}}{\lambda _{m j}}\Bigr |\, . \end{aligned}$$

Let us fix some $\lambda _{\ell i}$ and estimate the above product. As $m=1,...,s$, we only leave the terms for $m=\ell$ and estimate the other terms above by 1. Thus we obtain

$$\begin{aligned} \prod \limits _{m =1}^s \prod \limits _{j=1}^{k_m } \Bigl | 1- \frac{\lambda _{\ell i}}{\lambda _{m j}}\Bigr | \le \prod \limits _{j=1}^{k_\ell } \Bigl | 1- \frac{\lambda _{\ell i}}{\lambda _{\ell j}}\Bigr | = \prod \limits _{j=1}^{k_\ell } \frac{|\lambda _{\ell j}-\lambda _{\ell i}|}{|\lambda _{\ell j}|}\, . \end{aligned}$$

Here

$$\begin{aligned} \lambda _{\ell j}-\lambda _{\ell i}:= & {} \lambda _{\ell j}(A)-\lambda _{\ell i}(A)\\= & {} (\sigma _\ell + \mu _j (E_\ell ))- (\sigma _\ell + \mu _i (E_\ell ))\\= & {} \mu _j (E_\ell ) - \mu _i (E_\ell ) . \end{aligned}$$

Moreover, since $j\mapsto |\mu _j (E_\ell )|$ is a nonincreasing sequence and $j\le k_\ell < k_\ell +1\le i$, we have $|\mu _i (E_\ell ))|\le |\mu _j (E_\ell ))|$, hence, with the above relation,

$$\begin{aligned} |\lambda _{\ell j}-\lambda _{\ell i}| \le |\mu _j (E_\ell ) | + | \mu _i (E_\ell )| \le 2\, |\mu _j (E_\ell ) |. \end{aligned}$$

On the other hand, we have ${1\over \lambda _{\ell j}}\le \Vert A^{-1}\Vert$ since A is a positive operator with a complete eigensystem. Altogether,

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A}\le & {} \max _{\begin{array}{c} \ell =1,...,s \\ i\ge k_\ell +1 \end{array}} |P^*_k(\lambda _{\ell i})|\, \le \max _{\begin{array}{c} \ell =1,...,s \\ i\ge k_\ell +1 \end{array}} \prod \limits _{j=1}^{k_\ell } \frac{|\lambda _{\ell j}-\lambda _{\ell i}|}{|\lambda _{\ell j}|}\\\le & {} \max _{\ell =1,...,s} (2 \Vert A^{-1}\Vert )^{k_\ell } \prod \limits _{j=1}^{k_\ell } |\mu _j (E_\ell ) |\, . \end{aligned}$$

Using the arithmetic-geometric means inequality, we find that

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A} \le \max _{\ell =1,...,s} \Bigl ( 2 \Vert A^{-1}\Vert \, \frac{1}{k_\ell } \sum \limits _{j=1}^{k_\ell } |\mu _j (E_\ell ) | \Bigr )^{k_\ell }\, . \end{aligned}$$

(3.17)

Now we can use the above estimate for particular quasi-uniform decompositions, that is, for $k=k_1+k_2+\dots k_s$ in which all $k_\ell$ are chosen to satisfy

$$\begin{aligned} k_\ell \ge \lfloor \frac{k}{s} \rfloor \qquad (\ell =1,\dots ,s). \end{aligned}$$

(3.18)

Then all $k_\ell \rightarrow \infty$ as $k\rightarrow \infty$. Further, for all fixed $\ell$ we have $\mu _j (E_\ell )\rightarrow 0$ as $\ell \rightarrow \infty$, hence the arithmetic mean sequence $\frac{1}{k_\ell } \sum \limits _{j=1}^{k_\ell } |\mu _j (E_\ell ) |\rightarrow 0$ as well. Therefore, if k is large enough then the expression in the brackets in (3.17) is less than 1, and (3.18) implies

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A} \le \Bigl ( 2 \Vert A^{-1}\Vert \, \frac{1}{\lfloor \frac{k}{s} \rfloor } \sum \limits _{j=1}^{\lfloor \frac{k}{s} \rfloor } \max _{\ell =1,...,s} |\mu _j (E_\ell ) | \Bigr )^{\lfloor \frac{k}{s} \rfloor }\, . \end{aligned}$$

This readily implies (3.13).

A special situation occurs if there is only one nonzero operator among the compact perturbations. Then the above proof can be modified to reproduce the result in the same form as (3.12):

Theorem 3.2

Let the conditions of Theorem 3.1 hold, and in particular, assume that   $E_{| H_\ell }=0$ for $\ell \ge 2$. Then the error vectors of the CG algorithm for (3.5) satisfy

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A}\right) ^{1/k} \le \ \frac{2\Vert A^{-1}\Vert }{ k } \ \, \sum \limits _{j=1}^k \bigl | \mu _j(E_1) \bigr |\rightarrow 0 \qquad (\text{ as } \ k\rightarrow \infty ). \end{aligned}$$

(3.19)

Proof

We modify the proof of Theorem 3.1 from (3.17). Instead of a quasi-uniform decomposition $k=k_1+k_2+\dots k_s$, we simply choose $k_1=k$, and $k_\ell =0$ for $\ell \ge 2$. Since $\mu _j (E_\ell )=0$ for $\ell \ge 2$, we then have from (3.17) that

$$\begin{aligned} \frac{\Vert e_k\Vert _A}{\Vert e_0\Vert _A}\le & {} \max _{\ell =1,...,s} \Bigl ( 2 \Vert A^{-1}\Vert \, \frac{1}{k_\ell } \sum \limits _{j=1}^{k_\ell } |\mu _j (E_\ell ) | \Bigr )^{k_\ell }\, \\= & {} \Bigl ( 2 \Vert A^{-1}\Vert \, \frac{1}{k} \sum \limits _{j=1}^{k} |\mu _j (E_1 ) | \Bigr )^{k} \end{aligned}$$

which readily yields (3.19).

4 Block preconditioning and Krylov acceleration

In this section we consider block preconditioners and their effect on convergence in the context of Krylov iterations. It can be seen as a survey of earlier, with some new, results.

In Sect. 4.1 we address the need to use regularization. We discuss also the improvements of the Uzawa method, which is a basic defect-correction method, by use of a Krylov subspace iterative acceleration method. This is discussed in detail for Stokes type problems in Sect. 4.2 and 4.3. Our discussion is mostly on a general operator level, which also covers the situation when the operators are matrices arising from a finite element discretization.

4.1 Regularization of saddle-point problems

4.1.1 Motivation from optimization problems

As is familiar, constrained optimization problems arise in a multitude of applications. Such problems involve at least two variables, one of which is the Lagrange multiplier needed to impose the constraint. In the context of mixed variable or constrained finite element methods, the Lagrange multiplier acts as a natural physical variable such as the pressure in Stokes problem. The arising systems are normally symmetric and indefinite, but have a block matrix structure which can be utilized. Various types of preconditioners for such systems have been proposed through the years. For reduced matrix approaches, a Schur complement system for one of the variables must be solved.

The simplest optimization problem for a constraint equation $B\mathbf{{u}} = {g}$ takes the form

$$\begin{aligned} \inf _{p} \sup _\mathbf{{u}} \left\{ \frac{1}{2} \langle L \mathbf {u},\mathbf {u} \rangle - \langle \mathbf {u}, {f} \rangle + \langle B \mathbf {u} - {g}, {p} \rangle \right\} \end{aligned}$$

(4.1)

which leads to a linear system similar to (2.3), now allowing $g\ne 0$:

$$\begin{aligned} \begin{bmatrix} L &{} B^*\\ B &{} 0 \end{bmatrix} \begin{bmatrix} \mathbf {u} \\ {p} \end{bmatrix} = \begin{bmatrix} {f} \\ {g} \end{bmatrix} \end{aligned}$$

(4.2)

where B is surjective (in matrix case, it has full row rank) and L is symmetric. The block L can be indefinite in general, but we assume that L is positive definite on ker(B), which implies that for some sufficiently small $\varepsilon _0$, the operator $\varepsilon L + B^*B$ is positive definite for all $0< \varepsilon < \varepsilon _0$.

In this case the optimization problem (4.1) is augmented by the addition of a regularization term $\Vert B\mathbf {u} - {g}\Vert ^2/2$, which leads to the augmented system

$$\begin{aligned} \begin{bmatrix} L + \frac{1}{\varepsilon } B^*B &{} B^*\\ B &{} 0 \end{bmatrix} \begin{bmatrix} \mathbf {u} \\ {p} \end{bmatrix} = \begin{bmatrix} {f} + \frac{1}{\varepsilon }B^*{g} \\ {g} \end{bmatrix}. \end{aligned}$$

(4.3)

Since $B \mathbf {u} = {g}$, this is equivalent to (4.2) in the sense that both systems have the same solution. This method is particularly useful if L is indefinite or ill-conditioned. In particular, since $L +(1/\varepsilon )B^*B$ is positive definite, it follows readily that a solution exists. For such systems, the Schur complement ${S} = BL^{-1}B^*$ for (4.2) is replaced by ${S} = B(L+\frac{1}{\varepsilon }B^*B)^{-1}B^*$.

We also note that there exist weighted versions of such regularization, see, e.g., [5]. Based on the actual form of B and L one can estimate the value of $\varepsilon _0$, see e.g. [3].

We discuss first the LBB stability condition and then the solution of the regularized problem.

4.1.2 An algebraic form of the LBB condition

The optimization problems involve partial differential equations that for the actual solution must be discretized, which is normally done by use of a finite element method. To analyse the stability of discretized saddle point problems the LBB inf-sup condition is mostly used.

The LBB condition can be presented in algebraic form as follows. Assume then first that the LBB-condition holds for the $L_2$-norm. Here the discrete gradient matrix $B^*$ has a one-dimensional nullspace consisting of constant vectors, hence we consider the Schur complement for vectors in the orthogonal complement of this nullspace. In that subspace B has full rank.

Recall that the Moore-Penrose generalized inverse of B equals $B^{\dag }= B^*(BB^*)^{-1}$, in which case $BB^{\dag }={ I}$. The algebraic form of the LBB condition for the $L_2$-norm is

$$\begin{aligned} \gamma = \inf _{{p}}\sup _{{u}} \frac{\langle Bu,p\rangle }{\Vert {p}\Vert \Vert {u}\Vert }= \inf _{{p}}\frac{\Vert {p}\Vert }{\Vert B^{\dag }{p}\Vert } =\frac{1}{\Vert B^{\dag }\Vert }. \end{aligned}$$

Here, given p, the $\sup$ is taken for ${u} = B^{\dag }{p}$ (or its scalar multiple), for which $B{u} = {p}$.

In the matrix case, since $\Vert B^{\dag }\Vert = \sqrt{\varrho (B^{\dag ^*}B^{\dag })} = \sqrt{\varrho ((BB^*)^{-1})}= 1/\sqrt{\lambda _{\min }(BB^*)}$, we have

$$\begin{aligned} \gamma = \sqrt{\lambda _{\min }(BB^*)}. \end{aligned}$$

More generally, we obtain for the L-norm of u and an R-norm of the second saddle point variable p, where L and R are symmetric positive definite,

$$\begin{aligned} \gamma= & {} \inf _{{p}}\sup _{{u}} \frac{\langle Bu,p\rangle }{\sqrt{\langle Rp,p\rangle }\sqrt{\langle Lu,u\rangle }} = \inf _{{p}}\sup _{{u}} \frac{ \langle R^{-1/2} B L^{-1/2} (L^{1/2}{u}), (R^{1/2}{p}) \rangle }{\Vert R^{1/2}{p}\Vert \Vert L^{1/2}{u}\Vert }\\= & {} \inf _{{p}}\sup _{{z}} \frac{ \langle R^{-1/2} B L^{-1/2} {z}, s \rangle }{\Vert {s}\Vert \Vert {z}\Vert } = \sqrt{\lambda _{\min } (R^{-1/2}BL^{-1}B^*R^{-1/2})}. \end{aligned}$$

For the Stokes problem we have $R=I_2$ and L equals the block Laplacian,that is, the L-norm equals the first-order Sobolev norm for the corresponding function space.

As seen from the above, $\gamma >0$ (owing to considering the orthogonal complement of the one-dimensional nullspace of $B^*$); however, $\gamma$ can be small. Then one must regularize the problem, writing it in the form

$$\begin{aligned} \begin{bmatrix} L &{} B^*\\ B &{} -C \end{bmatrix} \begin{bmatrix} \mathbf {u} \\ p \end{bmatrix} = \begin{bmatrix} {f} \\ {g} - C {p} \end{bmatrix}. \end{aligned}$$

Here C is symmetric and positive semidefinite, and it is positive definite on the null space $ker(B^*)$ of $B^*$. For Stokes problem one can let it be diagonal. For the corresponding Schur complement the lower spectral bound is positive: in the matrix case,

$$\begin{aligned} \gamma = \lambda _{\min } (C+BL^{-1}B^*) >0 . \end{aligned}$$

For the LBB-condition to hold in finite element problems one must use stable element pairs for the two variables, which implies that for the Stokes problem, the space V for velocity must be sufficiently richer than the space W for pressure.

On the other hand, when finite element methods are implemented on parallel computer platforms, the data communication is simplified if one uses equal order finite elements for V and W. To stabilize for this, or to increase the stabilization even when one uses some stable element pairs, but where the constant $\gamma$ is too small (such as for the mini-element, see [4]), one must use a stabilization term, $-\alpha C$, for some scalar $\alpha$, depending on the actual form of B and L, see e.g. [3]. As has been shown in [4] for Stokes problem $\alpha = O(h)$, where h is the discretization parameter.

We note that the addition of the stabilization term can be done without any ’over-stabilization’ effects, such as loss of order of the approximate solution, as the right-hand side is correspondingly modified, see [4] for further details.

4.1.3 The Uzawa method in the context of regularization

We now return to the first regularized form (4.3), and show its relation with the Uzawa method. First we need the following technical result:

Lemma 4.1

Let $L_{\varepsilon } = \varepsilon L + B^*B$, where L is positive definite. Then

• (a) $BL_{\varepsilon }^{-1} = (\varepsilon I + BL^{-1}B^*)^{-1} BL^{-1}$,

• (b) $BL_{\varepsilon }^{-1} B^*= I - \varepsilon (\varepsilon I + BL^{-1}B^*)^{-1}$

and the nonzero eigenvalues of $BL_{\varepsilon }^{-1}B^*$ are contained in the interval $[\lambda _1/(\varepsilon + \lambda _1), 1)$, where $\lambda _1$ is the smallest nonzero eigenvalue of $BL^{-1}B^*$.

Proof

Use a direct computation or Sherman–Morrison–Woodbury formula. $\square$

The Uzawa method can be presented in the following way. Let

$$\begin{aligned} \ell _{\varepsilon }(\mathbf{u}, {p}) = \frac{1}{2} \langle L\mathbf{u},\mathbf{u}\rangle - \langle \mathbf{u}, {f} \rangle + \langle B\mathbf{u} - {g}, {p} \rangle + \frac{1}{2 \varepsilon } \Vert B\mathbf{u} - {g}\Vert ^2 \end{aligned}$$

be the Lagrangian functional corresponding to the regularized constrained optimization problem for a given $\varepsilon > 0$. The solution $\hat{\mathbf{u}} \in V = \mathbb {R}^n$, $\hat{{p}} \in X = \mathbb {R}^m$ is a saddle point of $\ell _{\varepsilon }(\mathbf{u}, {p})$ and, given p, we have

$$\begin{aligned} \varphi ({p}) \equiv \ell _{\varepsilon } (\widehat{\mathbf{u}}({p}), {p}) = \min _{\mathbf{u} \in V} \ell _{\varepsilon }(\mathbf{u}, {p}) \end{aligned}$$

(4.4)

For this functional the first order derivative satisfies $\nabla \varphi ({p}) = B\hat{\mathbf{u}}({p}) -{g}$ and the Hessian is $\nabla ^2 \varphi ({p}) = -B(L + \frac{1}{\varepsilon } B^*B)^{-1}B^*= - \varepsilon BL_{\varepsilon }^{-1}B^*$. Since the Hessian matrix is negative definite on the range of B, hence $\varphi ({p})$ has a minimum at $\widehat{{p}}$ and when $\varepsilon \ll 1$, it follows from Lemma 4.1 that $\nabla ^2 \varphi ({p}) \approx -\varepsilon I$. Using the approximation

$$\begin{aligned} - \nabla ^2 \varphi ({p}_0)({p} - {p}_0) \approx \nabla \varphi ({p_0}). \end{aligned}$$

and the above-mentioned relation $\nabla ^2 \varphi ({p}) \approx -\varepsilon I$ for the initial guesses, the method takes the simple form

$$\begin{aligned} {p}_1 - {p}_0 = \frac{1}{\varepsilon } (B\mathbf{u}_0 - {g}). \end{aligned}$$

Consequently, a regularized form of the Uzawa algorithm takes the form

$$\begin{aligned} \begin{array}{ccl} &{}&{}{p} := {p}_0\\ &{}{R}:&{}\mathbf {u} := \text {minimizer of}\ \ell _{\varepsilon }(\mathbf{u}, \mathrm{p})\\ &{}&{}{c} := B \mathbf{u} - {g}\\ &{}&{}{p} :={p} + \tau {c}\\ &{}&{}\text {If}\ \Vert {c}\Vert ^2 > { \tilde{\varepsilon }},\ \text {goto}\ R \end{array} \end{aligned}$$

where $\tilde{\varepsilon } \ll 1$ and $\tau = 1/\varepsilon$ is an appropriate choice.

It is readily seen that this method is equivalent to a stabilized block Gauss–Seidel iteration method, namely, given ${p}_0$, for $k = 0, 1, \ldots$, until convergence, let

$$\begin{aligned} \begin{bmatrix} L + \frac{1}{\varepsilon } B^*B &{} 0 \\ B &{} -\varepsilon I \end{bmatrix} \begin{bmatrix} \mathbf {u}_{k+1} \\ {p}_{k+1} \end{bmatrix} = - \begin{bmatrix} 0 &{} B^*\\ 0 &{} \varepsilon I \end{bmatrix} \begin{bmatrix} \mathbf {u}_{k} \\ {p}_{k} \end{bmatrix} + \begin{bmatrix} {f+\frac{1}{\varepsilon } B^*g} \\ {g} \end{bmatrix}. \end{aligned}$$

In practice, solutions of systems with the matrix $L + (1/\varepsilon )B^*B$ can be costly. Therefore, we consider next a generalized block Gauss-Seidel matrix, used as a preconditioner in an iterative solution method, where the arising linear systems are easier to solve.

4.2 Block Gauss-Seidel preconditioner for a basic Krylov acceleration method

We consider now preconditioners for the unreduced system (4.2). The considered 2 by 2 block matrices may contain operator blocks in general. Let $D_1$, $D_2$ be symmetric positive definite preconditioners to L and $BD_1^{-1}B^*$, respectively. Convergent choices are discussed at the end of this subsection. Then

$$\begin{aligned} \begin{bmatrix} D_1 &{} 0 \\ B &{} -D_2 \end{bmatrix} \end{aligned}$$

(4.5)

can be used as a simple, but still efficient preconditioner on block triangular form to $\left[ \begin{array}{ll}L &{} B^{*} \\ B &{} 0 \end{array}\right]$. The operator matrix (4.5) corresponds to the matrix splitting

$$\begin{aligned} \begin{bmatrix} D_1 &{} 0 \\ B &{} -D_2 \end{bmatrix} = \begin{bmatrix} L &{} B^*\\ B &{} 0 \end{bmatrix} - \begin{bmatrix} L-D_1 &{} B^*\\ 0 &{} D_2 \end{bmatrix}. \end{aligned}$$

For the analysis of this preconditioner we must analyse the eigenvalues ($\lambda$) of

$$\begin{aligned} \begin{bmatrix} D_1 &{} 0 \\ B &{} -D_2 \end{bmatrix}^{-1} \begin{bmatrix} L &{} B^*\\ B &{} 0 \end{bmatrix} = \begin{bmatrix} D_1^{-1} &{} 0 \\ D_2^{-1}BD_1^{-1} &{} D_2^{-1} \end{bmatrix} \begin{bmatrix} L &{} B^*\\ B &{} 0 \end{bmatrix}, \end{aligned}$$

(4.6)

which equal $\lambda = 1 + \delta$, where $\delta$ denotes the eigenvalues of the preconditioned residual matrix, i.e.

$$\begin{aligned} \begin{bmatrix} D_1 &{} 0 \\ B &{} -D_2 \end{bmatrix}^{-1} \begin{bmatrix} L-D_1 &{} B^*\\ 0 &{} D_2 \end{bmatrix} = \begin{bmatrix} D_1^{-1}(L-D_1) &{} D_1^{-1}B^*\\ D_2^{-1}BD_1^{-1}(L-D_1) &{} D_2^{-1}BD_1^{-1}B^*-I_2 \end{bmatrix}. \end{aligned}$$

Using a similarity transformation with the matrix $\begin{bmatrix}D_1^{1/2} &{} 0 \\ 0 &{} D_2^{1/2} \end{bmatrix}$ and letting $\widetilde{L} = D_1^{-1/2} LD_1^{-1/2}$, $\widetilde{B} = D_2^{-1/2}BD_1^{-1/2}$, $\widetilde{\mathbf{u}} = D_1^{1/2} \mathbf {u}$ and $\widetilde{{p}} = D_2^{1/2}{p}$ we find

$$\begin{aligned} \delta \begin{bmatrix} \widetilde{\mathbf{u}} \\ \widetilde{{p}} \end{bmatrix} = \begin{bmatrix} \widetilde{L} - I_1 &{} \widetilde{B}^*\\ \widetilde{B}(\widetilde{L}-I_1) &{} \widetilde{B}\widetilde{B}^*- I_2 \end{bmatrix} \begin{bmatrix} \widetilde{\mathbf{u}} \\ \widetilde{{p}} \end{bmatrix}. \end{aligned}$$

(4.7)

A computation shows that

$$\begin{aligned} \begin{array}{rcl} (1 + \delta ) \widetilde{{p}} &{}=&{} \delta \widetilde{B} \widetilde{\mathbf{u}} \\ (1+\delta )(\widetilde{L} - I_1)\widetilde{\mathbf{u}} + \delta \widetilde{B}^*\widetilde{B} \widetilde{\mathbf{u}} &{}=&{} \delta (1 + \delta ) \widetilde{\mathbf{u}} \end{array} \end{aligned}$$

(4.8)

If $\widetilde{\mathbf{u}} = 0$ then it follows that $\widetilde{{p}} = 0$. Therefore, $\widetilde{\mathbf{u}} \not = 0$ for any eigenvector of (4.7) and a multiplication of the second equation in (4.8) yields

$$\begin{aligned} \delta ^2 \Vert \widetilde{\mathbf{u}}\Vert ^2 - [\widetilde{\mathbf{u}}^* (\widetilde{L} - I_1) \widetilde{\mathbf{u}} + (\Vert \widetilde{B}\widetilde{\mathbf{u}}\Vert ^2 - \Vert \widetilde{\mathbf{u}}\Vert ^2)] \delta - \widetilde{\mathbf{u}}^* (\widetilde{L} - I_1)\widetilde{\mathbf{u}} = 0. \end{aligned}$$

Denote $a = \widetilde{\mathbf{u}}^*(\widetilde{L} - I_1)\widetilde{\mathbf{u}}/\Vert \widetilde{\mathbf{u}}\Vert ^2$ and $b = \Vert \widetilde{B}\widetilde{\mathbf{u}}\Vert /\Vert \widetilde{\mathbf{u}}\Vert$. Then $\delta ^2 - (a+b^2 -1)\delta -a =0$ and

$$\begin{aligned} \delta = \frac{1}{2}(a+b^2-1) \pm \frac{1}{2}\sqrt{(a+b^2-1)^2 +4a}. \end{aligned}$$

This result is collected in the next theorem.

Theorem 4.1

Let $\mathcal {D} = \begin{bmatrix} D_1 &{} 0 \\ B &{} -D_2 \end{bmatrix}$ be a preconditioner to $\mathcal {A} = \begin{bmatrix} L &{} B^*\\ B &{} 0 \end{bmatrix}$ and let $\widetilde{L} = D_1^{-1/2}LD_1^{-1/2}$, $\widetilde{B} = D_2^{-1/2}BD_1^{-1/2}$. Then the eigenvalues of $\mathcal {D}^{-1}\mathcal {A}$ satisfy $\lambda = 1+ \frac{1}{2}(a+b^2-1)\pm \sqrt{(a+b^2-1)^2+4a}$, where $a=\widetilde{\mathbf{u}}^*(\widetilde{L}-I_1)\widetilde{\mathbf{u}}/\Vert \widetilde{\mathbf{u}}\Vert ^2$, $b=\Vert \widetilde{B}\widetilde{\mathbf{u}}\Vert /\Vert \widetilde{\mathbf{u}}\Vert$, $\widetilde{\mathbf{u}} = D_1^{1/2}\mathbf {u}$ and $[\mathbf {u}, {p}]$ is an eigenvector of $\mathcal {D}^{-1}\mathcal {A}$.

It follows that if $D_1 =L$ then $a=0$ and $\delta = \left\{ \begin{array}{l} b^2 - 1 \\ 0 \end{array} \right.$. Hence the eigenvalues of (4.6) are real and equal the unit number (in the matrix case with multiplicity at least n) respectively to the eigenvalues of $\widetilde{B}\widetilde{B}^*$, i.e. of $D^{-1}_2 BD_1^{-1} B^*$, which latter are positive. By choosing $D_2$ sufficiently close to $BD_1^{-1}B^*$ we can hence cluster the eigenvalues around the unit number. If $D_1$ is diagonal, then we can form the matrix $BD_1^{-1}B^*$ explicitly. This holds also if |a| is small. However, if b is small (which occurs for a nearly rank-deficient matrix B) then $\delta$ can take values close to a and $-1$, which means that the preconditioned matrix is nearly singular. Further, it can be seen that if $-(b + 1)^2< a < - (b - 1)^2$, then the eigenvalues are complex.

It can hence be concluded that the above preconditioning method does not have a fully robust behaviour.

Even $D_1$ or $D_2$ is itself a differential operator, its discretization can be solved by inner iterations to some limited accuracy. As shown e.g. [4, 8], conjugate gradient Krylov subspace methods are quite insensitive to the inner iteration tolerance. As shown e.g. in [30], the pure Uzawa method is more sensitive.

Depending on the expense in solving systems with $D_1$ and $D_2$, this method can work quite efficiently. However, due to the strong unsymmetry of the iteration matrix, the norm of the corresponding matrix in (4.7) can be large and this must be compensated for by more iterations. Therefore we turn now to a symmterizable form of preconditioned matrix.

4.3 A symmetrized form of a block Gauss-Seidel preconditioner

In [8], a one-sided symmetrization of a block Gauss-Seidel preconditioned matrix was proposed. Therein, the method was formulated as a block Gauss-Seidel method, which was subsequently symmetrized by choosing a proper implicit inner product (cf. [5, 14, 15, 26] for a similar approach). We show below that the method can be formulated algebraically, using a modification of the Gauss-Seidel matrix. Let then $L_0$ be a symmetric positive definite preconditioner to L which has been scaled to satisfy $\langle L_0 \mathbf {u}, \mathbf {u}\rangle \le \alpha _1 \langle L \mathbf {u}, \mathbf {u}\rangle$ for all $\mathbf {u}\in \mathbb {R}^n$, where $0<\alpha _1<1$. After applying a block Gauss-Seidel preconditioner in (inverse) multiplicative form, the preconditioned matrix becomes

$$\begin{aligned} \begin{bmatrix} L_0^{-1} &{} 0 \\ BL_0^{-1} &{} -I_2 \end{bmatrix} \begin{bmatrix} L &{} B^*\\ B &{} -C \end{bmatrix} = \begin{bmatrix} L_0 L^{-1} &{} L_0^{-1}B^*\\ B(L_0^{-1}L - I_1) &{} C+BL_0^{-1}B^*\end{bmatrix} \end{aligned}$$

(where C is symmetric positive semidefinite, possibly zero). After multiplication with $\begin{bmatrix} L-L_0 &{} 0 \\ 0 &{} I_2 \end{bmatrix}$ it becomes

$$\begin{aligned} \begin{bmatrix} (L-L_0)L_0^{-1} &{} 0 \\ BL_0^{-1} &{} -I_2 \end{bmatrix} \begin{bmatrix} L &{} B^*\\ B &{} -C \end{bmatrix} = \begin{bmatrix} L(L_0^{-1}-L^{-1})L &{} (LL_0^{-1}-I_1)B^*\\ B(L_0^{-1}L - I_1) &{} C+BL_0^{-1}B^*\end{bmatrix}. \end{aligned}$$

This matrix is not only symmetric but also positive definite. The latter is readily seen if we first rewrite it in the form

$$\begin{aligned} \begin{bmatrix} L_0^{1/2}(\widetilde{L}^{2}-\widetilde{L})L_0^{1/2} &{}\quad L_0^{1/2}(\widetilde{L}-I_1) \widetilde{B}^*\\ \widetilde{B}(\widetilde{L} - I_1)L_0^{1/2} &{}\quad C+\widetilde{B} \widetilde{B}^*\end{bmatrix} \end{aligned}$$

where $\widetilde{L}=L_0^{-1/2}LL_0^{-1/2}$, hence $\widetilde{L} - I_1$ is positive definite, and $\widetilde{B}=BL_0^{-1/2}$, whose Schur complement is seen to be $C+\widetilde{B}\widetilde{L}^{-1}\widetilde{B}^*$, which by assumption is positive definite.

The advantages with the above method are that, contrary to the standard Gauss-Seidel preconditioner, one can use a classical preconditioned conjugate gradient method for symmetric positive definite problems and that, contrary to the Schur complement method, no inner iterations are required (they have been replaced by one action of $L_0^{-1}$ and one of L per iteration step). The disadvantages are that the rate of convergence depends on the condition number of both matrices $L_0^{-1/2}LL_0^{-1/2}-I_1$ and $C+BL^{-1}B^*$. It requires therefore a particularly accurate preconditioner $L_0$ and is less robust when B is nearly rank-deficient. Ill-conditioning of the second matrix can to some extent be handled by a proper choice of a regularization matrix C, see [3] for further details.

5 Superlinear convergence of the Krylov-Uzawa iteration for the Stokes problem

As mentioned earlier, Krylov subspace methods typically lead to a steadily reduced spectral condition number, which, under proper circumstances, may result in a superlinear increase of the rate of convergence. In this section we show that the Krylov-Uzawa iteration (3.4) may indeed exhibit superlinear convergence on the operator level. To our knowledge, no superlinear result has been proved before in the context of the Stokes problem.

The result relies on a technical background that exploits a smoothness assumption on the boundary. Namely, following Theorem 2.1, we assume that $\Omega$ is connected and its boundary is in class $C^3$. The mentioned background shows that one in fact cannot expect superlinear convergence for non-smooth domains, see Remark 5.1 below.

The starting point to the required estimates is Theorem 3.1, which we have proved in subsect. 3.2.2. In order to apply this result, we first have to derive a quantitative measure of the compactness of the operator K that appears in Theorem 2.1. In fact, the sums of eigenvalues behave as the sums for sequences $O(j^{-{2\over d}})$ (where d is the dimension).

Theorem 5.1

If $\partial \Omega \in C^3$, then the ordered eigenvalues $\mu _j(K)$ of the compact operator K in Theorem 2.1 satisfy

$$\begin{aligned} \sum \limits _{i=1}^j |\mu _i(K)|\le \left\{ \begin{array}{ll} O(\ln j) &{} \ \text{ if }\ d=2 \\ O(j^{1/3}) &{} \ \text{ if }\ d=3 \end{array} \right. \qquad (\forall j\in \mathbf{N}^+). \end{aligned}$$

Proof

Consider the following real Hilbert spaces:

$$\begin{aligned} \begin{array}{l} {\dot{H}}^1(\Omega ):= \{ p\in H^1(\Omega ): \ {\int \limits _\Omega p=0} \}, \\ {\dot{H}}^1_M(\Omega ):= \, \text{ the } \text{ closure } \text{ of } \ {\dot{H}}^1(\Omega )\cap M \ \text{ in } \ {\dot{H}}^1(\Omega ), \end{array} \end{aligned}$$

both with the inner product and corresponding norm

$$\begin{aligned} \langle p,q\rangle _{{H}^1}:= \int _{\Omega } \nabla p\cdot \nabla q, \qquad \Vert p\Vert _{{H}^1}^2 = \int _{\Omega } |\nabla p|^2\, . \end{aligned}$$

Theorem 2.1 yields that there exists a constant $C>0$ such that for all $p\in M$ we have $Kp\in {\dot{H}}^1_M(\Omega )$ and

$$\begin{aligned} \Vert Kp\Vert _{{H}^1}\le C\Vert p\Vert _{L^2} \qquad (\forall p\in M). \end{aligned}$$

(5.1)

Here K is self-adjoint in M since S is self-adjoint. Since K is also compact, it has countably many eigenvalues satisfying $\mu _j\rightarrow 0$ as $j\rightarrow \infty$. Consider the nonzero eigenvalues. For a given eigenfunction $p_j$, the facts $Kp_j\in {\dot{H}}^1_M(\Omega )$ and $Kp_j = \mu _jp_j$ imply that $p_j\in {\dot{H}}^1_M(\Omega )$ itself.

Let $K_{H^1}$ denote the restriction $K_{|{\dot{H}}^1_M(\Omega )}$ considered as an operator in the space ${\dot{H}}^1_M(\Omega )$. The above imply that K has the same nonzero eigenvalues as $K_{H^1}$, briefly,

$$\begin{aligned} \mu _j(K) = \mu _j(K_{H^1}) \qquad \text{ for } \ j\in \mathbb {N}^+ \end{aligned}$$

whenever $\mu _j(K)>0$. Here $K_{H^1}$ is no more necessarily self-adjoint in the ${H}^1$-inner product, hence it is better characterized by its singular values

$$\begin{aligned} s_j(K_{H^1}):= \min \limits _{H_{j-1}\subset {\dot{H}}^1_M(\Omega )} \, \max \limits _{p \bot H_{j-1} } \frac{\Vert Kp\Vert _{{H}^1}}{\Vert p\Vert _{{H}^1}} \, , \end{aligned}$$

where $H_{i-1}$ stands for an arbitrary $(i-1)$-dimensional subspace, see [22, Chap. VI.]. The singular values do not decrease if one considers a larger space (see [22, Prop. VI.1.4]), hence ${\dot{H}}^1_M(\Omega )$ can be replaced by $H^1(\Omega )$ and (5.1) can also be used to obtain

$$\begin{aligned} s_j(K_{H^1}) \le \ C \! \min \limits _{H_{j-1}\subset H^1(\Omega )} \, \max \limits _{p \bot H_{j-1} } \frac{\Vert p\Vert _{L^2} }{\Vert p\Vert _{{H}^1}} \ . \end{aligned}$$

The latter mimimax values are the approximation numbers of the Sobolev embedding of $H^1(\Omega )$ into $L^2(\Omega )$, which are inversely related to those of the Neumann Laplacian eigenvalues on $\Omega$, known to be $O(j^{2/d})$ (where d is the dimension), due to the classical result of Weyl [11]. This yields

$$\begin{aligned} s_j(K_{H^1}) \le O(j^{-2/d})\qquad (\forall j\in \mathbf{N}^+). \end{aligned}$$

Further, [22, Cor. 2.4] implies that

$$\begin{aligned} \sum \limits _{i=1}^j |\mu _i(K_{H^1})|\le \sum \limits _{i=1}^j s_i(K_{H^1}) , \end{aligned}$$

hence with the above, for all $j\in \mathbf{N}^+$,

$$\begin{aligned} \sum \limits _{i=1}^j |\mu _i(K)| = \sum \limits _{i=1}^j |\mu _i(K_{H^1}) |\le \sum \limits _{i=1}^j s_i(K_{H^1}) \le const.\cdot \sum \limits _{i=1}^j i^{-2/d}\le \left\{ \begin{array}{ll} O(\ln j) &{} \ \text{ if }\ d=2 \\ O(j^{1/3}) &{} \ \text{ if }\ d=3 \end{array} \right. \end{aligned}$$

where the latter follows with elementary analysis by comparing with $\int _1^j x^{-2/d} \text{ d }x$, see also [7, Prop. 4.4]. Thus we have obtained the desired estimate.

Remark 5.1

 (i) The asymptotics in Theorem 5.1 is not sharp for all cases: under some symmetry property of the domain, $|\mu _j(K)|$ themselves may decrease faster than $O(j^{-{2\over d}})$. For instance, on a ball in 3D one has $\mu _j(K) = -\frac{1}{2(2j+1)}$, and on a disk in 2D the operator K is simply the zero operator [18, 32].  (ii) The smoothness of the boundary is important in Theorem 2.1 and hence also in Theorem 5.1. For instance, a polygonal corner even contributes an interval to the essential spectrum of the Cosserat operator [17], which implies that one cannot obtain superlinear convergence estimates in that case.

Based on the previous results, we can now derive the our main theorem on the superlinear convergence for the Stokes problem.

Theorem 5.2

Let $\partial \Omega \in C^3$. Let us apply the Krylov–Uzawa iteration (3.4) for the Stokes problem (1.1) in the space $L^2_0(\Omega )$. Then

$$\begin{aligned} \left( \Vert \mathbf{u}_{k+1} - \mathbf{u}^*\Vert _{H^1_0} + \Vert p_k-p^*\Vert _{L^2}\right) ^{1/k} \le \left\{ \begin{array}{ll} O(\frac{\ln k}{k}) &{} \ (\text{ if }\ d=2) \\ O(k^{-2/3}) &{} \ (\text{ if }\ d=3) \end{array} \right. \quad \rightarrow 0 \quad (\text{ as } \ k\rightarrow \infty ). \end{aligned}$$

(5.2)

Proof

Let us consider the space $H=L^2_0(\Omega )$ and the operator $A:=S$ (the Schur complement operator), where $s=2$, with the subspaces and operators

$$\begin{aligned} H_1:=M, \quad H_2:=N, \qquad E_1:=K, \quad E_2:=0, \end{aligned}$$

respectively. The conditions of Theorem 3.1 are satisfied: indeed, (3.14) holds, since Theorem 2.1 implies that $S_{|M}=\frac{1}{2}I+K$ for some compact operator $K:M\rightarrow M$, and $S_{|N}= I = 1\cdot I+0$, where $H=L^2_0(\Omega )=M\oplus N$.

In fact, in operator matrix form we have

$$\begin{aligned} S= \begin{bmatrix} \frac{1}{2}I+K &{} 0 \\ 0 &{} I \end{bmatrix}\, . \end{aligned}$$

Due to $E_2:=0$, we can also apply Theorem 3.2. Then (3.19) yields

$$\begin{aligned} \left( \frac{\Vert e_k\Vert _S}{\Vert e_0\Vert _S}\right) ^{1/k} \le \ \frac{2\Vert S^{-1}\Vert }{ k } \ \, \sum \limits _{j=1}^k \bigl | \mu _j(K) \bigr | \end{aligned}$$

(5.3)

for the error vectors

$$\begin{aligned} e_k:=p_k-p^* . \end{aligned}$$

Now (2.6) implies that $\Vert S^{-1}\Vert \le \gamma ^{-2}$ and that $\gamma \Vert e\Vert _{L^2}\le \Vert e\Vert _S \le \Vert e\Vert _{L^2}$ (for all $e\in L^2_0(\Omega )$). Using (5.3) and Theorem 5.1, we thus obtain

$$\begin{aligned} const.\cdot \Vert p_k-p^*\Vert _{L^2}^{1/k} \le \left( \frac{\Vert e_k\Vert _{L^2} }{\Vert e_0\Vert _{L^2} }\right) ^{1/k} \le \left\{ \begin{array}{ll} O(\frac{\ln k}{k}) &{} \ \text{ if }\ d=2 \, ; \\ O(k^{-2/3}) &{} \ \text{ if }\ d=3\, . \end{array} \right. \end{aligned}$$

(5.4)

Finally we show that $\Vert \mathbf{u}_{k+1} - \mathbf{u}^*\Vert _{H^1_0}$ inherits the estimate for $\Vert p_k-p^*\Vert _{L^2}$. Due to the definition of the auxiliary variable $\mathbf{u}_{k+1}:= \Delta ^{-1}(\nabla p_k-\mathbf{f})$, we have

$$\begin{aligned} -\Delta \mathbf{u}_{k+1} + \nabla p_k = \mathbf{f}, \qquad \mathbf{u}_{k+1\, \mid \partial \Omega } = 0 \end{aligned}$$

just as in the Uzawa iteration. Problem (1.1) itself includes a similar relation:

$$\begin{aligned} -\Delta \mathbf{u}^* + \nabla p^* = \mathbf{f}, \qquad \mathbf{u}^*_{\ \mid \partial \Omega } = 0 , \end{aligned}$$

hence

$$\begin{aligned} -\Delta (\mathbf{u}_{k+1} - \mathbf{u}^*) = \nabla (p^* -p_k). \end{aligned}$$

Multiplying with $\mathbf{u}_{k+1} - \mathbf{u}^*$ and integrating,

$$\begin{aligned} \Vert \mathbf{u}_{k+1} - \mathbf{u}^*\Vert _{H^1_0}^2= & {} - \int _{\Omega } \Delta (\mathbf{u}_{k+1} - \mathbf{u}^*) \cdot (\mathbf{u}_{k+1} - \mathbf{u}^*) = \int _{\Omega } \nabla (p^* -p_k) \cdot (\mathbf{u}_{k+1} - \mathbf{u}^*) \\= & {} - \int _{\Omega } (p^* -p_k) \cdot \mathrm{div}\,(\mathbf{u}_{k+1} - \mathbf{u}^*) \le \Vert p_k-p^*\Vert _{L^2} \Vert \mathrm{div}\,(\mathbf{u}_{k+1} - \mathbf{u}^*)\Vert _{L^2}\\\le & {} \Vert p_k-p^*\Vert _{L^2} \Vert \mathbf{u}_{k+1} - \mathbf{u}^*\Vert _{H^1_0}, \end{aligned}$$

hence

$$\begin{aligned} \Vert \mathbf{u}_{k+1} - \mathbf{u}^*\Vert _{H^1_0} \le \Vert p_k-p^*\Vert _{L^2} \, . \end{aligned}$$

Altogether, the theorem is thus proved.