Abstract
Learning from successful applications of methods originating in statistical mechanics, complex systems science, or information theory in one scientific field (e.g., atmospheric physics or climatology) can provide important insights or conceptual ideas for other areas (e.g., space sciences) or even stimulate new research questions and approaches. For instance, quantification and attribution of dynamical complexity in output time series of nonlinear dynamical systems is a key challenge across scientific disciplines. Especially in the field of space physics, an early and accurate detection of characteristic dissimilarity between normal and abnormal states (e.g., pre-storm activity vs. magnetic storms) has the potential to vastly improve space weather diagnosis and, consequently, the mitigation of space weather hazards.
This review provides a systematic overview on existing nonlinear dynamical systems-based methodologies along with key results of their previous applications in a space physics context, which particularly illustrates how complementary modern complex systems approaches have recently shaped our understanding of nonlinear magnetospheric variability. The rising number of corresponding studies demonstrates that the multiplicity of nonlinear time series analysis methods developed during the last decades offers great potentials for uncovering relevant yet complex processes interlinking different geospace subsystems, variables and spatiotemporal scales.
Similar content being viewed by others
1 Introduction
Solar coronal mass ejections (CMEs) colliding at high speeds of up to 3000 km/s with the Earth’s magnetosphere can cause extremely intense magnetic storms and sudden magnetic field changes (and electric field pulses) both in the magnetosphere and at the Earth’s surface. Tsurutani and Lakhina (2014) found that a “perfect” interplanetary CME (ICME) could create a magnetic storm with intensity up to the saturation limit, with the disturbance storm-time index \((\mathrm{Dst}) \sim -2500\text{ nT}\), a value greater than the one estimated for the famous Carrington storm. The interplanetary shock would arrive at Earth within ∼12 h with a magnetosonic Mach number ∼45, comparable to astrophysical shocks. Moreover, the associated magnetospheric electric field would form a new relativistic electron radiation belt. Eventually, the dayside and nightside shock-related auroral events might cause geomagnetically induced currents (GICs) at the surface of the Earth, which in turn could lead to the collapse of power systems over large geographical areas. Recently, Welling et al. (2021) used the estimates provided by Tsurutani and Lakhina (2014) to drive a coupled magnetohydrodynamic-ring current-ionosphere model of geospace to obtain more physically accurate estimates of the geospace response to such an event. The new result regarding GIC levels exceeds values observed during historic extreme events, including the March 1989 event that brought down the Hydro-Québec power grid in eastern Canada. Such an extreme space weather scenario illustrates, on the one hand, the need for reliable operational space weather prediction schemes but also, on the other hand, the necessity to understand the underlying physical mechanisms that correspond to an open spatially extended nonequilibrium (input-output) dynamical system, as is the Earth’s magnetosphere (Consolini et al. 2008; Balasis et al. 2009).
The solar wind-magnetosphere system has been shown to be nonlinear (e.g., Tsurutani et al. 1990; Johnson and Wing 2005; Reeves et al. 2011; Wing et al. 2016 and references therein). Indeed, since the early 1990s it was shown how the dynamics of the Earth’s magnetosphere-ionosphere system in response to the changes of the interplanetary medium and to the solar wind displays a nonlinear, chaotic and near-criticality (avalanche) dynamics especially during magnetospheric substorms (e.g., Chang 1992, 1998, 1999; Klimas et al. 1996; Consolini et al. 1996; Consolini 1997; Uritsky and Pudovkin 1998; Lui et al. 2000; Uritsky et al. 2002). In particular, in Consolini et al. (1996) evidenced that the character of the magnetospheric dynamics as monitored by the auroral electrojet (AE) index cannot be simply assumed to be low-dimensional, showing, indeed, multifractal features similar to intermittent turbulence. Later, analyses on the busty-dynamics and on the self-similarity features of geomagnetic indices and auroral images (Consolini 1997; Uritsky and Pudovkin 1998; Chapman et al. 1998; Lui et al. 2000; Klimas et al. 2000; Uritsky et al. 2002) suggested that the magnetospheric dynamics display features similar to those of a non-equilibrium system near a critical point of the dynamics (see also, Chang 1999; Consolini 2002). In this framework, the magnetospheric substorms, which are among the main manifestations of the solar wind-magnetosphere-ionosphere coupling, were associated with the occurrence of non-equilibrium dynamical phase transitions, mainly involving the plasma confined in the central plasma sheet (CPS) region of the near-Earth magnetotail (Sitnov et al. 2000, 2001; Sharma et al. 2001) – a region which is characterized by turbulence and a complex dynamics (Borovsky et al. 1997; Borovsky and Funsten 2003). Nowadays, the dynamics of the Earth’s magnetosphere is regarded as an open spatially extended non-equilibrium system displaying dynamical complexity and self-organization (Klimas et al. 2000; Consolini et al. 2008; Borovsky and Valdivia 2018). The term dynamical complexity refers to a specific quantifiable physical property and has not to be read as a jargon to refer to fascinating complicated phenomena. According to Chang et al. (2006) dynamical complexity is a phenomenon deeply rooted in the nature that emerges in nonlinear interacting systems, when a multitude of structures/subsystems at different spatio-temporal scales are formed and interact generating a pseudo-stochastic dynamics. Furthermore, a peculiar feature of dynamical complexity is that the evolution laws of the global system cannot be directly surmised from the elemental laws that regulate the dynamics of the single parts. In this framework, the Earth’s magnetosphere-ionosphere system, which consists of several nonlinearly interacting plasma regions and, inside of each of these regions, of different physical structures at different spatio-temporal scales, can display dynamical complexity in response to solar wind and interplanetary medium changes.
Dynamical complexity detection for output time series of complex systems is one of the foremost problems in many fields of science. Especially in geomagnetism and magnetospheric physics, accurate detection of the dissimilarity between normal and abnormal states (e.g., pre-storm activity and magnetic storms) has the potential to vastly improve space weather diagnosis and, consequently, support the mitigation of space weather hazards. Several studies have reported advances in this context by applying complex systems tools like scaling exponents, entropies, functional network analysis, or recurrence analysis to different types of observational data including geomagnetic indices, space and ground magnetometers (Balasis et al. 2006, 2008, 2009, 2011a, 2013, 2018, 2020; Consolini et al. 2021; De Michelis and Consolini 2015; De Michelis et al. 2016, 2017a, 2020, 2021; Dods et al. 2015, 2017; Donner and Balasis 2013; Donner et al. 2018, 2019; Papadimitriou et al. 2020; Tindale and Chapman 2016; Wing et al. 2022).
Herein we present specific aspects of geomagnetic variability (in both time and space) that have already been successfully addressed with complex systems methods. By utilizing a variety of complementary modern complex systems-based approaches, an entirely novel view on nonlinear magnetospheric variability is obtained. For example, nonlinear measures based on the analysis of recurrences of previous states (Marwan et al. 2007; Donner et al. 2011a, 2011b) have been successfully applied to studying low-latitude geomagnetic indices Dst and SYM-H along with characteristic variables of the solar wind (Donner et al. 2018, 2019; Alberti et al. 2020b). Specifically, the time-dependent coupling between the solar wind and the magnetosphere along with the relationship between magnetic storms and magnetospheric substorms is of paramount importance for space weather processes. However, the storm/substorm relationship is one of the most controversial aspects of magnetospheric dynamics (Gonzalez et al. 1994; Kamide et al. 1998; Sharma et al. 2003; Daglis et al. 2003). In order to further disentangle this relationship and the role of relevant solar wind variables as drivers and mediators, multivariate causality measures employing the concept of graphical models constitute one particularly promising tool (Runge et al. 2015, 2019a). Toward this goal, in a recent article Runge et al. (2018) highlighted the significant potential of combining a causal discovery algorithm with a conditional independence test based on conditional mutual information for tackling contemporary research questions in magnetospheric physics, such as the storm-substorm relationship. Accounting for possible interactions between processes at different temporal scales, the aforementioned approaches can be combined with a recently developed framework for studying cross-scale interdependencies in complex dynamics (Paluš 2014).
Taken together, the multiplicity of recently developed approaches in the field of nonlinear time series analysis offers great potential for uncovering relevant yet complex processes interlinking different geospace subsystems, variables and spatio-temporal scales. Nowadays, information science and dynamical systems theory play a fundamental role in understanding and predicting the behaviour of the coupled solar-terrestrial system (Baker 2020). Therefore, this review provides a first-time systematic overview of relevant complex systems-based techniques and their applicability in the context of geomagnetic variability. Section 2 presents some particularly valuable concepts of dynamical systems theory, while Sects. 3 and 4 concentrate on substorm and storm research, respectively. Section 5 deals with the solar wind driving of radiation belt dynamics, while Sect. 6 provides a perspective on how systems science methodology can be further used to advance physical understanding of the near-Earth electromagnetic environment. The review concludes with an outlook.
2 Dynamical Systems Theory: Core Concepts and Their Practical Application
2.1 Dynamical Systems Theory, Statistical Physics and Chaos
Dynamical Systems Theory originated in Newtonian mechanics and has emerged as a universal approach to investigate the time evolution of a vast range of systems in physics, chemistry, biology, engineering and economy (Strogatz 2018; Contopoulos 2002), to name just a few. In general, a set of variables, each denoting a particular property, characterizes the instantaneous behaviour of the system. For example, a simple pendulum can be fully described by two parameters, its angular position and angular velocity. This set of variables represents the state of the system and the total number of such variables is called the number of degrees of freedom. All possible states of a system construct the state space, the dimension of which is equal to the number of degrees of freedom. In fact, at every time step, each state is represented by a point in the state space and its temporal evolution can be viewed as a sequence of states in this space, called the system trajectory. In many cases, the trajectory brings the system into a particular state or a set of states (a region in the state space) in long time, known as the attractor of the system. An attractor can be a fixed point, in which the system reaches an equilibrium state, or a limit cycle indicating a final stable oscillatory situation. However, sometimes the system can also end in a non-oscillatory motion within a complex-shaped set in the state space known as a strange attractor. Such systems are locally unstable yet globally stable.
The most common way to describe how the system state evolves is a set of continuous or discrete differential equations (also distinguished by the nomenclature of differential and difference equations, respectively), based on the governing laws among system variables. This also requires knowing the initial conditions (state) of the system. In principle, given the initial conditions (present state), one can predict the long-time behaviour (future states) of the system, deterministically. However, this may only be feasible for low-dimensional cases, i.e., systems with small numbers of degrees of freedom. In fact, in high dimensional systems with large numbers of degrees of freedom, like almost all real-world systems, one cannot solve such high dimensional equations of motions in practice.
One of the most successful theoretical frameworks of physics that deals with such high dimensional cases is statistical mechanics. Indeed, due to the incomplete knowledge of the microscopic world there should be some uncertainty in the system behaviour, thus bringing probability theory and statistics as well as entropy as a generic concept to quantify this uncertainty to the front. As a consequence, one can describe the (average) macroscopic behaviour of the system in terms of microscopic properties. In this approach, instead of working with a single state, one deals with a large number of copies of the system in its different possible states, referred to as a statistical ensemble of the system. This probabilistic point of view has helped us to investigate and understand a multitude of phenomena in nature, from the behaviour of elementary particles (Kardar 2007) to Earth and space sciences (Consolini et al. 2008; Balasis et al. 2013; Livadiotis 2018) and beyond.
Note that many concepts introduced in statistical physics are only applicable in equilibrium situations, in which the statistical ensembles are time independent. However, almost all real-world systems are changing over time, and exchanging mass and energy with their environment, i.e., they are open systems. Although non-equilibrium statistical physics can deal with many non-equilibrium systems, still many natural systems are far beyond the domain of non-equilibrium statistical physics. The seminal works of Einstein (Einstein 1905) and Langevin (Langevin 1908) on Brownian Motion introduced another probabilistic approach to overcome the high dimensionality of the system, especially in non-equilibrium situations. In this methodology, one focuses only on a few relevant and useful variables, and considers the effect of all other unknown dynamical variables as a noise, i.e. a stochastic term, and implements this into differential equations among those small number of variables. These types of equations are called stochastic differential equations and have found their applications in many research fields including physics, engineering, economics and finance, biology and medicine (Mao 2007). Such a stochastic point of view implies that any prediction about the system’s future evolution is also probabilistic.
The main problem here is that we usually do not know the noise term and hence need to make some assumptions about the nature of the noise. The validity of our assumptions usually can be verified by the comparison between our predictions and the experimental observations. Another possible source of stochasticity is the noise that arises from inaccurate measurements. In such cases, we can also implement the role of such observational noises into the corresponding dynamical equations, as mentioned above. Note that, instead of solving the stochastic dynamical equations between different system parameters, one can study the evolution of the probability density function of those parameters, by solving a deterministic differential equation, called Fokker-Planck equation (Kadanoff 2000) or, more generally, the Chapman-Kolmogorov equation (Kolmogorov 1938). This means that, the stochasticity aspect of the dynamics is inherited in the probability density that can give us remarkable information about the system dynamics, though in most nonlinear problems solving the Chapman-Kolmogorov or Fokker-Planck equation is almost impossible and one can only approximate the probability density, at best. This kind of stochastic approach has already found application in a broad range of research areas, such as climate modeling (Hasselmann 1976) and space physics (Subbotin et al. 2010; Noble and Wheatland 2012).
On the other hand, the lack of precise knowledge about the initial conditions can be another source of (apparent) stochasticity in the system’s behaviour, and thus be the source of unpredictability even in low-dimensional deterministic systems. This arises from the high sensitivity of the system dynamics to its initial conditions, in which a small uncertainty in the initial states, such as those due to errors in measurements or rounding errors in numerical calculations, often grow exponentially with time. This divergence of initially close trajectories in long time can be characterized by a quantity called Lyapunov exponent that measures the rate of this separation. This divergence means that the long-time behaviour of the system is unpredictable in general without the presence of any stochastic elements in its dynamics. Such behaviour is characteristic of nonlinear dynamical systems and classified as chaotic behaviour in which the system eventually reaches a strange attractor. Many physical, social, biological and economic systems are examples of such chaotic behaviour (Tsonis 1992), with many applications in climate and space sciences (Chen and Palmadesso 1986; Crosson and Binder 2009). Although many systems have been identified as examples of low-dimensional deterministic chaos, using various methods which estimate chaos-based parameters like dimension, number of degrees of freedom and Lyapunov exponents from experimental time series (Nicolis and Nicolis 1984; Fraedrich 1986; Tsonis and Elsner 1988), however, many of these findings were challenged. For instance, it has been shown in atmospheric dynamics that the reliability of such chaos-identification algorithms is limited and the observed low-dimensional weather or climate attractors have been considered as spurious results (Grassberger 1986; Lorenz 1991; Paluš and Novotná 1994). It asserts that the application of chaos-based measures like fractal dimensions or Lyapunov exponent can be unreliable in high dimensional or stochastic processes. After the critical re-evaluation of concepts based on purely deterministic systems, various types of information-theoretic measures have been proposed.
In the following, we will detail some fundamental concepts of dynamical systems theory and nonlinear time series analysis that have recently proven useful for gaining deeper insights into the nonlinear dynamical characteristics of the near-Earth electromagnetic environment.
2.2 Stochastic Time Series Properties: Long-Range Dependence, Fractals and Multi-Fractals
Long-range dependence is a wide-spread feature of real-world dynamical systems. By definition, it is associated with a linear time series analysis concept, the characteristic behaviour of a signal’s autocorrelation function (exhibiting power-law decay for many real-world geophysical systems) or, equivalently, the associated power spectral density (also displaying a characteristic power-law scaling), both of which are intimately related via a simple Fourier transform. While the scaling behaviour of the autocorrelation function is generally hard to identify for time series of limited length, the corresponding behaviour of the spectral density provides an easy and robust means to estimating a characteristic quantity, the power spectral exponent \(\beta \). This exponent is intimately related to another classical measure of long-range dependence, the celebrated Hurst exponent \(H\) originally introduced by the British hydrologist E.E. Hurst in the 1950s, via \(\beta = 2H+ 1\). In the context of river discharges, it has been argued that long-range dependence is naturally generated when superimposing various “microscopic” (stochastic) processes with heterogeneous parameters, or, alternatively, by performing a fractional-order integration of an input signal as a kind of nonlinear filter. Besides the power spectral density, various types of other nonlinear scaling characteristics have been suggested for estimating \(H\), including rescaled-range and detrended fluctuation analysis as two widely employed examples. A systematic inter-comparison between the three aforementioned techniques can be found in Witt and Malamud (2013).
The observation of long-range dependence in stochastic processes is related to a statistical self-similarity property of the time series graph, which is characterized by another scaling exponent measuring the roughness of this object in two-dimensional space as the scale of resolution is successively varied. Estimators of this scaling exponent quantify a fractal dimension \(D\) from a univariate stochastic process perspective, since their definition relies on fundamental concepts from fractal geometry. In the case of self-similar time series and the absence of heavy-tailed probability distribution functions, one finds another straightforward relationship between fractal dimension and Hurst exponent as \(D + H = 2\). There exist various approaches for estimating \(D\) from a univariate time series, including box-counting approaches, the Higuchi fractal dimension (Higuchi 1988), and Katz fractal dimension (Katz 1988), to mention only a few common examples. It should be noted, however, that the concept of a fractal dimension of the time series graphs, although rooted in fractal geometry, is intimately related with the linear time series property of power spectral density, and hence may not necessarily provide further insights into the studied signal beyond the latter. In essence, estimates of the Hurst exponent and the fractal dimension of the time series graph can be used interchangeably as long as there are no further complications like heavy-tailed probability distributions as commonly associated to intermittency. By contrast, in case of intermittent signals often encountered in space physics, both concepts actually provide complementary information.
2.3 Phase Space Based Methods
The aforementioned concepts of univariate time series analysis consider an observational time series as a unique source of information whose statistical properties exhaustively characterize the system under study, which however will typically be characterized by far more degrees of freedom than just one variable. In order to account for this fact, the concept of attractor reconstruction by embedding has become a core approach in dynamical system theory. Rooted in deep mathematical arguments, embedding theorems imply that under relatively general conditions, the action of unobserved variables of deterministic dynamical systems can be qualitatively reconstructed by deriving independent coordinates from a univariate time series, which are most commonly provided in terms of so-called delay coordinates, i.e. exact time-shifted replications of the original data sequence (Takens 1981). Accordingly, an \(m\)-dimensional state vector \(X\) can be reconstructed from scalar time series \(x ( t )\) as \(X ( t ) =[x ( t ),x ( t-\eta ),\dots ,x ( t- ( m-1 ) \eta ) ]\), where \(\eta \) is the backward time-lag that can, for example, be estimated from the first minimum of the mutual information (Fraser and Swinney 1986). In general, this time shift (embedding delay) and the number of shifts (embedding dimension \(m\)) should be chosen such that the individual coordinates are sufficiently independent and their entirety spans a multi-dimensional vector space in which the information contained by the original time series is completely unfolded among the different dimensions.
Utilizing the multivariate time series originated from time delay embedding, we can characterize the geometric properties of the system under study in the reconstructed phase space. There exist multiple complementary approaches to obtain useful information from this geometric perspective.
In the 1980s, in the field of dynamical systems, and in parallel also in the framework of fluid turbulence, different measures of complexity and scale-invariant features of physical systems have been introduced. They are mainly based on the concept of scaling, recalling the definition of a fractal, i.e., a geometric object displaying self-similarity and fine structure at small scales. These measures, usually called fractal dimensions, account for how the details change with the scale we are looking for. From a mathematical point of view, fractals are described via the scaling properties of a partition function based on a coarse-grained invariant measure in the probability space. Specifically, if we have a support \(\varOmega \) and we define a positive measure \(\mu \) (usually the probability of finding a portion of the state space filled by points), the partition function \(\varGamma (\ell)\) is defined as
that, in the limit of \(\ell\rightarrow 0\) displays a scaling-law behavior as
with \(D\) being the so-called fractal or box-counting dimension and \(B_{x} (\ell)\) a box of size \(\ell\) centered at \(x\). The latter formalism be generalized to any statistical order \(q\) such that
where the \(D_{q}\) are called generalized fractal dimensions, accounting for the correlation integrals of \(q\)-tuplets of points in the state space. In detail, \(D_{0}\) is the fractal (capacity or box-counting) dimensions, \(D_{1}\) is the information dimension, while \(D_{2}\) is the correlation dimension, accounting for the minimum number of system variables required to reconstruct the full dynamics of the system in its phase space. The box dimension \(D_{0}\) informs us on the geometrical features of the phase-space, indicating the minimum number of independent directions to be taken into account for confining the phase-space in a given geometrical shape. In the case of self-similar signals it relates to the Hausdorff dimension and to the Hurst exponent, informing us on the persistence/anti-persistence nature of the system. The information dimension \(D_{1}\) is a measure of the randomness of the distribution of points in the phase-space, strictly linked to the concept of loss of information, i.e., for how long the system can be accurately predicted. The correlation dimension \(D_{2}\) instead is a measure of the minimum number of variables (i.e., degrees of freedom) needed to properly describe the system.
If all \(D_{q}\) take the same values, we call the system under study mono-fractal, otherwise multifractal. Multifractal dynamics often co-occurs with intermittency phenomena, which are rather typical in space physics (e.g. the solar wind).
Another way to exploit the geometric properties of the multidimensional trajectory in the reconstructed phase space is studying the recurrence patterns of previously visited states in time. Here, recurrence refers to the close encounter of a previous state \(x\), typically defined as two states on the trajectory having a spatial distance smaller than some predefined threshold \(\varepsilon \). This concept of recurrence defines a binary relation between pairs of state vectors that can be visualized in terms of a so-called recurrence plot (Eckmann et al. 1987), where the morphology and statistics of patterns consisting of recurrent pairs can be used for defining a variety of complexity measures that can serve as proxies for predictability, determinism or laminarity, to mention only a few (Marwan et al. 2007). The density of recurrent pairs in dependence of \(\varepsilon \) corresponds to the aforementioned correlation integral, and its characteristic scaling exponent provides an estimator for the correlation dimension \(D_{2}\). In addition, it has been shown that characterizing the geometry of recurrent state pairs in the multidimensional phase space in terms of the topological characteristics of the resulting random geometric graph (Donner et al. 2011b; Donges et al. 2012) results in additional useful measures of complexity, which have been successfully employed in past studies to differentiate between the nonlinear fluctuation characteristics of geomagnetic indices during magnetic storms and quiescent periods (Donner et al. 2018, 2019).
While previous fractal dimension estimates have been based on the concept of scaling in phase space, in recent years, based on the concept of recurrences, Lucarini et al. (2012) introduced two dynamical systems metrics. One is the instantaneous dimension \(d\), accounting for the active number of degrees of freedom, and the other is the inverse persistence \(\theta \), measuring the short-term stability of the state space trajectory. Let us assume to have a trajectory in the state space \(x(t)\) and \(x(t^{*})\) to be a reference state of the system, i.e., a given configuration of the near-Earth electromagnetic environment (as an example, the quiet magnetosphere). If we define \(g(t^{*})\) as the Euclidean distance between \(x(t)\) and the reference state \(x(t^{*})\), the probability of logarithmic returns in a sphere centered at \(t^{*}\) and of radius \(r\) is a generalized Pareto-like distribution whose parameters are directly linked with \(d\) and \(\theta \). In the context of near-Earth electromagnetic environment studies these metrics have been employed by Alberti et al. (2022) to investigate the recurrence statistics of the AL and SYM-H indices. The main result is the clear dependence of the number of active degrees of freedom on the geomagnetic activity. In particular, during substorms the number of degrees of freedom increases at high latitudes; conversely, during a geomagnetic storm low-latitude exploits a reduced number of degrees of freedom. These two opposite behaviors can be related to the fast relaxation processes occurring in the magnetotail and the solar wind driving effect.
2.4 Information-Theoretic Approaches
Usually, temporal recordings of some system observables are our only asset to study the system of interest. Such time series may be univariate in the scalar case or multivariate when we deal with more than one observable. The aim is to understand the underlying dynamics of the system by analysing such deterministic or stochastic time series and extracting information from them. To quantify their inherent information content, a wide range of information-theoretic measures have been introduced. Univariate measures usually try to characterize the complexity of the dynamics like Shannon entropy (Shannon 1948) that shares the formalism with the Boltzmann-Gibbs entropic form, Renyi entropy (Rényi 1961), nonextensive entropy (Havrda and Charvát 1967; Daróczy 1970; Cressie and Read 1984; Tsallis 1988), Fisher information, Approximate entropy, Sample entropy and Fuzzy entropy (Balasis et al. 2013). However, in multivariate time series, one can ask whether different dynamical variables evolve independently or are mutually dependent, or whether one variable can influence other variables of the system. Studying such dependencies between different variables is also an important area of research, and can be related to questions of correlation and causality.
2.4.1 Entropies and Measures of Complexity
In spite of the immense success of many nonlinear time series analysis approaches with their broad range of applications, they often suffer from the domain of their applicability and their necessary assumptions, such as equilibrium-nonequilibrium, stability-instability, linearity-nonlinearity conditions, etc. As we mentioned before, entropy as a measure of the amount of uncertainty in statistical physics, has proved itself as significant in understanding various systems. In 1948, Shannon introduced a similar statistical concept to investigate the information size of a transmitted message (Shannon 1948), called information or Shannon entropy. For a discrete random variable \(X\) with a set of values \(\varXi \), the Shannon entropy \(H ( X )\) is defined as
where \(p ( x ) = \operatorname{Pr}\{X=x\}\), \(x \in \varXi \) is the probability distribution function of \(X\). Since this information entropy is not constrained by the aforementioned particular assumptions needed to study the underlying dynamics of a system, it opened new paths of research and played a significant role in the introduction of new statistical techniques (Kullback 1997). In the late 1950s, Kolmogorov and Sinai demonstrated that using the information theory of Shannon, a nonlinear dynamical process can be characterized by an entropy measure called the Kolmogorov-Sinai entropy (KSE). This entropy is suitable for classification of dynamical systems and is related to the sum of the positive Lyapunov exponents of the system and indicates that a nonlinear dynamical system can be represented as an information source (Billingsley 1965). Thus, information-theoretic measures may help to better understand dynamical processes. Indeed, as information can be representative of any physical quantities, the language of information theory proves to be powerful in investigating different complex dynamical systems (Brillouin 2013).
Renyi entropy (Rényi 1961) is a generalization of the Shannon entropy, defined as
where \(q\) is a real parameter characterizing the weights of rare and frequent events, allowing for scaling analysis of the system. Note that the Shannon entropy is a special case of \(H_{q}\) for \(q \rightarrow 1\). For example, Von Bloh et al. (2005) investigated the long-term predictability of global mean daily temperature data using the spatial patterns of the second order Renyi entropy \(H_{2}\).
The most generalized and physically constistent nonextensive entropy follows the formulation of Havrda and Charvát (1967), Daróczy (1970) and Tsallis (1988), which may be found as nonextensive, Tsallis, \(q\)-, or kappa entropy, can be considered as a generalization of the Boltzmann-Gibbs entropy in statistical physics, and is defined as follows:
where \(k\) is a positive constant that includes the Boltzmann’s constant, and \(q\) is a real parameter that characterizes the degree of non-extensivity. For \(q \rightarrow 1\) one can recover the Boltzmann-Gibbs entropy, which is a thermodynamic analogy of the Shannon entropy. Tsallis entropy has been widely applied in various fields of research (Tsallis 2009). For example, Balasis et al. have applied nonextensive entropy to quantify dynamical complexity of magnetic storms and solar flares (Balasis et al. 2011b) and of time series of the disturbance storm time index (Balasis et al. 2008).
In 1925, Fisher introduced a measure of the amount of information that can be obtained from a set of measurements (Fisher 1925), called Fisher information. One can write the Fisher information in the discrete form as
where \(x_{n}\) is the random variable \(X\) at time \(n\), \(p ( x_{n} )\) is its probability and \(N\) is the total number of time steps. Fisher information has proved itself as a powerful method to study various non-stationary and nonlinear time series (Martin et al. 1999). For example, it has been used to detect dynamical complexity changes associated with geomagnetic jerks (Balasis et al. 2016).
To compare deterministic and stochastic systems, Pincus introduced a new statistic for experimental time series, called approximate entropy, which is a parameter that measures correlation or persistence, i.e., low values of approximate entropy indicates that the system is very persistent, repetitive and predictive, while high values represent high randomness (Pincus 1991). Sample entropy is a modification of the approximate entropy, proposed in Richman and Moorman (2000). Both approximate and sample entropy have been used in various fields. For example, they have been applied in Balasis et al. (2013) to extract the complexity dissimilarity between different states of the magnetosphere.
Fuzzy entropy is a non-probabilistic concept that quantifies unpredictability of a time series. Fuzzy entropy is a measure of fuzzy information of a fuzzy system which is quite different from the Shannon entropy which is based on probability. Indeed, the uncertainty in fuzzy entropy arises from fuzziness, in contrast to the Shannon entropy where the uncertainty comes from the randomness (Al-Sharhan et al. 2001). Fuzzy entropy can be written as
where \(\mu _{i}\) is the \(i\)-th Fuzzy membership function. Similar to approximate and sample entropies, Balasis et al. also successfully applied Fuzzy entropy to extract the complexity dissimilarity among different magnetosphere states (Chen et al. 2007, 2009; Balasis et al. 2013).
If applied to simple state discretizations of a univariate time series, the aforementioned entropy concepts characterize merely higher-order distributional properties. This changes distinctively if state definitions are taken into account that explicitly include some type of dynamical perspective, e.g. by studying blocks of discretized states (Ebeling and Nicolis 1992) or their ordinalpatterns (Bandt and Pompe 2002). From the scaling of entropic characteristics with increasingpattern length, it is possible to distinguish complex deterministic from stochastic dynamics. Moreover, there exists a vast range of statistical complexity measures that can be defined using entropy concepts. Combining entropy and associated complexity characteristics in a two-dimensional plain (e.g. the complexity-entropy causality plain or the Shannon-Fisher plain) provides an effective means to distinguish chaos from stochastic motion (Rosso et al. 2007, Ribeiro et al. 2017).
2.4.2 Information Theoretic Measures of Statistical Association
The classical cross-correlation function provides a standard way to measure the similarity between the time series of two variables \(x(t)\) and \(y(t)\). We first define the time series \(\delta x ( t ) =x ( t ) - \overline{x}\) as the deviation from the time average (indicated by the horizontal bar; similarly for \(y(t)\)). Also the standard deviation of \(x(t)\) is given by \(\sigma _{X} = \sqrt{\overline{(\delta x)^{2}}}\). Then the correlation function is
Note that the correlation is a function of the lag \(\tau \) of time series \(y(t)\) in reference to time series \(x(t)\). While this fundamental measure is restricted to linear dependencies between the two variables, several information-theoretic measures have been developed to provide thorough generalizations, including mutual information, conditional mutual information and transfer entropy.
The average amount of common information, contained in two random variables \(X\) and \(Y\), is quantified by the mutual information \(I ( X;Y )\), defined as
where \(H ( X,Y ) =- \sum_{x \in \varXi} \sum_{y \in \Upsilon} \log p ( x,y ) \log p ( x,y )\) is the joint entropy and \(p ( x,y )\) is the joint probability density function of \(X\) and \(Y\). Thus, by substituting the definitions of \(H ( X )\) and \(H ( X,Y )\) in \(I ( X;Y )\), one gets
which is an average over \(\log \frac{p ( x,y )}{p ( x ) p ( y )}\). This indicates that if two variables \(X\) and \(Y\) are independent, i.e., \(p ( x,y ) =p ( x ) p ( y )\) then the mutual information \(I ( X;Y )\) tends to zero. In other words, if \(X\) and \(Y\) are dependent, then \(I ( X;Y ) >0\). In fact, \(I ( X;Y )\) can be considered as a generalized measure of (cross) correlation between two variables \(X\) and \(Y\) since, unlike the common correlation measures that are only able to detect linear dependency, mutual information is capable of capturing the general dependency among variables, including non-linear statistical associations. Note that \(I ( X;Y )\) is a symmetric measure under the exchange of \(X\) and \(Y\) and thus cannot be used as an appropriate causality measure straight away.
Paluš (1996) introduced an information theoretic measure for classification of complex time series based on auto-mutual information, characterizing the decay of \(I [ x ( t );x ( t+\tau ) ]\), called coarse-grained entropy rates. This measure quantifies the mutual information between time series \(x\) at time \(t\) and its time-lagged version, i.e., \(x\) at time \(t+\tau \) for a time lag \(\tau >0\). This measure can be considered as a relative measure of regularity and predictability and also is related to Kolmogorov-Sinai entropy for dynamical systems processes. For instance, it has been used to classify some physiological signals like electroencephalography (EEG) and tremor (Paluš 1996).
By investigating the entropy rate of a Gaussian process, Paluš (1997) developed a measure capable of distinguishing and characterizing different states of chaotic dynamical systems, called Gaussian process entropy rate. This is indeed a power-spectrum based entropy-like functional and is related to the Kolmogorov-Sinai entropy of a dynamical system. Such an entropy rate has been applied in meteorological time series to extract the system complexity (Paluš et al. 2011), for example.
2.4.3 Causality Among Time Series
A popular information-theoretic functional used for inferring causality under appropriate assumptions is the conditional mutual information (CMI) \(I ( X;Y \vee Z )\) of the variables \(X\) and \(Y\) given the variable \(Z\), defined as
If \(Z\) is independent of \(X\) and \(Y\), then \(I ( X;Y \vee Z ) =I ( X;Y )\), demonstrating that \(I ( X;Y \vee Z )\) extracts the net shared information between \(X\) and \(Y\) beyond the information of another variable \(Z\). In order to extract the possible time-delayed relationships among different variables, one should work with time delayed versions of the abovementioned measures. For example, if there is a time delay \(\tau \) between the two variables \(X\) and \(Y\), one can define a time-delayed mutual information as \(I [ X ( t );Y ( t+\tau ) ]\), which measures the average amount of information contained in the process \(X\) about the \(\tau \)-future of the process \(Y\). However, there is also information about the \(\tau \)-future of \(Y\) contained in \(Y\) itself, if \(X\) and \(Y\) are not independent. In this respect, the net information about the \(\tau \)-future of the process \(Y\) which is contained in the process \(X\) can be obtained by the conditional mutual information \(I [ X ( t );Y ( t+\tau ) \vee Y ( t ) ]\) (Paluš et al. 2001). This measure can extract the coupling direction in bivariate dynamical systems and indeed is a nonlinear generalization of the Granger causality (Granger 1969). Schreiber (2000) introduced a measure using the idea of finite-order Markov processes known as the transfer entropy, which is an equivalent expression for the time-delayed conditional mutual information defined above.
Note that in empirical experiments usually only one possible dimension of the phase space is observed for each system. In such situation, by drawing upon phase space reconstruction by means of time delay embedding, the time-delayed CMI defined above can be reformulated as
where \(\eta \) and \(\rho \) are time-lags used for the embedding of variables \(X ( t )\) and \(Y ( t )\), respectively. Note that here only the information about a single component of \(y ( t+\tau )\) in the \(\tau \)-future of the system \(Y\) is used for simplicity. Further extensive numerical analysis (Paluš and Vejmelka 2007) suggest that often a CMI in the form
is sufficient to extract the direction of coupling among \(X ( t )\) and \(Y ( t )\), i.e., the dimensionality of the condition must contain full information about the state of \(Y ( t )\), while single components \(x ( t )\) and \(y ( t+\tau )\) are able to provide information about the coupling direction from \(X\) to \(Y\), denoted as \(X \rightarrow Y\). Simply, one can obtain the causal link \(Y \rightarrow X\) as
However, Paluš (2014) criticized that, in general, the prediction horizon \(\tau \) in such equations cannot well demonstrate a time-delayed coupling. Wibral et al. (2013) proposed a solution by a simple reformulation as
Under certain assumptions (Runge et al. 2019a) these measures can detect the presence of causal relationships. In Runge et al. (2019b) a systematic causal discovery algorithm for time series has been presented that can be used together with conditional mutual information. This algorithm was generalized in Runge (2020) to also detect instantaneous causal relations, and in Gerhardus and Runge (2020) to also account for hidden common causes. These methods have great potential for further studies of causal relations among geomagnetic processes.
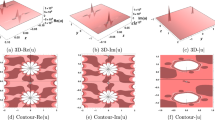
As an example, the conditional mutual information has been applied to investigate the causal information transfer between solar wind parameters and geomagnetic indices (Manshour et al. 2021). Specifically, in order to find the causality directions as well as the presence of any information transfer delay between the solar wind and the geomagnetic indices, the conditional mutual information was estimated between the vertical component of the interplanetary magnetic field \(B_{z}\) as a solar wind parameter and two well-known geomagnetic indices representing the auroral electrojet (AE), a substorm index, and the SYM-H, a storm index, using \(\rho =5\) samples (25 min) and \(n=3\) as the embedding parameters. In order to compute the statistical significance of those calculations, the circular time-shifted surrogates test was applied by comparing the empirical results with the average values of a set of 100 different realizations of the surrogates (Manshour et al. 2021).
Figure 1(a) demonstrates that a strong causal link exists from \(B_{z}\) to AE and also the information transfer takes two sample time steps (10 min). However, Fig. 1(b) indicates that there is no causal relationship from AE to \(B_{z}\). Similarly, we plotted CMI for the time series of \(B_{z}\) and SYM-H in Fig. 1(c) and (d). Figure 1(c) indicates that a causal relationship also exists from \(B_{z}\) to SYM-H; and the information transfer takes six sample time steps (30 min). Also, there is no causality in the reverse direction, as represented in Fig. 1(d). Our findings confirm that the interplanetary magnetic field component \(B_{z}\) drives both geomagnetic storms and substorms with different delays. The response time for the magnetic storms is longer than the time delay among the solar wind energy input and the energy release in the magnetotail during a substorm (Maggiolo et al. 2017) since it takes a considerably long time to inject particles into the ring current region (Daglis et al. 1999).
(Fig. 3 from Manshour et al. 2021) The coupling directions of (a) \(Bz\rightarrow AE\), (b) \(AE\rightarrow Bz\), (c) \(Bz\rightarrow SYM-H\), (d) \(SYM-H\rightarrow Bz\), (e) \(AE\rightarrow SYM-H\), and (f) \(SYM-H\rightarrow AE\). (g) and (h) are the coupling directions similar to (e) and (f), by taking \(B_{z}\) as the common driver. Also (i) and (j) are the coupling directions similar to (c) and (d), by taking AE as the common driver. The red lines and error bars present mean and ±2 standard deviations of CMI for a set of 100 circular time-shifted surrogates
The presence of any possible causal relationship between substorms and storms has been an open and challenging debate in space weather studies. Here, to analyze the presence of information flow between the geomagnetic indices, we further plotted in Fig. 1(e) and (f) the CMI of AE and SYM-H. Figure 1(e) shows that there is a strong flow from AE to SYM-H; which means that geomagnetic storms are driven by substorms without any delay. No information flow is detected from storms to substorms, as can be seen in Fig. 1(f). This result is indeed in line with some previous studies (Stumpo et al. 2020; Ganushkina et al. 2005). However, we demonstrate that the observed causality in Fig. 1(e) is not a direct causal link, and it indeed arises according to the presence of the common driver \(B_{z}\). To show this, we consider the effects of this common driver in CMI calculations. We can simply include \(B_{z}\) as the third variable into the condition, as
Figure 1(g) and (h) represent this CMI, and interestingly we discover that there is no information flow between AE and SYM-H when eliminating the role of the common driver \(B_{z}\). Furthermore, we also check the possible role of AE on the observed information flow among \(B_{z}\) and SYM-H, by interchanging the variables of \(B_{z}\) and AE. Figure 1(i) and (j) asserts that the information flow of \(B_{z}\) into SYM-H is independent of the AE index. Briefly, our results suggest that the observed information flow from geomagnetic substorms into storms is induced by the common solar wind driver \(B_{z}\) and in fact, there is no causal relationship between substorms and storms, which is in agreement with some previous studies (Gonzalez et al. 1994; Kamide et al. 1998; Runge et al. 2018). Runge et al. (2018) identified \(B_{z}\) and other confounders of AE and SYM-H by applying a systematic information-theoretic causal discovery algorithm. However, it should be noted here that in-situ observations have shown that the contribution of ion injections to the ring current energy gain is substantial, despite the fact that our results for the specific time scales considered and datasets examined do not favor the role of substorms in the enhancement of the storm-time ring current through accumulative ion injections during consecutive substorms (see also the references in Runge et al. 2018). Moreover, in contrast to our results, substorm bursty-bulk flows (BBFs) accompanied by strong convection may penetrate the inner magnetosphere and contribute to the ring current.
2.5 Time Series Decomposition
Physical systems and natural processes are usually characterized by a chaotic and unpredictable behaviour, typically displaying multiscale interacting components. This is manifested in the existence of some scaling-law behaviour, reflecting their (multi)fractal nature. Moreover, they are also characterized by bifurcations between different states, strange attractors, and invariant manifolds, reflecting the different dynamical regimes of the system. Thus, a first step towards characterizing these features relies on decomposition methods. These methods are usually classified into adaptive and non-adaptive/fixed-basis concepts: the latter presents a strong mathematical background, while the former detects structures embedded with no a priori assumptions.
2.5.1 Wavelet Analysis
Fourier transform (FT), a cornerstone of time series analysis, is a commonly used technique to convert a signal in time domain into a frequency domain representation by decomposing it in terms of sinusoidal components (basis functions) spanning the whole spectrum. FT captures only global frequency information, averaged over the entire time period of observations. Thus, if frequency components of a time series vary over time, FT cannot identify those localized features of the series. In order to capture the frequency information localized in time, one can find a sequence of FT of a windowed signal, known as short time Fourier transform (STFT). However, it still suffers from some limitations such as using a window of constant shape and size as well as non-localized sinusoidal basis functions, so that it cannot capture the characteristics of sharp events or those with different durations. On the other hand, due to the Heisenberg’s uncertainty principle, STFT cannot generate features with both time and frequency instantaneous localization.
Wavelet Transform (WT) tries to overcome the STFT shortcomings and is a powerful technique for analyzing localized variations of power within a time series (Addison 2017). Similar to STFT, WT is a method to convert a one-dimensional time domain signal into a two-dimensional time-frequency domain signal, but in contrast to STFT, the wavelet algorithm uses basis functions with transient nature, called mother wavelets, which are not restricted to a single family of functions (like sinusoidal functions in STFT) and have a wave-like nature that is localized in time, capable of locating the occurrence of a sharp event in the time domain. The wavelet functions can be obtained as a linear combination of scaled and shifted mother wavelets.
In general, a wavelet transform can be either continuous or discrete. At first, we briefly describe the continuous wavelet transform (CWT) algorithm. The function \(\Psi \) can be a mother wavelet if it satisfies two conditions. It must have zero-mean
and finite energy (or, equivalently, must be square integrable), i.e.,
As we mentioned above, a wavelet is constructed from a scaled and shifted mother wavelet \(\Psi \) as
where \(\theta \) and \(s\) are shift and scale parameters, respectively. In fact, \(\theta \) indicates the location of the wavelet in time and if \(s>1\) the wavelet is stretched along the time axis, whereas if \(0< s<1\), the wavelet is contracted. The CWT of a time series \(x(t)\) in a given location and scale can be obtained by projecting \(x(t)\) onto the corresponding wavelet as:
where (∗) indicates the complex conjugate. In fact, CWT provides the local similarity (or correlation) of a particular section of a signal and the corresponding wavelet, thus by changing the shift and scale parameters one can construct a two-dimensional picture representing the amplitude of any features versus the scale (or frequency) as well as the time resolution of this amplitude. If the mother wavelet also satisfies the admissibility condition of
where \(\tilde{\Psi} (\omega )\) denotes the Fourier transform of \(\Psi (t)\), one can reconstruct the original time series by using the inverse wavelet transform as
Another form of wavelet analysis is the discrete wavelet transform (DWT), in which the scale and shift parameters are discrete. For example, in the dyadic DWT the scale takes values of the form \(s= 2^{k}\) where \(k\) is an integer and at a given scale \(s\), the shift parameter takes values of the form \(\mu = 2^{k} l\) where \(l\) is also an integer number. Accordingly, discrete wavelets are defined as
The DWT of a signal \(x(t)\) is
The original signal \(x ( t )\) can also be reconstructed using the inverse wavelet transform as
if the discrete wavelets form an orthogonal basis, i.e.,
where \(\delta _{lk}\) denotes the Kronecker’s delta function. Due to the discrete nature of the parameters in the DWT, localization of transient features or characterization of oscillatory behaviours is much harder than in the CWT. On the other hand, only a restricted number of admissible wavelets are available in DWT when compared with CWT. However, the algorithm of DWT is simple and computationally more efficient than CWT.
Wavelet transform has widely been applied in science, engineering, medicine and finance (Addison 2017), and it has already proved itself as a powerful tool in geophysical research, including geospace disturbances (Katsavrias et al. 2022 and references therein), synchronization between wavelet modes of North Atlantic Oscillation index, the time series of sunspot numbers, the geomagnetic activity aa index and near surface air temperature (Paluš and Novotná 2009), the magnetic storm activity (Xu et al. 2008; Mendes et al. 2005; Wei et al. 2004), self-affine properties of geomagnetic perturbations (Zaourar et al. 2013), external source field in geomagnetic signals (Kunagu et al. 2013), seasonal variations in the Ap index (Lou et al. 2003), the effects of the interplanetary magnetic field polarities on geomagnetic indices (El-Taher and Thabet 2021), the interrelationship between solar wind coupling functions and the geomagnetic indices Dst and AL (Andriyas and Andriyas 2017), variation of relativistic electrons in the outer radiation belt (Katsavrias et al. 2021), and the causal relations between the magnetosheath pressure and the waves observed in the magnetosphere (Archer et al. 2013).
2.5.2 Singular Spectrum Analysis
Singular spectrum analysis (SSA) is a nonparametric and data-adaptive method that addresses a variety of problems in time series analysis including forecasting, imputation of missing values, and reducing the dimensionality by decomposing a time series into a small number of interpretable components such as trends, oscillatory behaviours and noise (Elsner and Tsonis 1996; Golyandina et al. 2001). SSA contains elements of signal processing, linear algebra, nonlinear dynamical systems, ordinary differential equations, and functional analysis (Golyandina et al. 2001). As a powerful tool for time series analysis, it has frequently been applied in a broad variety of fields such as oceanology (Colebrook 1978), meteorology and climatology (Ghil and Vautard 1991; Keppenne and Ghil 1992; Yiou et al. 1994; Allen and Smith 1994; Ghil et al. 2002), nonlinear physics and signal processing (Broomhead and King 1986), economy (Hassani and Zhigljavsky 2009), and social sciences (Golyandina et al. 2001) among others.
The fundamental step in SSA is an orthogonal decomposition of a covariance matrix of the studied time series into its spectrum of eigenvalues as well as its orthogonal eigenvectors. One obtains linearly independent individual data components (modes) by projecting original data onto these orthogonal eigenvectors. In fact, the basic univariate SSA steps can be described as follows: Let a univariate time series \(y_{i}\), \(i = 1,\ldots, N_{0}\), be a realization of a stationary and ergodic stochastic process \(\{ Y_{i} \}\). We map the original time series \(y_{i}\) into a sequence of \(d\)-dimensional lagged vectors of \(\boldsymbol{x}_{i}\) with components \(x_{i}^{k} = y_{i+k-1}\) where \(k=1,\dots ,d\) and \(i=1,\ldots, N= N_{0} -d+1\). The sequence of the vectors \(\boldsymbol{x}_{i}\) is usually referred to as the \(N\times d\) trajectory matrix \(\boldsymbol{X} =\{ x_{i}^{k} \}\), which contains the complete record of patterns that have occurred within a window of size \(d\) (embedding dimension). Suppose that the original time series \(y_{i}\) results from a linear combination of \(m< d\) different dynamical modes. Then, ideally, the trajectory matrix \(\boldsymbol{X}\) has rank \(m\), and can be transformed into a matrix with only \(m\) nontrivial linearly independent components. Instead of the \(N\times d\) matrix \(\boldsymbol{X}\), it is more appropriate to decompose the symmetric \(d\times d\) lagged-covariance matrix \(\boldsymbol{C} = \boldsymbol{X}^{T} \boldsymbol{X}\), since \(\boldsymbol{X}\) and \(\boldsymbol{C}\) have the same rank. If the components \(\{ x_{i}^{k} \}\) have zero mean, then the elements of the covariance matrix \(\boldsymbol{C}\) can be written as
where \(1/N\) is a normalization factor. The symmetric matrix \(\boldsymbol{C}\) can be decomposed as
where \(\boldsymbol{V} =\{ v_{ij} \}\) is an \(d\times d\) orthogonal matrix and \(\boldsymbol{\Sigma} \) is a diagonal matrix of elements \(\sigma _{1}, \sigma _{2},\ldots, \sigma _{d}\). The elements \(\sigma _{k}\), \(k=1,\dots ,d\) are the non-negative eigenvalues of \(\boldsymbol{C}\) by convention given in descending order \(\sigma _{1} \geq \sigma _{2} \geq \cdots \geq \sigma _{d}\). The square roots of the eigenvalues, \(\sigma _{k}^{1/2}\), and the set of \(\{ \sigma _{k}^{1/2} \}\) are called singular values and singular spectrum, respectively, and give SSA its name. Simply, one can calculate the modes as \(\xi _{i}^{k} = \sum_{l=1}^{d} v_{lk} x_{i}^{l}\). If the rank of \(\boldsymbol{C}\) is \(m< d\), then \(\sigma _{1} \geq \cdots\ \geq \sigma _{m} > \sigma _{m+1} =\cdots = \sigma _{d} =0\). In the presence of noise, however, all eigenvalues are positive and we have \(\sigma _{1} \geq \cdots \geq \sigma _{m} \gg \sigma _{m+1} \geq \cdots \geq \sigma _{d} >0\) (Broomhead and King 1986). In fact, if we plot the eigenvalues, \(\sigma _{k}\), one can often observe an initial steep decline for \(k=1,\ldots, m\) and a nearly flat line for \(k=m+1,\ldots, d\), thus the corresponding modes, \(\xi _{i}^{k}\), are considered as the signal part and the noise part, for the former and the latter case, respectively. In this respect, the signal modes can be used to reconstruct the denoised signal \(\tilde{x}_{i}^{k}\) as
Analogously, the original time series \(x_{i}^{k}\) can be reconstructed back from the modes as
The modes \(\xi _{i}^{k}\) can also be considered as time-dependent coefficients and the orthogonal vectors \(\{ v_{l}^{k} \}\) as basis functions, also known as the empirical orthogonal functions.
As mentioned above, distinguishing the signal components from noise is based on finding a threshold to a noise floor. This approach might be problematic if the noise present in the data is not white but colored or the signal-to-noise ratio is not large enough. For example, in the presence of red noise of \(1/f\) type power spectra, which is ubiquitous in geophysical processes, one cannot reliably detect a nontrivial signal only by comparing the eigenvalues, since the eigenvalues related to the slow modes are much larger than those of the fast modes. Hence, the eigenvalues of the slow modes might incorrectly be interpreted as a nontrivial signal, or, on the other hand, a nontrivial signal embedded in a red noise might be neglected if its eigenvalues are smaller than the slow-mode eigenvalues of the background noise.
To correctly distinguish a signal from red noise, a statistical approach called Monte Carlo SSA (MCSSA) has been proposed that utilizes the Monte Carlo simulation techniques to test the eigenvalues of the SSA modes against a red noise null-hypothesis (Allen and Smith 1996). Surrogate data complying with this null-hypothesis are constructed as realizations of an autoregressive process of order 1, reflecting the \(1/f\) character of the analyzed data spectrum. For each realization, a covariance matrix \(\boldsymbol{C}_{r}\) is computed and then projected onto the eigenvector basis of the original data. The statistical distribution of the diagonal elements of the resulting matrix, obtained from the ensemble of Monte Carlo simulations, gives confidence intervals outside which a time series mode can be considered significantly different from a generic red-noise process. An extension of MCSSA has been proposed by Paluš and Novotna (2004) to evaluate and test regularity of dynamics of the SSAmodes against the colored noise null hypothesis, in addition to the test based on eigenvalues. This enhanced MCSSA has successfully been applied in detection of oscillatory modes in records of the monthly North Atlantic Oscillation index, the time series of sunspot numbers, the geomagnetic activity aa index and near surface air temperature from several mid-latitude European locations (Paluš and Novotná 2008, 2009).
The SSA algorithm has also been extended in order to analyse multivariate time series in the presence of noisy and/or missing data (Allen and Robertson 1996). Similar to the univariate SSA, decomposition and reconstruction are two main ingredients in multi-channel singular spectrum analysis (mSSA). Accordingly, the multivariate trajectory matrix \(\boldsymbol{D}\) is constructed as \(\boldsymbol{D} =( \boldsymbol{X}^{1},\dots , \boldsymbol{X}^{L} )\) where \(L\) is the number of time series and \(\boldsymbol{X}^{\boldsymbol{i}}\) represents the trajectory matrix of the \(i\)-th time series. Then, the grand lagged covariance matrix is obtained as \(\boldsymbol{C}^{{G}} = \boldsymbol{D}^{T} \boldsymbol{D}\). After finding the corresponding eigenvalues and eigenvectors of the decomposed \(\boldsymbol{C}^{G}\), one can compute the reconstructed components of the original time series similar to the basic SSA algorithm described above. mSSA is an effective statistical data analysis method and has been applied to various fields including oceanography, geoscience, meteorology, among others (Vautard and Ghil 1989; Wang et al. 2016; Shen et al. 2017; Zotov et al. 2016; Zhou et al. 2018).
2.5.3 Empirical Mode Decomposition
Recently, a wide range of adaptive methods have been proposed (Chatfield 2016) and also applied in the field of geospace research (e.g., Balasis and Egbert 2006; Alberti et al. 2017, and references therein). Among them, particular attention has been paid to the Empirical Mode Decomposition (EMD) (Huang et al. 1998; Huang and Wu 2008). EMD is an adaptive method based on an iterative process known as sifting that exploits the local properties of signals to derive the decomposition basis. Given a signal \(y(t)\), the sifting consists of the following steps:
-
1.
derive a zero-mean signal \(r(t) = y(t) - \langle y(t)\rangle \), with \(\langle \dots \rangle \) denoting the time average;
-
2.
derive the local maxima and minima of \(r(t)\) and interpolate them separately via cubic splines to derive upper \(u(t)\) and lower \(l(t)\) envelopes;
-
3.
evaluate the mean envelope \(m(t) = (u(t) +l(t))/2\) and determine the detail \(h(t) = r(t) - m(t)\);
-
a.
if the numbers of extrema and zero crossings are equal or differ at most by one and if the mean envelope of \(h(t)\) has a zero mean, then \(h(t)\) is assigned to be an Intrinsic Mode Function (IMFu) or empirical mode;
-
b.
otherwise steps 1 to 3 are iterated n times until a candidate detail \(h_{n}(t)\) is assigned to be an IMFu.
-
a.
Step 1. to 3. are repeated on the residual \(r_{h}(t) = r(t) - h_{n}(t)\) until no more IMFus can be extracted. In the end, the signal \(y(t)\) can be written as the sum of all empirical modes \(\{c_{k}(t)\}\) and the final residue \(r(t)\), e.g., a non-oscillating function, as
where \(N_{{k}}\) is the number of detected IMFus. The set of \(\{c_{k}(t)\}\) is the basis of a Hilbert space, satisfying properties of completeness, convergence, and local orthogonality (Huang et al. 1998; Flandrin et al. 2004).
An example of the intrinsic mode functions obtained via the EMD procedure is shown in Fig. 2 for the geomagnetic storm occurred on 22 August 2005. As expected, the amplitudes of empirical modes show an increase in correspondence of the three geomagnetic storms. However, the empirical modes associated with the shortest timescales, i.e., \(C_{1}(t) - C_{8}(t)\), show irregular amplitude enhancements also before/after the storms (see, e.g., the time period from 10 to 15 August 2005), suggesting that at these timescales the dynamics of SYM-H may be not directly controlled by the external driving, i.e., not linearly correlated to interplanetary changes. Indeed, according to Alberti et al. (2017) the fluctuations at these timescales do not show a one-to-one coupling with solar wind and interplanetary parameters, indicating the occurrence of a nonlinear response at these timescales (see, e.g., Tsurutani et al. 1990).
(Fig. 4 from Alberti et al. 2018) The empirical modes (\(C_{{k}}(t)\)) and the residue (\(\operatorname{res}(t)\)) extracted from the SYM-H time series for the time period from 10 August 2005 to 10 September 2005. The empirical modes are ordered by increasing characteristic timescale (from top to bottom)
Once the decomposition basis is obtained, the local amplitude-frequency modulation can be derived via the Hilbert Transform (HT) defined as
where \(P\) denotes the Cauchy principal value. By defining a complex signal as
with
where \(a_{k} ( t )\) and \(\phi _{k} ( t )\) are the instantaneous amplitude and phase of the \(k\)-th empirical mode, respectively, a time-frequency-amplitude representation can be derived, usually known as Hilbert-Huang spectrum, by contouring the squared instantaneous amplitudes in a time-frequency plane (Huang et al. 1998). By integrating over time, the so-called Hilbert marginal spectrum can be derived, strictly related to the Fourier power spectral density, accounting for the second-order statistical moment frequency distribution (Consolini et al. 2017). It should be noted though that estimating the exponents that characterize scaling is challenging in real-world data, and requires a methodology that goes beyond Fourier approaches (Kiyani et al. 2009, 2013).
An example of the Hilbert marginal spectrum obtained from the analysis of solar wind turbulence and small-scale dynamics is shown in Fig. 3 (Consolini et al. 2017). Two different spectral regimes, characterized by different spectral exponents, can be identified above and below the spectral break \(f_{b} \sim 0.3~\text{Hz}\). This frequency break is compatible with the ion cyclotron frequency \(f_{\varOmega}\) considering the effect of the Doppler shift. Furthermore, below the frequency break all the spectra tend to the typical magnetohydrodynamic (MHD) Alfvénic turbulence spectrum (\(S(f) \sim f^{- 3/2}\)), while above \(f_{b}\), i.e., in the kinetic domain, the spectra are approximately \({\sim} f^{- 8/3}\). This value seems to be compatible with several different kinetic turbulent regimes (e.g., compressible Hall-MHD turbulence, EMHD-turbulence, kinetic Alfvén wave turbulence), which predict a spectral slope near \({\sim}{-}7/3\).
(Fig. 6 from Consolini et al. 2017) The marginal Hilbert energy spectra in the parallel and perpendicular directions to the mean field
As a conclusion of this part, we would like to summarize some of the advantages and limitations of the EMD. It is particularly suitable to reduce a priori assumptions on the functional form of the basis of the decomposition, carrying out local features from time series that cannot usually be obtained by using fixed eigenfunctions. However, as for each data analysis method some outstanding problems need to be listed.
-
1.
End/Boundary effects occur since the sifting is based on the local extremes of the time series. End points of the latter are clearly classified as local extrema. This can produce misleading empirical modes, propagating into the decomposition process through the sifting steps, since they are not the extreme values of the time series. To avoid this problem mirror and/or data extending methods (Huang and Wu 2008) have been proposed for a better spline fit at the ends.
-
2.
Mode mixing can take place if a similar scale is present in different empirical modes. This is related to the signal intermittency, aliasing the time-frequency distribution and devoiding empirical modes of physical meaning (Huang et al. 1998, 1999). One of the ways to avoid this problem is a noise-assisted sifting, known as Ensemble EMD. It consists of adding an ensemble of white noise series to the original data and use the EMD to decompose each time series. Then, the true empirical mode is the ensemble mean of the corresponding intrinsic mode functions of the decomposition.
2.5.4 Multiscale Fractal Measures of State Space Trajectories
One of the most intensively studied contemporary problems in nonlinear sciences is the investigation of the multiscale dynamical properties of time series. Recently, the previously described EMD has been used in combination with state space indicators to investigate scale-dependent properties of physical systems. As shown in Alberti et al. (2020a) multiscale measures can be derived by looking at the generalized fractal dimensions at different scales retrieved via the EMD algorithm. Let us assume that a signal \(s ( t )\) could manifest a multiscale behaviour
where \(\langle s\rangle \) is a steady-state average value and \(\delta s_{\tau} ( t )\) a fluctuation at scale \(\tau \). For each \(\sum_{\tau} \delta s_{\tau} ( t )\) a natural measure \(d \mu _{\tau} \) can be introduced in a way similar to the concept of scale-local Rényi dimensions (Grassberger 1985) as follows. We first consider a partition function
with \(B_{s,\tau} ( l )\) being the hypercube of size \(l\) centered at the point \(s\) on the space of the \(\sum_{\tau} \delta s_{\tau} \). Thus, the multiscale generalized fractal dimensions can be introduced as
This approach, similarly to the partial dimensions proposed by Grassberger (1983), allows us to detect information on the state space topological properties by investigating the behaviour of the generalized dimensions at different scales \(\tau \). Furthermore, via the Legendre transform we can evaluate the multiscale singularities and singularity spectrum as
Figure 4 reports an exemplary application of this formalism to the analysis of the SYM-H geomagnetic index. It is interesting to observe the existence of a multifractal nature at all scales, although different values are found for the multiscale generalized fractal dimensions \(D_{{q, \tau}}\). Indeed, a more regular behaviour is found at long timescales, mainly related to the solar wind variability and to the nonlinear response of the magnetosphere to solar wind changes. Conversely, the short timescale dynamics, that can be related to the internal dynamics of the magnetosphere, is characterized by larger dimensions, reflecting a stochastic nature of fluctuations. Furthermore, by reconstructing the phase space we can underline two different regions: one corresponds to the quiet-time values of the SYM-H index and the other to the disturbed-time ones. By using the short-scale reconstruction of empirical modes it does not quite reproduce the phase space dynamics, suggesting that some relevant information is missed. By providing instead reconstructions of IMFs on large timescales we are able to cover those phase space regions which have not been captured by the fast component. This can be interpreted as a signature of the existence of a different origin of processes operating on short and long timescales.
(Fig. 14 from Alberti et al. 2020a) Multifractal analysis of the Dst index
2.6 Multiscale Stochastic Approaches in Geospace Research
Interpreting the geospace variability in terms of a dynamical system, whose dynamics spans a wide range of scales with a clear separation between fast and slow processes, is one of the most promising aspects for understanding and predicting its variations. In the simplest way a non-linear stochastic model, based on a generalized Langevin equation, could be feasible. This approach, extensively used in the climate framework (see, e.g., Ditlevsen 1999; Kwasniok and Lohmann 2009; Livina et al. 2010; Alberti et al. 2014), is based on a 1-dimensional system, described by a continuous system variable \(x ( t )\), whose slow dynamics is driven by a forcing term \(F ( x )\), while the fast dynamics is described in terms of a noise process \(\eta ( t )\) of amplitude \(\sigma \). The Langevin equation reads
where \(U ' ( x ) =-F ( x )\). From a dynamical system point of view, \(U ( x )\) captures all the statistical properties of the system, since it can be linked to the probability distribution function of the system variable \(x\). Indeed, in this case the Fokker-Planck equation now reads
In this case, the stationary solution for the probability distribution, \(p_{s} ( x )\), is a direct function of the state function \(U ( x )\), being
Then, once the stationary distribution function \(p_{s} ( x )\) is known, by inverting the above relation it is possible to get the state function \(U ( x )\) responsible for the slow dynamics as
The stationary solution is also an equilibrium solution (Ichimaru 1973), so that the state function \(U ( x )\) can be used to investigate the number and the nature of the available system states. Indeed, having even-order state functions (i.e., with positive curvature at both minus and plus infinity), the number of zero crossings of the first derivative of \(U ( x )\) corresponds to the number of system states, while the sign of the second derivative evaluated at the zeros of \(U ' ( x )\) characterizes their nature (positive: stable, negative: unstable) (Ditlevsen 1999; Kwasniok and Lohmann 2009; Livina et al. 2010; Alberti et al. 2014).
3 Contributions to Substorm Research
3.1 Nonlinear and System Science Approaches to Substorms
Substorms share basic characteristics with driven, dissipative systems that are far-from-equilibrium, and as such suggest points of contact with the wider field of non-equilibrium statistical physics. The magnetosphere is a driven system with capacity for mass, momentum and energy storage and release on multiple scales: (i) microscales, where an instability occurs in a background plasma that can be treated as approximately uniform, (ii) mesoscales, where the variation in the background is relevant, and (iii) macro- or system scales, there the process spans the entire magnetosphere, as in a geomagnetic substorm.
Many of the approaches and physical models that have been suggested for substorms have heritage in non-linear and complex systems modeling. We can chart the development of this strand of substorm research across three broad categories:
-
1)
Low-dimensional and in a smoothed sense deterministic
-
2)
High dimensional and intrinsically stochastic
-
3)
An emergent transition from a system dominated by processes on the micro and mesoscale, to one characterized by large scale system-spanning coherent structure
3.2 Low-Dimensional and Deterministic
Some of the earliest attempts to understand and model the substorm cycle are of this class. Baker et al. (1990a) suggested that the cycle of magnetotail loading and unloading maps onto the “dripping faucet” of Shaw (1984). The water drip from a slowly leaking faucet will always eventually produce a disconnected droplet of water, but the exact time of disconnection, and size of droplet, is highly uncertain as it appears to behave as a chaotic system. An analogue is the formation of a near-Earth neutral line or the disconnection of the magnetotail (plasmoid formation: Hones et al. 1984) that can thus be modelled as a repeatable phenomenon which nonetheless has an apparently random spread of properties around a well-defined mean. Deterministic low-dimensional chaotic systems thus explain a broad distribution in inter-substorm waiting times without recourse to any stochasticity (Lewis 1991). This class of model points to only a few parameters being necessary to determine the state of the system. Sharma (1995) considered a data-driven approach to systemizing the substorm cycle as a low-dimensional system. Sharma et al. (1993) used Singular Spectrum Analysis (SSA) to project the time-series of driving and dissipation (solar wind input parameters and geomagnetic indices) to construct the low-dimensional dynamical space in which the system moves. By truncating to the first few components this space becomes low-dimensional (few degrees of freedom) and the system orbits on a manifold in this space that is folded- so that there is a catastrophe or discontinuous jump. Again, the motion is deterministic but can exhibit a broad distribution of waiting times and event sizes. All approaches in this class require the system to be low-dimensional, and as observations became more extensive it became clear that important physics is occurring across a broad range of spatio-temporal scales. How these approaches could be extended to understand the substorm-storm relationship is an open question. The system also can relax in principle via steady reconnection, and has a strong-driving limit. These driving and relaxation modes are naturally accommodated by the “dripping faucet” analogy.
3.3 High Dimensional and Stochastic
Following from new ideas in complexity science, there has been considerable interest in models that are intrinsically stochastic and high dimensional. The “poster child” for this kind of system is the avalanche, or “sandpile” model (Bak et al. 1987, 1988), intended to demonstrate Self Organized Criticality – SOC (reviews: Jensen 1998; Watkins et al. 2015) although there are a variety of interesting and potentially relevant models (Sornette 2006). The key elements that these models seek to capture are as follows. The system is high dimensional or has many degrees of freedom, that is, the physics enabling energy release and transport is occurring on multiple spatial and temporal scales. These processes are non-linearly coupled across a broad range of spatial and temporal scales. This is in contrast to systems which we can isolate to a specific space and timescale, such as an oscillator or wave, or indeed, a broad spectrum of waves which are not coupled and simply linearly propagate through each other. There is a separation of timescales, the driving of the system occurs slowly and dissipation and energy release (i.e., substorm onset and evolution) is fast. The system evolves through many metastable states, there is no single path to instability (substorm onset), it is a dynamical steady-state, not an equilibrium. The stochasticity in the system is intrinsic to the many paths through which the system can evolve. This class of model naturally codifies the idea of “multiscale” or “cross-scale” processes and indeed, the early work on sandpile models promoted this way of thinking about magnetospheric dynamics. Sandpile models were considered as having points of contact with auroral observation and magnetotail dynamics (Chapman et al. 1998; Lui et al. 2000; Uritsky and Pudovkin 1998; Consolini 1997; Uritsky et al. 2002) but it is important to differentiate between models as a way to illustrate and codify the important physics – simple sandpile models – in the same sense as Baker’s “dripping faucet” did for low-dimensional chaos, as opposed to detailed models that attempt to synthesise avalanche models and MHD (e.g., Klimas et al. 2005). Furthermore, stochastic systems near criticality can under some circumstances be characterized by a small number of relevant parameters (Chang 1992) so that observations will exhibit low-dimensional behaviour as described above.
These approaches are perhaps most valuable in that they drove new ways of looking at the data. They predict that the onset time of the substorm will be inherently uncertain, whereas event sizes will be predictable in their statistical distribution. Importantly, these statistical models do not aim to reproduce specific detailed time-sequences of events that are seen in the data. They do not identify a specific instability or detailed scenario of evolution of the system with energy transport, indeed, under different conditions, the system will utilize different pathways for energy transport and release. This perspective suggests that a quantitative statistical approach to the data can capture relevant aspects of the system’s behaviour. Although the solar wind driving of the magnetosphere and its response are highly variable, their statistical distributions quantify space weather risk (Chapman et al. 2020 and references therein) and are found to have properties that are independent of variation across solar cycles (Hush et al. 2015; Tindale and Chapman 2016; Tindale et al. 2018; Chapman et al. 2018) supporting space weather prediction and providing a quantitative benchmark for space weather models.
Alongside these complexity-led approaches, there is a well-developed field of stochastic processes, that is, developing stochastic and kinetic equations (Langevin, Fokker-Planck and Fractional Kinetics) that capture the essential features of the stochastic timeseries. These have found application in describing solar wind parameters and geomagnetic indices (Hnat et al. 2004; Watkins et al. 2009a; Alberti et al. 2018) and the relationships between them (Hnat et al. 2005).
It is important to distinguish these approaches from the extensive work on turbulence where models and methods developed in the mainstream turbulence literature have found both application and development in quantifying the scaling properties of fluctuations in the solar wind, magnetosheath and magnetotail (see e.g., Borovsky 2021). Turbulence and SOC can be clearly distinguished in their limiting behaviour (Chapman et al. 2009) but are more challenging to distinguish observationally in the finite-sized systems that we find in solar and magnetospheric physics (e.g., Watkins et al. 2009b).
3.4 An Emergent Transition from Small to Large Scale Coherent Structure
Model driven approaches to the observations, such as those described above, when at their best frame the analysis in terms of testing a hypothesis – the data supports the model or it does not. Limitations of the data, and oversimplification in the models, can often mean that quite distinct physical pictures are corroborated by some aspect of the observations when viewed through a specific methodology. The methods used for quantifying low-dimensional deterministic dynamics, and high-dimensional stochastic behaviour, can be quite distinct and may only extract the properties consistent with one or the other. We are now moving from a data-poor to a data-rich era of space plasma physics. Hence there is new interest in data analysis methods that can handle large and diverse datasets and are, as far as possible, non-parametric and model independent.
Network science is a well-established and highly active field, it provides a system for extracting pattern from large datasets. Networks can be dynamic (i.e., time-evolving) and directed (codifying information flow). Once a network is formed from the data, it can be characterized by parameters that capture its topological properties (Dods et al. 2017). This quite recent approach has already found application in ionospheric total electron content – TEC (McGranaghan et al. 2017; Zou et al. 2011; Liu et al. 2020) and in ground-based magnetometers (Orr et al. 2019, 2021). Networks find natural application to non-uniform spatial sampling and can extract the pattern of spatial correlation without requiring any gridding of the data, desirable as gridding necessarily introduces its own spatial correlation. An important non-trivial consideration is that the data needs to be uniformly calibrated, as is the case of the SuperMAG network (Gjerloev 2012). Network characterization of spatio-temporal correlation is in principle model-independent. This is a major advantage, in that a single analysis based on networks can capture both high dimensional (many small interacting structures) and low-dimensional (few, large-scale coherent structures) behaviour. Naturally, the analysis is limited to the spatial and temporal resolution of the measurements. Thus, in the analysis of substorms (Orr et al. 2021), we can capture the transition from many, meso-scale (a few hundreds of km) current filaments around onset, to one single current wedge at expansion phase. This picture of a substorm is the emergence of large-scale structure which is always repeatable, from meso-scale structures which may differ from one event to another. Since all the physics (that can be resolved by the observations) is captured, one can test against competing hypotheses, most clearly, whether the substorm current wedge is a single large-scale coherent structure or many small wedge-type current systems as a result of individual flux bundles.
This approach can in principle be extended to three spatial dimensions and to combine different, inhomogeneous data, which will enable both the exploration of extensive datasets, and data-model comparison. Since it reduces the detailed multipoint observations to a few topological network parameters, it allows statistical inter-event comparison to determine to what extend the behaviour is repeatable, which features are typical and predictable and which are essentially unpredictable. It may ultimately lead to a synthesis of the ideas developed above, so that the system in fact at different times/phases of activity exhibits high, or low-dimensional behaviour. This kind of understanding is essential to understanding what about the system is predictable, and what will be straightforward, or highly challenging, to capture in advanced space weather modeling. An example of this analysis is shown in Fig. 5 and Fig. 6.
(adapted Fig. 2 from Orr et al. 2021) Evolution of network community structure at the onset of the 16 March 1997 storm as seen by SuperMAG. Polar plots are in magnetic coordinates centered at the magnetic pole, with midnight located at the bottom of each panel. (MLT = 0 h). Maps show the nightside from dusk (MLT = 18 h) to dawn (MLT = 6 h) and 60–90° magnetic latitude. Magnetic field perturbation vectors (North and East components, BN,E) are plotted in black. Polar VIS images are superimposed on each panel. Each panel (a–f) shows a snapshot of the community structure in intervals of five normalized minutes from before onset (a, \(t'=-5\)) to the time of maximum expansion (f, \(t'= 20\)). The circles represent ground magnetometer locations with the line representing the BN,E vector. Black magnetometers are not part of a community. Each individual community is indicated by a different colour. See Orr et al. (2021) for details, this study analysed 41 isolated substorms, and whilst the evolution towards onset is unique for each event, the final state is a single large-scale community, indicative of a single large-scale current wedge
(adapted Fig. 3 from Orr et al. 2021) The normalized modularity, QN, of a set of 41 substorms that have two or more magnetometers in four even local time sectors of the nightside and are quiet before onset. Panels a, b normalized time is the abscissa. Panel a ordinate indicates bins of QN at each normalized time and the color intensity indicates the probability as indicated by the colour bar on the rhs of the panel (count of substorms with QN/total number of substorms). Panel b plots QN of each of the 41 substorms as a function of normalized time, \(t'\), as thin light gray lines. The median is overplotted in black and the 25 and 75% quantiles in darker gray. Panel c plots the normalized histograms of QN of the events aggregated over 10-min intervals as time progresses. The median is overplotted on each histogram. See Orr et al. (2021) for details, whilst there is a wide variation in network modularity before onset, by 20 minutes after onset the modularity falls to a low value, indicating that the network is dominated by a single community
4 Contributions to Storm Research
At the beginning of the space age, Akasofu (1964), discovered and described a sequence of auroral brightenings and expansions in the midnight sector at auroral latitudes. These events occurred up to a half dozen times a day during relatively geomagnetic quiet intervals. Because there were no spacecraft carrying auroral cameras at the time, Akasofu made this discovery using multiple ground-based all sky camera photographs of auroras laid out on his living room floor. Sydney Chapman, the then PhD advisor of Akasofu, demanded that Akasofu call these events “substorms” in his publication on the topic (Akasofu, personal communication, 2016). To this day everyone agrees that a substorm is indeed the fundamental mode of massive energy deposition into the magnetosphere and ionosphere. However, concerning the exact triggering mechanism, there are many different ideas (magnetic reconnection: Dungey 1961; Russell and Elphic 1978; current driven instabilities: Huba et al. 1977; Coroniti and Eviatar 1977; ion tearing mode instability: Schindler 1975; Galeev et al. 1978; Zelenyi and Kuznetsova 1984; Lakhina and Tsurutani 1998; ballooning instability: Roux et al. 1991), all of them with strong arguments in favor of them. It is possible that all of these mechanisms are indeed correct in that there are several different causes of substorm macroinstabilities.
The part of the concept of a substorm which is still controversial today is its role with magnetic storms. Both Chapman and Akasofu considered a substorm to be an integral part of a magnetic storm, thus the name. The idea is that many substorms added together made up a magnetic storm. To discuss this further, we first need to describe what a magnetic storm is and isn’t.
In the 1960s, it was thought that magnetic storms had three main phases, the “initial phase” where the Dst index (Iyemori 1990) becomes and remains positive, the storm main phase where the Dst index becomes negative, and the recovery phase, where the Dst index recovers to its background (∼0 nT) level. From space age satellite observations, it was found that it was magnetic reconnection between the interplanetary magnetic field (IMF) and the Earth’s magnetopause magnetic field leads to solar wind energy input into the magnetosphere during magnetic storms (Rostoker and Fälthammar 1967; Gonzalez and Tsurutani 1987; Tsurutani et al. 1988; Zhang et al. 2007; Echer et al. 2008). The mechanism of magnetic reconnection and energy injection into the nightside region of the magnetosphere was proposed by Dungey (1961). The superthermal plasmasheet plasma is convected and adiabatically energized to ∼10 to 300 keV as it is injected into the magnetosphere to form the ring current. The particles form a ring of current through gradient and curvature drift, thus the name. The total amount of particle kinetic energy of the ring current particles is linearly related to the decrease in the Dst indices, indicating that Dst is a good quantitative measure of the storm intensity (Dessler and Parker 1959; Sckopke 1966).
This magnetic reconnection on both the dayside and nightside magnetosphere (Dungey 1961) and the formation of the enhanced ring current thus causes the main phase of the magnetic storm. What are the interplanetary parameters that are the causes of magnetic reconnection and magnetic storms? Well obviously southward magnetic fields for one and solar wind velocity for another. Combined together they are the interplanetary electric field \(\mathrm{E} = \mathrm{V} \times \mathrm{B}\). Also a factor, but less of one is the plasma density (Gonzalez et al. 1989). Echer et al. (2008) have shown that all 90 major magnetic storms with \(\mathrm{Dst} < -100\text{ nT}\) that occurred in solar cycle 23 were due to southward IMFs. Tsurutani and Gonzalez (1995) showed that with northward IMFs geomagnetic quiescence occurred. The energy input into the magnetosphere was 100 to 30 times less than during southward IMFs.
Then what is the “initial phase” and its physical cause? It was experimentally found by Smith (1979) and Tsurutani et al. (1988) that magnetic storms generated near solar maximum were typically caused by Interplanetary Coronal Mass Ejections (ICMEs) and their upstream sheaths. ICMEs are the interplanetary remains and evolution of CMEs coming from the Sun. The fast CMEs are led (on the antisunward side) by fast mode collisionless shocks (Kennel et al. 1985), which have compressed and accelerated the slow solar wind forming the sheaths. The abrupt plasma density jump at the shock/sheath causes a sudden compression of the Earth’s magnetosphere due to the increase in the solar wind ram pressure. This compression is noted as a “sudden impulse” (SI+) by ground-based magnetometers (Araki et al. 2009). However, if there is no southward IMF component in the sheath or following ICME proper, there is no enhanced magnetic reconnection and thus no magnetic storm main phase. For this reason, modern scientists have dropped the term storm “initial phase” because it is just magnetospheric compression and not part of the storm itself. This has been discussed in detail by Joselyn and Tsurutani (1990) in which they suggest that the term “Storm Sudden Commencement” (SSC) be dropped from the literature. The shock will always produce a “sudden impulse” (Araki et al. 2009) and that term should be used instead.
The magnetic recovery phase is caused by the loss of the energetic ring current particles. This has been described and modeled by Kozyra et al. (1997, 2002) and Jordanova et al. (1998). The loss processes are charge exchange, Coulomb collisions, wave-particle interactions (with consequential particle loss to the ionosphere) and convection out the dayside magnetopause.
When Chapman and Akasofu coined the term “substorm”, they realized that although substorms occur during all phases of magnetic storms, there were far more events during the storm main phase than either of the other two. This led to their speculation that substorms were the building blocks of magnetic storm main phases.
Is there observational evidence contrary to the Chapman and Akasofu hypothesis that magnetic storm (main phases) are caused by multiple substorms?
The answer is yes, on two different fronts. Tsurutani et al. (2004) searched for magnetic storms with a lack of substorms. The magnetic storms were identified by events where \(\mathrm{Dst} < -50\text{ nT}\) and substorms were identified by high values of the AE indices. They found that magnetic storms caused by slowly rotating southward interplanetary magnetic fields would create Dst depressions that would quantitatively qualify as magnetic storms. These slowly rotating magnetic fields were part of the magnetic cloud (MC) portion of the ICME. These storms had a significant lack of AE substorms or no substorms at all. So there are published examples of storms without substorms.
But is that the end of the argument? Well not quite. These events appeared as large amplitude “convection bays” (Pytte et al. 1978; Sergeev et al. 1996). The question then becomes “is this not a true magnetic storm, but some other geophysical phenomena?”. This topic has yet to be answered.
There is another form of geomagnetic activity besides isolated substorms and magnetic storms. This geomagnetic activity that occurs associated with Alfvén waves embedded in high speed solar wind streams. The streams emanate from coronal holes primarily during the declining phase of the solar cycle (Krieger et al. 1973; McComas et al. 2002). Earlier Tsurutani and Gonzalez (1987) found this activity and gave it a descriptive name, “High-Intensity Long-Duration Continuous AE Activity” (HILDCAA) event. These events had to occur outside of a magnetic storm, had to last 2 days or longer, reached peak AE values of 1000 nT or higher, and had no lapse of AE less than 200 nT for 2 hours or more. The southward component of the Alfvén waves caused magnetic reconnection and the consequential HILDCAA geomagnetic activity. HILDCAAs have been found to be a series of substorms (identified by spacecraft imaging), but there are other “convection events” present as well (Tsurutani and Gonzalez 2007). The convection events are now recognized as being associated with Nishida (1968) DP2 current systems. However, the main point is that HILDCAAs are an example of many consecutive substorms/convection events that do not form a magnetic storm. Thus, this is a contrary example from another perspective.
If magnetic storms are different from a series of substorms what is the relationship between the two?
We know from observations that both are caused by southward interplanetary magnetic fields and magnetic reconnection. Substorms occur from short duration southward fields (Tsurutani and Meng 1972; Kamide et al. 1977). Magnetic storms are caused by long duration and intense southward magnetic fields (Gonzalez et al. 1994; Daglis et al. 2007). During most (main phase) magnetic storms there are many substorms as well.
It is possible that the two phenomena are independent and the two systems can be operational at the same time (Tsurutani and Gonzalez 2007). Magnetic storms involve large scale entire magnetospheric convection patterns. The convection electric fields produce the energization for the ring current formation. Substorm reconnection and subsequent convection is more highly localized and involve only a relatively small portion of the nightside magnetosphere. One test to determine if this scenario is correct and the two systems can operate at the same time is to study nightside electric fields and determine if two separate systems are coexisting.
When we mention that magnetic reconnection is the cause of storms and substorms, it is clear that there are other interplanetary parameters that influence the efficiency of the magnetic reconnection process (Gonzalez et al. 1989; Borovsky 2013). It is also known that interplanetary shock impingement onto the magnetosphere can trigger substorms (Heppner 1955; Zhou and Tsurutani 2001). In some cases, the substorms are so intense that they may be the main energy input factor for a coincident magnetic storm (Tsurutani and Hajra 2021; Hajra et al. 2016; Hajra and Tsurutani 2018). What is the source of this substorm/storm energy? There is probably stored magnetotail energy but additional solar wind ram kinetic energy cannot be ruled out as well.
Application of Information-Theoretic Measures for Storm Research
Information-Theory measures, such as the ones discussed in Sect. 2.4, can provide valuable insights into the state of the magnetosphere and the various changes that it is subjected to, and thus, can be used to study and characterize the onset and evolution of phenomena such as magnetic storms. In Balasis et al. (2013) the authors have used various entropies to study the variations in the information content of the Dst series, for the entire year of 2001, which included two intense magnetic storms, on March 31st and November 6th, with values that reached a minimum of \(-387\text{ nT}\) and \(-292\text{ nT}\) respectively. They used the Tsallis entropy formula, with a q value equal to 1.84, on the binary representation of the series, as well as the Approximate, Sample and Fuzzy entropies, the latter of which with an exponential membership function.
As can be seen in Fig. 7, all measures accurately detect the complexity dissimilarity among different “physiological” (quiet times) and “pathological” (intense magnetic storms) states of the magnetosphere. They imply the emergence of two distinct patterns: a pattern associated with the intense magnetic storms, which is characterized by a higher degree of organization (lower entropy values) and a pattern associated with normal periods, which is characterized by a lower degree of organization (higher entropy). In general, all four entropy measures clearly distinguish between the different complexity regimes in the Dst time series.
(Fig. 1 from Balasis et al. 2013) From top to bottom: Dst time series from January 1, 2001, to December 31, 2001, associated with two intense magnetic storms (marked in red) and the corresponding ApEn, SampEn, FuzzyEn and non-extensive Tsallis entropy, \(S_{q}\), for sliding windows of 256 hours each. The triangles denote five time intervals in which the first, third and fifth intervals correspond to higher entropies, whereas the second and fourth time windows exhibit lower entropies (the parts of the entropy plots shown in red)
5 Solar Wind Driving of Radiation Belt Dynamics
Characterizing and modeling processes at the sun and of space plasma in our solar system are difficult because the underlying physics is often complex, nonlinear, and not well understood. The drivers of a system are often nonlinearly correlated with one another, which makes it a challenge to understand the relative effects caused by each driver. However, entropy-based information theory can be a valuable tool that can be used to determine the information flow among various parameters, causalities, untangle the drivers, and provide observational constraints that can help guide the development of theories and physics-based models. Similarly correlative methods provide a basis for ranking solar wind functions in terms of their geoeffectiveness, and for building models driven by these solar functions. The solar wind drivers of radiation belt electrons are investigated using correlation functions, mutual information (MI), conditional mutual information (CMI), transfer entropy (TE), and impulse response functions (IRF). Relativistic electron fluxes at the geosynchronous orbit (herein \(J_{ e, \mathrm{GEO}}\) refers to geosynchronous MeV electron energy flux) is found to be anticorrelated with solar wind density (\(n_{\mathrm{sw}}\)) with a lag of 1 day. However, this lag time and anticorrelation can be attributed mainly to the \(J_{e,\mathrm{GEO}}(t + \text{2 days})\) correlation with solar wind velocity, \(V_{\mathrm{sw}}(t)\), and the anticorrelation of solar wind density and velocity over timescale of 1 day. Analyses of solar wind driving of the magnetosphere need to consider this \((V_{\mathrm{sw}}, n_{\mathrm{sw}})\) anticorrelation. Using CMI to remove the effects of \(V_{\mathrm{sw}}\), the response of \(J_{e,\mathrm{GEO}}\) to \(n_{\mathrm{sw}}\) is 30% smaller and has a lag time <24 hr, suggesting that the loss mechanism due to \(n_{\mathrm{sw}}\) or solar wind dynamic pressure has to start operating in <24 hr. Nonstationarity in the system dynamics is investigated using windowed TE. The solar wind drivers are then investigated using filtering methods: the impulse response functions of the electron flux, as a function of L shell and energy, to solar wind velocity, density, and interplanetary magnetic field are presented. We discuss the physical significance of three large-scale modes in these responses. Determining the spatial, temporal, and energy parameters of these modes narrows down the search for the salient acceleration and loss processes in the radiation belts. Finally, we present linear and nonlinear dynamical models of the electron flux.
5.1 Introduction
The Earth’s radiation belts refer to a region in space that is populated by trapped energetic electrons and ions. Typically, there are two electron radiation belts, the inner belt and outer belt, but sometimes a third belt appears between the two belts. The inner belt is located at an equatorial distance approximately between 1.2 and 3 \(\mathrm{R}_{\mathrm{E}}\) (\(\mathrm{R}_{\mathrm{E}}\) = radius of the Earth ∼6378 km) from the center of the Earth and contains electrons having energies of hundreds of keVs and ions having hundreds of MeVs. The outer belt is located at an equatorial distance approximately between 4 and 8 \(\mathrm{R}_{\mathrm{E}}\) and contains mostly electrons having energies ranging from a few hundred keVs to tens of MeVs. The present chapter deals only with the outer radiation belt electron population.
The existence of radiation belt MeV electrons is usually explained by several acceleration mechanisms that can accelerate electrons from a few keVs to tens of MeVs.
There have been several acceleration mechanisms proposed, but most studies generally suggest either local or global acceleration. In a local acceleration scenario, storms and substorms inject plasma-sheet particles into the inner-magnetosphere and accelerate low-energy (e.g., few-keV) electrons to a few hundred keVs. Once in the inner magnetosphere, electrons interact with locally excited ultra-low-frequency (ULF) waves (e.g., Elkington et al. 1999; Rostoker et al. 1998; Ukhorskiy et al. 2005; Mathie and Mann 2000, 2001), very-low-frequency (VLF) waves (e.g., Summers et al. 1998; Omura et al. 2007; Thorne 2010; Simms et al. 2015; Camporeale 2015; Camporeale and Zimbardo 2015), and/or magnetosonic waves (e.g., Horne et al. 2007; Shprits et al. 2008), which can energize electrons to the MeV-energy range. The solar wind velocity may be linked to the local acceleration mechanism through substorm particle injections (e.g., Baker and Kanekal 2008; Kissinger et al. 2011; Tanskanen 2009; Kellerman and Shprits 2012; Newell et al. 2016).
Although the previous paragraph would link the substorm injections and electron acceleration to high \(V_{\mathrm{sw}}\), some studies emphasized the role of the southward component of the magnetic field, especially during high-amplitude Alfvén waves, and High Intesity Long Duration Continuous AE Activity (HILDCAA) events (Hajra et al. 2013). Tsurutani et al. (2010 and references therein) suggested that the process starts at the Sun with nonlinear Alfvén waves carried by high-speed solar wind streams emanating from coronal holes. The southward component of the Alfvén wave magnetic field would cause magnetic reconnection at the dayside magnetopause, which would lead to energetic plasma injections on the nightside and electron acceleration (this is discussed further in the Journal of Geophysical Research (JGR) Special Section on Chorus, Tsurutani et al. (2010)).
Certain global-acceleration mechanisms also invoke ULF waves for electron acceleration. A popular scenario is that the ULF waves are generated globally by a Kelvin-Helmholtz instability (KHI) along the magnetopause flanks due to large velocity shear between the magnetosheath and magnetosphere plasmas (e.g., Johnson et al. 2014; Engebretson et al. 1998; Vennerstrøm 1999). Indeed, studies have shown that \(V_{\mathrm{sw}}\) is probably the most dominant driver of relativistic electron fluxes at geosynchronous orbit (6.6 \(\mathrm{R}_{\mathrm{E}}\)) (e.g., Paulikas and Blake 1979; Baker et al. 1990b; Li et al. 2001, 2005; Vassiliadis et al. 2005; Ukhorskiy et al. 2004; Rigler et al. 2007; Kellerman and Shprits 2012; Reeves et al. 2011; Hajra et al. 2015).
In contrast to \(V_{\mathrm{sw}}\), which correlates with \(J_{e,\mathrm{GEO}}\), \(n_{\mathrm{sw}}\) appears to anticorrelate with \(J_{e,\mathrm{GEO}}\) (e.g., Lyatsky and Khazanov 2008; Kellerman and Shprits 2012); however, we are providing an explanation of this in Sect. 5.6 below. One mechanism supporting this anticorrelation states that an increase in \(n_{\mathrm{sw}}\) would increase solar wind dynamic pressure (\(P_{\mathrm{dyn}}\)), which, in turn, would push the magnetopause inward, leading to electron losses at the high L shell (e.g., Li et al. 2001). Furthermore, the magnetopause compression would drive ULF waves (e.g., Korotova and Sibeck 1995; Kepko and Spence 2003; Claudepierre et al. 2010) leading to fast radial diffusion, which redistributes the losses to lower L shells, including at geosynchronous orbit (Shprits et al. 2006; Kellerman and Shprits 2012; Turner et al. 2012). Ukhorskiy et al. (2006) used a test particle simulation to demonstrate this scenario, which is known as magnetopause shadowing (West et al. 1972). However, there is evidence that solar wind density can lead to electron acceleration at L < 4 (Vassiliadis et al. 2003, 2008, 2011).
Information theory has been applied to problems in magnetospheric, ionospheric, and solar physics (e.g., Consolini et al. 2009; Balasis et al. 2011a; Materassi et al. 2011; De Michelis et al. 2011, 2017b; March et al. 2005; Johnson and Wing 2005; Johnson et al. 2018; Johnson and Wing 2014; Wing et al. 2005, 2016, 2018, 2022). We will use some of its tools in later parts of this section.
Returning to the question of whether the density leads to energization or losses, we note that, in the solar wind, \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) are anti-correlated with each other (e.g., Hundhausen et al. 1970) while pressure balance is maintained. The anti-correlation of \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) complicates the interpretation of the driving of the \(J_{e,\mathrm{GEO}}\). If \(V_{\mathrm{sw}}\) is causally correlated with \(J_{e,\mathrm{GEO}}\), the anticorrelation between \(J_{e,\mathrm{GEO}}\) and \(n_{\mathrm{sw}}\) could simply be coincidence. Conversely, if \(n_{\mathrm{sw}}\) is causally correlated with \(J_{e,\mathrm{GEO}}\), the anticorrelation between \(V_{\mathrm{sw}}\) and \(J_{e,\mathrm{GEO}}\) could simply be coincidence. On the other hand, we cannot rule out the possibility that both \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) can produce effects on the electron flux. If that is the case, how can we untangle the effects of \(V_{\mathrm{sw}}\) from \(n_{\mathrm{sw}}\) and which of these two parameters exert more influence on \(J_{e,\mathrm{GEO}}\)?
In the following, we review our recent work applying information theory to solar wind–radiation belt system. We demonstrate how information theory can be used to untangle the solar wind drivers of the radiation belt. The information theoretic tools that we use are mutual information (e.g., Li 1990; Tsonis 2001), conditional mutual information (e.g., Wyner 1978), and transfer entropy (e.g., Schreiber 2000).
5.2 Data Sets
Electron Flux at Geosynchronous Orbit
The geosynchronous orbit is a useful location for measuring the electron flux, \(J_{e,\mathrm{GEO}}\). The solar wind–radiation belt system study uses daily averages of MeV electron fluxes obtained from Energetic Sensor for Particles (ESP) (Meier et al. 1996) and Synchronous Orbit Particle Analyzer (SOPA) (Belian et al. 1992) on board of all seven Los Alamos National Laboratory (LANL) geosynchronous satellites from 22 September 1989 to 31 December 2009. The data and format description can be found at ftp://ftop.agu.org/apend/ja/2010ja015735. We only examine the \(J_{e,\mathrm{GEO}}\) flux of electrons with energy range of 1.8–3.5 MeVs. A detailed description of the dataset and its processing are given in Reeves et al. (2011).
Electron Flux at Other Altitudes in the Radiation Belts
The electron flux is a function of electron position and velocity, denoted by \(J_{{e}}(t; \mathrm{L}, \mathrm{E}, \alpha )\) where the last three arguments are L shell, energy, and pitch angle. In practice we will use the logarithmic flux (also: log-flux), \(j_{e} =\log J_{e}\).
In addition to measurements of the flux from geosynchronous orbit (corresponding to a narrow range of L shells), it is possible to measure the flux from other orbits, some of which go through the high-activity regions in the belts. Therefore, we discuss spacecraft missions such as the Solar Anomalous and Magnetospheric Particle Explorer (SAMPEX), the Polar spacecraft in NASA’s Global Geospace Science program, and the recent Van Allen Probes (VAP) which have proven invaluable in the understanding of the dynamics and physics of the belts.
SAMPEX (1992-2012) traveled in a polar, roughly circular, low-Earth orbit (LEO) with a 96.7-min period which provided high-cadence measurements over the entire L shell range of the radiation belts (the resolution in L used below is \(\Delta \mathrm{L} = 0.1\)). Limitations included a) the spacecraft’s low altitude which allowed measurements of only part of the particle distribution near the loss cone – which, however, proved sufficiently representative of the large-scale changes of the full distribution; b) a very sparse energy sampling (relevant to this discussion: the 2-MeV channel of the Proton Electron Telescope, or PET), and c) occasional contamination of the detector by protons. SAMPEX, however, has been a valuable mission for its energy coverage as well as its longevity and reliability. In the following we discuss analysis of several years of daily-averaged electron flux data measured by PET. Figure 8 shows representative orbits of SAMPEX and other spacecraft.
(Fig. 1 from Vassiliadis 2008) SAMPEX and Polar missions: representative orbits
Polar was in a highly elliptical (apogee: 9 RE), high-inclination (78.63°) orbit. Its long period of 18.5 hours was compensated to a certain extent by its excellent instrumentation. The Comprehensive Energetic Particle and Pitch Angle Distribution (CEPPAD) detector provided 3-D electron angular distributions in the energy range of 20 keV-1 MeV. We will mention the analysis of electron flux data from the HIST sensor of CEPPAD from a three-year interval (1997-1999) at the beginning of the mission at a daily resolution.
The VAP mission was active from August 2012 to October 2019. This study uses data from the VAP-A spacecraft which has a highly elliptical, low-inclination (10.2°) orbit and goes rapidly through a wide L shell range with a period of 8.95 hours. Because the particle counts drop off rapidly at high L shells, the shell range for this study is \(\mathrm{L}^{*} = 1.1\text{-}6.5\); in addition, we use a resolution of \(\Delta \mathrm{L}^{*} = 0.1\). The Energetic-Particle, Composition, and Thermal-Plasma (ECT)’s Magnetic Electron and Ion Spectrometer (MagEIS) measures electrons with 25 channels in the range 31.5 keV-4.22 MeV and a large number of pitch angle channels. Here we will present results for the omnidirectional electron flux dataset from one year (2015) at a 6-hour resolution. The analysis was originally done with Release 3 data (Vassiliadis 2018) and repeated with virtually identical results with Release 4 data (Vassiliadis 2019); only the latter results are discussed below.
Interplanetary and Magnetospheric Activity
To properly understand the dynamics of the radiation belt electron flux, we must place it in the context of interplanetary and broader magnetospheric activity. For the studies of electron flux at geosynchronous orbit (LANL spacecraft data), the daily and hourly averaged solar wind data 1989–2009 come from OMNI dataset provided by NASA (http://omniweb.gsfc.nasa.gov/). The LANL and solar wind data are merged. The LANL electron flux dataset has 7187 daily averages out of which 6438 data points have simultaneous solar wind observations.
A similar approach is applied to studies of electron flux from off-geosynchronous orbits. Solar wind, IMF, and solar measurements are obtained from NASA’s OMNIweb service and are interpolated and/or averaged to be in the same time resolution as those of the magnetospheric particle fluxes. The timescales range from 1 day (SAMPEX and Polar) to 6 hours (VAP).
Radiation belt events are part of the overall magnetospheric activity. As such it is correlated with geomagnetic indices (Dst, AL, AU, PC) which are regional or global measures of magnetospheric activity.
5.3 Radiation Belt Structure in Configuration Space and Energy Space
As discussed in the Introduction to this Section, the motion of electrons in the radiation belts is determined by a large number of magnetospheric and interplanetary effects. As a result the dynamics of phase space density \(f(\mathbf{x}, \mathbf{v}, t)\) and the flux \(j_{{e}}(\mathbf{x}, \mathrm{E}, \alpha , t)\) in one region of the inner magnetosphere can significantly differ from their dynamics in another region.
We can use the dynamics of the measured electron flux to discern these regions in configuration space or energy space. For simplicity we use omnidirectional fluxes \(j_{\mathrm{e}}(t; \mathrm{L}, \mathrm{E})\) and average over either the energy or the L shell. Our starting point is the cross-correlation function for time series \(x(t)\) and \(y(t)\) defined in Equation (2.9) which we will apply to the energetic electron fluxes at specific L shells and energies.
First, we compare energy-averaged fluxes \(j_{{e}}(\mathrm{L}_{1}, t)\) and \(j_{{e}}(\mathrm{L}_{2}, t)\) at shells \(\mathrm{L}_{1}\) and \(\mathrm{L}_{2}\), measured over time intervals \(T\) long compared to drift periods, e.g., many days and typically a year or longer. The L-shell correlation
is a measure of the spatial coherence of the radiation belt regions (Vassiliadis et al. 2003). For 2-MeV omnidirectional fluxes measured by SAMPEX/PET at a daily time resolution from 1993-2000, we obtain a correlation matrix (Fig. 9) (Vassiliadis et al. 2003). The correlation matrix is divided into symmetric off-diagonal blocks (diagonal correlations are trivially unity). We identify several spatial regions with correlated dynamics: a) the main outer belt (L = 4-7); b) the inner edge of outer belt (L = 3-4); c) the slot (L = 2-3); and d) the inner belt (L = 1.1-2). The L shell ranges obtained from the correlation function indicate that different processes predominate in each region and determine its dynamics.
(adapted Fig. 2 from Vassiliadis et al. 2003) Cross-L correlations from 2-MeV daily omnidirectional fluxes measured by SAMPEX/PET over the range L = 1.1-10.0 in the interval 1993-2000
Second, we compare L shell-averaged fluxes \(j_{{e}}(t; \mathrm{E}_{1})\) and \(j_{{e}}(t; \mathrm{E}_{2})\) at energies \(\mathrm{E}_{1}\) and \(\mathrm{E}_{2}\), measured over long time intervals \(T\). We define the energy correlation
as a measure of the coherence in energy space (Vassiliadis 2018). For omnidirectional fluxes measured by VAP-A/MagEIS at a 6-hour resolution over 1 year (2015), we obtain a correlation matrix in the energy range 31.5 keV-4.22 MeV (Fig. 10).
Cross-energy correlations from 6-hour omnidirectional fluxes measured by VAP-A/MagEIS over the range 31.5 keV-4.22 MeV in 2015 (Vassiliadis 2018)
The correlation matrix is divided into blocks which identify three distinct energy regions:
-
1.
31.5-143 keV. This range includes seed electrons and the low end of the acceleration range.
-
2.
184-749 keV. This range includes the intermediate acceleration.
-
3.
909 keV-4.06 MeV. This range includes relativistic electrons.
The division of the correlation matrix indicates that the dynamics of the flux at each energy may be correlated with one or more other energy levels. The acceleration/loss processes determining the time series of the flux at each energy appear to be different at each one of the three ranges.
5.4 Electron Flux Dynamics at Geosynchronous Orbit
Correlation with Solar Wind Activity
Early observations showed a consistent correlation between electron flux at geosynchronous orbit and several measures of activity in the interplanetary medium.
Paulikas and Blake (1979) showed that the solar wind speed has the greatest correlation with the flux of relativistic electrons over a range of energies (0.14-3.9 MeV) measured by the geostationary ATS-1, −5, and −6 satellites. Those results were the basis for many other studies of the relation between electron fluxes and interplanetary activity. One can form the correlation function between the log-flux and a measure of interplanetary activity such as the solar wind speed:
At geosynchronous orbit, the correlation with solar wind speed peaks at 2 days after solar wind arrival, but this may be different for lower L shells.
Mutual Information, Conditional Mutual Information, and Transfer Entropy
Dependency is commonly used to understand how systems operate. The standard tool used to identify dependency is cross-correlation such as the ones above. Considering two variables, \(x\) and \(y\), the correlation analysis essentially tries to fit the data to a 2D Gaussian cloud, where the nature of the correlation is determined by the slope and the strength of correlation is determined by the width of the cloud perpendicular to the slope. The correlation analyses are useful, fast, and simple. However, they cannot describe nonlinear relationships and usually cannot be used to establish causalities.
The entropy-based information theory can help identify nonlinearities in the system, information transfer between input and output parameters, and the response times (lags). This nonparametric, statistics-based method is not constrained by the assumption of an underlying dynamics – rather the underlying (physics-based) dynamics is discovered by the approach and then ultimately utilized to improve predictions. Moreover, it can help untangle the input parameters that are correlated or anti-correlated with each other. It can also help modelers select input parameters and determine prediction horizon. The latter refers to how far ahead can one predict a variable. Hence, it can be a useful tool to study many complex systems. This approach should be considered complimentary to correlational analyses and to physics-based and empirical modeling efforts.
Mutual information (MI) (Tsonis 2001; Li 1990; Darbellay and Vajda 1999) between two variables, \(x\) and \(y\), compares the uncertainty of measuring variables jointly with the uncertainty of measuring the two variables independently. The uncertainty can be measured by any entropic measure; below we show this using the Shannon entropy. In order to estimate the entropies, it is necessary to obtain the probability distribution functions, which in this study are obtained from histograms of the data based on discretization of the variables (i.e., bins).
Suppose that two variables, \(x\) and \(y\), are binned so that they take on discrete values, \(\hat{x}\) and \(\hat{y}\), where
The variables may be thought of as letters in alphabets \(\aleph _{1}\) and \(\aleph _{2}\), which have n and m letters, respectively. The extracted data can be considered as sequences of letters. The entropy associated with each of the variables is defined as
where \(p ( \hat{x}, \hat{y} ) \) is the probability of finding the letter \(\hat{x}\) in the set of \(x\)-data and \(p\)(\(\hat{y}\)) is the probability of finding letter \(\hat{y}\) in the set of \(y\)-data. To examine the relationship between the variables, we extract the letter combinations \(( \hat{x}, \hat{y} ) \) from the dataset. The joint entropy is defined by
where \(p ( \hat{x}, \hat{y} )\) is the probability of finding the letter combination \(( \hat{x}, \hat{y} )\) in the set of \((x, y)\) data.
The mutual information is then defined as
While MI is useful to identify nonlinear dependence between two variables, it is often useful to consider conditional dependency with respect to a conditioner variable \(z\) that takes on discrete values, \(\hat{Z} \in \{ \mathrm{z}_{1}, \mathrm{z}_{2},\ldots,\mathrm{z}_{\mathrm{n}}\} \equiv \aleph _{3}\). The conditional mutual information (Wyner 1978)
determines the mutual information between \(x\) and \(y\) given that \(z\) is known. In the case where \(z\) is unrelated, \(\operatorname{CMI}(x,y|z) = \operatorname{MI}(x,y)\), but in the case that \(x\) or \(y\) is known based on \(z\), then \(\operatorname{CMI}(x,y|z) = 0\). CMI therefore provides a way to determine how much additional information is known given another variable. CMI can be seen as a special case of the more general conditional redundancy that allows the variable \(z\) to be a vector (e.g., Prichard and Theiler 1995; Johnson and Wing 2014).
A common method to establish causal-relationships between two time series, e.g., [\(x_{t}\)] and [\(y_{t}\)], is to use a time-shifted correlation function in Equation (2.9). The results of this type of analysis may not be particularly clear when the correlation function has multiple peaks or there is not an obvious asymmetry. Additionally, correlational analysis only detects linear correlations. If the feedback involves nonlinear processes, its usefulness may be seriously limited.
Alternatively, time-shifted mutual information, \(\operatorname{MI}(x(t), y(t + \tau ))\), can be used to detect causality in nonlinear systems, but this too suffers from the same problems as time-shifted correlation when it has multiple peaks and long range correlations.
A better choice for studying causality is the one-sided transfer entropy (Schreiber 2000)
where \(yp_{t} = [ y_{t}, y_{t-\Delta},\ldots , y_{t-k\Delta} ]\), \(k + 1 = \text{dimensionality of the system}\), and \(\Delta = \text{first minimum in } \operatorname{MI}[y(t), y(t - \tau )]\). Transfer entropy (TE) can be considered as a specialized case of conditional mutual information:
where \(yp ( t ) = [ y ( t ),y ( t-\Delta ),\ldots ,y ( t-k\Delta ) ]\). The transfer entropy can be considered as a conditional mutual information that detects how much average information is contained in a variable \(x\) about the next state of variable \(y\) that is not contained in the past history of \(y\), \(yp\), of the system (Prokopenko et al. 2013). In the absence of information flow from \(x\) to \(y\), \(\operatorname{TE}(x \rightarrow y)\) vanishes. Also, unlike correlational analysis and mutual information, transfer entropy is directional, \(\operatorname{TE}(x \rightarrow y) \neq \operatorname{TE}(y \rightarrow x)\). The transfer entropy accounts for static internal correlations, which can be used to determine whether \(x\) and \(y\) are driven by a common driver or whether \(x\) drives \(y\) or \(y \) drives \(x\).
5.5 The Dilemma of the Solar Wind Drivers of the Radiation Belt System
Figure 11 plots the radiation belt \(j_{e,\mathrm{GEO}}\) vs. \(V_{\mathrm{sw}}\). The figure shows log \(j_{e,\mathrm{GEO}} (t + \tau )\) vs. \(V_{\mathrm{sw}}(t)\) for \(\tau = 0, 1, 2, \text{and }7\) days. The solar wind–radiation belt system is nonlinear and hence the standard linear correlational analysis would be inadequate. The radiation belt flux \(J_{{e}}\) is correlated with \(V_{\mathrm{sw}}\). The best correlation can be found with \(j_{e,\mathrm{GEO}}\) with a two-day lag, but it is hard to see this in the scatter plot in Fig. 11.
(Fig. 1 from Wing et al. 2016) Scatter plots of \(\log J_{e,\mathrm{GEO}}(t + \tau )\) vs. \(V_{\mathrm{sw}}(t)\) for \(\tau = 0, 1, 2, \text{and }7\) days in panels (a), (b), (c), and (d), respectively. The data points are overlain with density contours showing the nonlinear trends. The panels show that \(J_{e,\mathrm{GEO}}\) has dependence on \(V_{\mathrm{sw}}\) for \(\tau = 0, 1, \text{and } 2\) days and the dependence is strongest for \(\tau = 2\) days. (d) At large \(\tau \), e.g., \(\tau = 7\) day, \(J_{e,\mathrm{GEO}}\) dependence on \(V_{\mathrm{sw}}\) is very weak. The triangle distribution (Reeves et al. 2011) can be seen in panels (a), (b), and (c). This is essentially the same as Fig. 10 in Reeves et al. (2011), except that no density contours are drawn and Fig. 9d plots \(\tau = 7\) days instead of \(\tau = 3\) days
In order to see the best response lag time of the radiation belt \(j_{e,\mathrm{GEO}}\) to \(V_{\mathrm{sw}}\), Fig. 12 shows the plot of the \(\operatorname{corr}(j_{e,\mathrm{GEO}} (t + \tau ), V_{\mathrm{sw}}(t))\). The figure shows that the correlation coefficient peaks at \(\tau = 2\) day with \(r = 0.63\). There is a smaller peak at \(\tau = 29\) days (\(r = 0.42\)), which can be attributed to the 27 day synodic solar rotation. Because the large number of data points (\(n > 5772\)), the two peak correlation coefficients are highly significant with \(P < 0.01\). However, the linear correlational analysis may be inadequate because the solar wind–radiation belt system is nonlinear (Fig. 11). Hence, mutual information and transfer entropy need to be calculated. Figure 12b shows \(\operatorname{MI}(j_{e,\mathrm{GEO}} (t + \tau ), V_{\mathrm{sw}}(t))\) and \(\operatorname{TE}(V_{\mathrm{sw}} \rightarrow j_{e,\mathrm{GEO}})\). The figure shows that information transfer from \(V_{\mathrm{sw}}\) to \(j_{e,\mathrm{GEO}}\) peaks at \(\tau = 2\) days. Although in this case, the linear correlation, MI, and TE peak at the same \(\tau \), in general this is not always the case (as shown in the solar cycle analysis in Sect. 5.6).
(adapted from Wing et al. 2016) (a) Correlation coefficient of \([j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t)]\). (b) \(\operatorname{MI}(J_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t))\) (blue) and \(\operatorname{TE}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t))\) (yellow). The transfer of information from \(V_{\mathrm{sw}}\) to \(J_{e,\mathrm{GEO}} (\operatorname{TE}(V_{\mathrm{sw}} \tau j_{e,\mathrm{GEO}}))\) peaks at \(\tau _{\mathrm{max}} = 2\) days. (c) Correlation coefficient of \([j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t)]\). (d) \(\operatorname{MI}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t))\) (blue) and \(\operatorname{TE}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t))\) (yellow). The transfer of information from \(n_{\mathrm{sw}}\) to \(j_{e,\mathrm{GEO}} (\operatorname{TE}(n_{\mathrm{sw}} \tau j_{e,\mathrm{GEO}}))\) peaks at \(\tau _{\mathrm{max}} = 1\) day. (e) Correlation coefficient of \([n_{\mathrm{sw}}(t + \tau ), V_{\mathrm{sw}}(t)]\). (f) \(\operatorname{MI}(n_{\mathrm{sw}}(t + \tau ), V_{\mathrm{sw}}(t))\) (blue) and \(\operatorname{TE}(n_{\mathrm{sw}}(t + \tau ), V_{\mathrm{sw}}(t))\) (yellow). The solid and dashed green curves are the mean and \(3\tau \) from the mean of the noise. The transfer of information from \(V_{\mathrm{sw}}\) to \(n_{\mathrm{sw}} [\operatorname{TE}(V_{\mathrm{sw}} \tau n_{\mathrm{sw}})]\) peaks at \(\tau _{\mathrm{max}} = 1\) day
In order to get a measure of the significance of \(\operatorname{TE}(V_{\mathrm{sw}} \rightarrow j_{e,\mathrm{GEO}})\), we calculate noise = \(\operatorname{TE}(\operatorname{sur}(V_{\mathrm{sw}}) \rightarrow j_{e,\mathrm{GEO}})\) where \(\operatorname{sur}(V_{\mathrm{sw}})\) is the surrogate data of \(V_{\mathrm{sw}}\), which is obtained by randomly permuting the order of the time series array \(V_{\mathrm{sw}}\). The mean and standard deviation of the noise are calculated from an ensemble of 100 random permutations of \(\operatorname{TE}(\operatorname{sur}(V_{\mathrm{sw}}) \rightarrow j_{e,\mathrm{GEO}})\). The mean noise and \(3\sigma \) (standard deviation) from the mean noise are plotted with solid and dashed green curves, respectively, in Fig. 12b. The maximum TE, \(\operatorname{TE}(j_{e,\mathrm{GEO}} (t + \text{2 days}), V_{\mathrm{sw}}(t))\) has peak information transfer \(\mathit{it}_{\mathrm{max}} = 0.30\), signal to noise ratio \(\mathit{snr} = 5.7\) and significance = \(94\sigma \) where \(\mathit{it}_{\mathrm{max}} = \text{peak} - \text{mean noise}\), snr = peak/mean noise and significance = \(\mathit{it}_{\mathrm{max}}/\sigma \)(noise). From the snr, \(\mathit{it}_{\mathrm{max}}\), and significance, we conclude that there is a significant transfer of information from \(V_{\mathrm{sw}}\) to \(j_{e,\mathrm{GEO}}\) with a 2 day delay. Note that the linear correlation, MI, and TE analyses are consistent with the previous studies (e.g., Baker et al. 1990b; Vassiliadis et al. 2005; Reeves et al. 2011; Balikhin et al. 2011; Lyatsky and Khazanov 2008).
Figure 12c shows that the anticorrelation between \(n_{\mathrm{sw}}\) and \(j_{e,\mathrm{GEO}}\) minimizes at \(\tau = 1\) day (\(r = -0.49\)). Figure 12d shows that \(\operatorname{MI}(j_{e,\mathrm{GEO}} (t + \tau ), n_{\mathrm{sw}}(t))\) and \(\operatorname{TE}(n_{\mathrm{sw}}\rightarrow j_{e,\mathrm{GEO}})\) peak also at \(\tau = 1\) day (\(\mathit{it}_{\mathrm{max}} = 0.13\), \(\mathit{snr} = 4.4\) and significance = \(42\sigma \)). This result is consistent with Balikhin et al. (2011), which finds that \(J_{e}\) has the strongest dependence on \(n_{\mathrm{sw}}\) with a lag of 1 day.
However, \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) anti-correlate with each other (e.g., Hundhausen et al. 1970). Figure 12e shows that the anticorrelation between \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) minimizes at \(\tau = 1\) day (\(r = -0.56\)). Figure 12f shows that \(\operatorname{MI}(n_{\mathrm{sw}}(t + \tau ), V_{\mathrm{sw}}(t))\) and \(\operatorname{TE}(V_{\mathrm{sw}} \rightarrow n_{\mathrm{sw}})\) peak also at \(\tau = 1\) day (\(\mathit{it}_{\mathrm{max}} = 0.20\), \(\mathit{snr} = 7.4 \) and significance = \(95\sigma \)).
As mentioned in Sect. 5.1, the anti-correlation of \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) with a lag of 1 day complicates the interpretation of the driving of the \(j_{e,\mathrm{GEO}}\). If \(V_{\mathrm{sw}}\) is causally correlated with \(j_{e,\mathrm{GEO}}\) with a lag of 2 days, the anticorrelation between \(j_{e,\mathrm{GEO}}\) and \(n_{\mathrm{sw}}\) with a lag of 1 day could simply just be coincidence. Conversely, if \(n_{\mathrm{sw}}\) is causally correlated with \(j_{e,\mathrm{GEO}}\) with a lag of 1 day, the anticorrelation between \(V_{\mathrm{sw}}\) and \(j_{e,\mathrm{GEO}}\) could simply just be coincidence. On the other hand, from Fig. 12, we cannot rule out the possibility that both \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) can exert influence on the \(j_{e,\mathrm{GEO}}\). If that is the case, how can we untangle the effects of \(V_{\mathrm{sw}}\) from \(n_{\mathrm{sw}}\) and which of these two parameters exert more influence on \(j_{e,\mathrm{GEO}}\)?
5.6 Untangling the Drivers of the Radiation Belt Electron Flux
Geosynchronous Orbit
The correlation functions (Equation (2.9)) for a single input or even for multiple inputs are limited because a) they are linear, b) if there are multiple inputs, they are not always independent from each other. Therefore, and in an attempt to address the above question at the end of Sect. 5.5, we use conditional mutual information, CMI, to untangle the effects of \(V_{\mathrm{sw}}\) from \(n_{\mathrm{sw}}\) and vice versa. To calculate how much information flows from \(n_{\mathrm{sw}}\) to \(J_{e}\), given \(V_{\mathrm{sw}}\), we calculate \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t) | V_{\mathrm{sw}}(t))\), which is plotted as blue curve in Fig. 13a. Using a similar approach as for TE, we determine the noise level of the surrogates: \(\operatorname{CMI}(j_{e,\mathrm{GEO}} (t + \tau ), \operatorname{sur}(n_{\mathrm{sw}}(t)) | V_{\mathrm{sw}}(t))\). The mean and \(\sigma \) of the noise are calculated in the same manner as TE and used to determine the significance of the results. The mean noise and \(3\sigma \) are plotted as solid and dashed green curves respectively. Figure 13a shows that \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t) | V_{\mathrm{sw}}(t))\) peaks at \(\tau _{\mathrm{max}} = 0\) day with \(\mathit{it}_{\mathrm{max}} = 0.091\) and \(\mathit{snr} = 3.2\). The \(\tau _{\mathrm{max}} = 0\) day suggests that \(j_{e,\mathrm{GEO}}\) response lag time to \(n_{\mathrm{sw}}\) is less than 24 hr. However, Fig. 13a shows that the peak is rather broad, suggesting that the \(j_{e,\mathrm{GEO}}\) response is still significant at \(\tau = 1\) day.
(Fig. 8 from Wing et al. 2016) Blue curve showing (a) \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t) | V_{\mathrm{sw}}(t))\), and (b) \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t) | n_{\mathrm{sw}}(t))\). The solid and dashed green curves are the mean and \(3\tau \) from the mean of the noise. (a) Unlike \(\operatorname{TE}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t))\), which peaks at \(\tau _{\mathrm{max}} = 1\) day, \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t) | V_{\mathrm{sw}}(t))\) peaks at \(\tau _{\mathrm{max}} = 0\) day (\(\mathit{it}_{\mathrm{max}} = 0.091\)). The smaller \(\tau _{\mathrm{max}}\) comes about because CMI removes the effect of \(V_{\mathrm{sw}}\) on \(j_{e,\mathrm{GEO}}\) (see text). (b) The peak in \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t) | n_{\mathrm{sw}}(t))\) (\(\mathit{it}_{\mathrm{max}} = 0.25\)) is broader and has slightly higher snr than that of \(\operatorname{TE}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t))\) in Fig. 13b because CMI removes the effect of \(n_{\mathrm{sw}}\), which anticorrelates with \(j_{e,\mathrm{GEO}}\). \(V_{\mathrm{sw}}\) transfers about 2.7 times more information to \(j_{e,\mathrm{GEO}}\) than \(n_{\mathrm{sw}}\)
Earlier, we established that \(j_{e,\mathrm{GEO}} (t + \text{2 days})\) correlates with \(V_{\mathrm{sw}}(t)\), \(j_{e,\mathrm{GEO}}(t + \text{1 day})\) anticorrelates with \(n_{\mathrm{sw}}(t)\), but \(n_{\mathrm{sw}}(t + \text{1 day})\) anticorrelates with \(V_{\mathrm{sw}}(t)\) (Fig. 12). In Fig. 12d, some of the information in the \(\operatorname{MI}(n_{\mathrm{sw}}, J_{e})\) at \(\tau = 1\text{--}2\) days actually come from \(V_{\mathrm{sw}}\). \(\operatorname{MI}(V_{\mathrm{sw}}, j_{e,\mathrm{GEO}})\) peaks at \(\tau = 2\text{--}3\) days. Because \(V_{\mathrm{sw}}\) anticorrelates with \(n_{\mathrm{sw}}\) at \(\tau = 1\) day, the information in \(\operatorname{MI}(V_{\mathrm{sw}}, j_{e,\mathrm{GEO}})\) at \(\tau = 2\text{--}3\) days would appear in \(\operatorname{MI}(n_{\mathrm{sw}}, j_{e,\mathrm{GEO}})\) at \(\tau = 1\text{--}2\) days. Subtracting this information from \(\operatorname{MI}(n_{\mathrm{sw}}, j_{e,\mathrm{GEO}})\) at \(\tau = 1\text{--}2\) days would allow the \(\operatorname{MI}(n_{\mathrm{sw}}, j_{e,\mathrm{GEO}})\) at \(\tau = 0\) to become the tallest peak, as shown in Fig. 13a. \(\operatorname{MI}(n_{\mathrm{sw}}(t) \rightarrow j_{e,\mathrm{GEO}}(t + \text{1 day}))\) has \(\mathit{it}_{\mathrm{max}} = 0.21\), but removing the effects of \(V_{\mathrm{sw}}\), the \(\mathit{it}_{\mathrm{max}}\) drops ∼57% to 0.091 \([\mathit{it}_{\mathrm{max}}\text{ of } \operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \text{0 day}), n_{\mathrm{sw}}(t)| V_{\mathrm{sw}}(t))\text{ is }0.091]\).
Conversely, some of the effects attributed to \(V_{\mathrm{sw}}\) can be attributed to \(n_{\mathrm{sw}}\), but the effect of \(n_{\mathrm{sw}}\) is smaller. To see this, we calculate \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t) | n_{\mathrm{sw}}(t))\), which is plotted in Fig. 13b as solid blue curve. The blue curve peaks at \(\tau = 2\) days with \(\mathit{it}_{\mathrm{max}} = 0.25\) which is about 2.7 times larger than the \(\mathit{it}_{\mathrm{max}}\) of 0.091 for \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), n_{\mathrm{sw}}(t)| V_{\mathrm{sw}}(t))\). Thus, \(V_{\mathrm{sw}}\) transfers more information to \(j_{e,\mathrm{GEO}}\) than \(n_{\mathrm{sw}}\) does. \(\operatorname{MI}(V_{\mathrm{sw}}(t) \rightarrow j_{e,\mathrm{GEO}}(t + \text{2 days}))\) has \(\mathit{it}_{\mathrm{max}} = 0.32\), but removing the effects of \(n_{\mathrm{sw}}\), the \(\mathit{it}_{\mathrm{max}}\) drops only ∼22% to 0.25 \([\mathit{it}_{\mathrm{max}}\text{ of }\operatorname{CMI}(J_{e}(t + \text{2days}), V_{\mathrm{sw}}(t)| n_{\mathrm{sw}}(t)) = 0.25)]\).
The reason for the broader peak in Fig. 13b is that there is a significant information transfer from \(n_{\mathrm{sw}}\) to \(j_{e,\mathrm{GEO}}\) at \(\tau = 0\text{--}1\) day, but it falls off rapidly at larger \(\tau \). Because the anticorrelation between \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) has a one day lag, removing the effects of \(n_{\mathrm{sw}}\) would lower information transfer from \(V_{\mathrm{sw}}\) to \(j_{e,\mathrm{GEO}}\) (i.e., \(\operatorname{MI}(V_{\mathrm{sw}}(t) \rightarrow j_{e,\mathrm{GEO}}(t + \tau ))\)) at \(\tau = 1\text{--}2\) days. So, \(\mathit{it}\) for \(\operatorname{MI}(V_{\mathrm{sw}}(t) \rightarrow j_{e,\mathrm{GEO}}(t + \tau ))\) at \(\tau = 1, 2, \text{and }3\) are 0.25, 0.32, and 0.23, respectively, whereas the corresponding values for \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t)| n_{\mathrm{sw}}(t)) \) are 0.14, 0.25, and 0.24, respectively. Note that, at \(\tau = 1 \text{ and }2\) there are reductions in information transfer while at \(\tau = 3\), the information transfer is more or less the same (the difference is within one \(\sigma \) [∼0.01]), leading to a broader peak in the \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t)| n_{\mathrm{sw}}(t))\) curve in Fig. 13b than that in the \(\operatorname{MI}(V_{\mathrm{sw}}(t) \rightarrow j_{e,\mathrm{GEO}}(t + \tau ))\) curve in Fig. 12d.
The above analysis suggests that \(V_{\mathrm{sw}}\) is the major driver of \(j_{e,\mathrm{GEO}}\) and places constraints on the \(j_{e,\mathrm{GEO}}\) response time lag to \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\). The process to accelerate the electrons to MeV energy range takes 2–3 days, as previously suggested (e.g., Kellerman and Shprits 2012; Reeves et al. 2011). Moreover, based on information transfer from \(n_{\mathrm{sw}}\) to \(J_{e}\), any mechanism for \(n_{\mathrm{sw}}\) anticorrelation with \(j_{e,\mathrm{GEO}}\) has to operate or start operating within <24 hr.
Next, we investigate whether other solar wind parameters also contribute to \(j_{e,\mathrm{GEO}}\). We calculate the information transfer from \(\mathrm{IMF} |\mathbf{B}|\), \(P_{\mathrm{dyn}}\), \(\sigma (\mathrm{IMF} B)\), southward IMF \(B_{z}\), northward IMF \(B_{z}\), IMF \(B_{y}\), IMF \(B_{x}\), and solar wind electric field (\(E_{\mathrm{sw}}\)) to \(j_{e,\mathrm{GEO}}\), given \(V_{\mathrm{sw}}\). The northward (southward) IMF Bz is calculated from the daily average of the hourly IMF \(B_{z}\) when IMF \(B_{z} > 0\) (IMF \(B_{z} < 0\)). The results are tabulated in Table 1, which ranks various solar wind parameters based on the \(\mathit{it}_{\mathrm{max}}\). Thus, the ranking gives the importance of each solar wind parameter based on the information transfer to \(j_{e,\mathrm{GEO}}\). Table 1 also lists \(\tau _{\mathrm{max}}\) which signifies the lag time when information transfer to \(j_{e,\mathrm{GEO}}\) maximizes.
Note that the ranking in Table 1 is obtained with daily resolution data. It is possible that the ranking of some parameters may change if the data are analyzed at higher time resolution. For example, some studies showed that southward IMF \(B_{z}\) can influence \(j_{e,\mathrm{GEO}}\) (e.g., Li et al. 2005; Onsager et al. 2007; Miyoshi and Kataoka 2008), but southward IMF \(B_{z}\) is only ranked number 5 in Table 1. IMF fluctuates with periods of northward and southward IMF at minutes or tens of minutes timescale. Thus, the low ranking of the southward IMF \(B_{z}\) most likely result from the fluctuations of IMF \(B_{z}\) within one day period (e.g., Li et al. 2001; Balikhin et al. 2011; Reeves et al. 2011). Consistent with our result, Li et al. (2001) found IMF \(B_{z}\) is poorly correlated with \(j_{e,\mathrm{GEO}}\) at daily resolution.
In Fig. 13b, the \(\operatorname{CMI}(j_{e,\mathrm{GEO}}(t + \tau ), V_{\mathrm{sw}}(t)| n_{\mathrm{sw}}(t))\) curve shows that \(V_{\mathrm{sw}}\) has little influence on the geosynchronous MeV electrons after a delay of 7–10 days. Thus, using \(V_{\mathrm{sw}}\), the prediction or information horizon for \(j_{e,\mathrm{GEO}}\) is about 7–10 days. Figure 13a shows that using \(n_{\mathrm{sw}}\), the prediction horizon for \(j_{e,\mathrm{GEO}}\) is about 2 days.
In applying our information theoretical tools, the number of bins (\(n_{b}\)) need to be chosen appropriately. Sturges (1926) proposes that for a normal distribution, optimal \(n_{b} = \log_{2}(n) + 1\) and bin width \((w) = \text{range}/n_{b}\), where \(n\) = number of points in the dataset, range = maximum value – minimum value of the points. In practice, there is usually a range of \(n_{b}\) that would work. Using Sturges (1926) formula, with roughly 6400 points, \(n_{b} \sim 13.6\). For the present study, we find that \(n_{b} = 10\text{ to }15\) would work well. Having too few bins would lump too many points into the same bin, leading to loss of information. Conversely, having too many bins would leave many bins with 0 or a few number of points, which also leads to loss of information. For the present study, we choose \(n_{b} = 10\).
Synoptic View of the Radiation Belts
A distinction between the drivers of the flux dynamics can be obtained by using the impulse response to the solar wind speed \(\mathrm{V}_{\mathrm{SW}}\) as a linear model and comparing its predictions \(\hat{j}_{e} (t;\mathrm{L}; \mathrm{V}_{\mathrm{SW}} )\), where the second argument indicates the solar wind or other driver, with actual measurements of the log-flux \(j_{e} (t;\mathrm{L})\). The data-model correlation for a model driven by speed \(\mathrm{V}_{\mathrm{SW}}\) is defined as:
with notation similar to the correlations above. For the SAMPEX/PET dataset, we obtain the data-model correlation for \(\mathrm{V}_{\mathrm{SW}}\) and compare with 16 other interplanetary, magnetospheric, and solar drivers of the radiation belt electron flux dynamics (Fig. 14).
-
(a)
The data-model correlation for models driven by solar wind speed \(\mathrm{V}_{\mathrm{SW}}\) is indicated by a red thick line; that of a model driven by the dynamic pressure \(\mathrm{P}_{\mathrm{SW}}\) with a red thin line; and that of a model driven by the density \(n_{\mathrm{SW}}\) with an orange dashed line. These three correlations represent the hydrodynamic aspects of the solar wind–magnetosphere interaction. The interaction with the solar wind speed takes place at a longer time scale, many hours to days, than the interaction with the solar wind pressure or density.
-
(b)
Interplanetary inputs \(\mathrm{B}_{\mathrm{South}}\) (blue thick line) and \(\mathrm{V}_{\mathrm{SW}}\mathrm{B}_{\mathrm{South}}\) (blue thin line) and magnetic indices \(\mathrm{K}_{\mathrm{p}}\), \(\mathrm{A}_{\mathrm{p}}\), C9, Dst, AL, AU, and PC (light blue lines) represent the effects of magnetic reconnection such as substorm and storm injections. AL and AU are denoted by dashed lines. These correspond to magnetic interactions between the interplanetary and magnetospheric plasmas and take place rapidly within minutes and hours.
-
(c)
Interplanetary inputs \(\mathrm{B}_{\mathrm{North}}\) (green thick line), \(\mathrm{V}_{\mathrm{SW}}\mathrm{B}_{\mathrm{North}}\) (green thin line), and solar wind quasi-invariant QI as well as solar variables F10.7 and SSN (cyan lines) are interpreted as drivers of electron loss processes.
(Fig. 3 from Vassiliadis et al. 2005) Data-model correlation C(I) (L) from Equation (5.1) for 17 interplanetary/ magnetospheric variables. (top) Solar wind plasma parameters \(\mathrm{V}_{\mathrm{SW}}\) (red thick line), \(\mathrm{P}_{\mathrm{SW}}\) (red thin line), and \(n_{\mathrm{SW}}\) (orange dashed line) represent the hydrodynamic aspects of the solar wind–magnetosphere interaction. (middle) Interplanetary inputs \(\mathrm{B}_{\mathrm{South}}\) (blue thick line) and \(\mathrm{V}_{\mathrm{SW}}\mathrm{B}_{\mathrm{South}}\) (blue thin line) and magnetic indices \(\mathrm{K}_{\mathrm{p}}\), \(\mathrm{A}_{\mathrm{p}}\), C9, Dst, AL, AU, and PC (light blue lines) represent the effects of magnetic reconnection. AL and AU are denoted by dashed lines. (bottom) Interplanetary inputs \(\mathrm{B}_{\mathrm{North}}\) (green thick line), \(\mathrm{V}_{\mathrm{SW}}\mathrm{B}_{\mathrm{North}}\) (green thin line), and solar wind quasi invariant QI as well as solar variables F10.7 and SSN (cyan lines) show the effect of electron losses
5.7 Measuring the Response of the Flux to Solar Wind and Magnetospheric Drivers
Another approach that gives a more precise diagnostic than the correlation is the impulse response function. It assumes a linear, time-invariant relation between an input \(x(t)\) and a resulting output \(y(t)\). Considering the input to be the dominant solar wind driver, i.e., the solar wind speed, and the output to be the flux \(j_{e,\mathrm{GEO}}\) at geosynchronous orbit, we obtain the relation:
where the impulse response function \(h_{\mathrm{GEO}}(\tau )\) captures all the relevant dynamics at a linear approximation. Figure 15a shows this for the log-flux at 3-5 MeV measured by the SEE detector on board spacecraft 1982-2019 from April 1982 to December 1985 (Baker et al. 1990b). a) The negative peak of \(h_{\mathrm{GEO}}(\tau )\) corresponds to the quasiadiabatic displacement of the electrons by the growing inner-magnetospheric field during the storm main phase (the “Dst effect”). b) The positive peak corresponds to the actual acceleration of the electrons peaking 2 days after the solar wind arrival (at \(\tau= 0\) by definition).
(Fig. 12 from Baker et al. 1990b) Impulse response functions of the log-flux to the solar wind speed: (a) at geosynchronous orbit for the log-flux of 3-5 MeV electrons measured by the SEE detector on spacecraft 1982-019. (b) (Fig. 1 from Vassiliadis et al. 2005) as a function of time lag and L shell, as obtained for the log-flux of 2-MeV electrons measured by PET onboard SAMPEX. (c) as a function of time lag and L shell, as obtained from VAP-A/MagEIS in 2015 (Vassiliadis 2019)
We obtain more general representation of the response of the radiation belts to the solar wind speed \(\mathrm{V}_{\mathrm{SW}}\) by parameterizing the response by L shell:
Using data from SAMPEX which scanned the entire L shell range several times per day, we obtain the impulse response (Fig. 15b). In addition to the two peaks \(\mathrm{V}_{0}\) and \(\mathrm{P}_{1}\) familiar from the geosynchronous orbit, we obtain a new peak, P0, in the inner edge of the outer belt, i.e., the shell range L = 3-4. This is in agreement with the block correlation results and indicates a different set of acceleration/loss processes that determine the dynamics in each radiation belt region.
Since SAMPEX is limited due to its orbit and energy range in measuring the electron flux over a range of L shells and energies, we have repeated the analysis with Polar/CEPPAD/HIST electron flux measurements (Vassiliadis 2008) and with VAP/ECT/MagEIS measurements (Vassiliadis 2018, 2019). Figure 15c shows the impulse response function of the MagEIS log-flux to the solar wind velocity. The three peaks \((\mathrm{V}_{1}, \mathrm{P}_{0}, \text{and }\mathrm{P}_{1})\) can be clearly seen. The analysis in terms of correlations and impulse responses shows that there are different sets of acceleration/loss processes acting at these spatial, temporal, and energy ranges.
5.8 Linear and Nonlinear Models
Modeling is an important part of complex systems methods. Equation (5.13) is a linear moving-average (MA) model of the log-flux and can be extended to autoregressive moving-average (ARMA) models (Vassiliadis et al. 1995) and nonlinear autoregressive-moving average models with exogenous parameters (NARMAX) (Balikhin et al. 2011). Selected results of these models are shown in Fig. 16.
(a) and (b): NARMAX model forecast showing measured GEO electron flux in blue and the model estimate in red for > 0:8 MeV and > 2 MeV from January 1 to May 31, 2011 (Fig. 1 from Boynton et al. 2015). (c) Figure (5) from Vassiliadis (2011) shows the outputs of two models (linear vs. nearest-neighbor) developed from the historical SAMPEX/PET 2-MeV flux dataset and applied in predicting the electron flux as a function of L shell during the January 9, 1997 magnetic storm
A different class of nonlinear models are the artificial neural networks (ANNs) and the more recent deep neural networks (DNNs). Selected results of these models are shown in Fig. 17. Early models include (Stringer et al. 1996; Joselyn et al. 1994). More recent ANNs/DNNs for the relativistic-electron flux at GEO have been developed by Ling et al. (2010) and Shin et al. (2016). The relativistic-e flux parameterized by L shell has been modeled by Taylor et al. (2011) using the SAMPEX 2-MeV electron flux. ANNs and DNNs are useful in detecting patterns and have been applied to the classification and detection of spacecraft anomalies (Wintoft et al. 2001). More recent studies of relativistic-electron flux at GEO include modeling with recurrent networks (Fukata et al. 2002).
5.9 Concluding Remarks
We have shown how information theory can be useful in the studies of solar and space physics. Our methodology can generally be applied to a large number of problems because it does not assume a priori the underlying physics of the system. Our findings of information transfer from one parameter to another and the response lag time can provide insights into the physical relationships between the two parameters and provide constraints to models.
In the radiation belt study, the challenge is that several solar wind drivers can affect the radiation belt flux, \(J_{e}\), simultaneously. We show how information theory can be useful to untangle the drivers of the solar wind–radiation belt system, identify causal parameters, and the system response lag times to drivers. One of the conclusions is that the radiation belt electron response lag times to \(V_{\mathrm{sw}}\) and \(n_{\mathrm{sw}}\) are 2 and 0 day, respectively. We show that the nonlinearity and the high variability of \(J_{e}\) in the triangle distribution can be better understood if we take these response time lags into account.
6 How Systems Science Methodology Can Be Used to Assist Physical Understanding: Application to Magnetospheric Dynamical Processes
6.1 Introduction
The traditional approach employed by physicists to advance our knowledge about the world in which we live is to formulate the basic physical principles, gain an understanding of the elementary physical processes and subsequently develop increasingly sophisticated mathematical models for the complex physical objects i.e., a bottom up approach. The underlying assumption of this approach is that once enough experimental/observational data about any complex, natural phenomenon have been collected it is possible to gain a complete physical understanding of this phenomenon and subsequently developed accurate mathematical models to explain its dynamics. This physical approach is based on the premise that, while we are currently unable to fully understand the physics of some complex objects, but with time and more data we will be able to glean the processes involved and to build a mathematical model that will be able to account for any aspects of the dynamics of these objects. This includes sophisticated phenomena and processes such as stem cells, solar-terrestrial system, and even human brain activity. However, often the knowledge that enables the forecast of the evolution of a complex object is required before the thorough from the first principles understanding of physics behind this evolution. Some of the examples are effects of newly developed medicine, evolution of the terrestrial climate and many others including the dynamics of space weather parameters under the solar wind drive.
For complex phenomena that are not yet comprehensively understood from first principles, complementary approaches have been developed within the field of systems science. In some sense, systems science builds the knowledge in the opposite direction to the traditional first principles based approach, i.e., systems science represents a top-down approach. It analyses the overall dynamics of a sophisticated phenomenon by incorporating generic knowledge of the system’s behaviour, and aims to advance our knowledge of the underlying dynamical processes. Therefore, systems science acquires new knowledge from complex to simple, complementary to a traditional approach. In many cases systems science methodologies only aim to provide a reliable forecasting tool that can be used to predict the future evolution of a complex system. However, the most robust techniques developed within this field can also be used to obtain physically interpretable mathematical models of complex phenomena that yield new physical knowledge about them.
The terrestrial magnetosphere is an example of complex system that evolves under the influence of the solar wind. We have achieved colossal advances in our understanding of magnetospheric physics since the start of the space era. We have identified principal processes that are involved in the dynamics of magnetosphere, but from the “system” point of view our knowledge is rather limited. We do not even know the number of degrees of freedom of the magnetosphere. Our current knowledge does not enable us to deduce a quantitative model of the magnetosphere that will allow accurate forecast of space weather parameters from the first principles. We can be confident that in the future, high-quality observations provided by new space missions will make it possible to identify all physical processes that together dynamically drive the magnetosphere and thus our knowledge in a comprehensive first principles based model that could be used for accurate and reliable forecasts of space weather. However, space weather events can harm the critical infrastructure that is vital for a smooth operation of our contemporary society. Reliable forecasts of critical space weather parameters are required now to mitigate effects of possible space weather hazards. There are many examples of systems science-based tools that have been developed to forecast space weather parameters. While these data-based forecasts can greatly assist the mitigation of space weather effects, they have an important shortcoming. Data based models are only reliable if the set of parameters driving the process and their limits are like those used to identify the model. Therefore, the reliability of such models to extreme events such as the Carrington event or the magnetic storms that occurred in May 1921 is unknown since there have been no observational data for events of such magnitude during the era of space measurements and solar wind monitoring. However, it is exactly these extreme events, that could lead to the devastation of modern technological systems, that necessitates their use for space weather forecasting. A thorough understanding of the physics and the ability to create comprehensive quantitative models of the magnetosphere are required to obtain reliable predictions of the effects resulting from such severe space weather events. The application of systems science to space weather can not only result in forecasting tools but also provides insight to advance our physical knowledge about the processes and effects of space weather. The goal of this Section is to illustrate how the powerful systems science methodology can be used to advance the “first principles” based knowledge about the terrestrial magnetosphere.
6.2 System Identification
System identification is a method of dealing with mathematical modeling problems for dynamic systems about which a very limited knowledge of the system internal structure is available. What it is known is that the system is evolving under some external factors that drive its dynamics. For example, in case of the magnetosphere the solar wind is such an external factor. Measurements of these external driving factors are referred to as inputs to the system. In the case of the solar wind and the magnetosphere, the parameters of the solar wind just upstream on the magnetosphere can be considered as inputs to the system. We can also measure some parameters that quantify the response of system, referred to as the system’s outputs, and we assume that these parameters are representative of the state of the system. In the case of the magnetosphere the various geomagnetic indices or fluxes of energetic particles in the inner magnetosphere may be considered as examples of the system outputs. The system is often considered as an unknown input-output “black box” system. However, if some knowledge about the system is available it can be incorporated, and the system is considered as a “grey box”. System identification deals with data sets of system inputs and outputs with the aim to answer different questions such as
-
“How is it possible to predict the evolution of system outputs, if the inputs to the system are known?”
-
“Is it possible to validate first principles based models of the system if the inputs and outputs of the system are known?”
-
“Can a mathematical relation that governs the evolution of the system’s output be deduced directly from data?”
In the simple case of a Linear Time-Invariant (LTI) Single Input-Single Output (SISO) system it is well known that the output \(o ( t )\) is determined by the convolution of the impulse response function \(h_{1} ( t )\) and the input \(i ( t )\):
Equation (6.1) reflects the validity of the superposition principle for linear system. The causality condition requires that \(h_{1} ( \tau ) =0\) if \(\tau <0\). If we have two inputs proportional to the delta functions \(i_{1} \delta ( t- \tau _{1} )\) and \(i_{2} \delta ( t- \tau _{2} )\) the system response \(o ( t )\) will be the sum of the individual responses:
In the case of a continuous input, the convolution integral replaces the summation.
The impulse response function represents the system response when the input is the delta function \(\delta ( t )\). The dynamics of an LTI system is completely characterized by its impulse response function. If \(h_{1} ( t )\) is known, then it is possible to forecast the evolution of output provided that the input is known. The knowledge of \(h_{1} ( t )\) allows a linear mathematical relation that governs the evolution of the system to be deduced and to validate first principles-based models of the system. The Linear Frequency Response Function (LFRF) \(H_{1} ( f )\) is the Fourier transform of \(h_{1} ( t )\). \(H_{1} ( f )\) determines the ratio between the Fourier components of the output \(O ( f )\) and the input \(I ( f )\):
\(H_{1} ( f )\) also, completely defines a linear system. One of the easiest ways to identify a linear SISO system is to use the ratio of the Fourier spectra of the system’s output and input to determine the LFRF and then applying the inverse Fourier transform to calculate \(h_{1} ( t )\). If the system is linear, the ratio of the Fourier spectra of the output and input should not depend upon time, providing a simple test for linearity as demonstrated in the study of geomagnetic activity (Bargatze et al. 1985).
The Volterra decomposition is the generalisation of (6.1) for nonlinear systems:
where \(h_{i} ( \tau _{1}, \tau _{2}, \dots ,\tau _{i} )\) is the \(i\)-th order kernel of the Volterra expansion. The value of \(h_{i} ( \tau _{1}, \tau _{2}, \dots ,\tau _{i} )\) should be zero if the value of any of the arguments is negative because of the causality condition. The second term is simply the convolution integral (6.1) and accounts for the linear part of the system response. To illustrate the process of Volterra decomposition we again consider a simple example with two inputs proportional to the delta function that was used above for a linear system. The superposition principle is not valid in the presence of nonlinearity, so the system response will deviate from the simple sum of \(o_{1} ( t )\) and \(o_{2} ( t )\). In general, this deviation should depend upon relative times of inputs:
Again, when the inputs are continuous signals the sum should be replaced by the integral over all possible values of \(\tau _{1}\)and \(\tau _{2}\). Therefore, the third term of the Volterra expansion reflects the effect of nonlinearity due to all possible pairs of the values of inputs in various times. Similarly, the fourth term in (6.3) is related to the effect of nonlinearity due to all possible triads of the values of input and so on. The infinite set of kernels \(h_{i} ( \tau _{1}, \tau _{2}, \dots ,\tau _{i} )\) completely determines the dynamics of the nonlinear system. In the case of discrete data sets, the integrals in (6.3) are replaced by sums:
The frequency domain representation of the Volterra expansion can be obtained by the multidimensional Fourier transform of (6.4):
where \(H_{i} ( f_{1}, f_{2},\dots , f_{i} )\) is referred to as the \(i\)-th order Generalised Frequency Response Function (GFRF). The 1st order GFRF \(H_{1} ( f )\) has the same physical interpretation as the Linear Frequency Response Function. Its absolute value at a frequency \(f\) determines the growth (attenuation) rate of the corresponding spectral component of the input spectrum at that frequency. The phase of \(H_{1} ( f )\) reflects the speed of the component propagation through the system. \(H_{2} ( f_{1}, f_{2} )\) determines the strengths of the nonlinear coupling between the spectral components \(f_{1}\) and \(f_{2}\) and transfer of their energy to the component \(f= f_{1} + f_{2}\). In the case of plasma systems this corresponds to 3-wave processes, for example the decay instability. Similarly, \(H_{3} ( f_{1}, f_{2}, f_{3} )\) corresponds to 4-wave processes such as a modulational instability. The main problem in the application of Volterra series to real systems is the difficulty to operate with an infinite set of terms and the need to truncate the infinite series to a finite number of (preferably only a few) terms. This can be illustrated using a simple example of the SISO system: \(o ( k ) = i^{2} ( k-1 ) \cdot i ( k-2 ) \cdot o ( k-1 )\). The identification of this system requires the identification of a single term. However, the Volterra-based frequency domain identification will result in an excessive set of GFRFs.
It is known that wave coupling involving more than four waves can be neglected in the case of weak plasma turbulence. Therefore, weak plasma turbulence provides a straightforward justification to truncate Volterra expansion in frequency domain after the third term. System identification methodologies based on truncated Volterra decomposition in the frequency domain have often been applied to study plasma turbulence (Ritz et al. 1989; De Wit et al. 1999; Giagkiozis et al. 2011).
The NARMAX (Nonlinear AutoRegressive Moving Average models with eXogenous inputs) approach, proposed by Leontaritis and Billings (1985a, 1985b) implements methodologies to overcome difficulties of dealing with infinite number of terms of Volterra series.
6.3 NARMAX Approach
The theoretical foundations of NARMAX and overarching description the methodology and key concepts such as the Error Reduction Ratio are provided in Billings et al. (1989) and Billings (2013). In this section, only brief descriptions of the NARMAX approach and the key concept of Error Reduction Ratio is provided based on (Billings et al. 1989; Billings 2013). The basic underlying assumption of the NARMAX is that the value of the output \(o ( k )\) can be expressed as a function (\(F\)) of preceding values of outputs, inputs and noise \(e ( k )\)
where \(l\) is the number of inputs, \(n_{o}, n_{i1},\dots , n_{il}, n_{e}\) are the maximum time lags of the outputs, inputs and noise signal \(e ( t )\). The noise accounts for both impacts of unknown inputs (if any) and measurement errors. The NARMAX approach aims to identify the mathematical form of the function \(F(\dots )\). However, instead of looking for an explicit form of this function, it searches for its decomposition in some basis (e.g., polynomial, wavelet, radial basis functions etc.). Billings et al. (1989) and Billings (2013) provide a comprehensive and mathematically rigorous description of the NARMAX methodology in the general case. Here, a simplified description of the NARMAX approach, that follows Billings (2013) and Boynton et al. (2018a) but limited to the use of a polynomial set of basis functions and not accounting for the error function, is presented. In such a simplified case \(F(\dots )\) is a polynomial function comprising the sum of various monomials \(R_{j} ( k )\) that represent the products of its various arguments. The overall set of monomials includes all possible combinations of these arguments. Therefore, in order to find the function \(F(\dots )\), all unknown constant coefficients \(C_{j}\) in the decomposition (6.7) need to be determined
While the overall aim is to find \(C_{j}\), the initial stage comprises of the search for the coefficients \(T_{j}\) of the auxiliary decomposition:
where \(P_{j} ( k )\) are new set of basis functions resulting from the orthogonalisation of the initial basis \(R_{j} ( k )\). For the new orthogonal basis:
The coefficients \(T_{j}\) can be estimated one by one. If both sides of (6.8) are multiplied by \(P_{l} ( k )\) then the sum of values for all data points can be represented as:
Therefore (Billings et al. 1989)
Once all unknown coefficients are estimated, the decomposition in terms of an orthogonal basis can be subjected to the inverse transform to obtain the coefficients in the original basis \(R_{j} ( k )\). Mathematically the calculations of the coefficients are rather simple. However, in practice the main problem is that the order of nonlinearity of the system is often unknown and strictly the set of monomials \(R_{j}\) should be infinite. Even if the order of nonlinearity is known, the number of monomials can be huge, leading to overfitting problems and a decrease in reliability because the calculations involve measured data that are affected by measurement errors.
If a mathematical model is derived from first principles, the number of independent terms should correspond to the number of degrees of freedom. Similarly, the complexity of a data-derived NARMAX model should mirror the complexity of the system, otherwise the identified system model will not be able to accurately represent the dynamics of the real system. In practical applications, the identification of the NARMAX model involves 3 steps: structure identification, parameter estimation and validation.
The aim of the structure detection is to identify the set of monomial terms that are important for system dynamics. Once such a subset is identified, a simple parameter estimation procedure can then be used to estimate corresponding coefficients \(C_{j} \). After the model is identified it should be validated using data that were not employed in the process of model identification. Validation includes both statistical and dynamical validation. Dynamical validation involves observation of the model dynamics under the same input to a complex system under investigation and assessment of how well the model represents the system. For example, if the model for the Dst index is identified, the comparison of the real Dst index and the evolution of the model output can be used for the dynamical validation. Statistical validation involves several correlation tests developed by Billings and Voon (1986). These statistical tests are able to assess how well the model can account for the variance of the system output, and can also indicate if modifications to the model (e.g., increasing the order of nonlinearity, including extra inputs etc.) are required to create a more accurate representation of the system. The philosophy of NARMAX requires that the developed models should be as simple as possible (Billings 2013). In the beginning a linear model can be considered. However, if the identified model is not able to reproduce the system dynamics with sufficient accuracy, quadratic nonlinearity can be included and so on until the developed model satisfies the correlation tests.
The Forward Regression Orthogonal Least Squares (FROLS) algorithm, developed by Billings et al. (1989), is used for the identification of model structure. This algorithm proceeds as follows. First, if the order of nonlinearity and maximum time lag for the input and the output are defined, the set of monomials (in the case of the polynomial basis functions considered here) is identified. For each element of this set the Error Reduction Ratio (ERR) is calculated:
Taking into account (6.9), it is obvious that \(\mathrm{ERR}_{j}\) quantifies the individual contribution of the basis function \(R_{j}\) to explaining the evolution of \(F(\dots )\), i.e., to evolution of the system’s output. The basis function that corresponds to highest ERR is identified as \(P_{1}\). At the second stage, the subset of remaining basis functions \(R_{l}\) are orthogonalised with respect to \(P_{1}\). For the third stage the ERR is calculated for each element of this orthogonal subset. Again, the element that corresponds to the highest value of ERR is identified and procedure is repeated. Each newly identified basis function accounts for a fraction of the system output variance determined by equation (6.10). The procedure is terminated when the addition of new basis functions does not significantly increase the sum of ERR for previously identified \(P_{l}\). The threshold for the “significance” corresponds to the required accuracy. Once the set of “important” \(P_{l}\) is identified the coefficients \(T_{l}\) are re-estimated. Statistical validation is performed to quantify the quality of the identified model or if the model should be made more complex by increasing the order of nonlinearity or increasing the maximum time lags. The main advantage of NARMAX models is that they are physically interpretable. The explicit mathematical relation resulting from the NARMAX approach can be transformed to frequency domain. If the system is linear the transformation of the model to frequency domain will display features corresponding to the Linear Frequency Response function such as resonances, providing important information about physical processes involved. For nonlinear systems, the resonances are replaced by other features in the GFRFs such as “ridges” that similarly are able to provide information about the physics of the system (Billings 2013).
There is another beneficial aspect of model representation in frequency domain. Even simple mathematical expressions in continuous form can correspond to non-unique expressions in discrete form. For example, central, forward or backward finite-difference methods will lead to distinct polynomial representations of the third derivative. Similarly, if polynomial representations of the system’s model are distinct, it does not mean that they are not equivalent or do not represent the same dynamics. In the time domain, it is often not a very easy task to show similarity of two discrete models representing the same system. However, if both models accurately represent the system’s dynamics their transformation to frequency domain should lead to very similar structures of GFRFs. This was done in first applications of the NARMAX approach to the modeling of the Dst index (Boaghe et al. 2001).
6.4 Quest for Inputs
One of the first questions that should be answered in the study of a complex natural dynamical system is: What are the external factors that drive the evolution of this system? The knowledge of these external drivers is key for both the traditional first principles based and for the systems science approaches. If these external factors are not known, it is impossible to develop a first principles based mathematical model of the system’s dynamics or to apply a black box approach. In the case of the terrestrial magnetosphere, it has been known for a long time that the solar wind is the main driver of its dynamics. However, not all parameters of the solar wind will have a significant effect on the magnetosphere. For example, under normal conditions the proton temperature is usually “forgotten” after the solar wind has traversed the bow shock and therefore cannot have a notable influence on the dynamics of the magnetosphere. The quest to determine which of the solar wind parameters or their combination play a key role in the dynamics of the magnetosphere dates back to the early days of space physics (Chapman and Ferraro 1931). These solar wind inputs are referred to as Solar wind – Magnetosphere Coupling Functions (CFs). Chapman and Ferraro (1931) suggested that the solar wind dynamic pressure is the most probable candidate for the CF. Early first principles based studies considered diverse factors that may affect geomagnetic activity including lunar phases and positions of Mercury and Venus (e.g., Bigg 1963). The concept of the merging of magnetic fields (Dungey 1961) and progress in our comprehension of magnetic reconnection phenomenon led to an understanding of the importance of the southward IMF component \(B_{s}\) in geomagnetic activity. The half-wave rectifier \(vB_{s}\) (\(v\) is the solar wind speed) was proposed by Burton et al. (1975) as another possible CF.
Perreault and Akasofu (1978) argued that the CF should be related to the solar wind input energy flux. They proposed the product of the magnetic energy flux \(v B^{2}\), the effective length of the reconnection line \(l_{0}\) squared and the angle factor (\(\varepsilon \)-function) as a CF:
where \(\theta \) is the polar angle of the IMF in the Y-Z (GSM) plane. Kan and Lee (1979) developed a theoretical justification for (6.11) as a CF. Considerations of the dimensionality have led to the proposal by Vasyliunas et al. (1982) of other mathematical forms for CF. With time, first-principles based studies resulted in a significant growth of the set of possible expressions for solar wind-magnetosphere CFs. For example, about 20 different mathematical relations for CFs have been investigated by Newell et al. (2007). For a long time, the assessment of the appropriateness of a CF involved its correlation with geomagnetic indices. This approach could, however, be misleading because only linear dependences between two data sets can be assessed by the correlation function. In the case of a nonlinear system, the correlation between the input and output can be very low. The standard example is a simple quadratic system \(o ( t_{k} ) = i^{2} ( t_{k-1} )\) driven by a zero-mean input \(i\). A technique that is relevant for not only linear but also nonlinear relations should be used to assess the potential of a particular version of the coupling function. The concept of ERR, that accounts for both linear and nonlinear dependences, has been applied to investigate the forecasting abilities of various previously proposed CFs (Balikhin et al. 2010; Boynton et al. 2011): \(V B_{s}\) (Burton et al. 1975); \(\varepsilon =v B^{2} \sin ( \frac{\theta}{2} )^{4}\) (Perreault and Akasofu 1978); \(C_{W} =v B_{T}^{2} \sin ( \frac{\theta}{2} )^{6}\), (Wygant et al. 1983); \(C_{SR} =p^{\frac{1}{2}} v B_{T} \sin ( \frac{\theta}{2} )^{4}\) (Scurry and Russell 1991); \(C_{N} =v^{\frac{4}{3}} B_{T}^{{2} / {3}} \sin ( \frac{\theta}{2} )^{{8} / {3}}\), (Newell et al. 2007); \(C_{V} =n^{\frac{1}{6}} v^{\frac{4}{3}} B_{T} G ( \theta )\) (Vasyliunas et al. 1982) where \(B_{T} = \sqrt{B_{y}^{2} + B_{z}^{2}}\).
In addition to the CFs derived from first principles, the data based CF developed by Temerin and Li (2006) \(C_{TL} =p^{\frac{1}{2}} v B_{T} \sin ( \frac{\theta}{2} )^{6}\) (where \(B_{T} = \sqrt{B_{y}^{2} + B_{z}^{2}}\)) is also included in the list. The data sets used by Balikhin et al. (2010) and Boynton et al. (2011) to employ the ERR technique to identify the most effective CF included about 11 years (from the start 1998 to the end of 2008) of solar wind data from the OMNI website (http://omniweb.gsfc.nasa.gov/ow_min.html) and \(\mathrm{Dst}\) values for the same period. The application of the NARMAX methodology usually requires continuous data sets of inputs and outputs. Typically, if data are not oversampled, about 1000 pairs of input-output measurements are required for the successful application of NARMAX. The 11 years of solar wind data obtained from the OMNI website contained a few data gaps. A set of 64 subintervals without data gaps that contained at least 1000 data points were identified within the 11-year interval. The set of possible inputs included all CFs listed above and previous values of “\(\mathrm{Dst}\)”. ERRs for terms corresponding to five possible time lags from \(t-1\) to \(t-5\) for each input were calculated in (Boynton et al. 2011). It is well known that the value of \(\mathrm{Dst} ( t-1 )\) has a very strong effect on the value of \(\mathrm{Dst} ( t )\). Indeed, the mean over all 64 intervals of the ERR corresponding to term \(\mathrm{Dst} ( t-1 )\) (Boynton et al. 2011) was 95.5% with a standard deviation 2.13%. The quest for the best coupling function is the quest for the solar wind parameter that possesses the strongest potential for the forecast of geomagnetic disturbances. While statistically the persistence model can account for major part of Dst variance, and will provide an accurate the significant fraction of time, it will fail at times when a quiet period gives way to a geomagnetic storm. Therefore, while the input parameter \(\mathrm{Dst} ( t-1 )\) accounts for about 95% of the \(\mathrm{Dst} ( t )\) variance the quest for the coupling function should aim to determine to the parameter that accounts for the highest fraction of remaining variance. Boynton et al. (2011) introduced the concept of Normalized ERR:
where \(\mathrm{ERR}_{C}\) and \(\mathrm{NERR}_{C}\) are ERR and NERR corresponding to the input parameter \(C\) and \(S\) is the sum of ERR values for all inputs included into study. Therefore, the sum of all NERRs for all inputs except \(\mathrm{Dst} ( t-1 )\) for any subinterval should be equal to \(100 \%\). The five coupling functions with the highest NERR and corresponding values of NERR as obtained by Boynton et al. (2011) are given in Table 2 (from Boynton et al. 2011, Table 3). The values of NERR in this table are the result of averaging over all 64 subintervals. It can be seen that \(C_{TL}\), the CF identified by Temerin and Li (2006), has the highest NERR value 31.32% while the second highest value corresponds to \(v B_{s} ( t-1 )\) and is equal to 12.76%, indicating a sharp decrease in the forecasting abilities in comparison to \(C_{TL} \). There is a clear difference in the NERR values between first and second CFs in the table but the other are fairly similar 10.30% for CF suggested by Vasyliunas et al. (1982) and 7.23% for \(\operatorname{Dst} ( t-2 )\).
As explained above, the NARMAX approach can be used to combine input monomials to maximise the ERR values. To capitalize on this advantage of NARMAX Boynton et al. (2011) decomposed the 5 coupling functions in Table 3 into individual factors.
This resulted in the following set of factors \(p^{\frac{1}{2}}\), \(n^{\frac{1}{6}}\), \(v\), \(v^{\frac{4}{3}}\), \(B_{s}\), \(B_{T} \sin^{4} ( \frac{\theta}{2} )\), \(B_{T} \sin^{6} ( \frac{\theta}{2} )\).
Boynton et al. (2011) imposed the 4th order limit on the monomials composed of these factors to constrain required computational resources. The factors \(B_{T} \sin^{4} ( \frac{\theta}{2} )\) and \(B_{T} \sin^{6} ( \frac{\theta}{2} )\) were included instead of \(B_{T}\) and \(\sin ( \frac{\theta}{2} )\) because of this imposed limitation.
Three top coupling functions with the highest values of NERR include the factor \(\sin ( \frac{\theta}{2} )^{6}\). While this power of \(\sin ( \frac{\theta}{2} )\) was identified empirically by Temerin and Li (2006), it differs from the factor \(\sin ( \frac{\theta}{2} )^{4}\) deduced from first principles by Kan and Lee (1979).
The NARMAX ability to provide physically interpretable results motivated Balikhin et al. (2010) to re-visit the derivation of \(\varepsilon \) by Kan and Lee (1979). The geometry of the model is illustrated in Fig. 18 from Kan and Lee (1979) where it was assumed that the magnetosheath magnetic field \(B_{s}\) and the magnetospheric magnetic field \(B_{m}\) have the same magnitude but different directions. Kan and Lee (1979) used an expression for the reconnection electric field \(E_{r}\) derived by Sonnerup (1974):
where \(v_{s}\) is the component of the magnetosheath plasma velocity in the direction normal to \(B_{s}\). Kan and Lee (1979) noted that \(\theta =\theta '\) on the noon-midnight meridian, but they can differ along the reconnection line. However, the approximation \(\theta =\theta '\) was used in their model. \(E_{r}\) is parallel to the reconnection line and is the only component of the magnetosheath electric field “impressed by the reconnection on open field lines inside the magnetosphere” (Kan and Lee 1979). On the magnetospheric side \(E_{r}\) has both parallel \(E_{\parallel} \) and perpendicular \(E_{\bot} \) components with respect to the magnetic field. Kan and Lee (1979) stated that only \(E_{\bot} = E_{r} \sin ( \frac{\theta}{2} )\) contributes to the potential difference across the polar cap \(\varPhi \):
where the integration is along the reconnection line, \(B\), \(E\), \(l_{0}\) represent the beginning, the end and the length of the reconnection line.
(Fig. 1 from Kan and Lee 1979). Verbatim [Kan and Lee 1979] “Fig. 1. A schematic illustration of the field line reconnection geometry. (a) An illustration of how the orientation of the X line is determined. The circle is used to illustrate the assumed equality in magnitudes of \(B_{m}\) and \(B_{s}\). The solar wind velocity is normal to the plane. The orientation of the X line is chosen so that the field component parallel to the X line is uniform across the magnetopause. (b) An illustration of the equipotentials (dashed lines) of the reconnection electric field. A component of the reconnection electric field is parallel to the reconnected field lines inside the magnetopause”
According to (Kan and Lee 1979) model the power produced by the solar wind dynamo \(P\) is
where \(R\) is the “equivalent resistance” connected to the solar wind magnetospheric dynamo. Therefore, according to Kan and Lee (1979) model the factor \(\sin ( \frac{\theta}{2} )\) should enter the coupling function with the power 6, i.e., the same power as was identified by the ERR approach (Balikhin et al. 2010). The power 4 of this factor in Kan and Lee (1979) is the result of the miscalculation of the integral (5.11). Since the \(E_{\bot} \) component is not parallel to the reconnection line \(E_{\bot} dl= E_{\bot} dl\ \sin ( \frac{\theta}{2} )\) and this extra factor \(\sin ( \frac{\theta}{2} )\) appears to have been missed. Thus, the interpretation of the results of the NARMAX ERR approach was able to deduce the mathematical form of the factor that is missing in derivation by Kan and Lee (1979).
The NARMAX and related linear methodologies can be extended to other equally powerful approaches. Instead of using global functions of the state and input variables as evidenced in the LTI and NARMAX models, an approach that uses local functions of the state is the local-linear model (Vassiliadis et al. 1995; Klimas et al. 1997, 1998). A local-linear ARMA model is obtained from a parameter estimation approach applied to a region of the state space instead of the entire space (Farmer and Sidorowich 1987; Vassiliadis et al. 1995). The procedure is repeated for other regions to cover all observed dynamics.
Klimas et al. (1997) showed how to map the local-linear ARMA model to a nonlinear, continuous-time analogue by transforming both to the frequency domain and mapping their transfer functions. The continuous-time analogue is capable of the same dynamics as the discrete-time model, and in addition having a clearer physical interpretation. In that work and its continuation (Klimas et al. 1998), several examples were shown based on the Dst index and solar wind CFs such as the \(vB_{s}\) product where \(B_{s}\) is the Southward IMF component mentioned earlier. The resulting general model for Dst is a damped, nonlinear oscillator in good agreement with the Burton et al. (1975) model derived using a different, phenomenological approach. The dynamics of the model, such as strong coupling to the solar wind CF before and during the storm main phase and uncoupling during storm recovery, provide a solid physical interpretation of the large-scale dynamics of the ring current amplitude as represented by the ground-based index Dst. The nonlinearity of the model can be adjusted by applying the parameter estimation to a large time window, representative of a broad region of the state space and the slower dynamics vs. a narrow window which is more representative of the more detailed variations of the index.
The application of systems science to the successful search of external parameters that are effective in governing evolution of complex dynamical system has stimulated other magnetospheric modeling problems such as the evolution of fluxes of energetic electrons at the geostationary orbit (Boynton et al. 2013) and spatio-temporal distributions of key wave emissions in the inner magnetosphere such as hiss, equatorial magnetosonic waves and lower band chorus (Boynton et al. 2018b).
The radiation belts or Van Allen belts were discovered by the very first in situ observations of the space era. Occupying the equatorial region between approximately 1.2 and 7-8 \(\mathrm{R}_{\mathrm{e}}\) the radiation belts are characterized by large numbers of high energy particles which may pose a threat to the communications, navigational, and other satellites whose orbits either cross this region or are located in Geostationary orbit (GEO). While the inner radiation belt is relatively stable, in the outer radiation belt the fluxes of highly energetic electrons can vary by a few orders of magnitude on time scales of a few hours. More than half a century after their discovery our understanding of the dynamics of the radiation belts is far from complete. The energisation of radiation belt electrons is usually attributed to two main processes, namely radial diffusion and the local interaction of particles with waves such as chorus. The relative efficiency of these processes can depend upon the location within the radiation belts. There are many arguments in favour of the fact that in the central part of the outer radiation belt (4-5.5 \(\mathrm{R}_{\mathrm{e}}\)) the interaction with waves is the dominant acceleration process and radial diffusion only plays a minor role (Shprits et al. 2008). However, the relative importance of these two processes can be different at the outskirts of the outer radiation belt where GEO is located (∼6.6 \(\mathrm{R}_{\mathrm{e}}\)). The advantage of GEO for applications of systems science methods is that continuous data sets are available. Application of the ERR to electron flux measurements at GEO allowed Balikhin et al. (2012) and Boynton et al. (2013) to show that the dynamics of electron fluxes at GEO is incompatible with acceleration models based on local quasilinear interaction with waves. Below the study of Boynton et al. (2013) is briefly reviewed.
This study was based on data obtained during the 7405 day period (09/22/1989-12/31/2009) by the Los Alamos National Laboratory Synchronous Orbit Particle Analyzer (SOPA) instruments (Reeves et al. 2011). The methodology that has been used to evaluate the fluxes of energetic electrons at 13 fixed virtual energy channels in the range from 24.1 keV to 2 MeV (24.1. keV, 31.7 keV, 41.6 keV, 62.5 keV, 90.0 keV, 127.5 keV, 172.5 keV, 270.0 keV, 407.5 keV, 625 keV, 925 keV, 1.3 MeV, 2.0 MeV) is described in Reeves et al. (2011) and Cayton and Tuszewski (2005). The data for the electron flux in the energy range 1.8-3.5 MeV are obtained by the Energetic Sensor for Particles (ESP). The resulting data sets have been published by Reeves et al. (2011) and are available as the auxiliary material for their paper at ftp://ftp.agu.org/apend/ja/2010ja015735, together with an overview of the data preparation methodology. These 14 data sets of the daily averages fluxes were treated as the outputs of a “black box” system. The input data set included daily averaged values for GSM components of the interplanetary magnetic field, solar wind density, velocity and dynamic pressure. The daily averaged solar wind data at L1 were downloaded from the OMNI web site. Since the NARMAX approach requires continuous data sets, linear interpolation was used in Boynton et al. (2013) to fill data gaps with less than 6 missing data points in the input and output data sets. As a result, 8 continuous subsets that contained at least 250 data points were identified. All together these 8 subsets contained 6076 days or about 82% of the original data set.
The results of ERR analysis by Boynton et al. (2013) is summarised in the Table 4. Each row corresponds to a particular energy range. For each energy range the top four terms with the highest ERR are shown. The two numbers in brackets after each term are the corresponding value of ERR averaged over the 8 data subsets and the number of data subsets for which that the term was selected. It can be seen from Table 4 that the velocity of the solar wind is the most effective control parameter at all energies except for the two highest ranges 2.0 MeV and 1.8-3.5 MeV. The velocity terms account for more than 96% of flux variations for the energy ranges from 2.4 to 925 keV. For these energy ranges the top velocity terms have been selected for all 8 intervals. However, as can be seen from Table 4 the time delay corresponding to the solar wind velocity measurements that accounts for most of the variance in the electron flux measurements depends upon the energy range. For lower energy ranges, up to 90 keV, the fluxes are mostly controlled by the value of solar velocity on the same day. This accounts for more than 97% of the flux variance for these energy ranges. The contribution of all other terms is negligible. However, for the energy range 127.5 keV the value of velocity on the same day accounts for only for 74.9% of the variance. For this energy range the velocity measured on the previous day \(v ( t-1 )\) provides substantial contribution of about 22%. As the energy range increase, further to 172.5 keV the role of the solar wind velocity on the previous day becomes the dominant factor, accounting for 65.7% of the variance while velocity on the same day accounts only for about 31.6% of the variance. For the next energy range of 270 keV \(v ( t-1 )\) terms account for more than 99% of the flux variance and contribution of all other factors including the solar wind velocity on the same day can be neglected. For energy ranges 407.5 keV and 625.0 keV the solar wind velocity on the previous day remains the dominant factor that controls fluxes, however the contributions from \(v ( t-2 )\) become increasingly more significant at levels of 13.7% and 22.2% respectively. Finally, for the energy range 925 keV the term \(v ( t-2 )\) accounts for 96% of variance, while the contributions of all other terms can be neglected. The dependence between the energy of accelerated electrons and the time that is required for the solar wind to affect this energy range has been observed previously (e.g., Li 2004). The acceleration model, based on the quasilinear interaction with magnetospheric waves, naturally leads to a monotonic dependence between time and energy. Quasilinear diffusion of the seed population will lead to the emergence of an electron population with slightly higher energies. This newly formed population will undergo quasilinear interactions, leading to the formation of a more energetic population and so on. Qualitatively, quasilinear diffusion should lead to a monotonic dependence between the time delay and the energy range. In simple diffusion processes, this dependence should be close to the dependence of the Brownian displacement upon time and proportional to the square root of the time. The results from the ERR analysis presented in Table 4 have been used to calculate the effective time delay \(\tau _{E\mathrm{eff}}\) for the reaction of electron fluxes at a particular energy \(E\) to the velocity of the solar wind (Boynton et al. 2013):
where \(d_{Ej}\) is the sum of ERR values for the energy \(E\) of all terms that include \(v ( t-j )\). Figure 19 taken from Boynton et al. (2013) displays the resulting dependence of \(E(\tau _{E\mathrm{eff}} )\). It can be seen from Fig. 19 that the energy increase occurs significantly faster than \(\sqrt{\tau _{E\mathrm{eff}}}\) expected for a simple Brownian process.
(Fig. 1 from Boynton et al. 2013) Dependence of the energy range upon the time delay
The energy diffusion equation (6.16) (Horne et al. 2005) that describes the effect of wave particle interactions in the magnetosphere is similar but also more complex than that describing a simple Brownian process:
where \(A ( E ) = ( E+ E_{0} ) ( E+2 E_{0} )^{\frac{1}{2}} E^{\frac{1}{2}}\), \(F ( E, \alpha _{eq} )\) is the electron distribution function which depends upon energy and equatorial pitch angle, \(E_{0} =m c^{2}\) is the electron rest energy, \(D\) is the bounce-averaged energy diffusion coefficient and \(\tau _{L}\) is the characteristic timescale for atmospheric loses.
The distribution function \(F ( E, \alpha _{eq} )\) of the electron fluxes \(J ( E, \alpha _{eq} )\) may be relativistically expressed as (Horne et al. 2005):
Balikhin et al. (2012) used (6.16) to determine the analytical dependence of fluxes upon time for three different energy regimes (1) \(E \ll E_{0}\); (2) \(E \approx E_{0}\); and (3) \(E \gg E_{0}\) and showed that in all three regimes the time required for the formation of more energetic electron populations still exhibits a dependence close to \(\sqrt{\tau _{E\mathrm{eff}}}\) that is characteristic of a diffusion process. In this derivation Balikhin et al. (2012) used a few simplifying assumptions. The derivation was performed separately for all energy regimes and for each regime it was assumed that \(D\) does not depend upon energy. The gradient of \(E(\tau _{E\mathrm{eff}} )\) from Fig. 19 is about 1.5 (if the lowest energy value 127.5 keV is not taken into account) or 1.05 if all points are considered. Both values significantly exceed 0.5 that would be expected from a \(\sqrt{\tau _{E\mathrm{eff}}}\) dependence. This result allowed Boynton et al. (2013), to conclude that quasilinear interaction with local waves is not the dominant acceleration process at GEO. They suggested that the increase of fluxes of energetic electrons at GEO is the result of outward radial diffusion from central regions of the radiation belts where local wave-particle interaction is the dominant acceleration process.
In contrast to the lower energy ranges for which the effect of terms that do not include the solar wind velocity are negligible, the fluxes at higher energies (2 MeV and 1.8-3.5 MeV) are more dependent on the previous day’s solar wind density. While higher velocity leads to the increase in fluxes, higher densities lead to the decrease of fluxes.
6.5 Concluding Remarks
While the most frequent application of systems science in solar terrestrial physics is the development of space weather forecasting tools, the most powerful systems science methodologies can also yield advances in our understanding of the underlying physics. Examples of the identification of a system’s input parameters were presented in this Section. Much more complicated methodologies include the use of GFRFs to develop frequency domain models of an unknown system and their interpretation. Further techniques enable the reconstruction of integro-differential continuous equations that relate the inputs of a system to its outputs. These data-based modeling results may also be compared to models derived from analytical first principles based considerations.
7 Outlook
Herein we have provided an essential overview on existing nonlinear dynamical systems-based methodologies along with key results of their previous application in a space physics context, thus illustrating how complementary modern complex systems approaches have recently shaped our understanding of nonlinear magnetospheric variability.
There is a series of immediate next steps for future work inspired by the present initiative, which can be outlined in the following objectives:
-
Which are the most efficient and versatile diagnostic approaches and schemes based on these methods that can be transitioned into reliable space weather forecasting tools?
-
Which ongoing open research questions would benefit from in-depth investigations from complex systems viewpoint, and which existing methods or combinations thereof would be appropriate for tackling them?
-
Specifically, how can these methods be utilized to efficiently integrate information from various data sources (satellites, ground magnetometers, models, etc.) in the presence of multiple interacting temporal and spatial scales, variables and processes that are relevant for the variability of the geomagnetic field?
Given the currently available enormous amounts of space-related datasets (e.g., solar wind data, magnetospheric and ionospheric satellite data, ground-based observatory data, geomagnetic activity indices data), nonlinear dynamical systems methods have the potential to treat combined data from the various sources in a unique way, providing valuable information about the spatial and temporal evolution along with the underlying physical processes of the near-Earth electromagnetic environment.
Data Availability
All the derived data products in this paper are available upon request by email (simon.wing@jhuapl.edu; dimitris.vassiliadis2000@gmail.com).
References
Addison PS (2017) The illustrated wavelet transform handbook: introductory theory and applications in science, engineering, medicine and finance. CRC Press, Boca Raton
Akasofu S-I (1964) The development of the auroral substorm. Planet Space Sci 12:273–282
Akasofu S-I (2016) Personal communication with B.T. Tsurutani
Al-Sharhan S, Karray F, Gueaieb W, Basir O (2001) Fuzzy entropy: a brief survey. In: 10th IEEE international conference on fuzzy systems, Cat. No. 01CH37297, vol 3, pp 1135–1139. https://doi.org/10.1109/FUZZ.2001.1008855
Alberti T, Lepreti F, Vecchio A, Bevacqua E, Capparelli V, Carbone V (2014) Natural periodicities and Northern Hemisphere-Southern Hemisphere connection of fast temperature changes during the last glacial period: EPICA and NGRIP revisited. Clim Past 10:1751–1762
Alberti T, Consolini G, Lepreti F, Laurenza M, Vecchio A, Carbone V (2017) Timescale separation in the solar wind-magnetosphere coupling during St. Patrick’s Day storms in 2013 and 2015. J Geophys Res Space Phys 122(4):4266–4283. https://doi.org/10.1002/2016JA023175
Alberti T, Consolini G, De Michelis P, Laurenza M, Marcucci MF (2018) J Space Weather Space Clim 8:A56. https://doi.org/10.1051/swsc/2018039
Alberti T, Consolini G, Ditlevsen PD, Donner RV, Quattrociocchi V (2020a) Multiscale measures of phase-space trajectories. Chaos 30:123116. https://doi.org/10.1063/5.0008916
Alberti T, Lekscha J, Consolini G, De Michelis P, Donner RV (2020b) Disentangling nonlinear geomagnetic variability during magnetic storms and quiescence by timescale dependent recurrence properties. J Space Weather Space Clim 10:25
Alberti T, Faranda D, Consolini G, Di Michelis P, Donner RV, Carbone V (2022) Concurrent effects between geomagnetic storms and magnetospheric substorms. Universe 8:226
Allen MR, Robertson AW (1996) Distinguishing modulated oscillations from coloured noise in multivariate datasets. Clim Dyn 12:775
Allen MR, Smith LA (1994) Investigating the origins and significance of low-frequency modes of climate variability. Geophys Res Lett 21(10):883
Allen MR, Smith LA (1996) Monte Carlo SSA: detecting irregular oscillations in the presence of colored noise. J Climate 9(12):3373
Andriyas T, Andriyas S (2017) Periodicities in solar wind-magnetosphere coupling functions and geomagnetic activity during the past solar cycles. Astrophys Space Sci 362:160. https://doi.org/10.1007/s10509-017-3141-9
Araki T, Tsunomura S, Kikuchi T (2009) Local time variation of the amplitude of geomagnetic sudden commencements (SC) and SC-associated polar cap potential. Earth Planets Space 61:e13–e16
Archer MO, Hartinger MD, Horbury TS (2013) Magnetospheric ‘magic’ frequencies as magnetopause surface eigenmodes. Geophys Res Lett 40:5003
Bak P, Tang C, Wiesenfeld K (1987) Self-organized criticality: an explanation of the 1/f noise. Phys Rev Lett 59:381
Bak P, Tang C, Wiesenfeld K (1988) Self-organized criticality. Phys Rev A 38:364–374
Baker DN (2020) Solar-terrestrial data science: prior experience and future prospects. Front Astron Space Sci 7:540133. https://doi.org/10.3389/fspas.2020.540133
Baker DN, Kanekal SG (2008) Solar cycle changes, geomagnetic variations, and energetic particle properties in the inner magnetosphere. J Atmos Sol-Terr Phys 70:195–206. https://doi.org/10.1016/j.jastp.2007.08.031
Baker DN, Klimas AJ, McPherron RL, Buechner J (1990a) The evolution from weak to strong geomagnetic activity: an interpretation in terms of deterministic chaos. Geophys Res Lett 17(1):41–44
Baker DN, McPherron RL, Cayton TE, Klebesadel RW (1990b) Linear prediction filter analysis of relativistic electron properties at 6.6 \(\mathrm{R}_{\mathrm{E}}\). J Geophys Res 95(A9):15133–15140. https://doi.org/10.1029/JA095iA09p15133
Balasis G, Egbert GD (2006) Empirical orthogonal function analysis of magnetic observatory data: further evidence for non-axisymmetric magnetospheric sources for satellite induction studies. Geophys Res Lett 33:L11311. https://doi.org/10.1029/2006GL025721
Balasis G, Daglis IA, Kapiris P, Mandea M, Vassiliadis D, Eftaxias K (2006) From pre-storm activity to magnetic storms: a transition described in terms of fractal dynamics. Ann Geophys 24:3557–3567
Balasis G, Daglis IA, Papadimitriou C, Kalimeri M, Anastasiadis A, Eftaxias K (2008) Dynamical complexity in Dst time series using nonextensive Tsallis entropy. Geophys Res Lett 35:L14102. https://doi.org/10.1029/2008GL034743
Balasis G, Daglis IA, Papadimitriou C, Kalimeri M, Anastasiadis A, Eftaxias K (2009) Investigating dynamical complexity in the magnetosphere using various entropy measures. J Geophys Res 114:A00D06. https://doi.org/10.1029/2008JA014035
Balasis G, Daglis IA, Papadimitriou C, Anastasiadis A, Sandberg I, Eftaxias K (2011b) Quantifying dynamical complexity of magnetic storms and solar flares via nonextensive Tsallis entropy. Entropy 13(10):1865–1881
Balasis G, Papadimitriou C, Daglis IA, Anastasiadis A, Athanasopoulou L, Eftaxias K (2011a) Signatures of discrete scale invariance in Dst time series. Geophys Res Lett 38:L13103. https://doi.org/10.1029/2011GL048019
Balasis G, Donner RV, Potirakis SM, Runge J, Papadimitriou C, Daglis IA, Eftaxias K, Kurths J (2013) Statistical mechanics and information-theoretic perspectives on complexity in the Earth system. Entropy 15(11):4844–4888. https://doi.org/10.3390/e15114844
Balasis G, Potirakis SM, Mandea M (2016) Investigating dynamical complexity of geomagnetic jerks using various entropy measures. Front Earth Sci 4:71
Balasis G, Daglis IA, Contoyiannis Y, Potirakis SM, Papadimitriou C, Melis NS et al. (2018) Observation of intermittency-induced critical dynamics in geomagnetic field time series prior to the intense magnetic storms of March. J Geophys Res Space Phys 123:4594–4613. https://doi.org/10.1002/2017JA025131
Balasis G, Papadimitriou C, Boutsi AZ, Daglis IA, Giannakis O, Anastasiadis A, De Michelis P, Consolini G (2020) Dynamical complexity in Swarm electron density time series using block entropy. Europhys Lett 131:69001. https://doi.org/10.1209/0295-5075/131/69001
Balikhin MA, Boynton RJ, Billings SA, Gedalin M, Ganushkina N, Coca D, Wei H (2010) Data based quest for solar wind-magnetosphere coupling function. Geophys Res Lett 37:L24107. https://doi.org/10.1029/2010GL045733
Balikhin MA, Boynton RJ, Walker SN, Borovsky JE, Billings SA, Wei HL (2011) Using the NARMAX approach to model the evolution of energetic electrons fluxes at geostationary orbit. Geophys Res Lett 38:L18105. https://doi.org/10.1029/2011GL048980
Balikhin MA, Gedalin M, Reeves GD, Boynton RJ, Billings SA (2012) Time scaling of the electron flux increase at GEO: the local energy diffusion model vs observations. J Geophys Res 117:A10208. https://doi.org/10.1029/2012JA018114
Bandt C, Pompe B (2002) Permutation entropy: a natural complexity measure for time series. Phys Rev Lett 88(17):174102. https://doi.org/10.1103/PhysRevLett.88.174102
Bargatze LF, Baker DN, McPherron RL, Hones EW Jr (1985) Magnetospheric impulse response for many levels of geomagnetic activity. J Geophys Res 90:6387
Belian RD, Gisler GR, Cayton T, Christensen R (1992) High-Z energetic particles at geosynchronous orbit during the Great Solar Proton Event Series of October 1989. J Geophys Res 97(A11):16897–16906. https://doi.org/10.1029/92JA01139
Bigg EK (1963) Lunar and planetary influences on geomagnetic disturbances. J Geophys Res 68:4099
Billings SA (2013) Nonlinear system identification: NARMAX methods in the time, frequency, and spatio-temporal domains. Wiley, New York
Billings SA, Voon WSF (1986) Correlation based model validity tests for non-linear models. Int J Control 44:235–244
Billings SA, Chen S, Korenberg MJ (1989) Identification of MIMO non-linear systems using a forward regression orthogonal estimator. Int J Control 49:2157–2189
Billingsley P (1965) Ergodic theory and information. Wiley, New York
Boaghe OM, Balikhin MA, Billings SA, Alleyne H (2001) Identification of nonlinear processes in the magnetospheric dynamics and forecasting of Dst index. J Geophys Res 106:30047–30066
Borovsky JE (2013) Physical improvements to the solar wind reconnection control function for the Earth’s magnetosphere. J Geophys Res Space Phys 118:2113–2121. https://doi.org/10.1002/jgra.50110
Borovsky JE (2021) Is our understanding of solar-wind/magnetosphere coupling satisfactory? Front Astron Space Sci 8:634073
Borovsky JE, Funsten HO (2003) MHD turbulence in the Earth’s plasma sheet: dynamics, dissipation and driving. J Geophys Res 108(A7):1284. https://doi.org/10.1029/2002JA009625
Borovsky JE, Valdivia JA (2018) The Earth’s magnetosphere: a system science overview and assessment. Surv Geophys 39(5):817–859
Borovsky JE, Elphic RC, Funsten HO, Thomsen MF (1997) The Earth’s plasma sheet as a laboratory for fluid turbulence in high-\(\beta \) MHD. J Plasma Phys 57:1–34
Boynton RJ, Balikhin MA, Billings SA, Wei HL, Ganushkina N (2011) Using the NARMAX OLS-ERR algorithm to obtain the most influential coupling functions that affect the evolution of the magnetosphere. J Geophys Res 116:A05218. https://doi.org/10.1029/2010JA015505
Boynton RJ, Balikhin MA, Billings SA, Reeves GD, Ganushkina N, Gedalin M et al. (2013) The analysis of electron fluxes at geosynchronous orbit employing a NARMAX approach. J Geophys Res Space Phys 118:1500–1513. https://doi.org/10.1002/jgra.50192
Boynton RJ, Balikhin MA, Billings SA (2015) Online NARMAX model for electron fluxes at GEO. Ann Geophys 33:405–411. https://doi.org/10.5194/angeo-33-405-2015
Boynton RJ, Aryan H, Walker SN, Krasnoselskikh V, Balikhin MA (2018b) The influence of solar wind and geomagnetic indices on lower band chorus emissions in the inner magnetosphere. J Geophys Res Space Phys 123:9022–9034. https://doi.org/10.1029/2018JA025704
Boynton R, Balikhin M, Wei H-L, Lang Z-Q (2018a) Applications of NARMAX in space weather. In: Machine learning techniques for space weather. Elsevier, Amsterdam, pp 203–237
Brillouin L (2013) Science and information theory. Courier Corporation, Chelmsford
Broomhead DS, King GP (1986) Extracting qualitative dynamics from experimental data. Physica D 20(2–3):217
Burton RK, McPherron RL, Russell CT (1975) An empirical relationship between interplanetary conditions and Dst. J Geophys Res 80:4204–4214
Camporeale E (2015) Resonant and nonresonant whistlers-particle interaction in the radiation belts. Geophys Res Lett 42:3114–3121. https://doi.org/10.1002/2015GL063874
Camporeale E, Zimbardo G (2015) Wave-particle interactions with parallel whistler waves: nonlinear and time-dependent effects revealed by particle-in-cell simulations. Phys Plasmas 22:092104. https://doi.org/10.1063/1.4929853
Cayton TE, Tuszewski M (2005) Improved electron fluxes from the synchronous orbit particle analyzer. Space Weather 3:S11B05. https://doi.org/10.1029/2005SW000150
Chang T (1992) Low-dimensional behavior and symmetry breaking of stochastic systems near criticality-can these effects be observed in space and in the laboratory? IEEE Trans Plasma Sci 20(6):691–694. https://doi.org/10.1109/27.199515
Chang T (1999) Self-organized criticality, multifractal spectra, sporadic localized reconnections and intermittent turbulence. Phys Plasmas 6:4137
Chang T (1998) Sporadic localized reconnections and multiscale intermittent turbulence in the magnetotail. In: Horvitz JL et al. (eds) Geospace mass and energy flow. Geophys monograph, vol 104, p 193
Chang T, Tam SWY, Wu C-C (2006) Complexity in space plasmas – a brief review. Space Sci Rev 122:281–291. https://doi.org/10.1007/s11214-006-5957-4
Chapman S, Ferraro VCA (1931) A new theory of magnetic storms, part 1, the initial phase. Terr Magn Atmos Electr 36:171–186
Chapman SC, Watkins NW, Dendy R, Helander P, Rowlands G (1998) A simple avalanche model as an analogue for magnetospheric activity. Geophys Res Lett 25:2397. https://doi.org/10.1029/98GL51700
Chapman SC, Rowlands G, Watkins NW (2009) Macroscopic control parameter for avalanche models for bursty transport. Phys Plasmas 16:012303. https://doi.org/10.1063/1.3057392
Chapman SC, Watkins NW, Tindale E (2018) Reproducible aspects of the climate of space weather over the last five solar cycles. Space Weather. https://doi.org/10.1029/2018SW001884
Chapman SC, McIntosh SW, Leamon RJ, Watkins NW (2020) Quantifying the solar cycle modulation of extreme space weather. Geophys Res Lett. https://doi.org/10.1029/2020GL087795
Chatfield C (2016) The analysis of time series – an introduction, 6th edn. Chapman and Hall/CRC, London
Chen J, Palmadesso PJ (1986) Chaos and nonlinear dynamics of single-particle orbits in a magnetotail-like magnetic field. J Geophys Res Space Phys 91(A2):1499–1508
Chen W, Wang Z, Xie H, Yu W (2007) Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans Neural Syst Rehabil Eng 15:266–272
Chen W, Zhuang J, Yu W, Wang Z (2009) Measuring complexity using FuzzyEn, ApEn, and SampEn. Med Eng Phys 31:61–68
Claudepierre SG, Hudson MK, Lotko W, Lyon JG, Denton RE (2010) Solar wind driving of magnetospheric ULF waves: field line resonances driven by dynamic pressure fluctuations. J Geophys Res 115:A11202. https://doi.org/10.1029/2010JA015399
Colebrook JM (1978) Continuous plankton records-zooplankton and environment, northeast Atlantic and North-Sea, 1948-1975. Oceanol Acta 1:9
Consolini G (2002) Self-organized criticality: a new paradigm for the magnetotail dynamics. Fractals 10(3):275–283
Consolini G, Marcucci MF, Candidi M (1996) Multifractal structure of auroral electrojet index data. Phys Rev Lett 76(21):4082–4085
Consolini G (1997) Sandpile cellular automata and the magnetospheric dynamics, cosmic physics in the year 2000. In: Aiello S et al. (eds) Proceedings of 8th GIFCO conference. SIF, Bologna, p 123
Consolini G, De Michelis P, Tozzi R (2008) On the Earth’s magnetospheric dynamics: nonequilibrium evolution and the fluctuation theorem. J Geophys Res Space Phys 113(A8):A08222
Consolini G, Tozzi R, De Michelis P (2009) Michelis, complexity in the sunspot cycle. Astron Astrophys 506:1381–1391. https://doi.org/10.1051/0004-6361/200811074
Consolini G, Alberti T, Yordanova E, Marcucci MF, Echim M (2017) A Hilbert-Huang transform approach to space plasma turbulence at kinetic scales. J Phys Conf Ser 900:12003
Consolini G, Tozzi R, De Michelis P, Coco I, Giannattasio F, Pezzopane M, Marcucci MF, Balasis G (2021) High-latitude polar pattern of ionospheric electron density: scaling features and IMF dependence. J Atmos Sol-Terr Phys 217:105531. https://doi.org/10.1016/j.jastp.2020.105531
Contopoulos G (2002) Order and chaos in dynamical astronomy. Astronomy and astrophysics library. vol 21. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-04917-4
Coroniti FV, Eviatar A (1977) Magnetic field reconnection in a collisionless plasma. Astrophys J Suppl Ser 33:189
Costello KA (1997) Moving the Rice MSFM into a real-time forecast mode using solar wind driven forecast models. PhD dissertation, Rice Univ, Houston, Texas
Cressie N, Read TR (1984) Multinomial goodness-of-fit tests. J R Stat Soc, Ser B, Methodol 46(3):440–464
Crosson IJ, Binder PM (2009) Chaos-based forecast of sunspot cycle 24. J Geophys Res Space Phys 114(A1):A01108
Daglis IA, Thorne RM, Baumjohann W, Orsini S (1999) The terrestrial ring current: origin, formation, and decay. Rev Geophys 37(4):407–438
Daglis IA, Kozyra JU, Kamide Y, Vassiliadis D, Sharma AS, Liemohn MW, Gonzalez WD, Tsurutani BT, Lu G (2003) Intense space storms: critical issues and open disputes. J Geophys Res 108(A5):1208. https://doi.org/10.1029/2002JA009722
Daglis IA, Tsurutani BT, Gonzalez WD, Kozyra JU, Orsini S, Cladis J, Kamide Y, Henderson MG, Vassiliadis D (2007) Key features of intense geospace storms—a comparative study of a solar maximum and solar minimum storm. Planet Space Sci 55:32–55
Darbellay GA, Vajda I (1999) Estimation of the information by an adaptive partitioning of the observations space. IEEE Trans Inf Theory 45:1315–1321
Daróczy Z (1970) Generalized information functions. Inf Control 16(1):36–51
De Michelis P, Consolini G (2015) On the local Hurst exponent of geomagnetic field fluctuations: spatial distribution for different geomagnetic activity levels. J Geophys Res Space Phys 120:2691–2701. https://doi.org/10.1002/2014JA020685
De Michelis P, Consolini G, Materassi M, Tozzi R (2011) An information theory approach to the storm-substorm relationship. J Geophys Res 116:A08225. https://doi.org/10.1029/2011JA016535
De Michelis P, Consolini G, Tozzi R, Marcucci MF (2016) Observations of high-latitude geomagnetic field fluctuations during St. Patrick’s Day storm: Swarm and SuperDARN measurements. Earth Planets Space 68:105. https://doi.org/10.1186/s40623-016-0476-3
De Michelis P, Consolini G, Tozzi R, Marcucci MF (2017a) Scaling features of high-latitude geomagnetic field fluctuations at Swarm altitude: impact of IMF orientation. J Geophys Res Space Phys 122:10,548–10,562. https://doi.org/10.1002/2017JA024156
De Michelis P, Tozzi R, Consolini G (2017b) Statistical analysis of geomagnetic field intensity differences between ASM and VFM instruments onboard Swarm constellation. Earth Planets Space 69:24. https://doi.org/10.1186/s40623-016-0583-1
De Michelis P, Pignalberi A, Consolini G, Coco I, Tozzi R, Pezzopane M, Giannattasio F, Balasis G (2020) On the 2015 St. Patrick’s storm turbulent state of the ionosphere: hints from the Swarm mission. J Geophys Res Space Phys 125:e2020JA027934. https://doi.org/10.1029/2020JA027934
De Michelis P, Consolini G, Pignalberi A, Tozzi R, Coco I, Giannattasio F, Pezzopane M, Balasis G (2021) Looking for a proxy of the ionospheric turbulence with Swarm data. Sci Rep 11:6183. https://doi.org/10.1038/s41598-021-84985-1
De Wit TD, Krasnosel’skikh VV, Dunlop M, Luhr H (1999) Identifying nonlinear wave interactions in plasmas using two-point measurements: a case study of short large amplitude magnetic structures (SLAMS). J Geophys Res 104:17079–17090
Dessler AJ, Parker EN (1959) Hydromagnetic theory of geomagnetic storms. J Geophys Res 64:2339–2352
Ditlevsen PD (1999) Observation of a-stable noise induced millen-nial climate changes from an ice-core record. Geophys Res Lett 26:1441–1444
Dods J, Chapman SC, Gjerloev JW (2015) Network analysis of geomagnetic substorms using the SuperMAG database of ground-based magnetometer stations. J Geophys Res Space Phys 120:7774–7784. https://doi.org/10.1002/2015JA021456
Dods J, Chapman SC, Gjerloev JW (2017) Characterizing the ionospheric current pattern response to southward and northward IMF turnings with dynamical SuperMAG correlation networks. J Geophys Res Space Phys 122:1883–1902. https://doi.org/10.1002/2016JA023686
Donges JF, Heitzig J, Donner RV, Kurths J (2012) Analytical framework for recurrence-network analysis of time series. Phys Rev E 85:046105
Donner RV, Balasis G (2013) Correlation-based characterisation of time-varying dynamical complexity in the Earth’s magnetosphere. Nonlinear Process Geophys 20:965–975. https://doi.org/10.5194/npg-20-965-2013
Donner RV, Heitzig J, Donges JF, Zou Y, Marwan N, Kurths J (2011b) The geometry of chaotic dynamics – a complex network perspective. Eur Phys J B 84:653–672
Donner RV, Small M, Donges JF, Marwan N, Zou Y, Xiang R, Kurths J (2011a) Recurrence-based time series analysis by means of complex network methods. Int J Bifurc Chaos 21:1019–1046
Donner RV, Stolbova V, Balasis G, Donges JF, Georgiou M, Potirakis SM, Kurths J (2018) Temporal organization of magnetospheric fluctuations unveiled by recurrence patterns in the Dst index. Chaos 28:085716. https://doi.org/10.1063/1.5024792
Donner RV, Balasis G, Stolbova V, Georgiou M, Wiedermann M, Kurths J (2019) Recurrence based quantification of dynamical complexity in the Earth’s magnetosphere at geospace storm timescales. J Geophys Res Space Phys 124:90–108. https://doi.org/10.1029/2018JA025318
Dungey JW (1961) Interplanetary magnetic field and the auroral zones. Phys Rev Lett 6:47
Ebeling W, Nicolis G (1992) Word frequency and entropy of symbolic sequences: a dynamical perspective. Chaos Solitons Fractals 2(6):635–650. https://doi.org/10.1016/0960-0779(92)90058-U
Echer E, Gonzalez WD, Tsurutani BT, Gonzalez ALC (2008) Interplanetary conditions causing intense geomagnetic storms (\(\mathrm{Dst} \leq -100\text{ nT}\)) during solar cycle 23 (1996-2006). J Geophys Res 113:A05221. https://doi.org/10.1029/2007JA012744
Eckmann J-P, Oliffson Kamphorst S, Ruelle D (1987) Recurrence plots of dynamical systems. Europhys Lett 4:973–979
Einstein A (1905) Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann Phys 322:549–560
El-Taher A, Thabet A (2021) The interconnection and phase asynchrony between the geomagnetic indices’ periodicities: a study based on the interplanetary magnetic field polarities 1967–2018 utilizing a cross wavelet analysis. Adv Space Res 67:3213
Elkington SR, Hudson MK, Chan AA (1999) Acceleration of relativistic electrons via drift-resonant interaction with toroidal-mode Pc-5 ULF oscillations. Geophys Res Lett 26:3273
Elsner JB, Tsonis AA (1996) Singular spectrum analysis. Springer, Boston. https://doi.org/10.1007/978-1-4757-2514-8
Engebretson M, Glassmeier K-H, Stellmacher M, Hughes WJ, Lühr H (1998) The dependence of high-latitude PcS wave power on solar wind velocity and on the phase of high-speed solar wind streams. J Geophys Res 103(A11):26271–26283. https://doi.org/10.1029/97JA03143
Farmer JD, Sidorowich JJ (1987) Predicting chaotic time series. Phys Rev Lett 59(8):845–848. https://doi.org/10.1103/PhysRevLett.59.845
Fisher RA (1925) Theory of statistical estimation. Math Proc Camb Philos Soc 22(5):700–725
Flandrin P, Rilling G, Goncalves P (2004) Empirical mode decomposition as a filter bank. IEEE Signal Process Lett 11:112–114
Fraedrich K (1986) Estimating the dimensions of weather and climate attractors. J Atmos Sci 43(5):419–432
Fraser AM, Swinney HL (1986) Independent coordinates for strange attractors from mutual information. Phys Rev A 33(2):1134
Fukata M, Taguchi S, Okuzawa T, Obara T (2002) Neural network prediction of relativistic electrons at geosynchronous orbit during the storm recovery phase: effects of recurring substorms. Ann Geophys 20:947–951
Galeev AA, Coroniti FV, Ashour-Abdalla M (1978) Explosive tearing mode reconnection in the magnetospheric tail. Geophys Res Lett 5(8):707–710
Ganushkina NY, Pulkkinen T, Fritz T (2005) Role of substorm-associated impulsive electric fields in the ring current development during storms. Ann Geophys 23:579–591
Gerhardus A, Runge J (2020) High-recall causal discovery for autocorrelated time series with latent confounders. Adv Neural Inf Process Syst 2020:33
Ghil M, Vautard R (1991) Interdecadal oscillations and the warming trend in global temperature time series. Nature 350:324
Ghil M, Allen MR, Dettinger MD, Ide K, Kondrashov D, Mann ME, Robertson AW, Saunders A, Tian Y, Varadi F, Yiou P (2002) Advanced spectral methods for climatic time series. Rev Geophys 40(1):3
Giagkiozis I, Walker SN, Balikhin MA (2011) Dynamics of ion sound waves in the front of the terrestrial bow shock. Ann Geophys 29:805–811
Gjerloev JW (2012) The SuperMAG data processing technique. J Geophys Res 117:A09213. https://doi.org/10.1029/2012JA017683
Golyandina N, Nekrutkin V, Zhigljavsky AA (2001) Analysis of time series structure: SSA and related techniques. CRC Press, Boca Raton
Gonzalez WD, Tsurutani BT (1987) Criteria of interplanetary parameters causing intense magnetic storms (\(\mathrm{Dst} < -100\text{ nT}\)). Planet Space Sci 35:1101–1109
Gonzalez WD, Tsurutani BT, Gonzalez ALC, Smith EJ, Tang F, Akasofu S-I (1989) Solar wind-magnetosphere coupling during intense magnetic storms (1978-1979). J Geophys Res 94(A7):8835–8851
Gonzalez WD, Joselyn JA, Kamide Y, Kroehl HW, Rostoker G, Tsurutani BT, Vasyliunas VM (1994) What is a geomagnetic storm. J Geophys Res 99(A4):5771–5792
Granger CW (1969) Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37:424–438
Grassberger P (1983) Generalized dimensions of strange attractors. Phys Lett A 97:227–230
Grassberger P (1985) Generalizations of the Hausdorff dimension of fractal measures. Phys Lett A 107:101–105
Grassberger P (1986) Do climatic attractors exist? Nature 323(6089):609–612
Hajra R, Tsurutani BT (2018) Interplanetary shocks inducing magnetospheric supersubstorms (\(\mathrm{SML} < -2500\text{ nT}\)): unusual auroral morphologies and energy flow. Astrophys J 858:123
Hajra R, Echer E, Tsurutani BT, Gonzalez WD (2013) Solar cycle dependence of high-intensity long-duration continuous AE activity (HILDCAA) events, relativistic electron predictors? J Geophys Res Space Phys 118:5626–5638. https://doi.org/10.1002/jgra.50530
Hajra R, Tsurutani BT, Echer E, Gonzalez WD, Santolik O (2015) Relativistic (\(\mathrm{E} > 0.6\), > 2.0, and > 4.0 MeV) electron acceleration at geosynchronous orbit during high-intensity, long-duration, continuous, AE activity (HILDCAA) events. Astrophys J 799:39. https://doi.org/10.1088/0004-637X/799/1/39
Hajra R, Tsurutani BT, Echer E, Gonzalez WD, Gjerloev JW (2016) Supersubstorms (\(\mathrm{SML} < -2500\text{ nT}\)): magnetic storm and solar cycle dependences. J Geophys Res Space Phys 121:7805–7816. https://doi.org/10.1002/2015JA021835
Hassani H, Zhigljavsky A (2009) Singular spectrum analysis: methodology and application to economics data. J Syst Sci Complex 22(3):372
Hasselmann K (1976) Stochastic climate models part I. Theory. Tellus 28(6):473–485
Havrda J, Charvát F (1967) Quantification method of classification processes. Concept of structural \(\alpha \)-entropy. Kybernetika 3(1):30–35
Heppner JP (1955) Note on the occurrence of world-wide SSCs during the onset of negative bays at College, Alaska. J Geophys Res 60:29
Higuchi T (1988) Approach to an irregular time series on the basis of the fractal theory. Physica D 31:277–283
Hnat B, Chapman SC, Rowlands G (2004) Scaling, asymmetry and Fokker Planck models of the fast and slow solar wind as seen by WIND. Phys Plasmas 11:1326. https://doi.org/10.1063/1.1667500
Hnat B, Chapman SC, Rowlands G (2005) Scaling and a Fokker-Planck model for fluctuations in geomagnetic indices and comparison with solar wind epsilon as seen by WIND and ACE. J Geophys Res 110:A08206. https://doi.org/10.1029/2004JA010824
Hones EW Jr, Birn J, Baker DN, Bame SJ, Feldman WC, McComas DJ, Zwickl RD, Slavin JA, Smith EJ, Tsurutani BT (1984) Detailed examination of a plasmoid in the distant magnetotail with ISEE 3. Geophys Res Lett 11(10):1046–1049
Horne RB, Thorne RM, Glauert SA, Albert JM, Meredith NP, Anderson RR (2005) Timescale for radiation belt electron acceleration by whistler mode chorus waves. J Geophys Res 110(A3):A03225. https://doi.org/10.1029/2004JA010811
Horne RB, Thorne RM, Glauert SA, Meredith NP, Pokhotelov D, Santolík O (2007) Electron acceleration in the Van Allen radiation belts by fast magnetosonic waves. Geophys Res Lett 34:L17107. https://doi.org/10.1029/2007GL030267
Huang NE, Wu Z (2008) A review on Hilbert-Huang transform: method and its applications to geophysical studies. Rev Geophys 46:RG2006. https://doi.org/10.1029/2007RG000228
Huang NE, Shen Z, Long SR (1998) The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc R Soc Lond A 454:903–995. https://doi.org/10.1098/rspa.1998.0193
Huang NE, Shen Z, Long RS (1999) A new view of nonlinear water waves – the Hilbert spectrum. Annu Rev Fluid Mech 31:417–457. https://doi.org/10.1146/annurev.fluid.31.1.417
Huba JD, Gladd NT, Papadopoulos K (1977) The lower-hybrid-drift instability as a source of anomalous resistivity for magnetic field line reconnection. Geophys Res Lett 4(3):125–129
Hundhausen AJ, Bame SJ, Asbridge JR, Sydoriak SJ (1970) Solar wind proton properties: Vela 3 observations from July 1965 to June 1967. J Geophys Res 75(25):4643–4657. https://doi.org/10.1029/JA075i025p04643
Hush P, Chapman SC, Dunlop MW, Watkins NW (2015) Robust statistical properties of the size of large burst events in AE. Geophys Res Lett 42:9197–9202. https://doi.org/10.1002/2015GL066277
Ichimaru S (1973) Basic principles of plasma physics, 1st edn. Benjamin, Elmsford.
Iyemori T (1990) Storm-time magnetospheric currents inferred from mid-latitude geomagnetic field variations. J Geomagn Geoelectr 42(11):1249–1265. https://doi.org/10.5636/jgg.42.1249
Jensen H (1998) Self-organized criticality: emergent complex behavior in physical and biological systems. Cambridge lecture notes in physics. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511622717
Johnson JR, Wing S (2005) A solar cycle dependence of nonlinearity in magnetospheric activity. J Geophys Res 110:A04211. https://doi.org/10.1029/2004JA010638
Johnson JR, Wing S (2014) External versus internal triggering of substorms: an information-theoretical approach. Geophys Res Lett 41:5748–5754. https://doi.org/10.1002/2014GL060928
Johnson JR, Wing S, Delamere PA (2014) Kelvin Helmholtz instability in planetary magnetospheres. Space Sci Rev 184:1–31. https://doi.org/10.1007/s11214-014-0085-z
Johnson JR, Wing S, Camporeale E (2018) Transfer entropy and cumulant-based cost as measures of nonlinear causal relationships in space plasmas: applications to Dst. Ann Geophys 36:945–952. https://doi.org/10.5194/angeo-36-945-2018
Jordanova VK, Farrugia CJ, Janoo L, Quinn JM, Torbert RB, Ogilvie KW, Belian RD (1998) October 1995 magnetic cloud and accompanying storm activity: ring current evolution. J Geophys Res 103:79–92. https://doi.org/10.1029/97JA02367
Joselyn JA, Tsurutani BT (1990) Geomagnetic impulses and storm sudden commencements. Eos Trans AGU 71:1808–1809
Joselyn J, Lundstedt H, Trollinger J (eds) (1994) Proceedings of the international workshop on artificial intelligence applications in solar terrestrial physics, Lund, Sweden, 22–24 September 1993. National Oceanic and Atmospheric Administration, Space Environment Laboratory, Boulder
Kadanoff LP (2000) Statistical physics: statics, dynamics and renormalization. World Scientific, Singapore
Kamide Y, Perreault PD, Akasofu S-I, Winningham JD (1977) Dependence of substorm occurrence probability on the interplanetary magnetic field and on the size of the aurora oval. J Geophys Res 82(35):5521–5528
Kamide Y, Baumjohann W, Daglis IA, Gonzalez WD, Grande M, Joselyn JA, McPherron RL, Phillips JL, Reeves EGD, Rostoker G, Sharma AS, Singer HJ, Tsurutani BT, Vasyliunas VM (1998) Current understanding of magnetic storms: storm-substorm relationships. J Geophys Res 103:17,705
Kan JR, Lee LC (1979) Energy coupling function and solar wind-magnetosphere dynamo. Geophys Res Lett 6:577–580
Kardar M (2007) Statistical physics of particles. Cambridge University Press, Cambridge
Katsavrias C, Papadimitriou C, Aminalragia-Giamini S, Daglis IA, Sandberg I, Jiggens P (2021) On the semi-annual variation of relativistic electrons in the outer radiation belt. Ann Geophys 39:413
Katsavrias C, Papadimitriou C, Hillaris A, Balasis G (2022) Application of wavelet methods in the investigation of geospace disturbances: a review and an evaluation of the approach for quantifying wavelet power. Atmosphere 13:499
Katz MJ (1988) Fractals and the analysis of waveforms. Comput Biol Med 18:145–156
Kellerman AC, Shprits YY (2012) On the influence of solar wind conditions on thouter-electron radiation belt. J Geophys Res 117:A05217. https://doi.org/10.1029/2011JA017253
Kennel CF, Edmiston JP, Hada T (1985) A quarter century of collisionless shock research. In: Stone RC, Tsurutani BT (eds) Collisionless shocks in the heliosphere: a tutorial review, vol 34. Amer. Geophys. Un. Press, Washington, p 1
Kepko L, Spence HE (2003) Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J Geophys Res 108:1257. https://doi.org/10.1029/2002JA009676
Keppenne CL, Ghil M (1992) Adaptive filtering and prediction of the Southern Oscillation index. J Geophys Res, Atmos 97(D18):20449
Kissinger J, McPherron RL, Hsu T-S, Angelopoulos V (2011) Steady magnetospheric convection and stream interfaces: relationship over a solar cycle. J Geophys Res 116:A00I19. https://doi.org/10.1029/2010JA015763
Kiyani K, Chapman SC, Watkins NW (2009) Pseudo-nonstationarity in the scaling exponents of finite interval time series. Phys Rev E 79:036109. https://doi.org/10.1103/PhysRevE.79.036109
Kiyani K, Chapman SC, Sahraoui F, Hnat B, Fauvarque O, Khotyaintsev YV (2013) Enhanced magnetic compressibility and isotropic scale-invariance at sub-ion Larmor scales in solar wind turbulence. Astrophys J 763:10. https://doi.org/10.1088/0004-637X/763/1/10
Klimas AJ, Vassiliadis D, Baker DN, Roberts DA (1996) The organized nonlinear dynamics of the magnetosphere. J Geophys Res 101:13089–13113
Klimas AJ, Vassiliadis D, Baker DN (1997) Data-derived analogues of the magnetospheric dynamics. J Geophys Res 102(26):993
Klimas AJ, Vassiliadis D, Baker DN (1998) Dst index prediction using data-derived analogues of the magnetospheric dynamics. J Geophys Res 103:20,435
Klimas AJ, Valdivia JA, Vassiliadis DV, Baker DN, Hesse M, Takalo J (2000) Self-organized criticality in the substorm phenomenon and its relation to localized reconnection in the magnetospheric plasma sheet. J Geophys Res 105:18765
Klimas AJ, Uritsky VM, Vassiliadis D, Baker DN (2005) Simulation study of SOC dynamics in driven current-sheet models. In: Burton W et al. (eds) Nonequilibrium phenomena in plasmas. Astrophysics and space science library, vol 321. Springer, Dordrecht, pp 71–89. https://doi.org/10.1007/1-4020-3109-2_4
Kolmogorov AN (1938) On the analytic methods of probability theory. Usp Mat Nauk 5:5–41
Korotova GI, Sibeck DG (1995) A case study of transient event motion in the magnetosphere and in the ionosphere. J Geophys Res 100(A1):35–46. https://doi.org/10.1029/94JA02296
Kozyra JU, Jordanova VK, Horne RB, Thorne RM (1997) Modeling of the contribution of electromagnetic ion cyclotron (EMIC) waves to stormtime ring current erosion. In: Tsurutani BT et al. (eds) Magnetic storms. Geophys Monogr Ser, vol 98. AGU, Washington, p 187
Kozyra JU, Liemohn MW, Clauer CR, Ridley AJ, Thomsen MF, Borovsky JE, Roeder JL, Jordanova VK, Gonzalez WD (2002) Multistep Dst development and ring current composition changes during the 4–6 June 1991 magnetic storm. J Geophys Res 107(A8):1224. https://doi.org/10.1029/2001JA000023
Krieger AS, Timothy AF, Roelof EC (1973) A coronal hole and its identification as the source of a high velocity solar wind stream. Sol Phys 29:505–525. https://doi.org/10.1007/BF00150828
Kullback S (1997) Information theory and statistics. Courier Corporation, Chelmsford
Kunagu P, Balasis G, Lesur V, Chandrasekhar E, Papadimitriou C (2013) Wavelet characterization of external magnetic sources as observed by CHAMP satellite: evidence for unmodelled signals in geomagnetic field models. Geophys J Int 192:946
Kwasniok F, Lohmann G (2009) Deriving dynamical models from paleoclimatic records: application to glacial millennial-scale climate variability. Phys Rev E 80:066104. https://doi.org/10.1103/PhysRevE.80.066104
Lakhina GS, Tsurutani BT (1998) Explosive energy release by disruption of current sheets. Phys Scr T 74:67–70
Langevin P (1908) Sur la théorie du mouvement brownien. C R Acad Sci 146:530–533
Leontaritis IJ, Billings SA (1985a) Input-output parametric models for non-linear systems, part I: deterministic non-linear systems. Int J Control 41(2):303–328
Leontaritis IJ, Billings SA (1985b) Input-output parametric models for non-linear systems, part II: stochastic nonlinear systems. Int J Control 41(2):329–344
Lewis ZV (1991) On the apparent randomness of substorm onset. Geophys Res Lett 18:1627
Li W (1990) Mutual information functions versus correlation functions. J Stat Phys 60:823–837
Li X (2004) Variations of 0.7-6.0 MeV electrons at geosynchronous orbit as a function of solar wind. Space Weather 2:S03006. https://doi.org/10.1029/2003SW000017
Li X, Temerin M, Baker D, Reeves G, Larson D (2001) Quantitative prediction of radiation belt electrons at geostationary orbit based on solar wind measurements. Geophys Res Lett 28(9):1887–1890
Li X, Baker DN, Temerin M, Reeves G, Friedel R, Shen C (2005) Energetic electrons, 50 keV to 6 MeV, at geosynchronous orbit: their responses to solar wind variations. Space Weather 3:S04001. https://doi.org/10.1029/2004SW000105
Ling AG, Ginet GP, Hilmer RV, Perry KL (2010) A neural-network-based geosynchronous relativistic electron flux forecasting model. Space Weather 8:S09003. https://doi.org/10.1029/2010SW000576
Liu L, Zou S, Yao Y, Wang Z (2020) Forecasting global ionospheric TEC using deep learning approach. Space Weather 18:e2020SW002501. https://doi.org/10.1029/2020SW002501
Livadiotis G (2018) Derivation of the entropic formula for the statistical mechanics of space plasmas. Nonlinear Process Geophys 25(1):77–88
Livina VN, Kwasniok F, Lenton TM (2010) Potential analysis reveals changing number of climate states during the last 60 kyr. Clim Past 6:77–82
Lorenz EN (1991) Dimension of weather and climate attractors. Nature 353(6341):241–244
Lou YQ, Wang YM, Fan Z, Wang S, Wang JX (2003) Periodicities in solar coronal mass ejections. Mon Not R Astron Soc 345:809818
Lucarini V, Faranda D, Wouters J (2012) Universal behaviour of extreme value statistics for selected observables of dynamical systems. J Stat Phys 147:63–73
Lui ATY, Chapman SC, Liou K, Newell PT, Meng C-I, Brittnacher MJ, Parks GK (2000) Is the dynamic magnetosphere an avalanching system? Geophys Res Lett 27:911. https://doi.org/10.1029/1999GL010752
Lyatsky W, Khazanov GV (2008) Effect of solar wind density on relativistic electrons at geosynchronous orbit. Geophys Res Lett 35:L03109. https://doi.org/10.1029/2007GL032524
Maggiolo R, Hamrin M, De Keyser J, Pitkänen T, Cessateur G, Gunell H, Maes L (2017) The delayed time response of geomagnetic activity to the solar wind. J Geophys Res Space Phys 122(11):11–109
Manshour P, Balasis G, Consolini G, Papadimitriou C, Paluš M (2021) Causality and information transfer between the solar wind and the magnetosphere–ionosphere system. Entropy 23(4):390
Mao X (2007) Stochastic differential equations and applications. Elsevier, Amsterdam
March TK, Chapman SC, Dendy RO (2005) Mutual information between geomagnetic indices and the solar wind as seen by WIND: implications for propagation time estimates. Geophys Res Lett 32:L04101. https://doi.org/10.1029/2004GL021677
Martin MT, Pennini F, Plastino A (1999) Fisher’s information and the analysis of complex signals. Phys Lett A 256:173–180
Marwan N, Romano MC, Thiel M, Kurths J (2007) Recurrence plots for the analysis of information theory. Phys Rep 438:237–329
Materassi M, Ciraolo L, Consolini G, Smith N (2011) Predictive space weather: an information theory approach. Adv Space Res 47:877–885. https://doi.org/10.1016/j.asr.2010.10.026
Mathie RA, Mann IR (2000) A correlation between extended intervals of ULF wave power and storm-time geosynchronous relativistic electron flux enhancements. Geophys Res Lett 27:3261–3264. https://doi.org/10.1029/2000GL003822
Mathie RA, Mann IR (2001) On the solar wind control of Pc5 ULF pulsation power at mid-latitudes: implications for MeV electron acceleration in the outer radiation belt. J Geophys Res 106(A12):29783–29796. https://doi.org/10.1029/2001JA000002
McComas DJ et al. (2002) Ulysses second fast latitude scan; complexity near solar maximum and the reformation of polar coronal holes. Geophys Res Lett 29(9):1290. https://doi.org/10.1029/2001GL014164
McGranaghan RM, Mannucci AJ, Verkhoglyadova O, Malik N (2017) Finding multiscale connectivity in our geospace observational system: network analysis of total electron content. J Geophys Res Space Phys 122:7683–7697. https://doi.org/10.1002/2017JA024202
Meier MM, Belian RD, Cayton TE, Christensen RA, Garcia B, Grace KM, Ingraham JC, Laros JG, Reeves GD (1996) The energy spectrometer for particles (ESP): instrument description and orbital performance. AIP Conf Proc 383:203–210
Mendes O Jr, Domingues MO, Da Costa AM, De Gonzalez ALC (2005) Wavelet analysis applied to magnetograms: singularity detections related to geomagnetic storms. J Atmos Sol-Terr Phys 67:1827
Miyoshi Y, Kataoka R (2008) Flux enhancement of the outer radiation belt electrons after the arrival of stream interaction regions. J Geophys Res 113:A03S09. https://doi.org/10.1029/2007JA012506
Nagai A (1993) Prediction of magnetospheric parameters using artificial neural networks. PhD thesis, Rice University
Newell PT, Sotirelis T, Liou K, Meng C-I, Rich FJ (2007) A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables. J Geophys Res 112:A01206. https://doi.org/10.1029/2006JA012015
Newell PT, Liou K, Gjerloev JW, Sotirelis T, Wing S, Mitchell EJ (2016) Substorm probabilities are best predicted from solar wind speed. J Atmos Sol-Terr Phys 146:28–37. https://doi.org/10.1016/j.jastp.2016.04.019
Nicolis C, Nicolis G (1984) Is there a climatic attractor? Nature 311(5986):529–532
Nishida A (1968) Coherence of geomagnetic DP2 fluctuations with interplanetary magnetic variations. J Geophys Res Space Phys 73(17):5549–5559
Noble PL, Wheatland MS (2012) A Bayesian approach to forecasting solar cycles using a Fokker–Planck equation. Sol Phys 276:363–381. https://doi.org/10.1007/s11207-011-9884-5
Omura Y, Furuya N, Summers D (2007) Relativistic turning acceleration of resonant electrons by coherent whistler mode waves in a dipole magnetic field. J Geophys Res 112:A06236. https://doi.org/10.1029/2006JA012243
Onsager TG, Green JC, Reeves GD, Singer HJ (2007) Solar wind and magnetospheric conditions leading to the abrupt loss of outer radiation belt electrons. J Geophys Res 112:A01202. https://doi.org/10.1029/2006JA011708
Orr L, Chapman SC, Gjerloev JW (2019) Directed network of substorms using SuperMAG ground-based magnetometer data. Geophys Res Lett 46:6268–6278. https://doi.org/10.1029/2019GL082824
Orr L, Chapman SC, Gjerloev JW et al. (2021) Network community structure of substorms using SuperMAG magnetometers. Nat Commun 12:1842. https://doi.org/10.1038/s41467-021-22112-4
Paluš M (1996) Coarse-grained entropy rates for characterization of complex time series. Phys D, Nonlinear Phenom 93(1–2):64–77
Paluš M (1997) On entropy rates of dynamical systems and Gaussian processes. Phys Lett A 227(5–6):301–308
Paluš M (2014) Multiscale atmospheric dynamics: cross-frequency phase-amplitude coupling in the air temperature. Phys Rev Lett 112(7):078702
Paluš M, Novotná D (1994) Testing for nonlinearity in weather records. Phys Lett A 193(1):67–74
Paluš M, Novotna D (2004) Enhanced Monte Carlo singular system analysis and detection of period 7.8 years oscillatory modes in the monthly NAO index and temperature records. Nonlinear Process Geophys 11:721
Paluš M, Novotná D (2008) Detecting oscillations hidden in noise: common cycles in atmospheric, geomagnetic and solar data. In: Donner RV, Barbosa SM (eds) Nonlinear time series analysis in the geosciences. Lecture notes in Earth sciences, vol 112. Springer, Berlin, Heidelberg, pp 327–353. https://doi.org/10.1007/978-3-540-78938-3_15
Paluš M, Novotná D (2009) Phase-coherent oscillatory modes in solar and geomagnetic activity and climate variability. J Atmos Sol-Terr Phys 71:923
Paluš M, Vejmelka M (2007) Directionality of coupling from bivariate time series: how to avoid false causalities and missed connections. Phys Rev E 75(5):056211
Paluš M, Komárek V, Hrnčíř Z, Štěrbová K (2001) Synchronization as adjustment of information rates: detection from bivariate time series. Phys Rev E 63:046211
Paluš M, Hartman D, Hlinka J, Vejmelka M (2011) Discerning connectivity from dynamics in climate networks. Nonlinear Process Geophys 18(5):751–763
Papadimitriou C, Balasis G, Boutsi AZ, Daglis IA, Giannakis O, Anastasiadis A, De Michelis P, Consolini G (2020) Dynamical complexity of the 2015 St. Patrick’s Day magnetic storm at Swarm altitudes using entropy measures. Entropy 22:574. https://doi.org/10.3390/e22050574
Paulikas GA, Blake JB (1979) Effects of the solar wind on magnetospheric dynamics: energetic electrons at the synchronous orbit. In: Quantitative modeling of magnetospheric processes. Geophys Monogr Ser, vol 21, pp 180–202. AGU, Washington
Perreault WK, Akasofu S-I (1978) A study of geomagnetic storms. Geophys J R Astron Soc 54:547–573
Pincus SM (1991) Approximate entropy as a measure of system complexity. Proc Natl Acad Sci USA 88(6):2297–2301
Prichard D, Theiler J (1995) Generalized redundancies for time series analysis. Phys D, Nonlinear Phenom 84:476–493. https://doi.org/10.1016/0167-2789(95)00041-2
Prokopenko M, Lizier JT, Price DC (2013) On thermodynamic interpretation of transfer entropy. Entropy 15(2):524–543. https://doi.org/10.3390/e15020524
Pytte T, McPherron RL, Hones EW Jr, West HI Jr (1978) Multiple-satellite studies of magnetospheric substorms: distinction between polar magnetic substorms and convection driven negative bays. J Geophys Res 83:663
Reeves GD, Morley SK, Friedel RHW, Henderson MG, Cayton TE, Cunningham G, Blake JB, Christensen RA, Thomsen D (2011) On the relationship between relativistic electron flux and solar wind velocity: Paulikas and Blake revisited. J Geophys Res 116:A02213. https://doi.org/10.1029/2010JA015735
Rényi A (1961) On measures of entropy and information. In: Proceedings of the fourth Berkeley symposium on mathematical statistics and probability, volume 1: contributions to the theory of statistics, vol 4. University of California Press, Berkeley, pp 547–562
Ribeiro HV, Jauregui M, Zunino L, Lenzi EK (2017) Characterizing time series via complexity-entropy curves. Phys Rev E 95(6):062106. https://doi.org/10.1103/PhysRevE.95.062106
Richman JS, Moorman JR (2000) Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol, Heart Circ Physiol 278(6):H2039-49
Rigler EJ, Wiltberger M, Baker DN (2007) Radiation belt electrons respond to multiple solar wind inputs. J Geophys Res 112:A06208. https://doi.org/10.1029/2006JA012181
Ritz CP, Powers EJ, Bengtson RD (1989) Experimental measurement of three-wave coupling and energy cascading. Phys Fluids B 1:153–163
Rosso OA, Larrondo HA, Martin MT, Plastino A, Fuentes MA (2007) Distinguishing noise from chaos. Phys Rev Lett 99(15):154102. https://doi.org/10.1103/PhysRevLett.99.154102
Rostoker G, Fälthammar C-G (1967) Relationship between changes in the interplanetary magnetic field and variations in the magnetic field at the Earth’s surface. J Geophys Res 72:5853–5863
Rostoker G, Skone S, Baker DN (1998) On the origin of relativistic electrons in the magnetosphere associated with some geomagnetic storms. Geophys Res Lett 25:3701–3704. https://doi.org/10.1029/98GL02801
Roux A, Perraut S, Robert P, Morane A, Pedersen A, Korth A, Kremser G, Aparicio B, Rodgers D, Pellinen R (1991) Plasma sheet instability related to the westward traveling surge. J Geophys Res 96(A10):17697–17714
Runge J (2020) Discovering contemporaneous and lagged causal relations in autocorrelated nonlinear time series datasets. In: Proceedings of the 36th conference on uncertainty in artificial intelligence, UAI 2020, Toronto, Canada, 2019. AUAI Press, Corvallis
Runge J, Petoukhov V, Donges JF, Hlinka J, Jajcay N, Vejmelka M, Hartman D, Marwan N, Paluš M, Kurths J (2015) Identifying causal gateways and mediators in complex spatio-temporal systems. Nat Commun 8:8502
Runge J, Balasis G, Daglis IA, Papadimitriou C, Donner RV (2018) Common solar wind drivers behind magnetic storm–magnetospheric substorm dependency. Sci Rep 8:1–10
Runge J, Bathiany S, Bollt E, Camps-Valls G, Coumou D, Deyle E, Glymour C, Kretschmer M, Mahecha MD, Muñoz-MarıJ, van Nes EH, Peters J, Quax R, Reichstein M, Scheffer M, Schölkopf B, Spirtes P, Sugihara G, Sun J, Zhang K, Zscheischler J (2019a) Inferring causation from time series in Earth system sciences. Nat Commun 2019(10):2553
Runge J, Nowack P, Kretschmer M, Flaxman S, Sejdinovic D (2019b) Detecting and quantifying causal associations in large nonlinear time series datasets. Sci Adv 5:eaau4996
Russell CT, Elphic RC (1978) Initial ISEE magnetometer results: magnetopause observations. Space Sci Rev 22:681–715. https://doi.org/10.1007/BF00718586
Schindler K (1975) Plasma and fields in the magnetospheric tail. Space Sci Rev 17:589–614. https://doi.org/10.1007/BF00718586
Schreiber T (2000) Measuring information transfer. Phys Rev Lett 85:461–464. https://doi.org/10.1103/PhysRevLett.85.461
Sckopke N (1966) A general relation between the energy of trapped particles and the disturbance field near the Earth. J Geophys Res 71(13):3125–3130. https://doi.org/10.1029/JZ071i13p03125
Scurry L, Russell CT (1991) Proxy studies of energy transfer to the magnetosphere. J Geophys Res 96:9541–9548
Sergeev VA, Pellinen RJ, Pulkkinen TI (1996) Steady magnetospheric convection: a review of recent results. Space Sci Rev 75:551–604. https://doi.org/10.1007/BF00833344
Shannon CE (1948) A mathematical theory of communication. Bell Syst Tech J 27(3):379–423
Sharma AS (1995) Assessing the magnetosphere’s nonlinear behaviour: its dimension is low, its predictability is high. Rev Geophys 33(supp.):645
Sharma AS, Vassiliadis DV, Papadopoulos K (1993) Reconstruction of low-dimensional magnetospheric dynamics by singular spectrum analysis. Geophys Res Lett 20:335
Sharma AS, Sitnov MI, Papadopoulos K (2001) Substorms as nonequilibrium transitions of the magnetosphere. J Atmos Sol-Terr Phys 63:1399
Sharma AS, Baker DN, Grande M, Kamide Y, Lakhina GS, McPherron RM, Reeves GD, Rostoker G, Vondrak R, Zelenyiio L (2003) The storm-substorm relationship: current understanding and outlook. In: Sharma AS, Kamide Y, Lakhina GS (eds) Disturbances in geospace: the storm-substorm relationship. American Geophysical Union, Washington. https://doi.org/10.1029/142GM01
Shaw R (1984) Dripping faucet as a model chaotic system. Aerial Press, Santa Cruz. ISBN 0-942344-05-7
Shen Y, Guo J, Liu X, Wei X, Li W (2017) One hybrid model combining singular spectrum analysis and LS + ARMA for polar motion prediction. Adv Space Res 59:513
Shin D-K, Lee D-Y, Kim K-C, Hwang J, Kim J (2016) Artificial neural network prediction model for geosynchronous electron fluxes: dependence on satellite position and particle energy. Space Weather 14:313–321. https://doi.org/10.1002/2015SW001359
Shprits YY, Thorne RM, Friedel R, Reeves GD, Fennell J, Baker DN, Kanekal SG (2006) Outward radial diffusion driven by losses at magnetopause. J Geophys Res 111:A11214. https://doi.org/10.1029/2006JA011657
Shprits YY, Subbotin DA, Meredith NP, Elkington SR (2008) Review of modeling of losses and sources of relativistic electrons in the outer radiation belt II: local acceleration and loss. J Atmos Sol-Terr Phys 70(14):1694–1713. https://doi.org/10.1016/j.jastp.2008.06.014
Simms LE, Engebretson MJ, Smith AJ, Clilverd M, Pilipenko V, Reeves GD (2015) Analysis of the effectiveness of ground-based VLF wave observations for predicting or nowcasting relativistic electron flux at geostationary orbit. J Geophys Res Space Phys 120:2052–2060. https://doi.org/10.1002/2014JA020337
Sitnov MI, Sharma AS, Papadopoulos K, Vassiliadis D, Valdivia JA, Klimas AJ, Baker DN (2000) Phase transition-like behavior of the magnetosphere during substorms. J Geophys Res 105:12955
Sitnov MI, Sharma AS, Papadopoulos K, Vassiliadis D (2001) Modeling substorm dynamics of the magnetosphere: from self-organization and self-organized criticality to non-equilibrium phase transitions. Phys Rev E 65:16116
Smith EJ (1979) Interplanetary magnetic fields. Rev Geophys Space Phys 17(4):610–623
Sonnerup B (1974) Magnetopause reconnection rate. J Geophys Res 79:1546–1549
Sornette D (2006) Critical phenomena in natural sciences: chaos, fractals, selforganization and disorder: concepts and tools, 2nd edn. Springer series in synergetics. Springer, Heidelberg. https://doi.org/10.1007/3-540-33182-4
Stringer GA, Heuten I, Salazar C, Stokes B (1996) Artificial neural network (ANN) forecasting of energetic electrons at geosynchronous orbit. In: Lemaire JF, Heynderich D, Baker DN (eds) Radiation belts: models and standards. Geophys. Monogr. Ser., vol 97. AGU, Washington, pp 291–295
Strogatz SH (2018) Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. CRC Press, Boca Raton
Stumpo M, Consolini G, Alberti T, Quattrociocchi V (2020) Measuring information coupling between the solar wind and the magnetosphere–ionosphere system. Entropy 22:276
Sturges HA (1926) The choice of a class interval. J Am Stat Assoc 21:65–66. https://doi.org/10.1080/01621459.1926.10502161
Subbotin D, Shprits Y, Ni B (2010) Three-dimensional VERB radiation belt simulations including mixed diffusion. J Geophys Res Space Phys 115(A3):A03205
Summers D, Thorne RM, Xiao F (1998) Relativistic theory of wave-particle resonant diffusion with application to electron acceleration in the magnetosphere. J Geophys Res 103(A9):20487–20500. https://doi.org/10.1029/98JA01740
Takens F (1981) Detecting strange attractors in turbulence. In: Dynamical systems and turbulence, Warwick, 1980. Springer, Berlin, pp 366–381
Tanskanen EI (2009) A comprehensive high-throughput analysis of substorms observed by IMAGE magnetometer network: years 1993–2003 examined. J Geophys Res 114:A05204. https://doi.org/10.1029/2008JA013682
Taylor M, Daglis IA, Anastasiadis A, Vassiliadis D (2011) Volterra network modeling of the nonlinear finite-impulse response of the radiation belt flux. AIP Conf Proc 1320:221–226. https://doi.org/10.1063/1.3544328
Temerin M, Li X (2006) Dst model for 1995–2002. J Geophys Res 111:A04221. https://doi.org/10.1029/2005JA011257
Thorne RM (2010) Radiation belt dynamics: the importance of wave-particle interactions. Geophys Res Lett 37:L22107. https://doi.org/10.1029/2010GL044990
Tindale E, Chapman SC (2016) Solar cycle variation of the statistical distribution of the solar wind \(\varepsilon \) parameter and its constituent variables. Geophys Res Lett 43:5563–5570. https://doi.org/10.1002/2016GL068920
Tindale E, Chapman SC, Moloney NR, Watkins NW (2018) The dependence of solar wind burst size on burst duration and its invariance across solar cycles 23 and 24. J Geophys Res Space Phys 123:7196–7210. https://doi.org/10.1029/2018JA025740
Tsallis C (1988) Possible generalization of Boltzmann-Gibbs statistics. J Stat Phys 52:479–487. https://doi.org/10.1007/BF01016429
Tsallis C (2009) Introduction to nonextensive statistical mechanics: approaching a complex world. Springer, New York. https://doi.org/10.1007/978-0-387-85359-8
Tsonis AA (2001) Probing the linearity and nonlinearity in the transitions of the atmospheric circulation. Nonlinear Process Geophys 8:341–345
Tsonis AA (1992) Chaos: from theory to applications. Springer, Boston, MA. https://doi.org/10.1007/978-1-4615-3360-3
Tsonis AA, Elsner JB (1988) The weather attractor over very short timescales. Nature 333(6173):545–547
Tsurutani BT, Gonzalez WD (1987) The cause of high intensity long-duration continuous AE activity (HILDCAAs): interplanetary Alfvén wave trains. Planet Space Sci 35:405
Tsurutani BT, Gonzalez WD (1995) The efficiency of “viscous interaction” between the solar wind and the magnetosphere during intense northward IMF events. Geophys Res Lett 22(6):663–666
Tsurutani BT, Gonzalez WD (2007) A new perspective on the relationship between substorms and magnetic storms. Adv Geosci 8:1–21
Tsurutani BT, Hajra R (2021) The interplanetary and magnetospheric causes of geomagnetically induced currents (GICs) > 10 A in the Mantsala Finland pipeline: 1999 through 2019. J Space Weather Space Clim 11:23. https://doi.org/10.1051/swsc/2021001
Tsurutani BT, Lakhina GS (2014) An extreme coronal mass ejection and consequences for the magnetosphere and Earth. Geophys Res Lett 41:287–292. https://doi.org/10.1002/2013GL058825
Tsurutani BT, Meng C-I (1972) Interplanetary magnetic field variations and substorm activity. J Geophys Res 77(16):2964–2970
Tsurutani BT, Gonzalez WD, Tang F, Akasofu S-I, Smith EJ (1988) Origin of interplanetary southward magnetic fields responsible for major magnetic storms near solar maximum (1978-1979). J Geophys Res 93(A8):8519–8531
Tsurutani BT, Sugiura M, Iyemori T, Goldstein BE, Gonzalez WD, Akasofu S-I, Smith EJ (1990) The nonlinear response of AE to the IMF BS driver: a spectral break at 5 hours. Geophys Res Lett 17(3):279–282
Tsurutani BT, Zhou X-Y, Gonzalez WD (2004) A lack of substorm expansion phases during magnetic storms induced by magnetic clouds. In: Sharma S, Kamide Y, Lakhina G (eds) Storm-substorm relationship, vol 142. Amer. Geophys. Un. Press, Washington, p 23
Tsurutani BT, Horne RB, Pickett JS, Santolik O, Schriver D, Verkhoglyadova OP (2010) Introduction to the special section on chorus: chorus and its role in space weather. J Geophys Res 115:A00F01. https://doi.org/10.1029/2010JA015870
Tsurutani BT, Horne RB, Pickett JS, Santolik O, Schriver D, Verkhoglyadova OP (2010) Introduction to the special section on Chorus: Chorus and its role in space weather. J Geophys Res 115:A00F01. https://doi.org/10.1029/2010JA015870
Turner DL, Shprits Y, Hartinger M, Angelopoulos V (2012) Explaining sudden losses of outer radiation belt electrons during geomagnetic storms. Nat Phys 8:208–212. https://doi.org/10.1038/nphys2185
Ukhorskiy AY, Sitnov MI, Sharma AS, Anderson BJ, Ohtani S, Lui ATY (2004) Data-derived forecasting model for relativistic electron intensity at geosynchronous orbit. Geophys Res Lett 31:L09806. https://doi.org/10.1029/2004GL019616
Ukhorskiy AY, Takahashi K, Anderson BJ, Korth H (2005) Impact of toroidal ULF waves on the outer radiation belt electrons. J Geophys Res 110:A10202. https://doi.org/10.1029/2005JA011017
Ukhorskiy AY, Anderson BJ, Brandt PC, Tsyganenko NA (2006) Storm time evolution of the outer radiation belt: transport and losses. J Geophys Res 111:A11S03. https://doi.org/10.1029/2006JA011690
Uritsky VM, Pudovkin MI (1998) Low frequency 1/f-like fluctuations of the AE-index as a possible manifestation of self-organized criticality in the magnetosphere. Ann Geophys 16:1580–1588. https://doi.org/10.1007/s00585-998-1580-x
Uritsky VM, Klimas AJ, Vassiliadis D, Chua D, Parks G (2002) Scale-free statistics of spatiotemporal auroral emissions as depicted by POLAR UVI images: dynamic magnetosphere is an avalanching system. J Geophys Res 107(A12):1426. https://doi.org/10.1029/2001JA000281
Vassiliadis D (2008) Response of the radiation belt electron flux to solar wind velocity: parametrization by radial distance and energy. J Atmos Sol-Terr Phys. https://doi.org/10.1016/j.jastp.2008.05.019
Vassiliadis D (2011) Stormtime dynamics of the relativistic electron flux in Earth’s radiation belts. In: Vassiliadis D, Shao X, Fung SF, Daglis IA, Huba J (eds) Modern challenges in nonlinear plasma physics. AIP conference proceedings, vol 1320. American Institute of Physics, Melville, p 227. https://doi.org/10.1063/1.3544329
Vassiliadis D (2018) SM43D-3584, modes of response of the radiation belt electron flux to interplanetary activity, AGU fall 2018 meeting, Washington, DC, December 10–14
Vassiliadis D (2019) SM41E-3292, types of radiation belt storms as modes of response to the solar wind and IMF, AGU fall 2019 meeting, San Francisco, CA, December 9–13
Vassiliadis D, Klimas AJ, Baker DN, Roberts DA (1995) A description of solar wind-magnetosphere coupling based on nonlinear filters. J Geophys Res 100(A3):3495–3512
Vassiliadis D, Klimas AJ, Weigel RS, Baker DN, Rigler EJ, Kanekal SG, Nagai T, Fung SF, Friedel RWH, Cayton TE (2003) Structure of Earth’s outer radiation belt inferred from long-term electron flux dynamics. Geophys Res Lett 30(19):2015. https://doi.org/10.1029/2003GL017328
Vassiliadis D, Fung SF, Klimas AJ (2005) Solar, interplanetary, and magnetospheric parameters for the radiation belt energetic electron flux. J Geophys Res 110:A04201. https://doi.org/10.1029/2004JA010443
Vasyliunas VM, Kan JR, Siscoe GL, Akasofu S-I (1982) Scaling relations governing magnetosphere energy transfer. Planet Space Sci 30:359–365
Vautard R, Ghil M (1989) Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Physica D 35:395
Vennerstrøm S (1999) Dayside magnetic ULF power at high latitudes: a possible long-term proxy for the solar wind velocity? J Geophys Res 104(A5):10145–10157. https://doi.org/10.1029/1999JA900015
Von Bloh W, Romano MC, Thiel M (2005) Long-term predictability of mean daily temperature data. Nonlinear Process Geophys 12(4):471–479
Wang X, Cheng Y, Wu S, Zhang K (2016) An enhanced singular spectrum analysis method for constructing nonsecular model of GPS site movement. J Geophys Res, Solid Earth 121:2193
Watkins NW, Chapman SC, Rosenberg S (2009a) Comment on “Coexistence of self-organized criticality and intermittent turbulence in the solar corona”. Phys Rev Lett 103:039501. https://doi.org/10.1103/PhysRevLett.103.039501
Watkins NW, Credgington D, Sanchez R, Chapman SC (2009b) Linear fractional stable motion: a new kinetic equation and applications to modelling the scaling of intermittent bursts. Phys Rev E 79:041124
Watkins NW, Pruessner G, Chapman SC, Crosby NB, Jensen HJ (2015) 25 years of SOC: concepts and controversies. Space Sci Rev 198:3–44. https://doi.org/10.1007/s11214-015-0155-x
Wei HL, Billings SA, Balikhin M (2004) Analysis of the geomagnetic activity of the Dst index and self-affine fractals using wavelet transforms. Nonlinear Process Geophys 11:303
Welling DT, Love JJ, Rigler EJ, Oliveira DM, Komar CM, Morley SK (2021) Numerical simulations of the geospace response to the arrival of an idealized perfect interplanetary coronal mass ejection. Space Weather 19:e2020SW002489. https://doi.org/10.1029/2020SW002489
West HI Jr, Buck RM, Walton JR (1972) Shadowing of electron azimuthal-drift motions near the noon magnetopause. Nat Phys Sci 240:6–7
Wibral M, Pampu N, Priesemann V, Siebenhühner F, Seiwert H, Lindner M, Lizier JT, Vicente R (2013) Measuring information-transfer delays. PLoS ONE 8:e55809
Wing S, Johnson JR, Jen J, Meng C-I, Sibeck DG, Bechtold K, Freeman J, Costello K, Balikhin M, Takahashi K (2005) Kp forecast models. J Geophys Res 110:A04203. https://doi.org/10.1029/2004JA010500
Wing S, Johnson JR, Camporeale E, Reeves GD (2016) Information theoretical approach to discovering solar wind drivers of the outer radiation belt. J Geophys Res Space Phys 121:9378–9399. https://doi.org/10.1002/2016JA022711
Wing S, Johnson J, Vourlidas A (2018) Information theoretic approach to discovering causalities in the solar cycle. Astrophys J 854:85. https://doi.org/10.3847/1538-4357/aaa8e7
Wing S, Johnson JR, Turner DL, Ukhorskiy AY, Boyd AJ (2022) Untangling the solar wind and magnetospheric drivers of the radiation belt electrons. J Geophys Res Space Phys 127:e2021JA030246. https://doi.org/10.1029/2021JA030246
Wintoft P, Lundstedt H, Eliasson L, Kalla L, Hilgers A (2001) Spacecraft anomaly analysis and prediction system – SAAPS. ESA Sci Proc 476:169W
Witt A, Malamud BD (2013) Quantification of long-range persistence in geophysical time series: conventional and benchmark-based improvement techniques. Surv Geophys 34:541–651
Wygant RJ, Torbert RB, Mozer FS (1983) Comparison of S3-3 polar cap potential drops with the interplanetary magnetic field and models of magnetopause reconnection. J Geophys Res 88:5727–5735
Wyner AD (1978) A definition of conditional mutual information for arbitrary ensembles. Inf Control 38:51–59
Xu Z, Zhu L, Sojka J, Kokoszka P, Jach A (2008) An assessment study of the wavelet-based index of magnetic storm activity (WISA) and its comparison to the Dst index. J Atmos Sol-Terr Phys 70:1579
Yiou P, Ghil M, Jouzel J, Paillard D, Vautard R (1994) Nonlinear variability of the climatic system from singular and power spectra of Late Quaternary records. Clim Dyn 9(8):371
Zaourar N, Hamoudi M, Mandea M, Balasis G, Holschneider M (2013) Wavelet-based multiscale analysis of geomagnetic disturbance. Earth Planets Space 65:1525
Zelenyi LM, Kuznetsova MM (1984) Large-scale instabilities of the plasma sheet driven by particle fluxes at the boundary of the magnetosphere. Sov J Plasma Phys 10:190
Zhang J, Richardson IG, Webb DF, Gopalswamy N, Huttunen E, Kasper JC, Nitta NV, Poomvises W, Thompson BJ, Wu C-C, Yashir S, Zhukov AN (2007) Solar and interplanetary sources of major geomagnetic storms (\(\mathrm{Dst} < -100\text{ nT}\)) during 1996-2005. J Geophys Res 112:A10102. https://doi.org/10.1029/2007JA012321
Zhou X-Y, Tsurutani BT (2001) Interplanetary shock triggering of nightside geomagnetic activity: substorms, pseudobreakups and quiescent events. J Geophys Res 106(18):957
Zhou MS, Guo JY, Shen Y, Kong QL, Yuan JJ (2018) Extraction of common mode errors of GNSS coordinate time series based on multi-channel singular spectrum analysis. Chin J Geophys 61:4383
Zotov L, Bizouard C, Shum CK (2016) A possible interrelation between Earth rotation and climatic variability at decadal time-scale. Geod Geodyn 7(3):216–222. https://doi.org/10.1016/j.geog.2016.05.005
Zou S, Moldwin MB, Coster A, Lyons LR, Nicolls MJ (2011) GPS TEC observations of dynamics of the mid-latitude trough during substorms. Geophys Res Lett 38(14)
Acknowledgements
MB is grateful to H.-L. Wei for very useful discussions on NARMAX approach during preparation of this paper. MB acknowledges support provided by the UK Natural Environment Research Council (NERC) Highlight Topic grant NE/P01738X/1 (Rad-Sat).
DV thanks S. Claudepierre for providing the VAP-A/MagEIS electron flux data set.
Funding
Open access funding provided by HEAL-Link Greece. This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #455 “Complex Systems Perspectives Pertaining to the Research of the Near-Earth Electromagnetic Environment”.
SCC acknowledges support from ISSI via the J. Geiss fellowship and AFOSR grant FA8655-22-1-7056.
SW and JJ acknowledge support of NASA Grants NNX16AQ87G, 80NSSC20K0704, 80NSSC19K0843, 80NSSC19K0822, 80NSSC20K0188, 80NSSC20K1279, 80NSSC21K1678, 80NSSC20K1271, 80NSSC22K0515, and 80NSSC21K1321 and NSF grant AGS2131013.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Balasis, G., Balikhin, M.A., Chapman, S.C. et al. Complex Systems Methods Characterizing Nonlinear Processes in the Near-Earth Electromagnetic Environment: Recent Advances and Open Challenges. Space Sci Rev 219, 38 (2023). https://doi.org/10.1007/s11214-023-00979-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-023-00979-7