Inclusive quarkonium production in pp collisions at $\sqrt{s}$ = 5.02 TeV

Abstract

This article reports on the inclusive production cross section of several quarkonium states, $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$, measured with the ALICE detector at the LHC, in pp collisions at $\sqrt{s} = 5.02$ TeV. The analysis is performed in the dimuon decay channel at forward rapidity ($2.5< y < 4$). The integrated cross sections and transverse-momentum ($p_{\textrm{T}}$) and rapidity ($y$) differential cross sections for $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, $\Upsilon \mathrm (1S)$, and the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratios are presented. The integrated cross sections, assuming unpolarized quarkonia, are: $\sigma _{\textrm{J}/\psi }$ ($p_{\textrm{T}} <20$ GeV/c) = 5.88 ± 0.03 ± 0.34$~\mu$b, $\sigma _{\psi \mathrm{(2S)}}$ ($p_{\textrm{T}} <12$ GeV/c) = 0.87 ± 0.06 ± 0.10$~\mu$b, $\sigma _{\Upsilon \mathrm (1S)}$ ($p_{\textrm{T}} <15$ GeV/c) = 45.5 ± 3.9 ± 3.5 nb, $\sigma _{\Upsilon \mathrm{(2S)}}$ ($p_{\textrm{T}} <15$ GeV/c) = 22.4 ± 3.2 ± 2.7 nb, and $\sigma _{\Upsilon \mathrm{(3S)}}$ ($p_{\textrm{T}} <15$ GeV/c) = 4.9 ± 2.2 ± 1.0 nb, where the first (second) uncertainty is the statistical (systematic) one. For the first time, the cross sections of the three $\Upsilon$ states, as well as the $\psi \mathrm{(2S)}$ one as a function of $p_{\textrm{T}}$ and $y$, are measured at $\sqrt{s} = 5.02$ TeV at forward rapidity. These measurements also significantly extend the $\textrm{J}/\psi$ $p_{\textrm{T}}$ reach and supersede previously published results. A comparison with ALICE measurements in pp collisions at $\sqrt{s} = 2.76$, 7, 8, and 13 TeV is presented and the energy dependence of quarkonium production cross sections is discussed. Finally, the results are compared with the predictions from several production models.

1 Introduction

Quarkonium production in high-energy hadronic collisions is an important tool to study the perturbative and non-perturbative aspects of quantum chromodynamics (QCD) calculations [1, 2]. Quarkonia are bound states of either a charm and anti-charm (charmonia) or a bottom and anti-bottom quark pair (bottomonia). In hadronic collisions, the scattering process leading to the production of the heavy-quark pair involves momentum transfers at least as large as twice the mass of the considered heavy quark, hence it can be described with perturbative QCD calculations. In contrast, the binding of the heavy-quark pair is a non-perturbative process as it involves long distances and soft momentum scales. Describing quarkonium production measurements in proton–proton (pp) collisions at various colliding energies represents a stringent test for models and, in particular, for the investigation of the non-perturbative aspects that are treated differently in the various approaches. These measurements also provide a crucial reference for the investigation of the properties of the quark–gluon plasma formed in nucleus–nucleus collisions and of the cold nuclear matter effects present in proton–nucleus collisions [2, 3].

Quarkonium production can be described by various approaches that essentially differ in the treatment of the hadronization part. The Color Evaporation Model (CEM) [4, 5] considers that the quantum state of every heavy-quark pair produced with a mass above its production threshold and below twice the open heavy flavor (D or B meson) threshold production evolves into a quarkonium. In this model, the probability to obtain a given quarkonium state from the heavy-quark pair is parametrized by a constant phenomenological factor. The Color Singlet Model (CSM) [6] assumes no evolution of the quantum state of the pair from its production to its hadronization. Only color-singlet heavy-quark pairs are thus considered to form quarkonium states. Finally, in the framework of Non-Relativistic QCD (NRQCD) [7], both color-singlet and color-octet heavy-quark pairs can evolve towards a bound state. Long Distance Matrix Elements are introduced in order to parametrize the binding probability of the various quantum states of the heavy-quark pairs. They can be constrained from existing measurements and do not depend on the specific production process under study (pp, electron–proton, etc.).

This article presents measurements of the inclusive production cross section of charmonium ($\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$) and bottomonium ($\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$) states in pp collisions at a center-of-mass energy $\sqrt{s} = 5.02$ TeV with the ALICE detector. The analysis is performed in the dimuon decay channel at forward rapidity ($2.5< y < 4$). In this rapidity interval, the total, transverse momentum ($p_{\textrm{T}}$) and rapidity ($y$) differential cross sections for $\textrm{J}/\psi$ as well as the total cross section for $\psi \mathrm{(2S)}$, were published by the ALICE collaboration based on an earlier data sample [8, 9], corresponding to a factor 12 smaller integrated luminosity. These measurements with improved statistical precision supersede the ones from earlier publication. The $p_{\textrm{T}}$ and $y$ differential measurements for the $\psi \mathrm{(2S)}$ and $\Upsilon \mathrm (1S)$ as well as the total cross sections for all the measured $\Upsilon$ states are presented here for the first time at $\sqrt{s} = 5.02$ TeV and at forward rapidity. The $p_{\textrm{T}}$ coverage of the $\textrm{J}/\psi$ measurement is extended up to 20 GeV/$c$.

The inclusive differential cross sections are obtained as a function of $p_{\textrm{T}}$ for $p_{\textrm{T}} < 20$ GeV/$c$ and as a function of $y$ for $p_{\textrm{T}} < 12$ GeV/$c$ for $\textrm{J}/\psi$, for $p_{\textrm{T}} < 12$ GeV/$c$ for $\psi \mathrm{(2S)}$, and for $p_{\textrm{T}} < 15$ GeV/$c$ for $\Upsilon \mathrm (1S)$. Only the $p_{\textrm{T}}$-integrated cross sections are measured for $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$ due to statistical limitations. The inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio is also presented as a function of $p_{\textrm{T}}$ and $y$. The comparison of the $\textrm{J}/\psi$ cross section with recent results from LHCb [10] is discussed. The results are compared with previous ALICE measurements performed at $\sqrt{s} = 2.76$, 7, 8, and 13 TeV [9, 11,12,13]. Earlier comparisons with LHCb quarkonium results at $\sqrt{s} = 7$, 8, and 13 TeV [14,15,16,17] were performed in [9, 12, 13]. Finally, the results are compared with theoretical calculations based on NRQCD and CEM.

The measurements reported here are inclusive and correspond to a superposition of the direct production of quarkonium and of the contribution from the decay of higher-mass excited states (predominantly $\psi \mathrm{(2S)}$ and $\chi _c$ for $\textrm{J}/\psi$, $\Upsilon \mathrm{(2S)}$, $\chi _b$, and $\Upsilon \mathrm{(3S)}$ for $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(3S)}$ and $\chi _b$ for $\Upsilon \mathrm{(2S)}$, and $\chi _b$ for $\Upsilon \mathrm{(3S)}$). For $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$ a non-prompt contribution from beauty hadron decays is also present.

The article is organized as follows: the ALICE detectors used in the analysis and the data sample are briefly described in Sect. 2, the analysis procedure is presented in Sect. 3, and in Sect. 4 the results are discussed and compared with theoretical calculations and measurements at other center-of-mass energies from ALICE.

2 Apparatus and data samples

A detailed description of the ALICE setup and its performance are discussed in Refs. [18, 19]. In this section, the subsystems relevant for this analysis are presented.

Muons from quarkonium decays are detected in the muon spectrometer within the pseudorapidity range¹$-4<\eta <-2.5$ [20]. The muon spectrometer consists of a front absorber located along the beam direction (z) between $-0.9$ and $-5$ m from the interaction point (IP), five tracking stations (MCH), located between $-5.2$ and $-14.4$ m from the IP, an iron wall at $-14.5$ m, and two triggering stations (MTR), placed at $-16.1$ and $-17.1$ m from the IP. Each station is made of two layers of active detection material, with cathode pad and resistive plate techniques employed for the muon detection in the tracking and triggering devices, respectively. A dipole magnet with a 3 T$\times$m field integral deflects the particles in the vertical direction for the measurement of the muon momentum. The hadronic particle flux originating from the collision vertex is strongly suppressed thanks to the front absorber with a thickness of 10 interaction lengths. Throughout the spectrometer length, a conical absorber at small angle around the z axis reduces the background from secondary particles originating from the interaction of large angle primary particles with the beam pipe. The 1.2 m thick iron wall positioned in front of the triggering stations stops the punch-through hadrons escaping the front absorber, as well as low-momentum muons from pion and kaon decays. In addition, a rear absorber downstream of the trigger stations ensures protection against the background generated by beam–gas interactions.

Two layers of silicon pixel detectors (SPD) with a cylindrical geometry, covering $|\eta |<2.0$ and $|\eta |<1.4$, respectively, are used for the determination of the collision vertex. They are the two innermost layers of the Inner Tracking System (ITS) [21] and surround the beam pipe at average radii of 3.9 and 7.6 cm. The T0 quartz Cherenkov counters [22] are made of two arrays positioned on each side of the IP at $-70$ cm and 360 cm. They cover the pseudorapidity ranges $-3.3< \eta < -3.0$ and $4.6< \eta < 4.9$, respectively. The T0 is used for luminosity determination and background rejection. Similarly, the V0 scintillator arrays [23] are located on both sides of the IP at $-90$ and 340 cm and cover the pseudorapidity ranges $-3.7< \eta < -1.7$ and $2.8< \eta < 5.1$, respectively. These are used for triggering, luminosity determination and to reject beam–gas events using offline timing selections together with the T0 detectors.

A minimum bias trigger is issued by the V0 detector [23] when a logical AND of signals from the two V0 arrays on each side of the IP is produced. Single muon, same-sign dimuon, and opposite-sign dimuon triggers are defined by an online estimate of the $p_{\textrm{T}}$ of the muon tracks using a programmable trigger logic circuit. A predefined $p_{\textrm{T}}$ threshold of 0.5 GeV/$c$ is set in order to remove the low-$p_{\textrm{T}}$ muons, mainly coming from $\pi$ and K decays. The muon trigger efficiency reaches $50\%$ at this threshold value and saturates for $p_{\textrm{T}} > 1.5$ GeV/$c$. Events containing an opposite-sign dimuon trigger in coincidence with the minimum bias trigger are selected for the quarkonium analysis.

The data sample of pp collisions at $\sqrt{s} =5.02$ TeV used for the measurements reported in this article was collected in 2017 with the opposite-sign dimuon trigger, and corresponds to an integrated luminosity $L_{\textrm{int}} = 1229.9~\pm ~0.4$ (stat.) ± 22.1 (syst.) nb$^{-1}$ [24]. The luminosity determination is based on dedicated van der Meer scans [25], where the cross sections seen by two different minimum bias triggers based on the V0 and T0 signals are derived [24]. The number of T0- and dimuon-trigger counts measured with scalers on a run-by-run basis without any data acquisition veto is used along with the T0-trigger cross section to calculate the integrated luminosity of the analyzed data sample. Another method, using reconstructed minimum bias events triggered with the V0 detector only, is used as a cross-check of the first method. In this method, the luminosity is computed as the ratio of the number of equivalent minimum bias events over the V0-trigger cross section. The number of equivalent minimum bias events is evaluated as the product of the total number of dimuon-triggered events with the inverse of the probability of having dimuon-triggered events in a minimum bias triggered data sample recorded with only the V0 [26]. The two methods give compatible values and the one based on T0 is used, as it gives a smaller total uncertainty (see Sect. 3.4).

3 Analysis procedure

3.1 Track selection

The number of detected quarkonia is estimated by pairing muons of opposite charges and by fitting their invariant mass ($m_{\mu ^{+}\mu ^{-}}$) distribution. Reconstructed tracks must meet several selection criteria. The pseudorapidity of each muon candidate must be within the geometrical acceptance of the muon spectrometer ($-4< \eta < -2.5$). Muons are identified and selected by applying a matching condition between the tracking system and the trigger stations. A selection on the transverse position $R_{\text {abs}}$ of the muon at the end of the front absorber ($17.6< R_{\text {abs}} < 89.5$ cm) rejects tracks crossing the thickest sections of the absorber. Finally, the contamination from tracks produced by background events, like beam–gas collisions, is reduced by applying a selection on the product of the track momentum and the transverse distance to the primary vertex [27]. Opposite-sign (OS) muon pairs are then formed in the range $2.5< y < 4$. The considered $p_{\textrm{T}}$  interval varies according to the studied resonance given the available data sample: $p_{\textrm{T}} < 20$ GeV/$c$ for $\textrm{J}/\psi$; $p_{\textrm{T}} < 12$ GeV/$c$ for $\psi \mathrm{(2S)}$; $y$-differential and ($p_{\textrm{T}}$,$y$)-differential $\textrm{J}/\psi$ studies; and $p_{\textrm{T}} < 15$ GeV/$c$ for $\Upsilon \mathrm{(nS)}$.

3.2 Signal extraction

A fit to the OS dimuon invariant mass distribution is performed separately for the charmonium and bottomonium mass regions, in each $p_{\textrm{T}}$ and $y$ interval considered. In both cases, a maximum log-likelihood fitting method is used. In order to evaluate the systematic uncertainties on the charmonium and bottomonium signal extraction, several fitting functions and ranges are considered, and the parameters that are fixed during the fitting procedure are varied, as described below.

Fig. 1

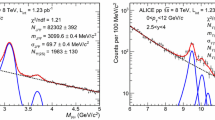
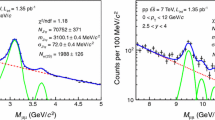
Examples of fit to the OS dimuon invariant mass distribution in the mass region $2< m_{\mu ^{+}\mu ^{-}} < 5$ GeV/$c^{2}$ for $p_{\textrm{T}} < 20$ GeV/$c$ (left), and $7< m_{\mu ^{+}\mu ^{-}} < 13$ GeV/$c^{2}$ for $p_{\textrm{T}} < 15$ GeV/$c$ (right). The $\textrm{J}/\psi$, $\psi$(2S) and $\Upsilon$(nS) signals are modelled with extended Crystal Ball functions, while the background is described by a pseudo Gaussian with a width increasing linearly with the invariant mass. The fit is performed on the full data sample. The widths of the $\psi \mathrm{(2S)}$, $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$, for these examples, are fixed to 73 MeV/$c$, 156 MeV/$c$  and 161 MeV/$c$, respectively

In the charmonium mass region (2 $< m_{\mu ^{+}\mu ^{-}}<$ 5 GeV/$c^{2}$), the fit is performed using the same functional form to describe the $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$ signals, on top of an ad-hoc function to describe the background. The signal shapes considered are either two extended Crystal Ball functions or two pseudo-Gaussian functions [28]. For both functional forms, the $\textrm{J}/\psi$ mass pole and width are left free during the fit procedure, while the $\psi \mathrm{(2S)}$ mass is bound to the $\textrm{J}/\psi$ one by fixing the mass difference between the two states according to the PDG values [29]. The width of the $\psi \mathrm{(2S)}$ signal is also bound to the $\textrm{J}/\psi$ one by means of a scale factor on their ratio. It was obtained via a fit to a large data sample from pp collisions at $\sqrt{s}$ = 13 TeV [9] which gives 1.01 ± 0.05. A variation of +5$\%$ of the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ width ratio central value, corresponding to the difference observed between data and Monte Carlo (MC) simulation at $\sqrt{s} = 13$ TeV,² induces a variation of the $\textrm{J}/\psi$ yield at the per mille level and is therefore neglected, while the impact of this variation on the $\psi \mathrm{(2S)}$ yield enters the systematic uncertainty. The parameters describing the left and right signal tails are the same for both resonances and are fixed to the values extracted from either MC simulations at $\sqrt{s} = 5.02$ TeV using the GEANT3 [30] or the GEANT4 [31] transport codes (see Sect. 3.3), or from fits to the 13 TeV data sample. While the tail parameters can be extracted in $p_{\textrm{T}}$ and $y$ intervals in the MC for both signal shapes, the 13 TeV data sample is only used to constrain the tail parameters of the extended Crystal Ball, when performing a fit to the invariant mass spectrum integrated over $p_{\textrm{T}}$ and $y$. Therefore, when using tail parameters from data, the same set is applied to all the $p_{\textrm{T}}$ and $y$ intervals. Various functions successfully model the background in the invariant mass range $2< m_{\mu ^{+}\mu ^{-}} < 5$ GeV/$c^{2}$. To extract the $\textrm{J}/\psi$ signal, either a pseudo Gaussian with a width increasing linearly with the invariant mass or the ratio of a first order to second order polynomial is used as a background shape. For the $\psi \mathrm{(2S)}$ signal extraction, either a pseudo Gaussian with a width increasing linearly with the invariant mass or the combination of a fourth order polynomial with an exponential function is used to describe the background. In addition to the variation of the background shapes, two different fitting ranges are also used for the evaluation of the signal extraction systematic uncertainties. For each $p_{\textrm{T}}$ and $y$ range, several fits are performed with different combinations of signal shapes, background shapes, fitting ranges, signal tail parameters, and signal width ratios between the two resonances for the $\psi \mathrm{(2S)}$ case. For the charmonium states, the raw yields are computed as the weighted average of the results of all the fits. The statistical uncertainty is the weighted average of the statistical uncertainties of the fits, while the systematic uncertainty is taken as the RMS of the distribution of the results. Given that the choice of the signal tails is the main source of systematic uncertainty, this weight is applied to counterbalance the higher number of fits performed with MC tails with respect to fits with data-driven tails. The raw $\textrm{J}/\psi$ yield is $N_{\textrm{J}/\psi } = 101285 \pm 452$ (stat.) ± 3012 (syst.) for $p_{\textrm{T}} ~<$ 20 GeV/$c$, and the $\psi \mathrm{(2S)}$ raw yield is $N_{\psi \mathrm{(2S)}} = 2086 \pm 133$ (stat.) ± 150 (syst.) for $p_{\textrm{T}} < 12$ GeV/$c$. Figure 1 left shows an example of a fit of the OS dimuon invariant mass distribution in the mass region $2< m_{\mu ^{+}\mu ^{-}} < 5$ GeV/$c^{2}$, separately showing the contributions of the two charmonium resonances and the background. In each $p_{\textrm{T}}$  and $y$  interval, the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ yield ratio is evaluated as the weighted average of the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ yield ratio values obtained from each individual fits (with a given signal shape, background shape, signal tail choice, fitting range and $\psi \mathrm{(2S)}$  width) in order to properly account for correlations in the $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$ signal extraction. The statistical and systematic uncertainties on the ratio are then evaluated in the same way as for the $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$ raw yields.

In the bottomonium mass region ($7< m_{\mu ^{+}\mu ^{-}} < 13$ GeV/$c^{2}$), the $\Upsilon \mathrm{(nS)}$ shapes are parametrized only with extended Crystal Ball functions, since it was checked that the systematic uncertainty related to the choice of the signal shape is negligible compared to other sources. The $\Upsilon \mathrm (1S)$ mass and width are left free in the fit, while the $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$ masses are bound to the $\Upsilon \mathrm (1S)$ one by fixing the mass difference between the states according to the PDG values [29]. The width of the $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$ signals are also bound to the $\Upsilon \mathrm (1S)$ one by factors, $\sigma ^{\textrm{MC}}_{\Upsilon \mathrm{(nS)}} / \sigma ^{\textrm{MC}}_{\Upsilon \mathrm (1S)}$, obtained from MC simulations. Two alternative width scalings, namely $\sigma _{\Upsilon \mathrm{(nS)}}= \sigma _{\Upsilon \mathrm (1S)}$ and $\sigma _{\Upsilon \mathrm{(nS)}}= \sigma _{\Upsilon \mathrm (1S)} \times (2 \times \sigma ^{\textrm{MC}}_{\Upsilon \mathrm{(nS)}} / \sigma ^{\textrm{MC}}_{\Upsilon \mathrm (1S)} - 1)$, are also considered. The $\Upsilon \mathrm{(nS)}$ signal tail parameters must also be fixed while fitting. By default, they are fixed to the values extracted in each given $p_{\textrm{T}}$ and $y$ range from MC simulations performed with the GEANT3 transport code. The same shapes are used for the three $\Upsilon$ resonances. The systematic uncertainty related to the choice of the tail parameters is evaluated for each resonance on the $p_{\textrm{T}}$ and $y$ integrated mass distribution by using several sets of tail parameters that were generated from the fit of the 13 TeV data sample taking into account the correlation among the parameters via the covariance matrix. This uncertainty is then considered to be the same for all $\Upsilon \mathrm (1S)$ $p_{\textrm{T}}$ and $y$ differential intervals. The background shape is described by three empirical functions: an exponential function, a sum of two exponential functions, and a power law function. Additionally, two fit ranges are used. The $\Upsilon \mathrm{(nS)}$ raw yields and statistical uncertainties are then computed as the average of all the fit results and statistical uncertainties, respectively. The systematic uncertainty is the RMS of the fit results summed in quadrature with the uncertainty from the choice of signal tails. The main sources of systematic uncertainty come from the choice of the background description and from the choice of the tail parameters. The $\Upsilon \mathrm{(nS)}$ raw yields are $N_{\Upsilon \mathrm (1S)} = 401 \pm 34$ (stat.) $\pm ~26$ (syst.), $N_{\Upsilon \mathrm{(2S)}} = 153 \pm 22$ (stat.) $\pm ~12$ (syst.), and $N_{\Upsilon \mathrm{(3S)}} = 38 \pm 17$ (stat.) $\pm 7$ (syst.), for $p_{\textrm{T}} < 15$ GeV/$c$. The significance of the $\Upsilon \mathrm{(3S)}$ signal remains rather limited and amounts to 2.4. Figure 1 right shows an example of fit to the OS dimuon invariant mass distribution in the mass region $7< m_{\mu ^{+}\mu ^{-}} < 13$ GeV/$c^{2}$ for $p_{\textrm{T}} < 15$ GeV/$c$, showing the contribution of the three $\Upsilon$ resonances. Similarly to the charmonium case, the $\Upsilon \mathrm{(2S)}$-to-$\Upsilon \mathrm (1S)$ and $\Upsilon \mathrm{(3S)}$-to-$\Upsilon \mathrm (1S)$ raw yield ratios are extracted on a fit-by-fit basis, in order to account for correlations in the signal extraction.

3.3 Acceptance and efficiency corrections

The detector acceptance and reconstruction efficiency $(A \times \varepsilon )$ corrections are applied to the quarkonium raw yields to obtain the corrected yields for the individual resonances. The $(A \times \varepsilon )$ values are estimated via MC simulations by computing the ratio between the number of quarkonia reconstructed in the muon spectrometer and the number of generated quarkonia in given $p_{\textrm{T}}$ and $y$ intervals. Monte Carlo simulations are performed reproducing on a run-by-run basis the detector conditions during the data taking.

In the first stage of the simulation procedure, a parametric generator based on phenomenological $p_{\textrm{T}}$ and y distributions of quarkonia extracted from RHIC, Tevatron, and LHC data [32] is employed, assuming unpolarized resonance production as suggested by the ALICE [33, 34] and LHCb [35,36,37] measurements on polarization parameters for quarkonia that are found small or compatible with zero. The quarkonium decay to $\mu ^+\mu ^-$ is implemented using EVTGEN [38] and PHOTOS [39] to account for the radiative decay of the quarkonium states. The decay muons are tracked through a GEANT3 [30] model of the apparatus that includes a realistic description of the detectors and their performance during data taking. An independent test of the detector simulation has also been performed using the GEANT4 [31] framework. It provides $(A \times \varepsilon )$ results compatible with the GEANT3 simulation within a maximum deviation of 2$\%$.

The $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, and $\Upsilon \mathrm (1S)$ raw yields are divided by the $(A \times \varepsilon )$ correction factors to obtain a first estimate of the $p_{\textrm{T}}$ and $y$ distributions. An iterative procedure is performed to tune the quarkonium input $p_{\textrm{T}}$ and $y$ MC distributions on the measured data distributions until no significant variation of the input shapes is observed. Because of statistical limitations, the iterative procedure cannot be applied to the $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$ as $p_{\textrm{T}}$  and $y$-differential measurements cannot be performed. Since no significant variation of the $y$ input shape between the $\Upsilon \mathrm{(nS)}$ states is expected [40] and the $\Upsilon \mathrm{(nS)}$ $(A \times \varepsilon )$ does not strongly depend on the $p_{\textrm{T}}$ spectrum of the MC input, the $\Upsilon \mathrm (1S)$ $p_{\textrm{T}}$ and $y$ shapes are applied for the $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$.

Table 1 Summary of the systematic uncertainties on the $\textrm{J}/\psi$ cross section, integrated over $p_{\textrm{T}}$, $p_{\textrm{T}}$-differential, $y$-differential, and double differential in $p_{\textrm{T}}$ and $y$. Values marked with an asterisk correspond to uncertainties correlated over $p_{\textrm{T}}$  and/or $y$

Table 2 Summary of the systematic uncertainties on the $\psi \mathrm{(2S)}$ cross section, integrated over $p_{\textrm{T}}$ and $y$, as well as $p_{\textrm{T}}$-differential and $y$-differential. Values marked with an asterisk correspond to uncertainties correlated over $p_{\textrm{T}}$  and/or $y$

Table 3 Summary of the systematic uncertainties on the $\Upsilon \mathrm{(nS)}$ cross section, integrated over $p_{\textrm{T}}$ and $y$, as well as $p_{\textrm{T}}$-differential and $y$-differential for the $\Upsilon \mathrm (1S)$. Values marked with an asterisk correspond to uncertainties correlated over $p_{\textrm{T}}$  and/or $y$

3.4 Systematic uncertainties

The main systematic uncertainties on the quarkonium production cross section (see Eq. 1) come from the following sources: (1) the quarkonium signal extraction, (2) the branching ratio, (3) the determination of the luminosity, and (4) the acceptance and efficiency corrections. The uncertainties on the latter can be broken down into the following contributions: (i) the choice of parametrization for the signal input $p_{\textrm{T}}$ and $y$ distributions, (ii) the tracking efficiency in the muon tracking chambers, (iii) the muon trigger efficiency, and (iv) the matching efficiency between the tracks reconstructed in the muon tracker and the track segments measured in the muon trigger systems.

The evaluation of the systematic uncertainty on quarkonium signal extraction is detailed in Sect. 3.2. It amounts to 3$\%$, 7.2$\%$, 6.5$\%$, 7.8$\%$, and 19$\%$ for the integrated $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$ signals, respectively. This uncertainty is uncorrelated as a function of $p_{\textrm{T}}$ and $y$, for a given quarkonium state. It is, however, partially correlated between $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$, and among the three $\Upsilon \mathrm{(nS)}$ resonances.

The systematic uncertainty on the branching ratio is taken as the current estimate for this quantity according to the PDG [29] and is reported in Tables 1, 2, and 3 for all the states. This uncertainty is fully correlated versus $p_{\textrm{T}}$ and $y$ for a given resonance.

Regardless of the method used to determine the luminosity, its associated systematic uncertainty has two origins: the uncertainty on the normalization factor between the number of triggered events and the equivalent number of minimum bias events, and the uncertainty on the cross section of the minimum bias trigger evaluated using the van der Meer scan technique [24]. The first source of uncertainty is evaluated by using minimum bias triggers issued either by the V0 or the T0 detectors. The two methods are in agreement within 0.5$\%$. This systematic uncertainty is therefore consistently neglected for all resonances and the method which uses the T0 detector is used as the main one since it gives the result with the smallest statistical uncertainty. The second source of uncertainty is the dominant one and arises from the uncertainty on the T0-trigger cross section. It amounts to 1.8$\%$. This uncertainty is fully correlated as a function of $p_{\textrm{T}}$ and $y$ for a given state and also fully correlated among all the quarkonium states.

The systematic uncertainty on $(A \times \varepsilon )$ related to the parametrization of the signal input $p_{\textrm{T}}$ and $y$ distributions has two components. The first one arises from the fact that the corrected yield used to tune the MC input shape in the iterative procedure is obtained from a data sample with an associated statistical uncertainty. This has a negligible impact on the $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$  results, since their reconstructed signals profit from a large sample. For the $\Upsilon \mathrm (1S)$ state, this uncertainty is not negligible and is evaluated by performing 50 fits to the $p_{\textrm{T}}$ and $y$ differential corrected yields after having randomly moved each data point according to a Gaussian smearing within the statistical uncertainty of the data point. The RMS of the resulting distribution of the obtained $(A \times \varepsilon )$ values is assigned as the uncertainty. It varies between 1.3$\%$ and 3.5$\%$. The second component arises from the fact that the correlations in $p_{\textrm{T}}$ and $y$ of the quarkonium input shape are not accounted for in the simulation. It is evaluated by performing several fits to the $y$-differential corrected yields in different $p_{\textrm{T}}$ intervals, and to the $p_{\textrm{T}}$-differential corrected yields in different $y$ intervals. To be conservative, all the possible $p_{\textrm{T}}$ and $y$ input shape combinations are then considered, the $(A \times \varepsilon )$ values are evaluated and the RMS of the results gives the associated uncertainty, ranging between 0.3$\%$ and 4.9$\%$. Such a study can only be performed for the $\textrm{J}/\psi$ since it requires a large data sample to perform double-differential measurements. For the $\psi \mathrm{(2S)}$, the uncertainty from the $p_{\textrm{T}}$  and $y$  double-differential shape variation is assumed to be the same as for the $\textrm{J}/\psi$. Moreover, additional $p_{\textrm{T}}$  and $y$  shapes are considered in the systematic uncertainty evaluation. They are obtained by using the measured $\textrm{J}/\psi$  $p_{\textrm{T}}$  and $y$-dependent cross sections times the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$  cross section ratios. This additional contribution is summed quadratically to the $\textrm{J}/\psi$  one and is below 1.5$\%$ in all $p_{\textrm{T}}$  and $y$  intervals. The resulting total MC input shape systematic uncertainty on the $\psi \mathrm{(2S)}$ ranges between 1.4$\%$ and 5.0$\%$. Given the absence of $p_{\textrm{T}}$  and $y$  double-differential $\Upsilon$ measurements at $\sqrt{s} = 5.02$ TeV, an estimation of the variation of the $\Upsilon \mathrm (1S)$ input shape is performed by fitting the $\Upsilon \mathrm (1S)$ cross sections measured with high statistical precision by LHCb in pp collisions at $\sqrt{s} = 13$ TeV [41], as a function of $y$  in four $p_{\textrm{T}}$ bins and as a function of $p_{\textrm{T}}$  in five $y$  bins. The combination of these 20 input $p_{\textrm{T}}$ and $y$ distributions is used to assess the systematic uncertainty on the $\Upsilon \mathrm (1S)$ $(A \times \varepsilon )$ quantity. Its value ranges between 0.5$\%$ and 1$\%$. For the $\Upsilon \mathrm{(2S)}$ and $\Upsilon \mathrm{(3S)}$, the same MC input systematic uncertainty as the $\Upsilon \mathrm (1S)$ is assumed for the integrated cross section. The two aforementioned sources contributing to the $(A \times \varepsilon )$ uncertainty are uncorrelated and are therefore summed in quadrature, when relevant. The total systematic uncertainty on the $(A \times \varepsilon )$ related to the parametrization of the signal input $p_{\textrm{T}}$ and $y$ distributions is considered uncorrelated as a function of $p_{\textrm{T}}$ and $y$ for a given quarkonium state. In addition, it was checked for the $\textrm{J}/\psi$  that using as MC input shapes the ones obtained from the PYTHIA8 generator [42] instead of the parametrization from Ref. [32] was leading to similar results within the uncertainties discussed above.

The systematic uncertainty on the tracking efficiency in the muon chambers is obtained by comparing data with MC simulation. The single-muon tracking efficiency can be derived, in both data and MC, from the chamber efficiency, which can be evaluated using the redundancy of the tracking information in each station, since a subset of the detector is sufficient for a track to be reconstructed [19]. The differences between the data and MC tracking efficiencies are taken as systematic uncertainty. A 1$\%$ uncertainty is found at the single muon level, hence a 2$\%$ uncertainty applies at the dimuon level for all the resonances. This uncertainty is assumed uncorrelated versus $p_{\textrm{T}}$ and $y$.

The systematic uncertainty on the trigger efficiency has two origins: the differences in shape of the $p_{\textrm{T}}$-dependence of the trigger response function between data and MC in the region close to the trigger threshold, and the intrinsic efficiencies of the muon trigger chambers. The first uncertainty is estimated by comparing the $p_{\textrm{T}}$ dependence, at the single-muon level, of the trigger response function between data and MC. This difference is then propagated at the dimuon level in the MC to evaluate the effect on the quarkonium $(A \times \varepsilon )$ determination. The obtained uncertainty varies, as a function of $p_{\textrm{T}}$ and $y$, between $0.3\%$ and 2.4$\%$ for the $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$, and between $0.3\%$ and 1.1% for the $\Upsilon \mathrm{(nS)}$. The second uncertainty is estimated by comparing the $(A \times \varepsilon )$ obtained in the MC, with a second simulation in which the uncertainties on the trigger chamber efficiencies, as measured from data after varying the track selection criteria, are applied at the detector level, taking into account its segmentation, to blur the trigger response. This uncertainty is 1$\%$ for all the quarkonium states. The uncertainty on the trigger efficiency is uncorrelated as a function of $p_{\textrm{T}}$ and $y$.

The systematic uncertainty associated to the matching efficiency between the tracks reconstructed in the tracking chambers and those reconstructed in the trigger chambers is evaluated from the comparison of the efficiency variation in data and simulation by varying the value of the $\chi ^{2}$ selection applied on the matching condition. It leads to a systematic uncertainty of 1$\%$ common to all the quarkonium resonances, and uncorrelated versus $p_{\textrm{T}}$ and $y$.

Fig. 2

Transverse momentum dependence of the inclusive $\textrm{J}/\psi$ cross section. The measurements are compared to theoretical calculations from Refs. [44,45,46] (left) and Refs. [47,48,49] (right). The calculations of the non-prompt contribution [49] are also shown separately. See text for details

Tables 1, 2, and 3 summarize the systematic uncertainties on the evaluation of the $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, and $\Upsilon \mathrm{(nS)}$ cross section, respectively. Values marked with an asterisk correspond to uncertainties correlated over $p_{\textrm{T}}$  and/or $y$. The total systematic uncertainty for a given quarkonium state is the quadratic sum of all the sources listed in the corresponding table.

The systematic uncertainty on the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$, $\Upsilon \mathrm{(2S)}$-to-$\Upsilon \mathrm (1S)$, and $\Upsilon \mathrm{(3S)}$-to-$\Upsilon \mathrm (1S)$ cross section ratios includes the uncertainty on the signal extraction, MC input, and branching ratio of the resonances. The systematic uncertainties from MCH and MTR efficiencies, and matching efficiency are similar for the ground and excited states and cancel out in the ratio, as do the luminosity uncertainty. The total systematic uncertainty on the integrated $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$  ratio is 10$\%$, while this systematic uncertainty varies between $9\%$ and 16$\%$ as a function of $p_{\textrm{T}}$  and between $8.9\%$ and 15$\%$ as a function of $y$. The total systematic uncertainty on the integrated $\Upsilon \mathrm{(2S)}$-to-$\Upsilon \mathrm (1S)$ [$\Upsilon \mathrm{(3S)}$-to-$\Upsilon \mathrm (1S)$] ratio is 12$\%$ [20$\%$] respectively.

4 Results and discussion

The $p_{\textrm{T}}$- and $y$-differential cross section for inclusive quarkonium production is given by

$$\begin{aligned} \frac{\text {d}^2\sigma }{\text {d}p_{\textrm{T}} \text {d}y} = \frac{N (\Delta y, \Delta p_{\textrm{T}}) }{ L_{\textrm{int}} \times \textrm{BR} \times (A \times \varepsilon ) (\Delta y, \Delta p_{\textrm{T}}) \times \Delta p_{\textrm{T}} \times \Delta y},\nonumber \\ \end{aligned}$$

(1)

where $N (\Delta y, \Delta p_{\textrm{T}})$ is the raw quarkonium yield measured in a given $p_{\textrm{T}}$ and $y$ interval of width $\Delta p_{\textrm{T}}$ and $\Delta y$, respectively. The dimuon branching ratios BR are $(5.96 \pm 0.03)\%$ for $\textrm{J}/\psi$, $(0.80 \pm 0.06) \%$ for $\psi \mathrm{(2S)}$, $(2.48 \pm 0.05)\%$ for $\Upsilon \mathrm (1S)$, $(1.93 \pm 0.17)\%$ for $\Upsilon \mathrm{(2S)}$, and $(2.18 \pm 0.21)\%$ for $\Upsilon \mathrm{(3S)}$ [29].

In this section, the results are given with two uncertainties, the first and second being the statistical and systematic ones, respectively. In the figures, the data points are represented with vertical error bars as statistical uncertainties and with boxes as systematic uncertainties. The correlated systematic uncertainties are quoted as text in the legends.

Fig. 3

Rapidity dependence of the inclusive $\textrm{J}/\psi$ cross section. The measurements are compared to theoretical calculations from Refs. [46, 47]

4.1 Charmonium production

4.1.1 $\textrm{J}/\psi$ cross section

The inclusive $\textrm{J}/\psi$ production cross section in pp collisions at $\sqrt{s} =5.02$ TeV integrated over $2.5< y < 4$ and $p_{\textrm{T}} < 20$ GeV/$c$ is $\sigma _{\textrm{J}/\psi } = 5.88 \pm 0.03$ (stat.) $\pm ~0.34$ (syst.) $\mu$b. The differential cross sections are shown as a function of $p_{\textrm{T}}$ and $y$ in Figs. 2 and 3, respectively. The results are in agreement with the previously published ALICE measurements [8, 9]. A maximum deviation of $1.8\sigma$ for $4<p_{\textrm{T}} <5$ GeV/c and $3.75< y < 4$ is found, where the comparison is performed using the quantity $\sigma _{\textrm{J}/\psi } \times \textrm{BR}$ in order to remove the $\textrm{BR}$ uncertainty. These new measurements extend the $p_{\textrm{T}}$ reach from 12 GeV/$c$ to 20 GeV/$c$. The cross sections are in agreement, within uncertainties, with the recent LHCb results [10]. The inclusive $\textrm{J}/\psi$ double-differential production cross section is shown as a function of $y$ for various $p_{\textrm{T}}$ ranges in the four panels of Fig. 4. These measurements will also serve as reference for studying the nuclear modification of $\textrm{J}/\psi$ production in Pb–Pb collisions. To this purpose, for the $p_{\textrm{T}}$ and $y$ double-differential pp cross sections, $\textrm{J}/\psi$ with $p_{\textrm{T}} <0.3$ GeV/$c$ were excluded to match a similar selection applied in Pb–Pb collisions to remove the photoproduction contribution, occurring besides the hadronic one, and relevant at low $p_{\textrm{T}}$ in peripheral collisions [43].

Fig. 4

Rapidity dependence of the inclusive $\textrm{J}/\psi$ cross section for various $p_{\textrm{T}}$ ranges, compared to theoretical calculations [44,45,46,47,48,49]. The theoretical calculations are scaled as for the data for $0.3<p_{\textrm{T}} <2$ GeV/$c$. See text for details

The cross sections are compared with three theoretical calculations based on NRQCD: two Next-to-Leading Order (NLO) NRQCD calculations from Butenschön et al. [44] and from Ma et al. [45], and a Leading Order (LO) NRQCD calculation coupled to a Color Glass Condensate (CGC) description of the proton structure for low-x gluons from Ma et al. [46], labelled as NRQCD+CGC in the following. They are also compared to two theoretical calculations based on CEM: an improved CEM (ICEM) calculation from Cheung et al. [47] and a NLO CEM calculation from Lansberg et al. [48]. While the NLO calculations presented here are not reliable in the low-$p_{\textrm{T}}$ region ($p_{\textrm{T}} \lesssim M_{\textrm{c}{\bar{c}}}$), the calculations from NRQCD+CGC [46] or the semi-hard approach based on $k_{\textrm{T}}$ factorization of the ICEM model [47] are available also at low $p_{\textrm{T}}$. The theoretical calculations are for prompt $\textrm{J}/\psi$ and account therefore for the decay of $\psi \mathrm{(2S)}$ and $\chi _c$ into $\textrm{J}/\psi$. Since the measurements include as well non-prompt $\textrm{J}/\psi$, their contribution is estimated from Fixed-Order Next-to-Leading Logarithm (FONLL) calculations from Cacciari et al. [49]. The prompt and non-prompt $\textrm{J}/\psi$ calculations are summed in order to obtain inclusive $\textrm{J}/\psi$ calculations to be compared to the measurements. The uncertainties from renormalization and factorization scale and parton distribution function on prompt and non-prompt $\textrm{J}/\psi$ production are considered as uncorrelated.

Fig. 5

The left and right panels show the $p_{\textrm{T}}$ dependence for the inclusive $\psi \mathrm{(2S)}$ production cross section in pp collisions at $\sqrt{s} = 5.02$ TeV. The results are compared with the theory predictions based on NRQCD [44,45,46] (left) and CEM [47, 48] (right) models. The calculation of the non-prompt contribution from FONLL calculations [49] are also shown separately. See text for details

In Figs. 2, 3, and 4 the data are compared with the models described above when calculations are available. A good description of the $p_{\textrm{T}}$ and $y$ distributions of the data is obtained by the NRQCD models for $p_{\textrm{T}} > 3$ GeV/$c$ for the model from Butenschön et al. and $p_{\textrm{T}} > 5$ GeV/$c$ for the model from Ma et al.. The NRQCD+CGC model describes well the data as a function of $p_{\textrm{T}}$ and $y$ for $p_{\textrm{T}} < 8$ GeV/$c$. The ICEM model also gives a good description of the data as a function of $y$ and $p_{\textrm{T}}$ for $p_{\textrm{T}} < 15$ GeV/$c$. It overestimates the data for $p_{\textrm{T}} > 15$ GeV/$c$. Finally, the CEM NLO calculation underestimates the cross sections for $4< p_{\textrm{T}} < 10$ GeV/$c$ and reproduces the data at higher $p_{\textrm{T}}$. The non-prompt $\textrm{J}/\psi$ contribution is also shown in Fig. 2, indicating that the contribution increases with increasing $p_{\textrm{T}}$ from 7% at $p_{\textrm{T}} \approx 1$ GeV/$c$ to $42\%$ for the largest $p_{\textrm{T}}$ interval.

4.1.2 $\psi \mathrm{(2S)}$ cross section

The inclusive $\psi \mathrm{(2S)}$ production cross section in pp collisions at $\sqrt{s}=5.02$ TeV integrated over $p_{\textrm{T}} < 12$ GeV/$c$ and for $2.5< y < 4$ is $\sigma _{\psi \mathrm{(2S)}} = 0.87 \pm 0.06$ (stat.) $\pm ~0.10$ (syst.) $\mu$b. The result is in agreement with the previously published $\psi \mathrm{(2S)}$ cross section [9] and the deviation is found to be $0.75\sigma$ for the quantity $\sigma _{\psi }(2S) \times \textrm{BR}$. An improvement of a factor $\sim$3 for the statistical uncertainty is obtained for the most recent data set. The first results on the $p_{\textrm{T}}$ and $y$ dependence of the inclusive $\psi \mathrm{(2S)}$ cross section for $2.5< y < 4$ in pp collisions at $\sqrt{s} = 5.02$ TeV are shown in Figs. 5 and 6, respectively.

Fig. 6

Rapidity dependence for the inclusive $\psi \mathrm{(2S)}$ production cross section in pp collisions at $\sqrt{s} = 5.02$ TeV. The results are compared with the theory predictions based on NRQCD+CGC [46] and ICEM [47] models. See text for details

Calculations of the same theory models as discussed in Sect. 4.1.1 are compared with the inclusive $\psi \mathrm{(2S)}$ cross section in Figs. 5 and 6. As for the $\textrm{J}/\psi$ case, the experimental measurements include a prompt and a non-prompt contribution while the model calculations are performed for the former only. Therefore, the $\psi \mathrm{(2S)}$ non-prompt contribution, according to FONLL [49], is summed to all theoretical predictions.

In the left panel of Fig. 5, the NRQCD calculation from Butenschön et al. [44] agrees with the experimental data for $4< p_{\textrm{T}} < 12$ GeV/$c$, and the NRQCD calculation from Ma et al. [45] describes well the data except for $5< p_{\textrm{T}} < 6$ GeV/$c$, where it overpredicts them. In addition, in the right panel of Fig. 5 there are significant deviations between the CEM NLO calculation [48] and the data at $p_{\textrm{T}} > 5$ GeV/$c$. The NRQCD+CGC [46] and ICEM [47] models provide a good description of the $\psi \mathrm{(2S)}$ cross section as a function of $p_{\textrm{T}}$ and $y$, albeit with large uncertainties for the $y$  dependence, as it can be seen in Figs. 5 and  6, respectively. Finally, the non-prompt $\psi \mathrm{(2S)}$ contribution from FONLL [49] is also shown in Fig. 5 and varies from $10\%$ to $25\%$ as a function of $p_{\textrm{T}}$.

Fig. 7

The inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio as a function of $p_{\textrm{T}}$ (left) and $y$ (right), compared with theoretical calculations [44, 47, 49]. See text for details

Fig. 8

Transverse momentum dependence of the $\Upsilon \mathrm (1S)$ cross section (left) and $y$ dependence of the $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$ (right) measured by ALICE and CMS. The two panels also show theoretical calculations [48, 51]. See text for details

4.1.3 $\psi \mathrm{(2S)}$ over $\textrm{J}/\psi$ cross section ratio

The ratio between the inclusive $\psi \mathrm{(2S)}$ and inclusive $\textrm{J}/\psi$ production cross sections integrated over $p_{\textrm{T}} < 12$ GeV/$c$ and for $2.5< y < 4$, is $0.15\pm 0.01$ (stat.) $\pm 0.02$ (syst.). In Fig. 7, the $p_{\textrm{T}}$ and $y$ dependence of the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio in pp collisions at $\sqrt{s} = 5.02$ TeV are shown in the left and right panel, respectively. The boxes represent the uncorrelated systematic uncertainties due to the MC input shapes and the signal extraction. The branching-ratio uncertainties, fully correlated versus $p_{\textrm{T}}$  and $y$, are reported in the legend of Fig. 7. All the other systematic uncertainties are correlated over the two resonances and cancel out in the ratio.

The $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ production cross section ratio is also compared with theoretical models. As in previous sections, the non-prompt contribution from FONLL [49] is added to all theoretical calculations. Each individual source of theoretical uncertainty is considered as correlated among the two states and partially cancel in the ratio calculation. The NRQCD calculations from Butenschön et al. [44] describe well the $p_{\textrm{T}}$ dependence of the cross section ratio within the large model uncertainties. A good description of the trend of the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio as a function of $p_{\textrm{T}}$ and $y$ is also provided by the ICEM model [47]. In the left and right panels of Fig. 7, the non-prompt cross section ratios from FONLL [49] are also shown separately for completeness.

Fig. 9

Transverse momentum dependence of the inclusive $\textrm{J}/\psi$ cross section, at forward $y$, measured in pp collisions at $\sqrt{s} = 5.02$, 7 [12], 8 [13], and 13 [9] TeV (top panels), and ratio of the measurements at 5.02, 7, and 8 TeV to the 13 TeV data (bottom panels). The data are compared with the NRQCD theoretical calculations from Butenschön et al. + FONLL (left panels) [44, 49] and with theoretical calculations from ICEM + FONLL (right panels) [47, 49]

4.2 Bottomonium production

The inclusive production cross sections of the three $\Upsilon$ states are measured for the first time in pp collisions at $\sqrt{s} = 5.02$ TeV and for $2.5<y<4$. The cross sections, integrated over $p_{\textrm{T}} < 15$ GeV/$c$ and for $2.5< y < 4$, are:

• $\sigma _{\Upsilon \mathrm (1S)} = 45.5 \pm 3.9$ (stat.) $\pm 3.5$ (syst.) nb,

• $\sigma _{\Upsilon \mathrm{(2S)}} = 22.4 \pm 3.2$ (stat.) $\pm 2.7$ (syst.) nb,

• $\sigma _{\Upsilon \mathrm{(3S)}} = 4.9 \pm 2.2$ (stat.) $\pm 1.0$ (syst.) nb.

The corresponding excited to ground-state ratios amount to:

• $\sigma _{\Upsilon \mathrm{(2S)}} / \sigma _{\Upsilon \mathrm (1S)} = 0.50 \pm 0.08$ (stat.) $\pm 0.06$ (syst.),

• $\sigma _{\Upsilon \mathrm{(3S)}} / \sigma _{\Upsilon \mathrm (1S)} = 0.10 \pm 0.05$ (stat.) $\pm 0.02$ (syst.).

The cross sections are presented in Fig. 8 as a function of $p_{\textrm{T}}$ for the $\Upsilon \mathrm (1S)$ on the left panel and as a function of $y$ for the three $\Upsilon$ states, together with the CMS measurements [50].

The experimental results are compared to ICEM calculations [51] as well as to CEM NLO calculations [48]. Both approaches account for the feed-down contributions from heavier bottomonium states. The two CEM calculations describe the measured $p_{\textrm{T}}$-differential cross section within uncertainties. The $y$ dependence shows that the forward ALICE acceptance covers the region where the production drops from the midrapidity plateau. This observation is in line with the ICEM expectations. The measured $\Upsilon \mathrm{(2S)}$ production cross section lies in the higher limit of the model while the $\Upsilon \mathrm{(3S)}$ result lies at the lower edge of the theory band.

Fig. 10

Rapidity dependence of the inclusive $\textrm{J}/\psi$ (left) and $\psi \mathrm{(2S)}$ (right) cross section, at forward $y$, measured in pp collisions at $\sqrt{s} = 5.02$, 7 [12], 8 [13], and 13 [9] TeV (top panels), and ratio of the measurements at 5.02, 7, and 8 TeV to the 13 TeV data (bottom panels). The data are compared with theoretical calculations from ICEM + FONLL [47, 49]

4.3 Energy dependence of quarkonium production

In Figs. 9 and 10 (left), the $\textrm{J}/\psi$ $p_{\textrm{T}}$- and $y$-differential cross sections measured at $\sqrt{s} = 5.02$ TeV are compared with previous ALICE measurements at $\sqrt{s} = 7$ [12], 8 [13], and 13 TeV [9]. The ratio of the measurements at 5.02, 7, and 8 TeV to the 13 TeV results are also reported as a function of $p_{\textrm{T}}$ at the bottom of Fig. 9 and as a function of $y$ at the bottom of the left panel of Fig. 10. In Fig. 9 (and similarly in Fig. 11 for the $\psi \mathrm{(2S)}$), in order to compute the ratios, the cross sections in some $p_{\textrm{T}}$ intervals had to be merged. In the merged $p_{\textrm{T}}$  intervals, the statistical uncertainty is the quadratic sum of the statistical uncertainties in each $p_{\textrm{T}}$  interval, while the systematic uncertainty is the linear sum of the systematic uncertainties in each $p_{\textrm{T}}$  interval to conservatively account for possible correlations. In Figs. 9, 10 (left), (and similarly in Figs. 10 (right) and 11 for the $\psi \mathrm{(2S)}$), the global systematic uncertainties quoted as text in the top panel contain the branching ratio and luminosity uncertainty for a given energy, while the global systematic uncertainty quoted as text in the bottom panel contains the combination of the luminosity uncertainties at the two corresponding energies. Both the statistical and systematic uncertainties are assumed to be uncorrelated among different energies when computing the cross section ratios.

Thanks to the large data sample used in this analysis, similar integrated luminosities are now collected at 5.02, 7, and 8 TeV, allowing for a systematic comparison of the $\textrm{J}/\psi$ [$\psi \mathrm{(2S)}$] differential yields, up to a $p_{\textrm{T}}$  of 20 GeV/$c$ [12 GeV/c]. The $\textrm{J}/\psi$ $p_{\textrm{T}}$- and $y$-differential cross section values increase, as expected, with increasing collision energy. A stronger hardening of the $p_{\textrm{T}}$  spectra is observed in the collisions at 13 TeV with respect to the 5.02, 7, and 8 TeV data, as can be seen in the ratio displayed at the bottom of Fig. 9. This hardening can derive from the increase of the prompt $\textrm{J}/\psi$  mean $p_{\textrm{T}}$  with energy, as well as by the increasing contribution from non-prompt $\textrm{J}/\psi$  at high $p_{\textrm{T}}$. According to FONLL calculations [49], the fraction of non-prompt $\textrm{J}/\psi$  to the inclusive $\textrm{J}/\psi$  yield, for $p_{\textrm{T}} >12$ GeV/$c$, is about 31$\%$ at 5.02 TeV, 37$\%$ at 7 and 8 TeV, and 40$\%$ at 13 TeV. The central values of the 7-to-13 TeV ratio are closer to the 5.02-to-13 than the 8-to-13 TeV ratio at low $p_{\textrm{T}}$ contrary to the expectation of a smooth increase of the cross section with energy.

Fig. 11

Transverse momentum dependence of the inclusive $\psi \mathrm{(2S)}$ cross section, at forward $y$, measured in pp collisions at $\sqrt{s} = 5.02$, 7 [12], 8 [13], and 13 [9] TeV (top panels), and ratio of the measurements at 5.02, 7, 8 TeV to the 13 TeV data (bottom panels). The data are compared with the NRQCD theoretical calculations from Butenschön et al. + FONLL (left panels) [44, 49] and with theoretical calculations from ICEM + FONLL (right panels) [47, 49]

Fig. 12

Inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio as a function of $p_{\textrm{T}}$, at forward $y$, in pp collisions at $\sqrt{s} ~=~5.02$, 7 [12], 8 [13], and 13 [9] TeV (left panel). The data at $\sqrt{s} = 5.02$ TeV are compared with NRQCD theoretical calculations from Butenschön et al. + FONLL [44, 49] and with theoretical calculations from ICEM + FONLL [47, 49] (right panel)

Fig. 13

Inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio as a function of $y$ in pp collisions at $\sqrt{s} = 5.02$, 7 [12], 8 [13], and 13 [9] TeV (left panel). The data at $\sqrt{s} = 5.02$ TeV are compared with theoretical calculations from ICEM + FONLL [47, 49] (right panel)

The $\textrm{J}/\psi$ $p_{\textrm{T}}$-differential cross sections are compared with the NRQCD theoretical calculations from Butenschön et al. [44] (left) and to ICEM calculations [47] (right). As in Sect. 4.1, a non-prompt contribution from FONLL [49] is added to all the theoretical calculations for charmonium production. The agreement of both model calculations is rather good for all the energies and covered $p_{\textrm{T}}$ ranges, although they both tend to slightly overestimate (or are at the upper edge of) the data at $p_{\textrm{T}} > 12$ GeV/$c$ for ICEM and $p_{\textrm{T}} > 16$ GeV/$c$ for NRQCD from Butenschön, and this is more pronounced for the ICEM computation. The charmonium $p_{\textrm{T}}$- and $y$-differential cross section ratios among different energies can provide stronger constraints on the theoretical models. Indeed, similarly as for the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio in Sect. 4.1.3, the individual uncertainty sources on prompt charmonium (charm mass, renormalization and factorization scale) and non-prompt charmonium (bottom mass, renormalization and factorization scale, and parton distribution function) are considered as correlated among the considered energies and partially cancel in the ratio calculation. On the bottom panels of Fig. 9, the ratios are compared with theoretical calculations from NRQCD from Butenschön et al. [44] (left) and ICEM [47] (right) calculations. The NRQCD calculation is able to successfully describe the 5.02-to-13 TeV and 8-to-13 TeV ratios in the whole $p_{\textrm{T}}$  range of validity of the model, while it slightly overestimates, or is at the upper edge of data, for the 7-to-13 TeV ratio. The ICEM calculation can only satisfactorily describe the 8-to-13 TeV ratio, while the model calculation is systematically above the 5.02-to-13 and the 7-to-13 TeV data, except in the very-low- and very-high-$p_{\textrm{T}}$ region.

In the left panel of Fig. 10, the $\textrm{J}/\psi$ $y$-differential cross section shows a slight decrease with increasing $y$ at all energies. The ratio of the lower energy data to the 13 TeV data exhibits a flat behaviour within the experimental uncertainties for the three energies. The $y$-differential cross sections and cross section ratios between the available energies are also compared to the ICEM model [47]. The model is able to reproduce the cross sections at all energies, as well as the decreasing trend with increasing $y$, but suffers from large theoretical uncertainties. Similarly to what is observed for the $p_{\textrm{T}}$-dependent cross section ratios, the ICEM calculation successfully describes the 8-to-13 TeV ratio over the entire $y$  range, but overestimates, or is at the edges of the 5.02-to-13 and 7-to-13 TeV cross section ratios. The NRQCD model prediction from Butenschön et al. [44], being available only for $p_{\textrm{T}} > 3$ GeV/$c$, cannot be compared to the $p_{\textrm{T}}$-integrated cross section.

The $\psi \mathrm{(2S)}$ $y$-differential cross section is presented in the right panel of Fig. 10. The results at $\sqrt{s}~=~13$ TeV, similarly to the $\textrm{J}/\psi$ ones, show a decreasing trend with increasing $y$, which is less evident at lower energy because of the larger statistical uncertainties. As shown in Fig. 10 (right), the 5.02-to-13, 7-to-13, and 8-to-13 TeV ratios display no strong $y$ dependence within the experimental uncertainties. As for the $\textrm{J}/\psi$, the $y$-differential cross section ratios are compared to the ICEM calculation [47]. The cross sections and their $y$  dependence are well reproduced by the model at the various energies. Within the large experimental uncertainties, the ICEM model is able to reproduce consistently the 5.02-to-13, 7-to-13, and 8-to-13 TeV ratios. The inclusive $\psi \mathrm{(2S)}$ $p_{\textrm{T}}$-differential cross sections measured at $\sqrt{s} = 5.02$, 7, 8, and 13 TeV are compared in Fig. 11. The cross section increases with increasing collision energy. Contrary to the $\textrm{J}/\psi$ case, the 5.02-to-13, 7-to-13, and 8-to-13 TeV ratios in the bottom panel of Fig. 11 exhibit a flat $p_{\textrm{T}}$ dependence for $3 \le p_{\textrm{T}} < 12$ GeV/$c$, indicating that no significant hardening of the $p_{\textrm{T}}$ spectrum is seen, within the data uncertainties, at the highest collision energy with respect to the lower energies. The inclusive $\psi \mathrm{(2S)}$ $p_{\textrm{T}}$-differential cross section and cross section ratios among energies are also compared with the NRQCD calculation from Butenschön et al. [44] (left panel of Fig. 11) and with the ICEM model [47] (right panel of Fig. 11). Both models are able to satisfactorily describe the $\psi \mathrm{(2S)}$ $p_{\textrm{T}}$-differential cross section measurements at all the displayed energies. One can however remark that the NRQCD calculation overestimates systematically the cross sections for 3 $\le p_{\textrm{T}} < 4$ GeV/$c$, and that both the NRQCD and ICEM models are at the lower edges of the measurements for $p_{\textrm{T}} \ge 8$ GeV/$c$ and for $\sqrt{s} = 5.02$, 7, and 8 TeV. Concerning the cross section ratios, the NRQCD model reproduces the 5.02-to-13 and 7-to-13 TeV data for $3 \le p_{\textrm{T}} < 8$ GeV/$c$, and underestimates them for $p_{\textrm{T}} \ge 8$ GeV/$c$ and in almost the whole $p_{\textrm{T}}$ range for the 8-to-13 TeV ratio. Similarly, the ICEM calculation describes successfully the trend versus $p_{\textrm{T}}$  of the 5.02-to-13 and 7-to-13 TeV ratios for $p_{\textrm{T}} < 8$ GeV/$c$, and additionally it provides a reasonable description of the 8-to-13 TeV ratio for $2 \le p_{\textrm{T}} < 8$ GeV/$c$, given the current experimental uncertainties. Both the NRQCD calculation and ICEM model suggest a weak hardening of the $\psi \mathrm{(2S)}$ $p_{\textrm{T}}$  spectrum with the collision energy, which is not observed in data, possibly due to large experimental uncertainties.

Fig. 14

Inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio (left) and $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$ $p_{\textrm{T}}$-integrated cross section per unit of rapidity (right) as a function of the collision energy in pp collisions [9, 11,12,13]. In the left panel, the systematic boxes include the BR uncertainties from both resonances, on top of the MC input and signal extraction systematic uncertainties. The 13 TeV data point is computed from the published individual $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$ $p_{\textrm{T}}$-integrated cross sections. The statistical and systematic uncertainties are assumed to be uncorrelated between the resonances when computing the ratio. In the right panel, the luminosity and branching ratio uncertainties are included in the systematic boxes. The data are compared with theoretical calculations from ICEM + FONLL [47, 49]

The $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio is displayed as a function of $p_{\textrm{T}}$, $y$, and integrated over $p_{\textrm{T}}$ and y for 2.5 $< y<$ 4 for the different pp colliding energies in Figs. 12 (left), 13 (left), and 14 (left), respectively. The $p_{\textrm{T}}$-differential $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio increases with increasing $p_{\textrm{T}}$ and does not exhibit any energy dependence within the current uncertainties. Similarly, no significant change in shape nor in magnitude is observed in the $y$-dependent $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio, which follows a flat trend with $y$. The $y$  and $p_{\textrm{T}}$-integrated $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio for 2.5 $< y<$ 4 is also compatible with no energy dependence within the measurement uncertainties. The $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio as a function of $p_{\textrm{T}}$ is also compared to the NRQCD from Butenschön et al. [44] and ICEM [47] models in the right panel of Fig. 12 for $\sqrt{s}$ = 5.02 TeV and in Fig. 15 of the appendix for $\sqrt{s}$ = 7, 8 and 13 TeV. In both models the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio does not exhibit a strong energy dependence, as in data. The NRQCD model describes within uncertainties the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio at 5.02, 7, and 8 TeV for $p_{\textrm{T}} \ge 3$ GeV/$c$, but it tends to overestimate it at 13 TeV, where the uncertainties are smaller. The ICEM calculation qualitatively describes the $p_{\textrm{T}}$  dependence of the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio at the four energies for $p_{\textrm{T}} < 8$ GeV/$c$, and suggests a flat behaviour for $p_{\textrm{T}}$ $\ge$ 8 GeV/$c$ in agreement with the 13 TeV data which are the most precise ones. In Fig. 13 right, the $y$-differential $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio at $\sqrt{s}$ = 5.02 TeV is compared with the ICEM calculation. Similar data to theory comparison can be found in Fig. 16 of the appendix for pp collisions at $\sqrt{s}$ = 7, 8 and 13 TeV. The model predicts a flat $y$  dependence and properly describes the data at the four energies within the experimental and theoretical uncertainties.

The energy dependence of the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio integrated in $p_{\textrm{T}}$ and $y$ for 2.5 $< y < 4$ is also compared with the ICEM model in Fig. 14 (left). The charmonium cross section ratio does not exhibit a significant energy dependence and is well reproduced by the ICEM model. Finally, the cross section per unit of rapidity for 2.5 $< y<$ 4 and integrated over $p_{\textrm{T}}$ is displayed as a function of the collision energy in the right panel of Fig. 14, for all available ALICE quarkonium measurements. A steady increase of the cross section is observed with increasing $\sqrt{s}$ for all the states. ALICE data are compared with theoretical calculations from ICEM [47]. The model, within its large uncertainties, is able to consistently reproduce the energy dependence of the cross section for all the quarkonium states. However, the $\Upsilon \mathrm{(3S)}$ results lie on the lower edge of the theoretical calculation band.

5 Conclusion

The inclusive production cross sections of $\textrm{J}/\psi$, $\psi \mathrm{(2S)}$, $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$ have been measured with the ALICE detector at forward rapidity ($2.5< y < 4$) in pp collisions at $\sqrt{s}$  = 5.02 TeV. The $\textrm{J}/\psi$ and $\psi \mathrm{(2S)}$ results are in agreement with earlier measurements at the same energy. Thanks to the larger integrated luminosity by a factor 12 of these new measurements, a $p_{\textrm{T}}$ reach up to 20 GeV/$c$ has been achieved for the $\textrm{J}/\psi$, and the double-differential cross section as a function of $p_{\textrm{T}}$ and $y$ could also be extracted. The $\psi \mathrm{(2S)}$ and $\Upsilon \mathrm (1S)$ production cross section and the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio have been measured for the first time as a function of $p_{\textrm{T}}$ and $y$ at forward rapidity, as well as the $p_{\textrm{T}}$-integrated $\Upsilon \mathrm (1S)$, $\Upsilon \mathrm{(2S)}$, and $\Upsilon \mathrm{(3S)}$ cross sections. The collision energy dependence has been discussed for the five quarkonium states and the ratios of the cross sections at $\sqrt{s}$  = 5.02, 7, and 8 TeV to the one obtained at $\sqrt{s}$  = 13 TeV have been presented as a function of $p_{\textrm{T}}$ and $y$. Calculations based on CEM or NRQCD describe well the charmonium and bottomonium cross sections at all collision energies, as well as the $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ ratio, in the kinematic range they cover. The charmonium cross sections and their ratios relative to the values at $\sqrt{s} = 13$ TeV can be described by a NRQCD model within uncertainties. These combined measurements provide additional experimental constraints to quarkonium production models. This is particularly evident for the determination of the cross section calculations, where a reduction in the size of the theory should now be pursued in order to match the experimental precision. Moreover, the $\sqrt{s}$  = 5.02 TeV pp measurements represent a more accurate reference for the measurement of the quarkonium nuclear modification factor in Pb–Pb collisions collected during the LHC Run 2 at the same nucleon–nucleon center-of-mass energy.

Appendix

The $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio is displayed as a function of $p_{\textrm{T}}$ for pp collisions at $\sqrt{s}$ = 7 [12], 8 [13] and 13 TeV [9] in the top left, top right, and bottom left panel of Fig. 15, respectively. It is compared to the NRQCD model from Butenschön et al. [44] and to the ICEM [47] model, as in Fig. 12 right for the results obtained at $\sqrt{s}$ = 5.02 TeV.

Fig. 15

Inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio as a function of $p_{\textrm{T}}$, at forward $y$, in pp collisions at $\sqrt{s}$ = 7 [12] (top left), 8 [13] (top right), and 13 TeV [9] (bottom left). The data are compared with NRQCD theoretical calculations from Butenschön et al. + FONLL [44, 49] and with theoretical calculations from ICEM + FONLL [47, 49]

Fig. 16

Inclusive $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio as a function of $y$ in pp collisions at $\sqrt{s}$ = 7 [12] (top left), 8 [13] (top right), and 13 TeV [9] (bottom left). The data are compared with theoretical calculations from ICEM + FONLL [47, 49]

The $\psi \mathrm{(2S)}$-to-$\textrm{J}/\psi$ cross section ratio is displayed as a function of $y$ for pp collisions at $\sqrt{s}$ = 7 [12], 8 [13] and 13 TeV [9] in the top left, top right, and bottom left panel of Fig. 16, respectively. It is compared with the ICEM [47] calculation, as in Fig. 13 right for the results obtained at $\sqrt{s}$ = 5.02 TeV.