Proton, deuteron and triton flow measurements in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV

Abstract

High-precision measurements of flow coefficients $v_{n}$ ($n = 1 - 4$) for protons, deuterons and tritons relative to the first-order spectator plane have been performed in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV with the High-Acceptance Di-Electron Spectrometer (HADES) at the SIS18/GSI. Flow coefficients are studied as a function of transverse momentum $p_{{\text {t}}}$ and rapidity $y_{{\text {cm}}}$ over a large region of phase-space and for several classes of collision centrality. A clear mass hierarchy, as expected by relativistic hydrodynamics, is found for the slope of $v_{1}$, $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$ where $y^{\prime }$ is the scaled rapidity, and for $v_{2}$ at mid-rapidity. Scaling with the number of nucleons is observed for the $p_{{\text {t}}}$ dependence of $v_{2}$ and $v_{4}$ at mid-rapidity, which is indicative for nuclear coalescence as the main process responsible for light nuclei formation. $v_{2}$ is found to scale with the initial eccentricity $\langle \epsilon _{2} \rangle$, while $v_{4}$ scales with $\langle \epsilon _{2} \rangle ^{2}$ and $\langle \epsilon _{4} \rangle$. The multi-differential high-precision data on $v_{1}$, $v_{2}$, $v_{3}$, and $v_{4}$ provides important constraints on the equation-of-state of compressed baryonic matter.

1 Introduction

Heavy-ion collisions are a tool to investigate the properties of strongly-interacting matter under extreme conditions, such as high temperatures typical for the early phase of the universe and high baryon number densities occurring in compact stellar objects [1]. Especially the latter conditions cannot easily be addressed by ab-initio calculations based on Quantum Chromo-Dynamics (QCD), the theory of strong interaction, but are to be addressed with effective theories. Therefore, measurements are indispensable to determine the properties of dense matter, which can be – in local equilibrium – encoded in the equation-of-state (EOS) [2,3,4].

For non-polarised and equal-size projectile and target nuclei, the azimuthal uniformity of the momentum tensor in the final state is broken by the spatial asymmetry of the initial state at finite impact parameter which is transferred into momentum space via pressure gradients generated by multiple interactions of the matter constituents. The resulting structure of the azimuthal distributions of produced particles is conveniently parametrised by a Fourier decomposition [5] with the coefficients $v_{n}(p_{{\text {t}}},y)$:

$$\begin{aligned} E \frac{d^{3} N}{d p^{3}}= & {} \frac{d^{2} N}{\pi dy d(p_{{\text {t}}}^{2})} \nonumber \\{} & {} \left[ 1 + 2 \sum _{n = 1}^{\infty } v_{n}(p_{{\text {t}}},y) \cos n (\phi - \varPsi _{{\text {RP}}})\right] \, . \end{aligned}$$

(1)

Here, $\phi$ is the azimuthal angle of the particle and $\varPsi _{{\text {RP}}}$ stands for the azimuthal angle of the reaction plane, defined by the beam direction $\vec {z}$ and the direction of the impact parameter $\vec {b}$ of the colliding nuclei. $p_{z} = p \, \cos \theta$ is the momentum component along the beam direction $\vec {z}$ with the laboratory momentum p and the polar angle $\theta$, $p_{{\text {t}}}= p \, \sin \theta$ the one perpendicular to it, and $y = \tanh ^{-1} (p_{z} / E)$ denotes the rapidity of a given particle with energy E in the laboratory frame. The rapidity in the centre-of-mass system is denoted by $y_{{\text {cm}}}= y - \, y_{{\text {proj}}}/ 2$, with the projectile rapidity $y_{{\text {proj}}}$. The coefficients $v_{1}$ and $v_{2}$ quantify the so-called directed and elliptic flow, respectively. More generally, the shape of the anisotropy is quantified by odd coefficients $v_{1}$, $v_{3}$, $v_{5}$ $\dots$ $v_{2n+1}$ and even coefficients $v_{2}$, $v_{4}$ $\dots$ $v_{2n}$. Due to momentum conservation, and assuming that initial-state fluctuations with large eccentricities are absent, the values of even coefficients are expected to be symmetric around mid-rapidity, while the ones of the odd harmonics should change their sign when going from forward to backward centre-of-mass rapidities.

Flow data in the few GeV energy range at BEVALAC and SIS18 have been reported for pions, charged kaons, hyperons, neutrons, as well as protons and many light nuclei. For reviews see [6,7,8,9] and references therein. Most of these data are for a limited phase space or integrated over transverse momenta. High-statistics, multi-differential data on $v_{1}$ and $v_{2}$ for identified particles measured over a large region of phase-space is a valuable extension of the existing world data. In addition, the study of higher-order flow coefficients can provide information about the various contributions to the bulk properties of dense nuclear matter. At RHIC and LHC energies, these were employed to determine the ratios of the shear and bulk viscosity to the entropy density $\eta /s$, and $\zeta /s$, respectively, of high-temperature matter [10, 11]. Attempts to extract $\eta /s$ for dense baryonic matter have been made by comparing various model approaches to the available data [12,13,14,15,16,17], however with large uncertainties. Data on higher-order flow coefficients are essential in order to disentangle the effects of shear and bulk viscosity [17] and can also provide important information on the EOS. A comparison of the proton $v_{3}$, measured by HADES, with UrQMD transport model calculations indicates an enhanced sensitivity to the EOS of the hadronic medium [18, 19]. Other transport model calculations suggest that a non-vanishing value of $v_{4}$, measured at center-of-mass energies of a few GeV, can constrain the nuclear mean field at high net-baryon densities [20]. The E877 collaboration has reported a non-vanishing $v_{4}$ at 10.1$A\text{ GeV }$ [21], but measurements of higher coefficients are generally scarce at low (i.e. AGS and SIS18) energies. A multi-differential measurement of several Fourier coefficients allows for a three-dimensional characterization of heavy-ion collisions in different representations [22,23,24].

The scaling properties of the flow coefficients $v_{n}$ of different order n with the number of nucleons A of the respective nucleus can provide information on the production mechanisms of light nuclei, e.g. via nucleon coalescence [25, 26]. The relation of the $v_{n}$ to the shape of the initial eccentricity of the collision system can shed light on the reaction dynamics and the transport properties of the produced medium.

In this article we present results on flow of protons, deuterons and tritons in Au+Au collisions at a centre-of-mass energy of $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV, corresponding to a kinetic beam energy of 1.23$A\text{ GeV }$. We extend our previous study [22] to multi-differential data on the flow coefficients $v_{1}- v_{4}$ as a function of transverse momentum and rapidity over a large region of phase-space and for several classes of reaction centrality.

The paper is organised as follows. Section 2 introduces the experimental set-up and the particle reconstruction methods, while Sect. 3 discusses the procedures used to determine the flow coefficients. Section 4 presents the results on directed, elliptic and higher harmonics for semi-central collisions. In Sect. 5 our results of $v_{1}$ and $v_{2}$ are compared with existing world data, while in Sect. 6 the scaling properties of the data are discussed. Section 7 presents comparisons to several model calculations. We summarize in Sect. 8.

2 Experimental set-up

HADES is a charged-particle detector consisting of a six-coil toroidal superconducting magnet centered around the beam axis with six identical detection sections located between the coils and covering polar angles between $18^{\circ }$ and $85^{\circ }$ (see Fig. 1). Each sector is equipped with a Ring-Imaging Cherenkov (RICH) detector followed by four layers of Multi-Wire Drift Chambers (MDCs), two in front of and two behind the magnetic field, as well as a scintillator Time-Of-Flight detector (TOF) (polar angle coverage: $44^{\circ }$ – $85^{\circ }$) and Resistive Plate Chambers (RPC) (polar angle coverage: $18^{\circ }$ – $45^{\circ }$). Hadron identification is based on the time-of-flight measured with TOF and RPC, and on the energy-loss information from TOF as well as from the MDC tracking chambers. Electron candidates are in addition selected via their signals in the RICH detector. Combining this information with the track momentum, as determined from the deflection of the tracks in the magnetic field, allows for an identification of charged particles (e.g. pions, kaons or protons).

Fig. 1

Cross section of the HADES set-up during the measurement of Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV. Shown is the arrangement of the different detectors and a magnet coil on one side of the beam pipe

The spectrometer set-up is complemented by the Forward Wall (FW) detector. It consists of 288 scintillator elements of 2.54 cm thickness and three different front area sizes (innermost region: $4 \times 4$ cm$^{2}$, intermediate region: $8 \times 8$ cm$^{2}$ and outermost region: $16 \times 16$ cm$^{2}$) which are read out with photomultipliers. The FW is placed downstream at a 6.8 m distance from the target and covers the polar angles $0.34^{\circ }< \theta < 7.4^{\circ }$. It thus allows for a measurement of the emission angles and the charge states of projectile spectators and is used to determine the event-plane angle. A detailed description of the HADES experiment can be found in [27].

2.1 Data set and event selection

Several triggers are implemented to start the data acquisition. The minimum-bias trigger is defined by a signal in a 60 $\mu \text{ m }$ thick mono-crystalline CVD¹ diamond detector (START) in the beam line [28]. In addition, online Physics Triggers (PT) are used, which are based on hardware thresholds on the TOF signals, proportional to the event multiplicity, corresponding to at least 5 (PT2) or 20 (PT3) hits in the TOF.

By comparing the measured hit multiplicity distribution with Glauber and transport model simulations, it has been estimated that the PT3 trigger is selecting $(43 \pm 4)$ % (PT2 trigger: $(72 \pm 4)$ %) of the total inelastic cross section [29]. The selection of centrality classes is based on the summed hit multiplicity of the TOF and RPC detectors. Four classes are defined, which together cover the 40 % most central collisions in steps of 10 % of the total Au+Au cross section of $6.83 \pm 0.43$ b. Events are selected offline by requiring that their reconstructed global event vertex lies inside the target region, i.e. between $z = -65$ mm and 0 mm along the beam axis. Additionally, only events with at least four hits in the FW with a charge $Z \ge 1$ are used for the reconstruction of the event-plane. It was verified that this criterion does not introduce any significant bias to the centrality selection. The mean number of accepted proton, deuteron and triton candidates are summarized in Table 1.

2.2 Track selection

The flow coefficients are determined for the charged particles detected by the detectors MDC, TOF and RPC. Their trajectories are reconstructed using the MDC information. The resulting tracks are selected according to the quality parameter provided by the employed Runge-Kutta track fitting algorithm $\chi ^{2}_{{\text {RK}}}$ and a maximal Distance of Closest Approach (DCA) of the extrapolated track to the reconstructed primary vertex position. In order to assure a good matching of the tracks to the hits measured in the particle identification detectors TOF and RPC, an additional selection criterion is applied. It involves an upper limit on the quality parameter ${\text {Q}}_{{\text {MM}}} = dx / \sigma _{x}$, which is defined as the deviation of the intersection point of a given reconstructed track from the position of the associated hit in the RPC and TOF detectors, dx, normalized to the corresponding measurement uncertainty, $\sigma _{x}$. The nominal selection values on $\chi ^{2}_{{\text {RK}}}$, DCA and ${\text {Q}}_{{\text {MM}}}$ are summarized in Table 2.

Table 1 The mean multiplicities of accepted proton ($\langle M_{{\text {p}}} \rangle$), deuteron ($\langle M_{{\text {d}}} \rangle$) and triton ($\langle M_{{\text {t}}} \rangle$) candidates (uncorrected raw numbers) for the different centrality classes

Table 2 List of applied track selection and PID criteria. In addition to the nominally applied values, also two variations are given for each selection criterion, which are used for the determination of the systematic uncertainties

2.3 Particle identification

The Particle IDentification (PID) is based on a combined measurement of time-of-flight and energy loss. The time-of-flight, as determined by the TOF and RPC detectors, allows for a separation of particles in different momentum dependent regions of velocity $\beta$. To select protons, deuterons and tritons windows with widths of $n\,\sigma _{\beta }(p)$ with $n = 2.5$ are placed around the corresponding expected $\beta$ values (see also Table 2). The respective resolutions $\sigma _{\beta }(p)$ depend on the particle momenta p and are parametrised accordingly.

In addition, the energy loss ($\text {d}E/\text {d}x$) measurements in the MDCs are employed for PID. This is particularly important to suppress the ${}^{4}\text {He}$ contamination in the deuteron sample, as the two nuclei cannot be separated by time-of-flight alone due to the same Z/A ratio. The variable $Z_{{\text {MDC}}}$ is constructed from the energy loss measured in all four MDC layers, $\text {d}E/\text {d}x_{{\text {exp}}}$, and the theoretically expected value, $\text {d}E/\text {d}x_{{\text {th}}}$,

$$\begin{aligned} Z_{{\text {MDC}}} = \ln \frac{\text {d}E/\text {d}x_{{\text {exp}}}}{\text {d}E/\text {d}x_{{\text {th}}}}\, . \end{aligned}$$

(2)

The selection windows applied to this variable are momentum independent, but different for protons, deuterons and tritons, see Table 2.

Fig. 2

The phase-space coverage of identified protons (left panel), deuterons (middle panel) and tritons (right panel) as accepted in the HADES experiment for Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV as a function of the centre-of-mass rapidity $y_{{\text {cm}}}$ and transverse momentum $p_{{\text {t}}}$ (the curves correspond to the given polar angles $\theta$ in the laboratory system)

The purity of the particle identification procedure is determined by analysing simulated data (see Sect. 3.2) and by fitting the mass distributions, calculated from the measured values of $\beta$ and momentum for different rapidity and transverse momentum intervals, with a function that describes the signal as well as the background component. Phase-space intervals, in which the purity of the particle identification is found to be lower than 80 %, are excluded from further analysis. Also, intervals at the edges of the detector acceptance, i.e. on the borders of the polar angle range $16^{\circ }< \theta < 85^{\circ }$ and the gaps in azimuth between the detector sectors, are excluded. This translates into a rapidity dependent lower transverse momentum cut-off. At very high momenta, phase-space regions are rejected if the accuracy of the momentum measurement is not sufficient. The phase-space coverage for the identified particles is shown in Fig. 2.

3 Determination of flow coefficients

The flow coefficients $v_{n}$ of order n are defined in their relation to the reaction plane angle $\varPsi _{{\text {RP}}}$ as [30, 31]

$$\begin{aligned} v_{n}= \langle \cos [n (\phi - \varPsi _{{\text {RP}}})] \rangle \, . \end{aligned}$$

(3)

Here, $\langle \dots \rangle$ denotes the average over all selected particles and events in a given sample. As the reaction plane is not accessible experimentally, it is replaced by the event-plane angle ($\varPsi _{{\text {EP}}}$) constructed from measured event anisotropies as described in the following.

3.1 Reaction plane reconstruction

For the determination of the event-plane angle $\varPsi _{{\text {EP}}}$, hits of projectile spectators recorded by the FW are used as illustrated in Fig. 3. Projectile spectators are thus measured in the polar angle interval $0.34^{\circ }< \theta < 7.4^{\circ }$. Only those hits are used for which the energy deposit in the scintillator cells and their flight time corresponds to the values expected for spectators with charges of $Z \ge 1$.

Fig. 3

Sketch illustrating the event-plane reconstruction using the projectile spectator hits recorded in the Forward Wall

Fig. 4

The distribution of the first-order event-plane angles $\varPsi _{{\text {EP,1}}}$ for central ($5 - 10$ %, upper panel) and semi-central ($35 - 40$ %, lower panel) Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV. Shown are the distributions before (red circles) and after (blue circles) applying the flattening procedures described in the text

From the azimuthal angles $\phi _{{\text {FW}}}$ of the FW cells hit by spectators, a vector $\vec {Q}_{n} = (Q_{n,x}, Q_{n,y})$ is calculated event-by-event:

$$\begin{aligned} Q_{n,x}= & {} \sum ^{N_{{\text {FW}}}}_{i = 1} w_{i} \; \cos (n \, \phi _{{\text {FW,i}}}) \, , \nonumber \\ Q_{n,y}= & {} \sum ^{N_{{\text {FW}}}}_{i = 1} w_{i} \; \sin (n \, \phi _{{\text {FW,i}}}) \, . \end{aligned}$$

(4)

Here, $N_{{\text {FW}}}$ is the number of detected FW cell hits. The weights $w_{i}$ are here chosen to be $w_{i} = |Z_{i}|$, where $Z_{i}$ is the charge of a given hit as determined via the signal amplitude seen by the FW cell. Because of non-uniformities in the FW acceptance, caused by few dead cells and by deviations of the beam position relative to the nominal centre of the experimental set-up, the distribution of FW hits averaged over many events is not centred around the origin. To correct for this, the individual positions of the FW-hit $X_{{\text {FW}},i}$ and $Y_{{\text {FW}},i}$ are re-centred by the corresponding first moments $(\langle X_{{\text {FW}}} \rangle , \langle Y_{{\text {FW}}} \rangle )$ and scaled by the second moments $(\sigma _{X_{{\text {FW}}}}, \sigma _{Y_{{\text {FW}}}})$, which are calculated for each day of data-taking and centrality class separately. To remove the residual non-uniformities in the event-plane angular distribution an additional flattening procedure was applied [32].

The corresponding event-plane angle of order n is then defined as:

$$\begin{aligned} \varPsi _{{\text {EP,n}}}= \frac{1}{n} \arctan \frac{Q_{n,y}}{Q_{n,x}} \, . \end{aligned}$$

(5)

Figure 4 shows distributions of the first-order event-plane angles before and after applying the above described correction procedure. As a result of the corrections, $\varPsi _{{\text {EP,1}}}$ is distributed uniformly in all centrality classes. The comparison to a flat distribution results in $\chi ^{2}/NDF$ values in the range 0.83–1.09 for the centralities 0–40 %.

Generally, $\varPsi _{{\text {EP,n}}}$ can be determined for each order n. As the reaction plane orientation is mainly connected to the deflection of the projectile spectators, $n = 1$ provides the highest resolution and therefore the first-order event-plane angle $\varPsi _{{\text {EP,1}}}$ is used in the following for the extraction of the observable flow coefficients of all orders:

$$\begin{aligned} v_{n}^{{\text {obs}}} = \langle \cos [n (\phi - \varPsi _{{\text {EP,1}}})] \rangle \, . \end{aligned}$$

(6)

Fig. 5

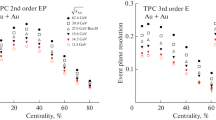
The resolution $\Re _{n}$ of the first-order spectator event plane for flow coefficients of different orders n as a function of the event centrality [22]. The circles correspond to centrality intervals of 5 % width and the squares to 10 % width (curves are meant to guide the eye)

As the computed event-plane angles will fluctuate around the true reaction plane angles, the observed flow coefficients will come out smaller than the true ones. This can be corrected using the resolution correction of the event-plane ($\varPsi _{{\text {EP,1}}}$):

$$\begin{aligned} v_{n}= \frac{v_{n}^{{\text {obs}}}}{\Re _{n}} \, . \end{aligned}$$

(7)

For the first-order event-plane, assuming that non-flow contributions can be neglected, the resolution can be expressed as [30, 31, 33, 34]

$$\begin{aligned} \Re _{n}= & {} \langle \cos [ n \, (\varPsi _{{\text {EP,1}}}- \varPsi _{{\text {RP}}}) ] \rangle \nonumber \\= & {} \frac{\sqrt{\pi }}{2} \, \chi \, e^{- \chi ^{2}/2} \left[ I_{\frac{n - 1}{2}} \left( \frac{\chi ^{2}}{2}\right) + I_{\frac{n + 1}{2}} \left( \frac{\chi ^{2}}{2}\right) \right] \, , \end{aligned}$$

(8)

where $I_{\nu }$ are the modified Bessel functions of the order $\nu$ and $\chi$ is the resolution parameter. For the determination of $\Re _{n}$, the two-sub-event method is employed. For this purpose the FW hits in a given event are randomly divided into two sub-events A and B of equal multiplicity. From the correlation of the two the resolution for the sub-events is then calculated as

$$\begin{aligned} \Re _{n}^{{\text {sub}}}= & {} \langle \cos [ n (\varPsi _{{\text {EP,A(B)}}} - \varPsi _{{\text {RP}}}) ] \rangle \nonumber \\= & {} \sqrt{\langle \cos [ n (\varPsi _{{\text {EP,A}}} - \varPsi _{{\text {EP,B}}}) ] \rangle } \;. \end{aligned}$$

(9)

By replacing $\chi$ in Eq. (8) with $\chi ^{{\text {sub}}}$ and inverting the equation, the value for $\chi ^{{\text {sub}}}$ can be calculated. The value of the resolution parameter for the full FW is then $\chi = \sqrt{2} \; \chi ^{{\text {sub}}}$, which yields the full resolution $\Re _{n}$ after inserting it into Eq. (8).

The resulting values for the resolution of different order n are exhibited in Fig. 5. In the case $n = 1$, it is found to be around 80 % and higher in the centrality range $10 - 40$ %, while it drops towards a value of $\sim 50$ % for very central collisions.

Alternatively, two methods proposed in [30] are used. The resolution parameter $\chi$ is obtained by fitting Eq. (12) of [30] to the measured distribution of the differences between the two sub-event-plane angles $\varDelta \varPsi = |\varPsi _{{\text {EP,A}}} - \varPsi _{{\text {RP,B}}}|$ or by using the approximate relation

$$\begin{aligned} \frac{N(\pi /2< \varDelta \varPsi< \pi )}{N(0< \varDelta \varPsi < \pi )} = \frac{\exp (- \chi ^{2}/2)}{2} \;, \end{aligned}$$

(10)

where the effect of these differences on the systematic uncertainties is found to be negligible.

3.2 Correction for reconstruction inefficiencies

In the high-multiplicity environment of Au+Au collisions the reconstruction of tracks is affected by ambiguities in the assignment of firing MDC drift cells to a given track. This results in reconstruction inefficiencies which depend on the local track multiplicities $N_{{\text {tracks}}}$. Anisotropies in the event shape, as caused by flow effects, will in turn generate local modulations of the track densities and thus of the reconstruction inefficiencies, which consequently distort the determination of the flow coefficients. Therefore, any efficiency correction must also account for the track orientation relative to the event-plane.

Fig. 6

The reconstruction efficiency $\epsilon (\theta ,\varDelta \phi , \text {cent.})$ used for all particles, shown as a function of the polar angle $\theta$ and of the difference between the azimuth angle $\phi$ and the event-plane angle $\phi _{{\text {EP}}} = \phi - \varPsi _{{\text {EP,1}}}$ for two different centrality classes (left: $5 - 10$ %, right: $25 - 30$ %)

Table 3 Summary of the contributions to the absolute systematic uncertainties for different particle species and flow coefficients of different orders. For the $p_{{\text {t}}}$ dependence in different regions of rapidity ($v_{1}$ and $v_{3}$: $-0.25< y_{{\text {cm}}}< -0.15$, $v_{2}$ and $v_{4}$: $|y_{{\text {cm}}}| < 0.05$) and the rapidity dependence in a selected region of $p_{{\text {t}}}$ ($1.0< p_{{\text {t}}}< 1.5$ $\text{ GeV }/c$) the minimal and maximal values are given. In addition to the total systematic uncertainties, also the individual contributions are shown. These are due to the procedures for particle identification (“PID”), the quality selection criteria applied to the tracks (“Track Quality”), the correction for inefficiencies due to high track densities (“Occupancy”) and the effects of an azimuthally non-uniform detector acceptance (“Acceptance”)

With the help of simulated data, generated using Geant3.21 [35] in combination with a detailed description of the detector geometry and response, the multiplicity dependence of the reconstruction efficiency $\epsilon$ was studied. It was found that it can be described by the following function:

$$\begin{aligned} \epsilon (N_{{\text {tracks}}}) = \epsilon _{{\text {max}}} - c_{\epsilon } \, N_{{\text {tracks}}}^{2} \, . \end{aligned}$$

(11)

From simulations, a maximal efficiency of $\epsilon _{{\text {max}}} = 0.98$ is determined. In the phenomenological data-driven approach used here the parameter $c_{\epsilon }$ is adjusted such that $v_{1}= 0$ for $y_{{\text {cm}}}= 0$, as required by the symmetry of the reaction system. In a next step, the average local track multiplicity $\langle N_{{\text {tracks}}}^{{\text {loc.}}} \rangle$ is calculated from data in intervals of the track polar angle $\theta$, of the difference between its azimuth angle $\phi$ and the one of the event-plane $\phi _{{\text {EP}}} = \phi - \varPsi _{{\text {EP,1}}}$ and of the event centrality. Using these three-dimensional matrices as input to Eq. (11), relative efficiency tables $\epsilon (\theta ,\phi _{{\text {EP}}}, \text {cent.})$ are determined. Examples are shown in Fig. 6. These are then used to weight all tracks used to calculate the flow coefficients according to

$$\begin{aligned} w_{{\text {eff}}}(\theta ,\phi _{{\text {EP}}},\text {cent.}) = \frac{1}{\epsilon (\theta ,\phi _{{\text {EP}}},\text {cent.})} \, . \end{aligned}$$

(12)

3.3 Systematic uncertainties

The systematic uncertainties of the measured flow harmonics $v_{n}$ can be separated into global ones, i.e. those which affect all data points in the same way, and those which depend on phase-space position. The latter include effects of the reconstruction and selection of the tracks, particle identification, correction procedures for reconstruction inefficiencies and time-dependent changes of the acceptance. They are determined as a function of $y_{{\text {cm}}}$ and $p_{{\text {t}}}$, separately for each particle species, the order of the flow harmonics $v_{n}$, and the centrality class.

The systematic uncertainties due to the track reconstruction are estimated by varying the track selection cuts. Table 2 lists, in addition to the nominal selection criteria, also two values for each cut used for the determination of systematic effects. Impurities in the selected particle samples, i.e. a background of misidentified particles, will also modify the corresponding flow result. Their contribution to the systematic uncertainty is evaluated by varying the PID selection criteria (see also Table 2).

The parameter $c_{\epsilon }$ used in the correction for multiplicity dependent inefficiencies in Eq. (11) is modified relative to its nominal value to evaluate the influence of the correction procedure on the resulting $v_{n}$. This variation covers all values of $c_{\epsilon }$ which are still compatible within errors with $v_{1}= 0$ at mid-rapidity.

Fig. 7

Left: Result of a toy MC study to investigate the influence of the incomplete acceptance and a non-uniform event-plane on the flow coefficients of different order n. The histogram represents the input values which are compared to the values reconstructed after including the different effects in the simulation. Right: Comparison of the flow coefficients reconstructed from the full data set and from the one including only data with reversed field polarity. Shown are the absolute values $|d v_{1}/d y^{\prime }|_{y^{\prime } = 0}|$, $|v_{2}|$, $|d v_{3}/d y^{\prime }|_{y^{\prime } = 0}|$ and $|v_{4}|$ measured at mid-rapidity for two exemplary $p_{{\text {t}}}$ intervals and the centrality 20–30 %. The data points are scaled for visibility

In larger periods of the data-taking time, one sector of the MDC was not fully operational. As this introduces an azimuthal asymmetry into the acceptance and therefore increases the sensitivity to an imperfect re-centring of the event-plane, it can be the cause of an additional systematic uncertainty. This is estimated by comparing the results obtained for a fully symmetric detector (i.e. six operational sectors) with those for only five sectors. In addition, configurations were analyzed with only four or even three active sectors, corresponding to the upper or lower part of the detector.

The total systematic uncertainly is derived by independently analyzing all different variations and then evaluating the overall distributions of the resulting flow coefficients. It is found that for the even coefficients all the effects described above contribute roughly at the same level to the point-by-point systematic uncertainties, whereas azimuthal anisotropies, like efficiency losses in whole sectors, dominate the systematic uncertainties of the odd flow coefficients. A summary of the different systematic uncertainties is given in Table 3.

In order to verify that the higher flow harmonics are not artificially generated by acceptance holes, a toy MC study was performed. This simulation mimics corresponding effects by passing tracks through an acceptance filter. This filter includes the gaps between the sectors for the support structures and in addition one entirely missing sector. Furthermore, also the effect of a non-uniform event-plane distribution was included. No significant differences between the input values $v_{n}$ and the ones extracted after filtering are observed, see left panel of Fig. 7.

Another systematic check is performed by analysing data that was recorded with a reversed magnetic field setting. In this configuration, the bending directions of positively and negatively charged particles are swapped such that they are measured by different areas in the outer two MDC layers, as well as TOF and RPC. No significant differences between the two settings are found, see right panel of Fig. 7. In addition, the analyses are also performed for each day of data-taking separately, in order to investigate whether any systematic trends appear in the course of the whole data-taking time. Also in this case, no deviations beyond the systematic uncertainty are observed.

Residual systematic effects can also be assessed by investigating whether the Fourier decomposition of the azimuthal particle distributions contains sine terms in addition to the cosine terms in Eq. (1). These are found to be of smaller or similar magnitude than the systematic uncertainties estimated via the methods discussed above. Therefore, no additional systematic uncertainty is assigned due to these differences.

The main contribution to the global systematic uncertainty arises from the event-plane resolution. This is mainly caused by so-called “non-flow” correlations which can distort the event-plane determination. The magnitude of these systematic effects is evaluated using the three-sub-event method, i.e. by determining the event-plane resolution for combinations of different sub-events separated in rapidity. It is found to be below 5 % for the centralities 10–40 % [36].

Fig. 8

The flow coefficients $v_{1}$, $v_{2}$, $v_{3}$, and $v_{4}$ (from top to bottom panels) of protons, deuterons and tritons (from left to right panels) in semi-central (20–30 %) Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV as a function of the centre-of-mass rapidity $y_{{\text {cm}}}$ in transverse momentum intervals of 50 $\text{ MeV }/c$ width. Systematic uncertainties are displayed as boxes. Lines are to guide the eye

Fig. 9

The flow coefficients $v_{1}$, $v_{2}$, $v_{3}$, and $v_{4}$ (from top to bottom panels) of protons, deuterons and tritons (from left to right panels) in semi-central (20–30 %) Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV as a function of $p_{{\text {t}}}$ in several rapidity intervals chosen symmetrically around mid-rapidity. The values measured in the forward hemisphere (open symbols) have been multiplied by $-1$. Systematic uncertainties are displayed as boxes. Lines are to guide the eye

4 Flow coefficients

4.1 Directed flow: $v_{1}$

Figures 8 and 9 present in the uppermost row an overview on the directed flow coefficient $v_{1}$ measured for protons, deuterons and tritons in various $p_{{\text {t}}}$ and $y_{{\text {cm}}}$ intervals in semi-central (20–30 %) Au+Au collisions. While $v_{1}$ of protons is consistent with zero at mid-rapidity, it rises towards forward and decreases towards backward rapidities (see left top panel of Fig. 8). This rapidity dependence is stronger at higher than at lower transverse momenta. The $p_{{\text {t}}}$ dependence of the proton $v_{1}$ is shown in the left top panel of Fig. 9 for four exemplary rapidity intervals. Its absolute value exhibits an almost linear rapid rise in the region $p_{{\text {t}}}< 0.6$ $\text{ GeV }/c$ and then increases only moderately or even saturates for $p_{{\text {t}}}> 1$ $\text{ GeV }/c$. A comparison of the absolute $v_{1}$ values measured in forward and backward rapidity intervals, chosen symmetrically around mid-rapidity, results in an agreement well within systematic errors.

A $p_{{\text {t}}}$ and $y_{{\text {cm}}}$ dependence similar in shape is observed for the $v_{1}$ of deuterons and tritons (middle and right panels in the top row of Figs. 8 and 9). However, there are quantitative differences, namely that the saturation behaviour sets in at higher $p_{{\text {t}}}$ values (above $p_{{\text {t}}}\approx 1.2$ $\text{ GeV }/c$ for deuterons and $p_{{\text {t}}}\approx 1.4$ $\text{ GeV }/c$ for tritons) and reaches higher absolute values of $v_{1}$ (e.g. $|v_{1}^{{\text {prot.}}}| \approx 0.50$, $|v_{1}^{{\text {deut.}}}| \approx 0.60$ and $|v_{1}^{{\text {trit.}}}| \approx 0.68$ for the $|y_{{\text {cm}}}|$ interval 0.55–0.65). This also implies that the dependence of $v_{1}$ on rapidity gets more pronounced with increasing particle mass.

4.2 Elliptic flow: $v_{2}$

Figures 8 and 9 show in the second row a compilation of $v_{2}$ values for protons, deuterons and tritons as a function of $p_{{\text {t}}}$ and $y_{{\text {cm}}}$. Their rapidity dependence is opposite to $v_{1}$, i.e. the absolute value of $v_{2}$ is largest at mid-rapidity and decreases towards forward and backward rapidities for all investigated particles. The $v_{2}$ values around mid-rapidity decrease continuously with $p_{{\text {t}}}$, and an indication for a saturation behaviour is seen at relatively high $p_{{\text {t}}}$ for protons only. The drop with $p_{{\text {t}}}$ is most pronounced for protons and gets weaker with increasing particle mass. Also the rapidity distribution of $v_{2}$ in a fixed $p_{{\text {t}}}$ interval strongly depends on the particle type. While for protons it reaches zero at rapidities of $|y_{{\text {cm}}}| \approx 0.70$, the distributions for deuterons is significantly narrower, such that it crosses zero already at $|y_{{\text {cm}}}| \approx 0.50$ and $v_{2}$ changes sign for larger centre-of-mass rapidities. For tritons this change of sign already happens around $|y_{{\text {cm}}}| \approx 0.35$.

The shape of the $p_{{\text {t}}}$ dependence for deuterons and tritons in the rapidity region, where a positive $v_{2}$ is observed, is clearly different to the one in the regions with negative $v_{2}$. In the region $y_{{\text {cm}}}< -0.5$ ($y_{{\text {cm}}}< -0.35$), $v_{2}$ rises with $p_{{\text {t}}}$ for deuterons (tritons) towards a maximum, whose position seems to move towards higher $p_{{\text {t}}}$ with decreasing $y_{{\text {cm}}}$, and then starts to drop again.

Fig. 10

Directed ($d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$, upper left panel), triangular ($d v_{3}/d y^{\prime }|_{y^{\prime } = 0}$, upper right panel), elliptic ($v_{2}$, lower left panel) and quadrangular ($v_{4}$, lower right panel) flow of protons, deuterons and tritons in two transverse momentum intervals (open symbols: $0.6< p_{{\text {t}}}< 0.9$ $\text{ GeV }/c$ and filled symbols: $1.5< p_{{\text {t}}}< 1.8$ $\text{ GeV }/c$) at mid-rapidity in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV for four centrality classes. Systematic uncertainties are displayed as boxes

4.3 Higher flow harmonics: $v_{3}$ and $v_{4}$

In addition to the directed and elliptic flow coefficients also higher moments of the azimuthal distributions of particle emission relative to the reaction plane have been extracted. In ref. [22] data on flow coefficients up to the sixth order were presented for a limited region of phase-space. A systematic multi-differential analysis of higher orders over a larger $p_{{\text {t}}}- y_{{\text {cm}}}$ range with satisfactory accuracy turned out to be possible only for the coefficients $v_{3}$ and $v_{4}$.

Figures 8 and 9 exhibit in the third row the results on $v_{3}$ for protons, deuterons and tritons. The rapidity and $p_{{\text {t}}}$ dependences are similar for the three analysed particle species (see also Fig. 2 in Ref. [22]). Generally, the rapidity dependence is comparable in shape to the one of $v_{1}$, however, the $v_{3}$ values have opposite signs. Taking a closer look, one finds that the $y_{{\text {cm}}}$ distributions start with a steeper slope at midrapidity than $v_{1}$ and exhibit a turn around away from mid-rapidity. The positions of the corresponding maxima depend slightly on the particle mass and are found at $|y_{{\text {cm}}}| \approx 0.5$ (protons), $\approx 0.4$ (deuterons) and $\approx 0.3$ (tritons). Also, in distinction to $v_{1}$, no clear evidence for a saturation is seen at high $p_{{\text {t}}}$ for $v_{3}$ (see Fig. 9).

Figures 8 and 9 present in the bottom row the results on $v_{4}$ for protons, deuterons and tritons. The rapidity distributions are similar in shape to the ones measured for $v_{2}$ for the corresponding particle, but have opposite signs. Also, they are narrower for $v_{4}$ than for $v_{2}$ and cross the $v_{1}= 0$ line at smaller values of $|y_{{\text {cm}}}|$. For the different particle species this is found to be at $|y_{{\text {cm}}}| \approx 0.35$ (protons), $\approx 0.3$ (deuterons) and $\approx 0.25$ (tritons). The increase of the absolute $v_{4}$ values with $p_{{\text {t}}}$ is also significantly less pronounced as in the case of $v_{2}$. Therefore, in contrast to the case of $v_{2}$, no saturation or even a maximum is observed at higher values of $p_{{\text {t}}}$.

Fig. 11

Compilation of directed and elliptic flow measurements as a function of the subtracted centre-of-mass energy $\sqrt{s_{_{{\text {NN}}}}}- 2 \, m_{N}$. Shown as red points are the slope of $v_{1}$ at mid-rapidity (left panel), $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$, and the $p_{{\text {t}}}$ integrated $v_{2}$ at mid-rapidity (right panel) for protons in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV ($10 - 30$ % centrality). These results are compared to data in the same or similar centrality ranges in Au+Au or Pb+Pb collisions for nuclei with $Z = 1$ (INDRA [7], FOPI [7, 37, 38] Plastic Ball [39, 40]), for protons (FOPI [38, 41], EOS/E895 [42, 43], E877 [44], NA49 [45], STAR [46,47,48], NA61/SHINE [49]) and for inclusive charged particles (E877 [21, 50], CERES [51], WA98 [52], STAR [53, 54], PHOBOS [55])

4.4 Centrality dependences

The directed flow at mid-rapidity can be quantified by its slope $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$ which is defined relative to the scaled rapidity $y^{\prime } = y_{{\text {cm}}}/y_{{\text {mid}}}$, with $y_{{\text {mid}}} = 0.74$ as mid-rapidity in the laboratory system. It is determined as the linear term, $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}= a_{1}$, of a cubic ansatz $v_{1}(y^{\prime }) = a_{1}\,y^{\prime } + a_{3}\,y^{\prime \,3}$ which has been fitted to the measured data points. Similarly, the slope of $v_{3}$ $d v_{3}/d y^{\prime }|_{y^{\prime } = 0}$ is extracted. The upper panels of Fig. 10 displays the corresponding values as determined for two different $p_{{\text {t}}}$ intervals ($0.6< p_{{\text {t}}}< 0.9$ $\text{ GeV }/c$ and $1.5< p_{{\text {t}}}< 1.8$ $\text{ GeV }/c$) and for the four centrality classes investigated in this analysis. The slope of $v_{1}$ exhibits no significant centrality dependence for all particles and $p_{{\text {t}}}$ intervals, except for the very central class where $d v_{1}/d y^{\prime }$ is smaller than for the other centralities. This is distinctly different to the centrality dependence of the slope of $v_{3}$, where the absolute value $|d v_{3}/d y^{\prime }|$ is continuously increasing with centrality. Also, the values are almost identical for the different particles at all centralities, while for $d v_{1}/d y^{\prime }$ a significant mass hierarchy is observed.

Similar to the triangular flow, also $v_{2}$ and $v_{4}$ at mid-rapidity depend on the reaction centrality. While the absolute value $|v_{2}|$ increases roughly linearly with centrality (see lower left panel of Fig. 10), $v_{4}$ exhibits a stronger centrality dependence (see lower right panel of Fig. 10). The mass hierarchy is visible for $v_{2}$ and $v_{4}$ in the lower $p_{{\text {t}}}$ interval for all centrality classes. In the higher $p_{{\text {t}}}$ region, however, only $v_{2}$ of tritons is different from the one of protons and deuterons, while the $v_{4}$ values do not exhibit any systematic ordering.

5 Comparison to world data

The energy dependence of directed and elliptic flow at mid-rapidity and integrated over transverse momentum is presented in Fig. 11. The slope of $v_{1}$ is shown in the left panel and $v_{2}$ at mid-rapidity in the right panel for published data together with our data point. Due to the lack of other measurements in the low-energy region, a similar comparison of $v_{3}$ and $v_{4}$ can not be done.

The slope of $v_{1}$ is characterized by a strong beam energy dependence in the region $E_{{\text {beam}}}/A \lesssim 10$ GeV. While $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$ is negative below $E_{{\text {beam}}}/A \approx$ 0.1 GeV, it is positive at higher energies and rises rapidly towards a maximum at around $E_{{\text {beam}}}/A \approx 1$ GeV and then drops to values close to zero at higher beam energies. The Au+Au reactions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV investigated here are in the region of maximum observable directed flow. A good agreement between the result of this analysis and data measured by the FOPI collaboration [41] is found. The characteristic energy dependence is the result of the interplay between two effects: (i) an increasing pressure of the fireball created in the overlap region of the reaction system, which can push the light spectator nucleons into the reaction plane; (ii) a decreasing passage time of the colliding nuclei, which reduces the pressure transfer onto the light nuclei at higher energies.

Also $v_{2}$ at mid-rapidity exhibits a very distinct energy dependence. In the region $0.1 \lesssim E_{{\text {beam}}}/A \lesssim 5$ GeV $v_{2}$ is negative, i.e. the particle emission is out-of-plane, as the passage time of the spectator matter is long enough to cause the squeeze-out effect [9, 57], i.e. the fireball pressure pushes particles preferentially into the direction which is not shadowed by spectators. At higher energies the passage times are too short and particle emission is in-plane as the pressure gradients are steepest in this direction. The integrated $v_{2}$ obtained for Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV in this analysis is in the region where out-of-plane emission is still very strong. It is also well in accordance with other measurements by EOS [42] and FOPI [38] (see right panel of Fig. 11).

The $p_{{\text {t}}}$ dependence of $v_{2}$ at mid-rapidity measured by HADES is compared with results of other experiments in the same energy region (KaoS [56] and FOPI [38]) in Fig. 12. Within uncertainties and considering the slight differences of beam energies, good agreement with the other data sets is found. The new HADES data extend the phase-space coverage significantly in comparison to previous measurements with clearly improved accuracy.

Fig. 12

Elliptic flow $v_{2}$ of protons in semi-central (20–30 %) Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV as a function of $p_{{\text {t}}}$ at mid-rapidity in comparison with data measured by the KaoS [56] and FOPI [38, 41] collaborations in the same energy region and for similar centrality selections. Systematic uncertainties are displayed as boxes where available

Fig. 13

Elliptic flow $v_{2}$ of protons, deuterons and tritons in semi-central (20–30 %) Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV as a function of $p_{{\text {t}}}$ at mid-rapidity ($|y_{{\text {cm}}}| < 0.05$). The solid curves represent the proton distribution after scaling according to $v_{n,A}(A \, p_{{\text {t}}}) = A \, v_{n}(p_{{\text {t}}})$. The coloured bands depict the results as calculated for the higher-order nucleon-coalescence scenario given in Eq. (13). Systematic uncertainties are displayed as boxes

Fig. 14

Quadrangular flow $v_{4}$ of protons, deuterons and tritons in semi-central (20–30 %) Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV as a function of $p_{{\text {t}}}$ at mid-rapidity ($|y_{{\text {cm}}}| < 0.05$). The dashed curves represent the proton distribution after scaling according the higher order nucleon-coalescence scenario given in Eq. (13). The coloured bands depict the results as calculated with Eq. (15) which includes the additional contribution of $v_{2}$ assuming the relation $v_{2}= - \sqrt{2 \, v_{4}}$. The solid curves show the result for the approximation $v_{n,A}(A \, p_{{\text {t}}}) = A^{2} \, v_{n}(p_{{\text {t}}})$. Systematic uncertainties are displayed as boxes

6 Scaling properties

6.1 Coalescence scaling

A comparison of the $p_{{\text {t}}}$ dependences of $v_{2}$ measured at mid-rapidity for protons, deuterons and tritons (see Fig. 13) demonstrates a clear mass ordering $v_{2}^{{\text {prot.}}}< v_{2}^{{\text {deut.}}} < v_{2}^{{\text {trit.}}}$ for $p_{{\text {t}}}< 1.5$ $\text{ GeV }/c$. Within a naive nucleon-coalescence scenario one would expect that the observed flow coefficients scale with the nuclear mass number A according to the relation $v_{n,A}(A \, p_{{\text {t}}}) =$ $A \, v_{n}(p_{{\text {t}}})$, where $p_{{\text {t}}}$ is the momentum of a single nucleon and $p_{t,A} = A p_{{\text {t}}}$ the one of the composite nuclei. The correspondingly scaled $p_{{\text {t}}}$ dependences of the proton $v_{2}$ are shown in Fig. 13 as solid curves for $A = 2$ and 3. The agreement with the measured $v_{2}$ values for deuterons and tritons is already quite good. However, this approximation only holds for small flow values and, as $v_{2}$ measured at high $p_{{\text {t}}}$ is quite sizeable, a correction term has to be taken into account [25, 26]:

$$\begin{aligned} v_{n,A=2}(2 \, p_{{\text {t}}})= & {} 2 \, v_{n}(p_{{\text {t}}}) \; \frac{1}{1 + 2 \, v_{n}^{2}(p_{{\text {t}}})} \, , \nonumber \\ v_{n,A=3}(3 \, p_{{\text {t}}})= & {} 3 \, v_{n}(p_{{\text {t}}}) \; \frac{1 + v_{n}^{2}(p_{{\text {t}}})}{1 + 6 \, v_{n}^{2}(p_{{\text {t}}})} \, . \end{aligned}$$

(13)

In fact, the correspondingly scaled proton $v_{2}$ values agree well with the ones measured for deuterons and tritons up to the highest $p_{{\text {t}}}$, as depicted by the coloured bands in Fig. 13. It should be noted though, that this kind of scaling is only observed in the region around mid-rapidity, where the elliptic flow is the predominant component of the azimuthal distributions.

Similar to the case of $v_{2}$ (see Fig. 13) also for $v_{4}$ a nuclear mass scaling behaviour is observed at mid-rapidity. This is demonstrated in Fig. 14, which shows a comparison of $v_{4}$ at mid-rapidity as a function of $p_{{\text {t}}}$ for protons, deuterons and tritons. A mass hierarchy can be observed, $v_{4}^{{\text {prot.}}}> v_{4}^{{\text {deut.}}} > v_{4}^{{\text {trit.}}}$, at least in the lower $p_{{\text {t}}}$ region. In order to test whether this ordering of $v_{4}$ is also compatible with a nucleon coalescence scenario, we use an extension of Eq. (13) which takes combinations of different orders into account²:

$$\begin{aligned} v_{4,A=2}(2 \, p_{{\text {t}}})= & {} \frac{2 \, v_{4}(p_{{\text {t}}}) + v_{2}^{2}(p_{{\text {t}}})}{1 + 2 \, v_{2}^{2}(p_{{\text {t}}}) + 2 \, v_{4}^{2}(p_{{\text {t}}})} \, , \nonumber \\ v_{4,A=3}(3 \, p_{{\text {t}}})= & {} \frac{3 \, v_{4}(p_{{\text {t}}}) + 3 \, v_{2}^{2}(p_{{\text {t}}})}{1 + 6 \, v_{2}^{2}(p_{{\text {t}}}) + 6 \, v_{4}^{2}(p_{{\text {t}}})} \, . \end{aligned}$$

(14)

Assuming the relation $v_{2}= - \sqrt{2 \, v_{4}}$ [22] this reduces to

$$\begin{aligned} v_{4,A=2}(2 \, p_{{\text {t}}})= & {} 4 \, v_{4}(p_{{\text {t}}}) \, \frac{1}{1 + 4 \, v_{4}(p_{{\text {t}}}) + 2 \, v_{4}^{2}(p_{{\text {t}}})} \, , \nonumber \\ v_{4,A=3}(3 \, p_{{\text {t}}})= & {} 9 \, v_{4}(p_{{\text {t}}}) \, \frac{1}{1 + 12 \, v_{4}(p_{{\text {t}}}) + 6 \, v_{4}^{2}(p_{{\text {t}}})} \, . \end{aligned}$$

(15)

If the higher-order correction is omitted, this results in the simple approximation of $v_{4,A}(A \, p_{{\text {t}}}) = A^{2} \, v_{4}(p_{{\text {t}}})$, which therefore should only be valid for small flow values. Figure 14 includes a comparison of these different approximations to the data. While the relation given in Eq. (13) does not provide a good match with the data, its extended version given in Eq. (15) results in a very good description of the deuteron and triton data. Also, the simple relation $v_{4,A}(A \, p_{{\text {t}}}) = A^{2} \, v_{4}(p_{{\text {t}}})$ is quite close to the data points, indicating that the higher-order corrections are small.

While the above discussed scaling properties can be indicative for nucleon coalescence as the main process responsible for light nuclei formation, a more refined discussion would involve the comparison to various models. Examples for implementations of the coalescence approach within transport models to describe HADES and STAR flow data, respectively, can be found in [19, 58]. These studies should be extended in the future in a more systematical way using several transport models in order to arrive on firmer conclusions on this topic.

6.2 Initial eccentricity

In order to investigate to what extent the spatial distribution of the nucleons in the initial state of the collision system determines the observed flow pattern, we use the eccentricity $\epsilon _{n}$ of order n of the participant nucleon distribution in the transverse plane as calculated within the Glauber-MC approach [29, 59]:

$$\begin{aligned} \epsilon _{n} = \frac{\sqrt{\langle r^{n} \cos (n\phi ) \rangle ^{2} + \langle r^{n} \sin (n\phi ) \rangle ^{2}}}{\langle r^{n} \rangle } \, , \end{aligned}$$

(16)

with $r = \sqrt{x^{2} + y^{2}}$, $\phi = \tan ^{-1} (y / x)$ and x, y as the nucleon coordinates in the plane perpendicular to the beam axis, where x is oriented in the direction of the impact parameter. The values calculated for the different centrality classes are given in Table 4.

Table 4 Parameters describing the initial nucleon distribution for the different centrality classes as calculated within the Glauber-MC approach [29]. Listed are the corresponding average impact parameter $\langle b \rangle$ and the average participant eccentricities $\langle \epsilon _{2} \rangle$ and $\langle \epsilon _{4} \rangle$

Fig. 15

Scaled elliptic flow of protons, deuterons and tritons in two transverse momentum intervals at mid-rapidity in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV for four centrality classes. The values are divided by the second order eccentricity, $v_{2}/ \langle \epsilon _{2} \rangle$, as calculated within the Glauber-MC approach for the corresponding centrality range (see Table 4). Systematic uncertainties are displayed as boxes

Fig. 16

Same as in Fig. 15, but for the scaled quadrangular flow. The values are divided by the square of second order eccentricity, $v_{4}/ \langle \epsilon _{2} \rangle ^{2}$ (left panel), and by the fourth order eccentricity, $v_{4}/ \langle \epsilon _{4} \rangle$ (right panel)

Figure 15 shows the elliptic flow measured at mid-rapidity for all three investigated particle species after dividing it by the event-by-event averaged second-order participant eccentricity, $v_{2}/\langle \epsilon _{2} \rangle$. Remarkably, this scaling results in almost identical values for all centrality classes at high transverse momenta, indicating that the centrality dependence of the elliptic flow of particles emitted at early times is to a large extent already determined by the initial nucleon distribution. However, as the elliptic flow at these beam energies is due to the so-called squeeze-out effect, caused by the passing spectators, it is not immediately clear how the flow pattern can be directly related to the initial participant distribution. A possible explanation might be that the distribution of the spectators forms a negative image of the one of the participants and thus could imprint its shape onto the emission pattern of the light nuclei. The scaling of $v_{2}$ works less well at lower $p_{{\text {t}}}$, which suggests that particles emitted at later times are less affected by the initial state geometry.

Fig. 17

Directed $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$ (left top panel), elliptic $v_{2}$ (right top panel), triangular $d v_{3}/d y^{\prime }|_{y^{\prime } = 0}$ (left bottom panel) and quadrangular $v_{4}$ (right bottom panel) flow of protons in the transverse momentum interval $0.6< p_{{\text {t}}}< 0.9$ $\text{ GeV }/c$ at mid-rapidity in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV for four centrality classes. The data are compared to several model predictions (see text for details). The width of the bands reflect the statistical uncertainties of the model calculations

Fig. 18

Same as in Fig. 17, but for the transverse momentum interval $1.5< p_{{\text {t}}}< 1.8$ $\text{ GeV }/c$

Also, we observe a scaling of $v_{4}$ with $\epsilon _{2}^{2}$, as depicted in the left panel of Fig. 16 which presents $v_{4}/ \langle \epsilon _{2} \rangle ^{2}$ for different centralities in two transverse momentum intervals. This points to a fixed relation between $v_{2}$ and $v_{4}$, such that the latter is a second order correction $\propto \epsilon _{2}^{2}$ to the overall emission pattern defined at mid-rapidity by $v_{2}$. This is contrary to the case at very high collision energies, where higher-order flow coefficients are related to initial state fluctuations and thus, to a large extent, should be independent of one another. In this scenario one would also expect $v_{4}$ to scale rather with $\epsilon _{4}$. While this might be observable also here at lower $p_{{\text {t}}}$, $v_{4}/ \langle \epsilon _{4} \rangle$ is not independent of centrality in the high $p_{{\text {t}}}$ region, i.e. for particles emitted at early times, as demonstrated in the right panel of Fig. 16.

7 Model comparisons

In the following, several transport model calculations are compared with the measured flow data. These models provide the possibility to test the effect of the EOS of dense nuclear matter on the flow coefficients by implementing different density dependent potentials. Usually, these are parameterised such that the dependence on the baryon density $\rho$ results in either a weak (“soft EOS”) or a strong (“hard EOS”) repulsion of compressed nuclear matter. The comparison with data then allows for a discrimination between these two scenarios. While previous investigations were only based on measurements of the directed and elliptic flow [60, 61], the information from higher-order flow coefficients will provide additional discriminating power. Ultimately, the multi-differential high-statistics data presented here should enable a direct extraction of the EOS parameters via a Bayesian fit of the models to the data. However, as a prerequisite it is important to establish that the various model approaches do not differ significantly in their predictions in order to allow for a consistent determination of the EOS. For a detailed review of the different approaches used for transport simulations see [62,63,64]. As examples the predictions by two QMD models, JAM 1.9 [65] and UrQMD 3.4 [18], and one BUU model, GiBUU 2019 [66] are considered here. The JAM code is used with three different EOS implementations: hard momentum independent NS3, hard momentum dependent MD1 and soft momentum dependent MD4. The UrQMD code is employed with the “hard EOS”, and GiBUU with the “soft EOS” (Skyrme 12).

Comparisons of the model predictions to the proton flow of different order measured at mid-rapidity are presented, as a function of centrality, in Fig. 17 (low $p_{{\text {t}}}$ interval $0.6< p_{{\text {t}}}< 0.9$ $\text{ GeV }/c$) and Fig. 18 (high $p_{{\text {t}}}$ interval $1.5< p_{{\text {t}}}< 1.8$ $\text{ GeV }/c$). As most models do not include a dedicated mechanism for the generation of light clusters, which would be needed for a realistic prediction of deuteron and triton flow, we restrict the comparison here to protons only.

Generally, all models roughly capture the overall magnitude and trend of the measured data. In the lower $p_{{\text {t}}}$ region the differences between the models are relatively small. JAM with MD4 provides the overall best reproduction of the data points, with the exception of $v_{2}$ where MD1 is closer to the data. UrQMD is close to the data for $v_{2}$, but deviates for $v_{1}$, $v_{3}$ and $v_{4}$ at several centralities, while GiBUU reproduces generally better with the exception of $v_{4}$. In the higher $p_{{\text {t}}}$ interval the deviations between the models are a bit larger. Here JAM with MD1 yields the best match to the data, while MD4 and NS3 do not provide a consistent description of the measurements. Also, for UrQMD and GiBUU, systematic deviations are observed for some orders of the flow coefficients. Nevertheless, the models presented here should form a useful basis for further, more detailed data comparisons and and consistent determination of the EOS. It should be noted that not all model calculations include the effects of momentum and isospin dependent potentials, which, however, will be essential for this purpose. Furthermore, a common treatment of cluster formation should be implemented which will allow for an usage of the data on deuteron and triton flow as an additional constraint.

8 Conclusions

In summary, we have presented a detailed multi-differential measurement of collective flow coefficients of protons, deuterons and tritons in Au+Au collisions at $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV using the high-statistics data set collected with the HADES experiment. The directed ($v_{1}$), elliptic ($v_{2}$) and higher order ($v_{3}$ and $v_{4}$) flow coefficients were determined with respect to the first-order event-plane measured at projectile rapidities. The centre-of-mass energy of $\sqrt{s_{_{{\text {NN}}}}}= 2.4$ GeV is close to the region where $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$ is maximal and $v_{2}$ is minimal. All flow coefficients were extracted as a function of transverse momentum $p_{{\text {t}}}$ and rapidity $y_{{\text {cm}}}$ over a large region of phase-space and in four centrality classes. The $p_{{\text {t}}}$ and $y_{{\text {cm}}}$ dependences of $v_{1}$ are very similar in shape for protons, deuterons and tritons. A clear mass hierarchy is observed for $v_{1}$ values measured away from mid-rapidity at higher $p_{{\text {t}}}$, as well as for $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$, which both increase with the mass of the particle. The elliptic flow coefficient $v_{2}$ has a Gaussian shaped rapidity distribution, whose width narrows with increasing particle mass, such that the rapidity value for which $v_{2}$ changes sign moves closer towards mid-rapidity for increasing mass number. Both, the proton directed flow $d v_{1}/d y^{\prime }|_{y^{\prime } = 0}$ and the elliptic flow $v_{2}$ at mid-rapidity are in line with the established energy dependence. The $p_{{\text {t}}}$ and $y_{{\text {cm}}}$ dependences of $v_{3}$ ($v_{4}$) are relatively similar to the one of $v_{1}$ ($v_{2}$), but have the opposite sign. At mid-rapidity a nucleon number scaling is observed in the $p_{{\text {t}}}$ dependence of $v_{2}$ ($v_{4}$), when dividing the values of $v_{2}$ ($v_{4}$) by A ($A^{2}$) and $p_{{\text {t}}}$ by A. This might be indicative for nuclear coalescence as the main process responsible for light nuclei formation. Such a straightforward scaling is not seen at more forward and backward rapidities. The elliptic flow measured at mid-rapidity at higher $p_{{\text {t}}}$ is found to be independent of centrality for all three investigated particle species after dividing it by the event-by-event averaged second order participant eccentricity $v_{2}/\langle \epsilon _{2} \rangle$. A similar scaling is observed for $v_{4}$ after division by $\epsilon _{2}^{2}$.

The new multi-differential high-precision data on $v_{1}$, $v_{2}$, $v_{3}$, and $v_{4}$ provides important constraints on the equation-of-state of compressed baryonic matter as used in models of relativistic nuclear collisions [4]. In particular, the higher moments provide more discriminating power than the directed and elliptic flow alone. The general features of the data on proton flow at mid-rapidity are qualitatively captured by several transport models. A consistent and exact description of all flow coefficients over the whole phase-space and at all investigated centralities is not yet possible. With further progress in the theoretical developments it should be feasible to use the data shown here, together with other measurements, to directly extract a precise parametrization of the equation-of-state of compressed nuclear matter.