$L^p$-strong solution to fluid-rigid body interaction system with Navier slip boundary condition

Abstract

We study a fluid-structure interaction problem describing movement of a rigid body inside a bounded domain filled by a viscous fluid. The fluid is modelled by the generalized incompressible Naiver–Stokes equations which include cases of Newtonian and non-Newtonian fluids. The fluid and the rigid body are coupled via the Navier slip boundary conditions and balance of forces at the fluid-rigid body interface. Our analysis also includes the case of the nonlinear slip condition. The main results assert the existence of strong solutions, in an $L^p-L^q$ setting, globally in time, for small data in the Newtonian case, while existence of strong solutions in $L^p$-spaces, locally in time, is obtained for non-Newtonian case. The proof for the Newtonian fluid essentially uses the maximal regularity property of the associated linear system which is obtained by proving the ${\mathcal {R}}$-sectoriality of the corresponding operator. The existence and regularity result for the general non-Newtonian fluid-solid system then relies upon the previous case. Moreover, we also prove the exponential stability of the system in the Newtonian case.

Appendix: Change of variables

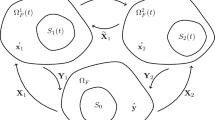
In this section we summarize main facts about the change of variables used to transform the problem to the fixed reference domain. Let us first assume that

$$\begin{aligned} \Vert \varvec{h}\Vert _{L^\infty (0,\infty ;{{\mathbb {R}}}^3)} + \Vert Q-I_3\Vert _{L^\infty (0,\infty ;{{\mathbb {R}}}^3)} \text {diam}(\Omega _S(0))\le \frac{\beta }{2}. \end{aligned}$$

(7.1)

This implies $\text {dist}(\Omega _S(t),\partial \Omega )\ge \beta /2$ for all $t\in [0,\infty )$. For all $\mu >0$, we denote,

$$\begin{aligned} \Omega _\mu = \{\varvec{x}\in \Omega : \text {dist}(\varvec{x},\partial \Omega )>\mu \}. \end{aligned}$$

Now we consider a a cut-off function $\psi \in C^\infty ({{\mathbb {R}}}^3,{{\mathbb {R}}})$ with compact support contained in $\Omega _{\beta /8}$ and equal to 1 in ${\overline{\Omega }}_{\beta /4}$. Let us also introduce the functions $\varvec{w}:{{\mathbb {R}}}^3\times [0,T] \rightarrow {{\mathbb {R}}}^3$ as

$$\begin{aligned} \varvec{w}(\varvec{x},t) = \varvec{l}(t)\times (\varvec{x}-\varvec{h}(t))+\frac{|\varvec{x}-\varvec{h}(t)|^2}{2} \varvec{\omega }(t) \end{aligned}$$

and $\Lambda : {{\mathbb {R}}}^3\times [0,T] \rightarrow {{\mathbb {R}}}^3$ defined as

$$\begin{aligned} \begin{aligned} \Lambda (\varvec{x},t) = \psi (\varvec{x}) \left( \varvec{l}(t)+\varvec{\omega }(t)\times (\varvec{x} - \varvec{h}(t))\right) + \begin{pmatrix} \frac{\partial \psi }{\partial x_2}(\varvec{x})w_3(\varvec{x},t) - \frac{\partial \psi }{\partial x_3}(\varvec{x})w_2(\varvec{x},t)\\ \frac{\partial \psi }{\partial x_3}(\varvec{x})w_1(\varvec{x},t) - \frac{\partial \psi }{\partial x_1}(\varvec{x})w_3(\varvec{x},t)\\ \frac{\partial \psi }{\partial x_1}(\varvec{x})w_2(\varvec{x},t) - \frac{\partial \psi }{\partial x_2}(\varvec{x})w_1(\varvec{x},t) \end{pmatrix}. \end{aligned} \end{aligned}$$

(7.2)

With these definitions, $\Lambda$ satisfies the following lemma (cf. [16, Lemma 2.1]):

Lemma 7.1

Let $\varvec{w}$ and $\Lambda$ be defined as above. Then, we have

• (1) $\Lambda = 0$ outside $\Omega _{\beta /8}$.

• (2) ${\mathrm {div}}\ \Lambda = 0$ in ${{\mathbb {R}}}^3\times [0,T]$.

• (3) $\Lambda (\varvec{x},t) =\varvec{l}(t)+\varvec{\omega }(t)\times (\varvec{x} - \varvec{h}(t))$ for all $\varvec{x}\in \Omega _S(t)$ and $t\in [0,T]$.

• (4) $\Lambda \in C({{\mathbb {R}}}^3\times [0,T],{{\mathbb {R}}}^3)$. $\text {Moreover}$, for all $t\in [0,T], \Lambda (\cdot , t)$ is a $C^\infty$ function and for all $\varvec{x}\in {{\mathbb {R}}}^3$, $\Lambda (\varvec{x},\cdot )\in H^1([0,T],{{\mathbb {R}}}^3)$.

Next consider X be the flow associated to $\Lambda$, satisfying the differential equation

$$\begin{aligned} \begin{aligned} \frac{\partial X}{\partial t}(\varvec{y}, t)&= \Lambda (X(\varvec{y},t), t), \quad t>0\\ X(\varvec{y},0)&= \varvec{y} \in {{\mathbb {R}}}^3. \end{aligned} \end{aligned}$$

(7.3)

We have the following result, proved in [16, Lemma 2.2].

Lemma 7.2

For all $\varvec{y}\in {{\mathbb {R}}}^3$, the initial value problem (7.3) admits a unique solution $X(\varvec{y}, \cdot ):[0,T]\rightarrow {{\mathbb {R}}}^3$ which is a $C^1$ function in [0, T]. Moreover, we have the following properties,

• (1) For all $t\in [0,T]$, the mapping $\varvec{y}\mapsto X(\varvec{y},t)$ is a $C^\infty$-diffeomorphism from ${{\mathbb {R}}}^3$ onto itself and from $\Omega _F(0)$ onto $\Omega _F(t)$.

• (2) Denote by $Y(\cdot , t)$ the inverse of $X(\cdot ,t)$. Then, for all $\varvec{x}\in {{\mathbb {R}}}^3$, the mapping $t\mapsto Y(\varvec{x},t)$ is a $C^1$ function in [0, T].

• (3) For all $\varvec{y}\in {{\mathbb {R}}}^3$ and for all $t\in [0,T]$, the determinant of the Jacobian matrix $J_X$ of $X(\cdot ,t)$ is equal to 1, that is,

  $$\begin{aligned} \mathrm {det} \ J_X(\varvec{y},t) = 1. \end{aligned}$$

From here onwards, $J_X$ and $J_Y$ denote the jacobian matrix of X and Y respectively, that is,

$$\begin{aligned} J_X = \left( \frac{\partial X_i}{\partial y_j} \right) _{ij} \quad \text { and }\quad J_Y = \left( \frac{\partial Y_i}{\partial x_j}\right) _{ij} . \end{aligned}$$

Note that, for each $\varvec{y}\in \Omega _S(0)$, the function $X(\varvec{y},t) = \varvec{h}(t) + Q(t)\varvec{y}, t\ge 0$ is the solution of (7.3), which is easy to verify. This implies, on $\overline{\Omega _S(0)}$,

$$\begin{aligned} J_X = Q \quad \text { and consequently, } \quad J_Y = Q^T. \end{aligned}$$

(7.4)

Similarly, on $\partial \Omega$, $X(\varvec{y},t) = \varvec{y}, t\ge 0$ which yields $J_X = I_3 = J_Y$.

Let us now define the functions: for $(\varvec{y},t)\in \Omega _F(0)\times (0,\infty )$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} {\tilde{\varvec{u}}}(\varvec{y},t) &{}= Q^{-1}(t) \ \varvec{u}(X(\varvec{y},t),t),\\ {\tilde{\pi }}(\varvec{y},t) &{}= \pi (X(\varvec{y},t),t),\\ \tilde{\varvec{l}}(t) &{}= Q^{-1}(t) \ \varvec{l}(t),\\ \tilde{\varvec{\omega }}(t) &{}= Q^{-1}(t) \ \varvec{\omega }(t)\\ {\tilde{J}} &{}= Q^{-1}(t) J(t) Q(t)\\ \tilde{\varvec{n}}(\varvec{y},t) &{}= Q^{-1}(t)\varvec{n}(X(\varvec{y},t),t). \end{aligned} \end{array}\right. } \end{aligned}$$

(7.5)

Notice that $\tilde{\varvec{n}}$ becomes the outward normal at $\Omega _F(0)$. Also, from (1.1) and (7.5)$_4$, it easily follows that

$$\begin{aligned} {\dot{Q}}(t) \varvec{a} = Q(t) (\tilde{\varvec{\omega }}\times \varvec{a}) \quad \forall \varvec{a}\in {{\mathbb {R}}}^3. \end{aligned}$$

(7.6)

In these new variables, the time derivative is transformed into

$$\begin{aligned} \partial _t u_i= & \, ({\dot{Q}}{\tilde{\varvec{u}}})_i + (Q\partial _t {\tilde{\varvec{u}}})_i + (\partial _t X\cdot J_Y^T \nabla )(Q{\tilde{\varvec{u}}})_i \\= & \, \left( Q({\tilde{\omega }}\times {\tilde{\varvec{u}}})\right) _i + (Q\partial _t {\tilde{\varvec{u}}})_i + (\partial _t X\cdot J_Y^T \nabla )(Q{\tilde{\varvec{u}}})_i , \end{aligned}$$

the convection term is transformed into

$$\begin{aligned} (\varvec{u}\cdot \nabla _x)u_i = \left( (Q{\tilde{\varvec{u}}})\cdot (J_Y^T\nabla _y)\right) (Q{\tilde{\varvec{u}}})_i , \end{aligned}$$

the diffusion term is transformed into

$$\begin{aligned} \Delta _x u_i =\sum _{m,l,j} \frac{\partial (Q{\tilde{\varvec{u}}})_i}{\partial y_l} \frac{\partial Y_m}{\partial x_j} \frac{\partial }{\partial y_m}\left( \frac{\partial Y_l}{\partial x_j}\right) + \sum _{m,l,j}\frac{\partial ^2 (Q{\tilde{\varvec{u}}})_i}{\partial y_m \partial y_l} \frac{\partial Y_l}{\partial x_j} \frac{\partial Y_m}{\partial x_j} , \end{aligned}$$

and the pressure is transformed to,

$$\begin{aligned} (\nabla \pi )_i = (J_Y^T \nabla _y{\tilde{\pi }})_i. \end{aligned}$$

Furthermore, we obtain

$$\begin{aligned} {\mathrm {div}}\ \varvec{u}= \nabla _y {\tilde{\varvec{u}}}: (J_Y Q)^T \end{aligned}$$

which can also be written as, by Piola’s identity (cf. [14, p. 39], [25, Ch. 8.1.4.b]),

$$\begin{aligned} \nabla _y {\tilde{\varvec{u}}}: (J_Y Q)^T = {\mathrm {div}}_y\left( (J_Y Q){\tilde{\varvec{u}}}\right) \end{aligned}$$

since $J_Y Q = \mathrm {cof} (Q J_X) = \mathrm {cof}\nabla _y (QX)$ because of $\mathrm {det}J_X =1$. Concerning the boundary condition, we calculate the symmetric gradient,

$$\begin{aligned} (\nabla _x \varvec{u})_{ij} = \partial _j u_i = \sum _{l=1}^3 \frac{ \partial (Q{\tilde{\varvec{u}}})_i}{\partial y_l} \frac{\partial Y_l}{\partial x_j} = \sum _{l,k=1}^3 Q_{ik} \frac{\partial {\tilde{\varvec{u}}}_k}{\partial y_l} \frac{\partial Y_l}{\partial x_j} = (Q \nabla _y {\tilde{\varvec{u}}} J_Y)_{ij}. \end{aligned}$$

This shows that at the interface $\partial \Omega _S(0)$, because of (7.4), $\nabla _x \varvec{u}= Q \, \nabla _y {\tilde{\varvec{u}}} \, Q^{T}$ and hence, $(\nabla _x \varvec{u})^T = Q (\nabla _y {\tilde{\varvec{u}}})^T Q^{T}$ which gives,

$$\begin{aligned} {\mathbb {D}}_x\varvec{u}= Q \,{\mathbb {D}}_y{\tilde{\varvec{u}}}\, Q^T \end{aligned}$$

and consequently,

$$\begin{aligned} \sigma (\varvec{u},\pi ) = Q\sigma ({\tilde{\varvec{u}}},{\tilde{\pi }})Q^T . \end{aligned}$$

Therefore, the slip boundary condition becomes,

$$\begin{aligned}{}[\sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{\varvec{n}}}]_{\varvec{\tau }} + \alpha {\tilde{\varvec{u}}}_{\varvec{\tau }} = \alpha \left( \tilde{\varvec{l}}+\tilde{\varvec{\omega }}\times \varvec{y}\right) _{\varvec{\tau }} \quad \text { on } \quad \partial \Omega _S(0) \end{aligned}$$

and similarly at $\partial \Omega$. It can be shown as in [32, Theorem 2.5] that the fluid part of the original problem (2.1) admits a strong solution $(\varvec{u},\pi )$ if and only if there exists a corresponding solution $({\tilde{\varvec{u}}},{\tilde{\pi }}) \in W^{2,1}_{q,p}(Q^\infty _F) \times L^p(0,\infty ;W^{1,q}(\Omega _F(0)))$ to the fluid part of the transformed problem (7.7).

Next, we write the equations for rigid body. From (7.5)$_3$, we find that

$$\begin{aligned} m\varvec{l}^{\prime}(t) = m ({\dot{Q}}\tilde{\varvec{l}}+ Q\tilde{\varvec{l}}^{\prime})= mQ(\tilde{\varvec{\omega }}\times \tilde{\varvec{l}}) + mQ \tilde{\varvec{l}}^{\prime}. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \int \displaylimits _{\partial \Omega _S(t)}{\sigma (\varvec{u},\pi )\varvec{n}} = Q \int \displaylimits _{\partial \Omega _S(0)}{\sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{n}}} \end{aligned}$$

and

$$\begin{aligned} \int \displaylimits _{\partial \Omega _S(t)}{(\varvec{x} - \varvec{h}(t))\times \sigma (\varvec{u},\pi )\varvec{n}} = Q \int \displaylimits _{\partial \Omega _S(0)}{\varvec{y}\times \sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{n}}}. \end{aligned}$$

Therefore, the equation of linear momentum becomes,

$$\begin{aligned} m \tilde{\varvec{l}}' +m \tilde{\varvec{\omega }} \times \tilde{\varvec{l}}= - \int \displaylimits _{\partial \Omega _S(0)}{\sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{\varvec{n}}}}. \end{aligned}$$

Similarly, using the following identity, for any special orthogonal matrix $M\in SO(3),$

$$\begin{aligned} Ma \times Mb = M(a\times b) \quad \forall a,b \in {{\mathbb {R}}}^3, \end{aligned}$$

the equation of angular momentum becomes,

$$\begin{aligned} {\tilde{J}} \tilde{\varvec{\omega }}^{\prime}(t) - {\tilde{J}} \tilde{\varvec{\omega }}\times \tilde{\varvec{\omega }} = - \int \displaylimits _{\partial \Omega _S(0)}{\varvec{y}\times \sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{\varvec{n}}}}. \end{aligned}$$

Note that, ${\tilde{J}}$ is independent of time, since

$$\begin{aligned} {\tilde{J}}a\cdot b = \int \displaylimits _{\partial \Omega _S(0)}{\rho _S(\varvec{y})(a\times \varvec{y})\cdot (b\times \varvec{y})\mathrm {d}y} \quad \forall a,b\in {{\mathbb {R}}}^3. \end{aligned}$$

Therefore, on the cylindrical domain $\Omega _F(0)\times (0,T)$, the coupled system for the Newtonian fluid (2.1) transforms into,

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} {\tilde{\varvec{u}}}_t - \Delta {\tilde{\varvec{u}}} + \nabla {\tilde{\pi }} &{}= \varvec{F}_0({\tilde{\varvec{u}}}, {\tilde{\pi }}, \tilde{\varvec{l}}, \tilde{\varvec{\omega }})\ &{}&{}\text { in } \Omega _F(0)\times (0,T),\\ {\mathrm {div}}\ {\tilde{\varvec{u}}} &{}= {\mathcal {G}}({\tilde{\varvec{u}}}, \tilde{\varvec{l}}, \tilde{\varvec{\omega }}) = {\mathrm {div}}\ \varvec{H}({\tilde{\varvec{u}}}, \tilde{\varvec{l}}, \tilde{\varvec{\omega }}) \ &{}&{}\text { in } \Omega _F(0)\times (0,T),\\ {\tilde{\varvec{u}}}&{}=\varvec{0} \ &{}&{}\text { on } \ \partial \Omega \times (0,T),\\ {\tilde{\varvec{u}}}\cdot {\tilde{\varvec{n}}}={\tilde{\varvec{u}}}_S\cdot {\tilde{\varvec{n}}}, \quad &{}\left[ \sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{\varvec{n}}}\right] _{\varvec{\tau }}+\alpha {\tilde{\varvec{u}}}_{\varvec{\tau }}=\alpha {\tilde{\varvec{u}}}_{S\varvec{\tau }} \ &{}&{}\text { on } \ \partial \Omega _S(0) \times (0,T),\\ m \tilde{\varvec{l}}' &{}= - \int \displaylimits _{\partial \Omega _S(0)}{\sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{\varvec{n}}}} + \varvec{F}_1(\tilde{\varvec{l}},\tilde{\varvec{\omega }}), \ &{}&{}\ t\in (0,T),\\ {\tilde{J}} \tilde{\varvec{\omega }}' &{}= - \int \displaylimits _{\partial \Omega _S(0)}{\varvec{y}\times \sigma ({\tilde{\varvec{u}}},{\tilde{\pi }}){\tilde{\varvec{n}}}} + \varvec{F}_2(\tilde{\varvec{\omega }}), \ &{}&{}\ t\in (0,T),\\ {\tilde{\varvec{u}}}(0) &{}= \varvec{u}_0 \ &{}&{}\text { in } \ \Omega _F(0),\\ \tilde{\varvec{l}}( 0) = \varvec{l}_0, \quad &{}\tilde{\varvec{\omega }}(0) = \varvec{\omega }_0 \end{aligned} \end{array}\right. } \end{aligned}$$

(7.7)

where

$$\begin{aligned}&{\tilde{\varvec{u}}}_S := \tilde{\varvec{l}} + \tilde{\varvec{\omega }}\times \varvec{y} ;(\varvec{F}_0)_{i}({\tilde{\varvec{u}}}, {\tilde{\pi }}, \tilde{\varvec{l}}, \tilde{\varvec{\omega }}) := \left( (I_3-Q)\partial _t {\tilde{\varvec{u}}}\right) _i - \left( Q(\tilde{\varvec{\omega }}\times {\tilde{\varvec{u}}}) \right) _i \nonumber \\& \qquad-(\partial _t X\cdot J_Y^T \nabla )(Q{\tilde{\varvec{u}}})_i - \left( (Q{\tilde{\varvec{u}}})\cdot (J_Y^T\nabla )\right) (Q{\tilde{\varvec{u}}})_i \nonumber \\& \qquad+ \sum _{m,l,j} \frac{\partial (Q{\tilde{\varvec{u}}})_i}{\partial y_l} \frac{\partial Y_m}{\partial x_j} \frac{\partial }{\partial y_m}\left( \frac{\partial Y_l}{\partial x_j}\right) \nonumber \\& \qquad+ \sum _{m,l,j}\frac{\partial ^2 (Q{\tilde{\varvec{u}}})_i}{\partial y_m \partial y_l} \frac{\partial Y_l}{\partial x_j} \frac{\partial Y_m}{\partial x_j} -\Delta {\tilde{\varvec{u}}} _i\nonumber \\& \qquad+\left( (I_3 -J^T_Y)\nabla {\tilde{\pi }}\right) _i ; \end{aligned}$$

(7.8)

$$\begin{aligned}&{\mathcal {G}}({\tilde{\varvec{u}}}, \tilde{\varvec{l}}, \tilde{\varvec{\omega }}) := \nabla {\tilde{\varvec{u}}}: (I_3 - (J_Y Q)^T) = {\mathrm {div}}\ \varvec{H} \quad \text { with } \quad \varvec{H}({\tilde{\varvec{u}}}, \tilde{\varvec{h}}, \tilde{\varvec{\omega }}) := (I_3-J_YQ) \tilde{\varvec{u}} ; \end{aligned}$$

(7.9)

$$\begin{aligned}&\varvec{F}_1(\tilde{\varvec{l}},\tilde{\varvec{\omega }}) := -m \tilde{\varvec{\omega }} \times \tilde{\varvec{l}} ; \end{aligned}$$

(7.10)

$$\begin{aligned}&\varvec{F}_2(\tilde{\varvec{\omega }}) := {\tilde{J}} \tilde{\varvec{\omega }}\times \tilde{\varvec{\omega }}. \end{aligned}$$

(7.11)

Note that a solution $({\tilde{\varvec{u}}},{\tilde{\pi }},\tilde{\varvec{l}},\tilde{\varvec{\omega }})$ to (7.7) yields a solution $(\varvec{u},\pi ,\varvec{l},\varvec{\omega })$ to (2.1) by (7.5).