Skip to main content
SpringerLink
Log in

Holomorphic Relative Hopf Modules over the Irreducible Quantum Flag Manifolds

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

A Correction to this article was published on 19 February 2021

This article has been updated

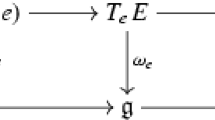
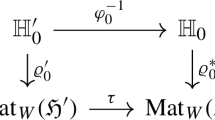Abstract

We construct covariant q-deformed holomorphic structures for all finitely generated relative Hopf modules over the irreducible quantum flag manifolds endowed with their Heckenberger–Kolb calculi. In the classical limit, these reduce to modules of sections of holomorphic homogeneous vector bundles over irreducible flag manifolds. For the case of simple relative Hopf modules, we show that this covariant holomorphic structure is unique. This generalises earlier work of Majid, Khalkhali, Landi, and van Suijlekom for line modules of the Podleś sphere, and subsequent work of Khalkhali and Moatadelro for general quantum projective space.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Change history

References

  1. Baston, R.J., Eastwood, M.G.: The Penrose transform. Its interaction with representation theory, Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York (1989). Oxford Science Publications

  2. Beggs, E., Majid, S.: Spectral triples from bimodule connections and Chern connections. J. Noncommut. Geom. 11, 669–701 (2017)

    Article  MathSciNet  Google Scholar 

  3. Beggs, E., Majid, S.: Quantum Riemannian Geometry, vol. 355 of Grundlehren der mathematischen Wissenschaften, Springer International Publishing, 1 ed. (2019)

  4. Beggs, E., Smith, P.S.: Noncommutative complex differential geometry. J. Geom. Phys. 72, 7–33 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  5. Böhm, G., Brzeziński, T.: Strong connections and the relative Chern–Galois character for corings, Int. Math. Res. Not., pp. 2579–2625 (2005)

  6. Bott, R.: Homogeneous vector bundles. Ann. Math 66(2), 203–248 (1957)

    Article  MathSciNet  Google Scholar 

  7. Brzeziński, T., Hajac, P.M.: The Chern–Galois character. C. R. Math. Acad. Sci. Paris 338, 113–116 (2004)

    Article  MathSciNet  Google Scholar 

  8. Brzeziński, T., Janelidze, G.J., Maszczyk, T.: Galois structures, in Lecture notes on noncommutative geometry and quantum groups, P. M. Hajac, ed. (2008) Available at http://www.mimuw.edu.pl/~pwit/ toknotes/toknotes.pdf

  9. Brzeziński, T., Majid, S.: Quantum geometry of algebra factorisations and coalgebra bundles. Commun. Math. Phys. 213, 491–521 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  10. Chari, V., Pressley, A.: A Guide to Quantum Groups. Cambridge University Press, Cambridge (1994)

    MATH  Google Scholar 

  11. Connes, A., Moscovici, H.: The local index formula in noncommutative geometry. Geom. Funct. Anal. 5, 174–243 (1995)

    Article  MathSciNet  Google Scholar 

  12. D’Andrea, F., Da̧browski, L.: Dirac operators on quantum projective spaces. Commun. Math. Phys 295, 731–790 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  13. Das, B., Ó Buachalla, R., Somberg, P.: Dolbeault–Dirac Fredholm operators on quantum homogeneous spaces. arXiv:1910.14007

  14. García, F. Díaz, Krutov, A., Ó Buachalla, R., Somberg, P., Strung, K.R.: Positive line bundles over the irreducible quantum flag manifolds. arXiv:1912.08802

  15. García, F. Díaz, Ó Buachalla, R., Wagner, E.: A Borel–Weil theorem for the irreducible quantum flag manifolds. In preparation

  16. Drinfeld, V.G.: Quantum groups, in Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Berkeley, Calif., 1986), Am. Math. Soc., Providence, RI, pp. 798–820 (1987)

  17. Heckenberger, I., Kolb, S.: The locally finite part of the dual coalgebra of quantized irreducible flag manifolds. Proc. London Math. Soc 89(3), 457–484 (2004)

    Article  MathSciNet  Google Scholar 

  18. Heckenberger, I., Kolb, S.: De Rham complex for quantized irreducible flag manifolds. J. Algebra, 305, pp. 704–741 (2006)

  19. Helgason, S.: Differential geometry, Lie groups, and symmetric spaces, vol. 80 of Pure and Applied Mathematics, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York (1978)

  20. Huybrechts, D.: Complex Geometry: An Introduction, Universitext. Springer, Berlin (2005)

    MATH  Google Scholar 

  21. Jimbo, M.: A \(q\)-analogue of \(U(\mathfrak{gl}(N+1))\), Hecke algebra, and the Yang-Baxter equation. Lett. Math. Phys. 11, 247–252 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  22. Khalkhali, M., Landi, G., van Suijlekom, W.D.: Holomorphic structures on the quantum projective line, Int. Math. Res. Not. IMRN, pp. 851–884 (2011)

  23. Khalkhali, M., Moatadelro, A.: Noncommutative complex geometry of the quantum projective space. J. Geom. Phys. 61, 2436–2452 (2011)

    Article  ADS  MathSciNet  Google Scholar 

  24. Klimyk, A., Schmüdgen, K.: Quantum Groups and Their Representations, Texts and Monographs in Physics, Springer, Berlin (1997)

  25. Koszul, J.-L., Malgrange, B.: Sur certaines structures fibrées complexes. Arch. Math. (Basel) 9, 102–109 (1958)

    Article  MathSciNet  Google Scholar 

  26. Majid, S.: A quantum groups primer. London Mathematical Society Lecture Note Series, vol. 292. Cambridge University Press, Cambridge (2002)

  27. Majid, S.: Noncommutative Riemannian and spin geometry of the standard \(q\)-sphere, Commun. Math. Phys., 256, pp. 255–285 (2005)

  28. Matassa, M.: Kähler structures on quantum irreducible flag manifolds. J. Geom. Phys. 145, 103477 (2019)

    Article  MathSciNet  Google Scholar 

  29. Mrozinski, C., Ó Buachalla, R.: A Borel–Weil theorem for the quantum Grassmannians. arXiv:1611.07969

  30. Müller, E.F., Schneider, H.-J.: Quantum homogeneous spaces with faithfully flat module structures. Israel J. Math. 111, 157–190 (1999)

    Article  MathSciNet  Google Scholar 

  31. Ó Buachalla, R.: Noncommutative complex structures on quantum homogeneous spaces. J. Geom. Phys. 99, 154–173 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  32. Ó Buachalla, R.: Noncommutative Kähler structures on quantum homogeneous spaces, Adv. Math., 322, pp. 892–939 (2017)

  33. Ó Buachalla, R., Šťoviček, J., van Roosmalen, A.-C.: A Kodaira vanishing theorem for noncommutative Kähler structures. arXiv:1801.08125 (2018)

  34. Polishchuk, A.: Classification of holomorphic vector bundles on noncommutative two-tori. Doc. Math. 9, 163–181 (2004)

    MathSciNet  MATH  Google Scholar 

  35. Polishchuk, A., Schwarz, A.: Categories of holomorphic vector bundles on noncommutative two-tori. Commun. Math. Phys. 236, 135–159 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  36. Schauenburg, P., Schneider, H.-J.: On generalized Hopf Galois extensions. J. Pure Appl. Algebra 202, 168–194 (2005)

    Article  MathSciNet  Google Scholar 

  37. Serre, J.-P.: Représentations linéaires et espaces homogènes kählériens des groupes de Lie compacts (d’après Armand Borel et André Weil), in Séminaire Bourbaki, Vol. 2, Soc. Math. France, Paris, 1995, pp. 447–454

  38. Takeuchi, M.: Relative Hopf modules–equivalences and freeness criteria. J. Algebra 60, 452–471 (1979)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centro de Ciencias Matemáticas, Universidad Nacional Autónoma de México, Antigua Carretera a Pátzcuaro 8701 Col. Ex Hacienda San José de la Huerta, C.P. 58089, Morelia, Mexico

    Fredy Díaz García

  2. Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000, Zagreb, Croatia

    Andrey Krutov

  3. Institute of Mathematics, Czech Academy of Sciences, Žitná 25, 115 67, Prague, Czech Republic

    Andrey Krutov & Karen R. Strung

  4. Independent University of Moscow, Bolshoj Vlasyevskij Per. 11, 119002, Moscow, Russia

    Andrey Krutov

  5. Département de Mathématiques, Faculté des sciences, Université Libre de Bruxelles, Boulevard du Triomphe, B-1050, Bruxells, Belgium

    Réamonn Ó Buachalla

  6. Mathematical Institute of Charles University, Sokolovská 83, 186 75, Prague, Czech Republic

    Réamonn Ó Buachalla & Petr Somberg

Authors
  1. Fredy Díaz García
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrey Krutov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Réamonn Ó Buachalla
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Petr Somberg
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Karen R. Strung
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Réamonn Ó Buachalla.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

FDG is partially funded by Conacyt (Consejo Nacional de Ciencia y Tecnología, México). AK was supported by the QuantiXLie Centre of Excellence, a project cofinanced by the Croatian Government and European Union through the European Regional Development Fund — the Competitiveness and Cohesion Operational Programme (KK.01.1.1.01.0004). RÓB acknowledges FNRS support through a postdoctoral fellowship within the framework of the MIS Grant “Antipode” grant number F.4502.18. RÓB and PS are partially supported from the Eduard Čech Institute within the framework of the grant GAČR \(19-28628X\), and by the grant GA19-06357S. Research of KRS and AK is supported by the GAČR project 20-17488Y and RVO: 67985840.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Díaz García, F., Krutov, A., Ó Buachalla, R. et al. Holomorphic Relative Hopf Modules over the Irreducible Quantum Flag Manifolds. Lett Math Phys 111, 10 (2021). https://doi.org/10.1007/s11005-020-01340-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11005-020-01340-7

Keywords

Mathematics Subject Classification

Search

Navigation