Abstract
We investigate rate-independent stress paths under constant rate of strain within the hypoplasticity theory of Kolymbas type. For a particular simplified hypoplastic constitutive model, the exact solution of the corresponding system of nonlinear ordinary differential equations is obtained in analytical form. On its basis, the behaviour of stress paths is examined in dependence of the direction of the proportional strain paths and material parameters of the model.
Similar content being viewed by others
1 Introduction
The constitutive stress–strain relation for hypoplastic granular materials like cohesionless soil or broken rock is under our consideration. The respective constitutive law is of the rate type, incrementally nonlinear, and it is based on the hypoplastic concept proposed by Kolymbas [29]. Compared to incrementally linear constitutive equations, e.g. for hyperelastic and hypoelastic material laws, the hypoplastic constitutive equations are not differentiable at zero strain rate. This is due to different stiffnesses for loading and unloading typical for inelastic materials. In contrast to the classical elastoplastic concept, the strain in the theory of hypoplasticity is not decomposed into elastic and plastic parts. Detailed discussions about physical aspects of hypoplastic models can be found, for instance, in [20, 31, 36]; their response to cycling loading is studied in [9, 41], shear localization in [7, 10, 16, 23], critical states in [4, 5, 49], behaviour under undrained condition in [37], extension to a micropolar continuum in [23, 24], and thermodynamic aspects in [26, 42, 43].
Other typical representatives for incrementally nonlinear constitutive equations are, for instance, the Armstrong–Frederick model [2], the endochronic model by Valanis [45], the octolinear model by Darve [14, 15], the CLoE model by Chambon et al. [12], and the barodesy model by Kolymbas [30]. For variational approaches to modelling granular and multiphase media, we refer to [1, 27, 33].
Experiments with granular materials show a typical behaviour of the stress path obtained under a monotonic proportional deformation path which was formulated in two rules by Goldscheider [18]. The first rule says that a proportional deformation path starting from a nearly stress-free state results in a proportional stress path. The second rule says that a proportional deformation path starting from an arbitrary stress state asymptotically converges to the same proportional stress path as the one obtained for the initially stress-free state. These asymptotic properties of granular materials can be interpreted by fading memory of the material [21]. This feature is also confirmed by further experiments, e.g. [13, 44], and numerical simulations by the discrete element method, e.g. [25, 34].
As the asymptotic behaviour of the stress path for proportional deformation is an intrinsic property of granular materials, it has also great importance for constitutive models relevant to frictional granular materials. It can be noted that in many constitutive models the asymptotic behaviour is only fulfilled for particular deformation paths. The lack of this property can lead to large deviation of the prediction of stress paths not used for calibration.
In constitutive modelling, the asymptotic property is the starting point for barodesy modelling in [38], and it is also an intrinsic feature in hypoplasticity [20, 22, 28, 35, 36, 40]. With respect to a particular hypoplastic model by Kolymbas [28], stress paths were numerically investigated for initially axisymmetric stress states and axisymmetric proportional deformations. However, no general requirements for the asymptotic behaviour were formulated. A mathematical criterion providing a necessary condition for convergent asymptotic behaviour in incremental models was given first by Niemunis [40]. It requires that the normal distance of the generated stress path to the asymptote decreases with an increase in monotonic deformation, where the asymptote is obtained for the corresponding fixed strain rate starting from the initially stress-free state. The criterion by Niemunis is applicable to all rate-type models; however, it is restricted to proportional deformation paths with contractant volume strain behaviour.
In the present paper, a different strategy is proposed to examine the asymptotic behaviour using the analytical solution for the stress path, which depends on the direction of the proportional strain path, the initial stress state, and the material parameters involved in the constitutive equation. The main challenge in developing proper mathematical tools is the strongly nonlinear character of the underlying differential equations. Following the rate-independent technique developed in [11], we gave a rigorous mathematical proof of the existence of asymptotic states in [8, 32]. This idea is further developed in the present work.
To this end, a simplified version of the hypoplastic model by Gudehus [19] and Bauer [3] is considered. For the sake of simplicity, the pressure- and density-dependent properties of granular materials described in [3, 19] are omitted so that only two material parameters remain in the model. It can be noted that the same simplified version can also be obtained from the hypoplastic model by von Wolffersdorff [46] as shown in [6].
For the simplified hypoplastic model, we construct the solution of the corresponding nonlinear problem in a closed form. In this way, we make also a close link to barodesy models [30]. The exact solution allows us to describe analytically various scenarios of the behaviour of stress paths obtained from monotonic compression, extension, and isochoric deformations. The latter leads to stress limit states or the so-called critical stress states, which can be represented by a conical surface in the space of principal stresses. In particular, we identify the domain of the constitutive parameters which guarantee that for proportional deformation paths the corresponding stress paths starting from an arbitrary initial stress state are asymptotically stable.
2 The model
We first fix some basic tensor notation. By \({\mathbb {R}}^{3\times 3}_\mathrm{sym}\), we denote the space of symmetric 3-by-3 tensors of second-order  and
and  , which are endowed with the usual double dot product, the associated norm, and the trace, respectively:
, which are endowed with the usual double dot product, the associated norm, and the trace, respectively:

Here,  stands for the 3-by-3 identity matrix with the Kronecker symbol \(\delta _{ij}=1\) for \(i=j\), and zero otherwise. In physical interpretation,
stands for the 3-by-3 identity matrix with the Kronecker symbol \(\delta _{ij}=1\) for \(i=j\), and zero otherwise. In physical interpretation,  corresponds to the Cauchy stress tensor, and
corresponds to the Cauchy stress tensor, and  is the strain rate tensor. For time \(t\ge 0\), we interpret
is the strain rate tensor. For time \(t\ge 0\), we interpret  and
and  as time-dependent tensor-valued functions.
as time-dependent tensor-valued functions.
With respect to the normalized stress tensor  , the general representation of the hypoplastic constitutive equation of the Kolymbas type can be written in the factorized form as the following tensor equation for the objective stress rate:
, the general representation of the hypoplastic constitutive equation of the Kolymbas type can be written in the factorized form as the following tensor equation for the objective stress rate:

where  is a symmetric second-order tensor,
is a symmetric second-order tensor,  is a symmetric fourth-order tensor, and the double dot product is to be interpreted as
is a symmetric fourth-order tensor, and the double dot product is to be interpreted as

The dimensionless parameter \(c<0\) scales the incremental stiffness and can be calibrated, for instance, based on an isotropic compression test. The right-hand side of (1.1) is a homogeneous function of degree one in  . Note that dry granular materials are cohesionless, so that only negative principal stresses are relevant to the constitutive equation (1.1). Furthermore, we remark that particular representations of the tensor functions in (1.1) are based on terms from the general representation theorem of isotropic tensor-valued functions [47]. Various explicit versions are proposed in the literature (e.g. [3, 19, 29, 43, 48, 49]). In this paper, we consider a particular version of (1.1) proposed by Bauer in [5] in a simplified manner:
. Note that dry granular materials are cohesionless, so that only negative principal stresses are relevant to the constitutive equation (1.1). Furthermore, we remark that particular representations of the tensor functions in (1.1) are based on terms from the general representation theorem of isotropic tensor-valued functions [47]. Various explicit versions are proposed in the literature (e.g. [3, 19, 29, 43, 48, 49]). In this paper, we consider a particular version of (1.1) proposed by Bauer in [5] in a simplified manner:

with the normalized stress deviator  /3, where the symbol
/3, where the symbol  stands for the fourth-order identity tensor, the symbol \(\otimes \) denotes the dyadic product of tensors, and the term in (1.1) which is linear in
stands for the fourth-order identity tensor, the symbol \(\otimes \) denotes the dyadic product of tensors, and the term in (1.1) which is linear in  can also be represented as:
can also be represented as:

The constitutive constant \(a>0\) is called limit stress state parameter and characterizes the shape of the conical limit stress surface or the so-called critical stress state surface in the principal stress space [5]. Critical states are defined for a vanishing stress rate under continuous isochoric deformation. For critical stress states, parameter a equals the norm of the normalized stress deviator, i.e.  , and it can be related to the so-called critical friction angle [4]. While in the model by Gudehus [19] and Bauer [3] the value of a also depends on the orientation of the stress deviator, parameter a is assumed to be a constant in the present paper. For the granular friction angle \(\phi \in (0,\pi / 2)\) such that \(a =2\sqrt{2/3}\sin \phi / (3 -\sin \phi )\), we get the physical restriction \(a <a_\mathrm{phys}=\sqrt{2/3}\approx 0.8165\) as \(\sin \phi < 1\).
, and it can be related to the so-called critical friction angle [4]. While in the model by Gudehus [19] and Bauer [3] the value of a also depends on the orientation of the stress deviator, parameter a is assumed to be a constant in the present paper. For the granular friction angle \(\phi \in (0,\pi / 2)\) such that \(a =2\sqrt{2/3}\sin \phi / (3 -\sin \phi )\), we get the physical restriction \(a <a_\mathrm{phys}=\sqrt{2/3}\approx 0.8165\) as \(\sin \phi < 1\).
3 Hypoplastic model under proportional deformation
Further we restrict ourselves to strain paths pointing in one fixed direction. Namely, we call a strain path proportional if there exists a time-independent symmetric second-order tensor  normalized by
normalized by  and a scalar time-dependent function s(t) with \(s(0) =0\) and \( \dot{s}(t)>0\) such that it holds
and a scalar time-dependent function s(t) with \(s(0) =0\) and \( \dot{s}(t)>0\) such that it holds

In (2.1),  determines a prescribed direction in the space of symmetric second-order tensors, and s represents a monotonic increasing parameter. Moreover, we assume deformations for which the objective time derivative and the material time derivative coincide, i.e.
determines a prescribed direction in the space of symmetric second-order tensors, and s represents a monotonic increasing parameter. Moreover, we assume deformations for which the objective time derivative and the material time derivative coincide, i.e.  , which, for example, holds for fixed directions of principal stresses. As the material behaviour described by Eq. (1) is isotropic, the strain rate tensor with fixed principal values, i.e. the strain increments are proportional and coaxial, corresponds to a stress rate tensor
, which, for example, holds for fixed directions of principal stresses. As the material behaviour described by Eq. (1) is isotropic, the strain rate tensor with fixed principal values, i.e. the strain increments are proportional and coaxial, corresponds to a stress rate tensor  with zero elements outside the diagonal. Thus, the relevant system of ordinary differential equations (ODE) reduces to three.
with zero elements outside the diagonal. Thus, the relevant system of ordinary differential equations (ODE) reduces to three.
In this case, inserting the chain rule \(\mathrm{d}/\mathrm{d}t = \dot{s} \mathrm{d}/\mathrm{d}s\) and  according to (2.1) and dividing with \(\dot{s}\not =0\), we can rewrite the rate-independent relations (1) with respect to \(s>0\) in the form:
according to (2.1) and dividing with \(\dot{s}\not =0\), we can rewrite the rate-independent relations (1) with respect to \(s>0\) in the form:

or, equivalently, without factorization:

where the formula  was used, and
was used, and

In the principal stress space, the representation of the normalized quantity  indicates the direction of the asymptotic stress state for \(s \rightarrow \infty \). This observation will be specified below after the representation formula (5.6). Indeed, formula (5.6.1) shows that the evolution of
indicates the direction of the asymptotic stress state for \(s \rightarrow \infty \). This observation will be specified below after the representation formula (5.6). Indeed, formula (5.6.1) shows that the evolution of  takes place in the 2D plane generated by constant tensors
takes place in the 2D plane generated by constant tensors  and
and  . We shall see that the scalar coefficient of
. We shall see that the scalar coefficient of  is dominant and determines the asymptotic convergence or divergence of the stress path as \(s \rightarrow \infty \).
is dominant and determines the asymptotic convergence or divergence of the stress path as \(s \rightarrow \infty \).
In system (2.3) of ordinary differential equations (ODE) for  , the last term in the right-hand side is nonlinear in
, the last term in the right-hand side is nonlinear in  . For (2.3), we prescribe the initial condition at \(s=0\):
. For (2.3), we prescribe the initial condition at \(s=0\):

where  is a given initial stress tensor.
is a given initial stress tensor.
In the following, we study the behaviour as \(s\rightarrow \infty \) of solutions  to the nonlinear initial value problem (2) in dependence of the direction
to the nonlinear initial value problem (2) in dependence of the direction  of proportional strain paths, the material parameter a, and the initial stress
of proportional strain paths, the material parameter a, and the initial stress  .
.
3.1 Motivating example: isotropic compression/extension
In this Section an assembly of grains with a grain skeleton is considered under compressive stresses. In mathematical terms, it means that all principal stress components are negative. Here, by compression or extension we mean the dynamics of the process defined by (2.1), where the strain rate can be, respectively, negative or positive.
(i) Isotropic compression: Under a monotonic displacement controlled isotropic compression, we understand the situation of Eq. (2.3) corresponding to the choice  . Then
. Then  can easily be found as the solution of the linear scalar equation
can easily be found as the solution of the linear scalar equation

that is,

Since the model is valid only for compressive stresses, we necessarily have  . Furthermore, \(c<0\) and \(D^- <0\), so that the negative stress trace exponentially grows when the compression linearly increases along the direction of
. Furthermore, \(c<0\) and \(D^- <0\), so that the negative stress trace exponentially grows when the compression linearly increases along the direction of  for all \(a>0\). Equation (2.3) turns into the form
for all \(a>0\). Equation (2.3) turns into the form

In view of (3.2), the solution of (3.3) reads

If the deviator  of the initial stress is zero, that is, the initial stress is located on the isotropic axis generated by
of the initial stress is zero, that is, the initial stress is located on the isotropic axis generated by  , then the whole stress path lies on the isotropic axis. Otherwise, if the initial stress deviator does not vanish, there are three possible scenarios for the evolution of
, then the whole stress path lies on the isotropic axis. Otherwise, if the initial stress deviator does not vanish, there are three possible scenarios for the evolution of  depending on whether \(E^->0\), \(E^- < 0\), or \(E^- =0\).
depending on whether \(E^->0\), \(E^- < 0\), or \(E^- =0\).
Scenario (a) If \(E^- > 0\), then we have \(cE^- < 0\), and the stress path converges exponentially to the isotropic trajectory with increasing time, so that the model is exponentially stable with respect to small perturbations of the initial stress.
Scenario (b) The situation is totally different when \(E^- < 0\). Then \(cE^- > 0\), and small perturbations of the initial stress produce exponentially large deviation of the stress path from the isotropic trajectory.
Scenario (c) In the limit case \(E^- = 0\), the distance of the solution trajectory from the isotropic axis remains constant.
Thus, scenarios (b) and (c) do not fulfil the second law by Goldscheider. According to the sign of \(E^-\) in (3.3) we see that for the stability of the model with respect to variations of the initial stress (scenario (a)) it needs \(a>a_{\min }\), and the critical parameter value is \(a_{\min } = 1/(2\sqrt{3})\approx 0.2887\). For smaller values of a (scenario (b)), we are in the classical philosophical situationFootnote 1 described by Frank Brentano.
For illustration, in Fig. 1 we show the projection of the stress paths onto the so-called Rendulic plane for particular values \(a=0.1\), \(a=a_{\min }\), and \(a=1\), and an initial stress  . We observe that: for \(a=1>a_{\min }\) (solid curve) according to scenario (a) the stress paths tend towards the isotropic axis (dot dashed line), which is, in this case, the asymptote; for \(a=0.1 <a_{\min }\) (dashed curve), there is no asymptotic behaviour implying scenario (b); and for \(a=a_{\min }\) (dotted curve), the stress path is parallel to the isotropic axis implying scenario (c).
. We observe that: for \(a=1>a_{\min }\) (solid curve) according to scenario (a) the stress paths tend towards the isotropic axis (dot dashed line), which is, in this case, the asymptote; for \(a=0.1 <a_{\min }\) (dashed curve), there is no asymptotic behaviour implying scenario (b); and for \(a=a_{\min }\) (dotted curve), the stress path is parallel to the isotropic axis implying scenario (c).
(ii) Isotropic extension: For an initially prestressed state of monotonic isotropic extension, we have  resulting in the equations for
resulting in the equations for  :
:

and, respectively, for  :
:

As given above, its solution can be written in the form

In this case, we have \(D^+ >0\) and \(E^+ > 0\), and the stress \(\sigma (s)\) in (4.3) decays exponentially to zero as \(s\rightarrow \infty \) independently of the choice of the initial condition.
We remark that according to the derived formulas (3) and (4) (as well as in the general case (2.3)) the parameter \(c<0\) does affect neither the asymptotic states nor the shape of stress paths; rather, it influences how quick a proportional stress path is approached.
Motivated by this special example, it is our aim to investigate in the following the stress path under general proportional deformations.
3.2 Analytical solution of the hypoplastic equation for general proportional deformations
The principal difficulty of solving the ODE (2.3) in the general form is its non-linearity in the stress. Here, we apply the following procedure consisting of three steps:
- Step 1:
We derive from (2.3) an ODE for the auxiliary scalar variable
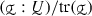 and find its solution;
and find its solution;- Step 2:
Inserting the solution to Eq. (2.3) projected in the isotropic direction, we obtain a linear equation for
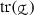 and solve it;
and solve it;- Step 3:
Substituting this solution in the constitutive relation (2.3), we find an expression of
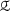 in the closed form.
in the closed form.
A rigorous derivation of the analytical solution is given in the “Appendix.” Below we summarize the resulting formulas and discuss similarities between hypoplasticity and barodesy models.
Let  be as in (2.4) and assume
be as in (2.4) and assume  . To simplify the formulas, we introduce the constants (see (17.1) and (17.6))
. To simplify the formulas, we introduce the constants (see (17.1) and (17.6))

and the function h(s) with \(h(0) =0\) and depending on the initial stress tensor  , defined by the formula (see (16.4) and (17.3)):
, defined by the formula (see (16.4) and (17.3)):

In (17.1), we prove that the differential equation (2.3) can be transformed into the following equation:

It is worth noting that (5.3) has the structure (up to a factorization) of a constitutive relation adopted in barodesy; see, for example, [38]:

where  is a given direction of the proportional stress path and \({\mathfrak {f}}\) and \({\mathfrak {g}}\) are model parameters. The exponential expression of
is a given direction of the proportional stress path and \({\mathfrak {f}}\) and \({\mathfrak {g}}\) are model parameters. The exponential expression of  is formal and admits the expansion in \(-\alpha \):
is formal and admits the expansion in \(-\alpha \):

The first two linear asymptotic terms in (5.5) with \(\alpha =-3a\) yield exactly  in (2.4), and the nonlinear behaviour of
in (2.4), and the nonlinear behaviour of  with respect to
with respect to  is substituted in the Kolymbas-type hypoplastic model by the norm
is substituted in the Kolymbas-type hypoplastic model by the norm  (which is normalized to one here). In this context, it can be mentioned that with constant a Eq. (1) models the stress limit condition by Drucker–Prager. For a refined modelling of the stress limit condition for granular materials, factor a should depend on the orientation of the stress deviator, i.e. it should be a function of the so-called Lode angle, which allows the adaptation of arbitrary conically shaped stress limit conditions in the principal stress space as outlined in [3, 4]. Taking into account the contribution
(which is normalized to one here). In this context, it can be mentioned that with constant a Eq. (1) models the stress limit condition by Drucker–Prager. For a refined modelling of the stress limit condition for granular materials, factor a should depend on the orientation of the stress deviator, i.e. it should be a function of the so-called Lode angle, which allows the adaptation of arbitrary conically shaped stress limit conditions in the principal stress space as outlined in [3, 4]. Taking into account the contribution  in Eq. (5.5), the barodesy model describes a stress limit condition close to the one by Matsuoka–Nakai [39] as shown in [17, 38]. In hypoplasticity, the stress limit condition by Matsuoka–Nakai can be predefined as shown, for instance, in [4, 46]. In both models (barodesy and hypoplasticity), parameters \(\alpha \) and a are related to the granular friction angle.
in Eq. (5.5), the barodesy model describes a stress limit condition close to the one by Matsuoka–Nakai [39] as shown in [17, 38]. In hypoplasticity, the stress limit condition by Matsuoka–Nakai can be predefined as shown, for instance, in [4, 46]. In both models (barodesy and hypoplasticity), parameters \(\alpha \) and a are related to the granular friction angle.
Based on the representation (5.3) which is linear in  , the solution of the initial value problem (2) can be found in the closed form (see (18.3)):
, the solution of the initial value problem (2) can be found in the closed form (see (18.3)):

with E and D defined as in (5.1), h(s) as in (5.2), and  as in (2.4), whereas
as in (2.4), whereas  . For the special case
. For the special case  , that is,
, that is,  for \(a\not =0\), see formulas (19). Due to
for \(a\not =0\), see formulas (19). Due to  , from (5.6) we compute
, from (5.6) we compute  and the normalized stress tensor
and the normalized stress tensor

Therefore, \(D-E<0\) in (5.7) proves the asymptotic convergence

exponentially as \(s \rightarrow \infty \).
Since only negative principal stresses are relevant for the underlying model, it is important to discuss their feasibility. For this reason, we define the feasible cone:

where \(\sigma _1\), \(\sigma _2\), and \(\sigma _3\) are eigenvalues of  . Note that
. Note that  . Therefore, if \(E\ge D\), then \(\exp (c E s) \le \exp (c D s)\) (noting that \(c<0\)), so that rearranging the terms in Eq. (5.6) equivalently as
. Therefore, if \(E\ge D\), then \(\exp (c E s) \le \exp (c D s)\) (noting that \(c<0\)), so that rearranging the terms in Eq. (5.6) equivalently as

the factors in front of  and
and  are positive. Assuming that
are positive. Assuming that  and choosing the initial stress state
and choosing the initial stress state  thus guarantee that the whole stress path
thus guarantee that the whole stress path  is contained in \({\mathcal {K}}_\mathrm{f}\) for all \(s>0\). The detailed investigation of necessary and sufficient conditions on a and
is contained in \({\mathcal {K}}_\mathrm{f}\) for all \(s>0\). The detailed investigation of necessary and sufficient conditions on a and  to ensure that
to ensure that  reached by (2.4) lies in \({\mathcal {K}}_\mathrm{f}\) is the subject of the forthcoming research.
reached by (2.4) lies in \({\mathcal {K}}_\mathrm{f}\) is the subject of the forthcoming research.
In the next Sections, we investigate the asymptotic behaviour as \(s\rightarrow \infty \) of stress paths (5.6) in dependence of specific deformations  .
.
4 Asymptotic behaviour of stress paths under various proportional deformations
Similarly to the motivation example, we should distinguish contractant (volume-decreasing) from dilatant (volume-increasing) states. For this task, we call by contractant the compression corresponding to  , and by dilatant the extension when
, and by dilatant the extension when  , while
, while  corresponds to the volume-preserving deformation.
corresponds to the volume-preserving deformation.
To this end, we note that paths with  will eventually approach the origin as they are proportional volume-increasing deformation paths. However, there are examples of axial loading paths, e.g.
will eventually approach the origin as they are proportional volume-increasing deformation paths. However, there are examples of axial loading paths, e.g.  , with
, with  . Mašín [34] also observed with discrete element method simulations the so-called asymptotic extension states, that are obtained by
. Mašín [34] also observed with discrete element method simulations the so-called asymptotic extension states, that are obtained by  with axial loading.
with axial loading.
(i) Contractant straining: Let a tensor  be prescribed such that
be prescribed such that  . Recalling
. Recalling  , we have
, we have  for all \(a>0\). According to (5.2), it follows
for all \(a>0\). According to (5.2), it follows  and the finite limit (see Fig. 2 the left plot):
and the finite limit (see Fig. 2 the left plot):

From (5.1), we infer \(D^- <0\); hence, the second term in the right-hand side of (5.6) grows exponentially along  . The asymptotic behaviour of the first term depends on the sign of \(E^-\): it grows to plus or minus infinity if \(E^-<0\) and decays to a finite number if \(E^- =0\) and to zero if \(E^- >0\). The latter case corresponds to the proportional contractant deformation such that:
. The asymptotic behaviour of the first term depends on the sign of \(E^-\): it grows to plus or minus infinity if \(E^-<0\) and decays to a finite number if \(E^- =0\) and to zero if \(E^- >0\). The latter case corresponds to the proportional contractant deformation such that:

This condition is equal to

and describes the asymptotically stable stress path  in (5.6) attracting the direction of
in (5.6) attracting the direction of  as \(s\rightarrow \infty \) by the mean of descent distance:
as \(s\rightarrow \infty \) by the mean of descent distance:

We remark that the decay of the distance in (7.3) holds only for sufficiently large values of s. For instance, the distance may increase in some interval \(s\in (0,s_0)\) with \(s_0>0\) satisfying \(c E^- s_0 +h^-(s_0) =0\), when \(c E^- <0\) and \(h^-(s_0) >0\) for \(C^-<0\) in (7.1).
(ii) Dilatant straining: Let  obey
obey  . We consider first the case of
. We consider first the case of  and similarly to (7.1) (see Fig. 2 the left plot) obtain
and similarly to (7.1) (see Fig. 2 the left plot) obtain

Therefore, the stable asymptotic behaviour under the proportional dilatant deformation is guaranteed by \(D^+ >0\) and \(E^+ >0\), that is:

or, equivalently,

then the stress path  in (5.6) decays asymptotically to zero:
in (5.6) decays asymptotically to zero:

By this, if \(E^+ >D^+\), then the stress path is closer to  ; otherwise, it is closer to
; otherwise, it is closer to  when the opposite inequality \(E^+ <D^+\) holds.
when the opposite inequality \(E^+ <D^+\) holds.
In the special case of  , that is,
, that is,  , from (19) we have
, from (19) we have

The asymptotic stability should be considered separately.
If  , then
, then  and follows the limit in (5.2) (see Fig. 2 the right plot):
and follows the limit in (5.2) (see Fig. 2 the right plot):

In this case, \(\exp (c E^+ s +h^+(s))\) and \(\exp (c D^+ s +h^+(s))\) entering the stress path  in (5.6) may obey various asymptotic behaviour in dependence of the sign of parameter \(C^+\) in (10.1) and the values of \(E^+\), \(D^+\) in (5.1). The asymptotically stable decay to zero of stress paths is described by the following two cases: either \(C^+ =0\) (hence, \(h^+(s)\equiv 0\)) and \(E^+ >0\), \(D^+ >0\), that is:
in (5.6) may obey various asymptotic behaviour in dependence of the sign of parameter \(C^+\) in (10.1) and the values of \(E^+\), \(D^+\) in (5.1). The asymptotically stable decay to zero of stress paths is described by the following two cases: either \(C^+ =0\) (hence, \(h^+(s)\equiv 0\)) and \(E^+ >0\), \(D^+ >0\), that is:

or \(h^+(s)\rightarrow -\infty \) provided by \(C^+ >0\):

In the both cases (10.2) and (10.3), the exponential convergence holds:

The non-monotone behaviour of  is admissible for dilatant, too.
is admissible for dilatant, too.
(iii) Volume-preserving deformation Consider a proportional deformation  with
with  ; then,
; then,  , \(E=a\), and \(D =0\) in (5.1); hence,
, \(E=a\), and \(D =0\) in (5.1); hence,

with  , and the limit:
, and the limit:

We note that the limit states  in (11.1) for all admissible directions
in (11.1) for all admissible directions  with
with  and initial stresses
and initial stresses  form the cone of the limit stress states with the apex in the origin of the space of principal stress axes. From (11.1), we find that
form the cone of the limit stress states with the apex in the origin of the space of principal stress axes. From (11.1), we find that  ; thus, the interaction of this cone with the deviator plane, i.e. the plane with
; thus, the interaction of this cone with the deviator plane, i.e. the plane with  (see [4]), is represented by the circle of radius a:
(see [4]), is represented by the circle of radius a:

The analysis of asymptotic behaviour of stress paths under various proportional deformations from Sect. 4 in dependence of the parameters is summarized for convenience in Table 1.
5 Discussion of the asymptotic results
In the following, we omit the superscripts \(-, +\) and study how the parameters D and E defined in (5.1) are connected with the choice of a and  . Indeed, from (2.4) we have
. Indeed, from (2.4) we have  ; hence,
; hence,  , and we get that D and E are only dependent on a and
, and we get that D and E are only dependent on a and  . We note that the range of
. We note that the range of  is limited by
is limited by  . To prove this, we considered
. To prove this, we considered  ; therefore,
; therefore,  becomes extreme if \(U_{ij}=0, i\ne j\), so only the entries on the diagonal of
becomes extreme if \(U_{ij}=0, i\ne j\), so only the entries on the diagonal of  are distinct from zero. With the arithmetic quadratic mean inequality, we get:
are distinct from zero. With the arithmetic quadratic mean inequality, we get:

and equality holds for \(U_{11}=U_{22}=U_{33}=1/\sqrt{3}\).
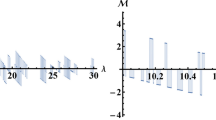
As we see in Table 1, the relations of D and E, one to each other and to zero, are crucial for the asymptotic behaviour of  as \(s\rightarrow \infty \). Depending on
as \(s\rightarrow \infty \). Depending on  (x-axis) and a (y-axis), these relations are plotted in Fig. 3.
(x-axis) and a (y-axis), these relations are plotted in Fig. 3.
Here, we consider the formal description of the plot, which means the equations of the curves separating the different greyscale areas, starting in the down left corner:
- –:
between area 1 and area 2:
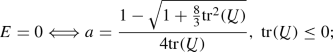
- –:
between area 2 and area 3:

- –:
between area 3 and area 4:
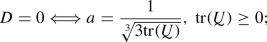
- –:
between area 4 and area 5:
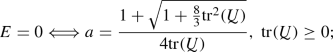
- –:
between area 5 and area 6:
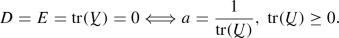
The meaning of the corresponding areas is the following:
- \(\square \):
in the light grey areas 2 and 4 (where parameters \(D<0<E\)), stress paths are going to infinity attracting
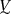 ;
;- \(\square \):
in the medium grey areas 1 and 5 (where \(D<E<0\)), stress paths do not have any asymptote and diverge;
- \(\square \):
in the dark grey area 3 (where \(0<D<E\)) stress paths go to zero attracting
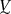 ;
;- \(\square \):
in the white area 6 (where \(0<E<D\)), the behaviour of the stress paths depends also on the initial stress state
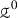 , while in the other areas the asymptotic behaviour is independent of the initial stress state.
, while in the other areas the asymptotic behaviour is independent of the initial stress state.
Further we illustrate the usage of Table 1 for the cases of contractant, dilatant, and volume-preserving deformations.
(i) Contractant straining
If  , the stress path is asymptotically stable in area 2. We get the lower bound for
, the stress path is asymptotically stable in area 2. We get the lower bound for  , which means isotropic compression, by
, which means isotropic compression, by
For \(a>a_{\min }\), we can be sure to have asymptotically stable behaviour for arbitrary proportional deformation (see Fig. 1 from Sect. 3.1).
(ii) Dilatant straining
If  , the stress path is asymptotically stable in areas 3 and 4: in area 3, the path tends to zero, while in area 4, it tends to infinity. We get the upper bound for
, the stress path is asymptotically stable in areas 3 and 4: in area 3, the path tends to zero, while in area 4, it tends to infinity. We get the upper bound for  , which means isotropic extension, by
, which means isotropic extension, by
For \(a<a_{\max }\), we have asymptotically stable behaviour for arbitrary proportional extension; in this case, the stress path will also tend to zero.
(iii) Volume-preserving deformation
For the limiting case of  , the stress path will tend to a certain stress state at the critical cone. To illustrate the matter, we plot few results of numerical simulation.
, the stress path will tend to a certain stress state at the critical cone. To illustrate the matter, we plot few results of numerical simulation.
In the left plot of Fig. 4, the stress paths are projected in the plane spanned by \(-\sigma _{33}\) and the first median of the \(-\sqrt{2}\sigma _{11}=-\sqrt{2}\sigma _{22}\)-plane. The dot dashed line is the isotropic axis; the outer solid lines are the intersection with the critical cone. In the right plot, the paths are projected onto the deviator stress plane  . In the deviator plane, the cutting line with the critical cone forms a circle of radius a according to (11.2). In Fig. 4, we see three example stress paths under volume-preserving deformation
. In the deviator plane, the cutting line with the critical cone forms a circle of radius a according to (11.2). In Fig. 4, we see three example stress paths under volume-preserving deformation  with the parameter \(a=0.35\) and three initial stress states
with the parameter \(a=0.35\) and three initial stress states

We can observe that for volume-preserving deformation all stress paths tend to the critical cone independent of the choice of  .
.
For comparison, in the similar coordinate axes as in Fig. 4, in Fig. 5 we see three stress paths starting at the initial stress state  with the parameter \(a=0.35\) under three different deformations
with the parameter \(a=0.35\) under three different deformations

We see that for different deformations  we get different behaviour of the stress paths. For
we get different behaviour of the stress paths. For  (solid curve), we have isotropic compression, and the corresponding stress path tends to the isotropic axis. For
(solid curve), we have isotropic compression, and the corresponding stress path tends to the isotropic axis. For  (dashed curve), we have uniaxial compression, and we can also observe an asymptotic behaviour. For
(dashed curve), we have uniaxial compression, and we can also observe an asymptotic behaviour. For  (dotted curve), we have volume-preserving deformation and the stress path goes to the critical cone.
(dotted curve), we have volume-preserving deformation and the stress path goes to the critical cone.
6 Case studies
In this Section, we will discuss the case of isotropic deformation and uniaxial deformation in more detail.
6.1 Isotropic deformation
(i) Compression: We can now give a more detailed interpretation of the results of Sect. 3.1. The contractant stress path (3.4) with \(D^- =-(3 a^3 +1/ \sqrt{3})/ (\sqrt{3}a +1)\), \(E^- = 2a - 1/ \sqrt{3}\) is exponentially stable along  for \(a >1/ (2\sqrt{3})\approx 0.2887\) and \(a<a_\mathrm{phys}\), and its distance from the
for \(a >1/ (2\sqrt{3})\approx 0.2887\) and \(a<a_\mathrm{phys}\), and its distance from the  -axis grows to infinity if \(a < 1/ (2\sqrt{3})\) and remains constant for \(a = 1/ (2\sqrt{3})\).
-axis grows to infinity if \(a < 1/ (2\sqrt{3})\) and remains constant for \(a = 1/ (2\sqrt{3})\).
(ii) Extension: In the dilatant case (4.3) with \(D^+ =\sqrt{3} a^2 + a + 1/ \sqrt{3}\), \(E^+ = 2a + 1/ \sqrt{3}\),  , the critical value is \(a_{\max } =1/ \sqrt{3} \approx 0.5774\). Then
, the critical value is \(a_{\max } =1/ \sqrt{3} \approx 0.5774\). Then  and similarly as in formulas (19.2) and (19.3) we obtain the solution
and similarly as in formulas (19.2) and (19.3) we obtain the solution  , which agrees with (4.3) for \(D^+ = E^+ =\sqrt{3}\). This corresponds to cases (8.2), (9), and (10.2), and from (4.3), we conclude unconditional asymptotic decay to zero:
, which agrees with (4.3) for \(D^+ = E^+ =\sqrt{3}\). This corresponds to cases (8.2), (9), and (10.2), and from (4.3), we conclude unconditional asymptotic decay to zero:

By this, if \(E^+ >D^+\), which holds for \(a<1/ \sqrt{3}\), then  attracts closer the direction of
attracts closer the direction of  . Otherwise,
. Otherwise,  is more attractive. The result in dependence on the parameter a is gathered for convenience in Table 2.
is more attractive. The result in dependence on the parameter a is gathered for convenience in Table 2.
We remark that this particular case of isotropic compression/extension implies \(\mu =D^\mp \) being the single eigenvalue and \(\mu =E^\mp \) the double eigenvalue for the following eigenvalue problem written with respect to \(\mu \), respectively:

where  stands for the 3-by-3 matrix of ones and
stands for the 3-by-3 matrix of ones and  is the eigenvector corresponding to \(D^\mp \); see [32] for details.
is the eigenvector corresponding to \(D^\mp \); see [32] for details.
6.2 Uniaxial deformation
(i) Asymptotic compression: We consider a so-called oedometric test, which is a uniaxial deformation under lateral zero strain, i.e.  , then
, then  ,
,  , and
, and  . Substituting it in (5.1) gives \(E^- =(2a^2 +a -1/3)/ (a+1)\), \(D^- =-(a^3 +1/3)/ (a+1) <0\), and in (5.2) provides:
. Substituting it in (5.1) gives \(E^- =(2a^2 +a -1/3)/ (a+1)\), \(D^- =-(a^3 +1/3)/ (a+1) <0\), and in (5.2) provides:

The condition (7.2) for \(E^- >0\) implying \(2a^2 +a -1/3 >0\) holds true if \(a >a_0 :=(\sqrt{11/3} -1)/ 4\approx 0.2287\); then, it provides the asymptotically stable stress path along the direction of  as described in (7.3), which is monotone if \(C^-\ge 0\). Otherwise, if \(0 <a \le a_0\), then the stress path grows to infinity.
as described in (7.3), which is monotone if \(C^-\ge 0\). Otherwise, if \(0 <a \le a_0\), then the stress path grows to infinity.
(ii) Asymptotic extension: For  and
and  such that
such that  , and
, and  , we calculate \(E^+ =(-2a^2 +a +1/3)/ (1 -a)\), \(D^+ =(a^3 -1/3)/ (1 -a)\), and
, we calculate \(E^+ =(-2a^2 +a +1/3)/ (1 -a)\), \(D^+ =(a^3 -1/3)/ (1 -a)\), and

Both conditions (8.2) are valid for \(a <a_1 :=1/ \root 3 \of {3} \approx 0.6934\) providing \(a^3 <1/3\), since \(a_1 <a_3 :=(\sqrt{11/3} +1)/ 4\approx 0.7287\) for \(2a^2 -a -1/3 <0\). This guarantees the asymptotic decay of the stress path to zero as described in (8.3). By this, \(E^+ >D^+\) implying \(a^3 +2a^2 -a -2/3 <0\) holds for \(a<a_2\approx 0.7131\); then,  attracts closer the direction of
attracts closer the direction of  ; otherwise,
; otherwise,  is more attractive when \(E^+ <D^+\). For \(a =1\), the condition (9) is satisfied since \(a >1/ \sqrt{3}\). For \(a>1\), the conditions (10.2) and (10.3) for stable decay can be realized only for special initial states
is more attractive when \(E^+ <D^+\). For \(a =1\), the condition (9) is satisfied since \(a >1/ \sqrt{3}\). For \(a>1\), the conditions (10.2) and (10.3) for stable decay can be realized only for special initial states  . In all other cases, the stress path grows to infinity. Since \(a_\mathrm{phys} <1\), we summarize the result in Table 3.
. In all other cases, the stress path grows to infinity. Since \(a_\mathrm{phys} <1\), we summarize the result in Table 3.
7 Conclusions
In the paper, for a constitutive model based on the concept of hypoplasticity of the Kolymbas type the stress paths obtained under proportional deformations are investigated. In particular, a simplified hypoplastic constitutive equation is considered where the objective stress rate is a function of the current stress and strain rate. The model is obtained by omitting the influence of the change in the pressure-dependent relative density in the hypoplastic model originally proposed by Bauer and Gudehus. For arbitrary proportional deformations starting from the stress-free state, the corresponding stress paths are linear which is in accordance with the first law by Goldscheider and also an important property for constitutive models relevant to frictional granular materials. From experiments, it is known that significant changes in the density of the granular material can lead to a slightly curved stress path which can also be influenced by grain crushing under higher stresses. Such properties can be taken into account using more enhanced hypoplastic models, which are not considered in the present paper.
The hypoplastic equation considered only includes two constitutive constants: a stiffness parameter and a limit stress state parameter. The former can be related to an isotropic compression test and the latter to the so-called critical friction angle defined in the steady state of a cohesionless granular material under triaxial compression. Although the influence of the direction of the stress deviator on the limit stress state parameter is neglected, it does not mean a restriction of the general results drawn. A relevant relation between the values for the direction of the stress deviator of triaxial compression and the one for another direction can, for instance, be obtained by interpolation.
For the hypoplastic constitutive equation considered, the analytical solution of the stress paths depending on monotonous linear deformation paths is obtained in a closed form. On its basis, the course of the stress paths is examined in dependence of the material parameters and prescribed proportional contractant, dilatant, and volume-preserving deformations. It is shown that stress paths starting from arbitrary initial stress states are usually nonlinear, and their convergence to a proportional stress path (second law by Goldscheider) is asymptotically stable only for a certain domain of the limit stress state parameter, which is related to the critical friction angle.
Notes
What is at first small is often extremely large in the end. And so it happens that whoever deviates only a little from truth in the beginning is led farther and farther afield in the sequel, and to errors which are a thousand times as large (F. Brentano, On the Several Senses of Being in Aristotle. Herder-Verlag, Freiburg, 1862).
References
Annin, B.D., Kovtunenko, V.A., Sadovskii, V.M.: Variational and hemivariational inequalities in mechanics of elastoplastic, granular media, and quasibrittle cracks. In: Tost, G.O., Vasilieva, O. (eds.) Analysis, Modelling, Optimization, and Numerical Techniques. Springer Proceedings in Mathematics & Statistics, vol. 121, pp. 49–56. Springer, Berlin (2015)
Armstrong, P.J., Frederick, C.O.: A mathematical representation of the multiaxial Bauschinger effect. C.E.G.B. report RD/B/N, vol. 731 (1966)
Bauer, E.: Calibration of a comprehensive hypoplastic model for granular materials. Soils Found. 36, 13–26 (1996)
Bauer, E.: Conditions for embedding Casagrande’s critical states into hypoplasticity. Mech. Cohes. Frict. Mat. 5, 125–148 (2000)
Bauer, E.: Modelling limit states within the framework of hypoplasticity. In: Goddard, J., Giovine, P., Jenkin, J.T. (eds.) AIP Conference Proceedings, vol. 1227, pp. 290–305. AIP (2010)
Bauer, E., Herle, I.: Stationary states in hypoplasticity. In: Kolymbas, D. (ed.) Constitutive Modelling of Granular Materials, pp. 167–192. Springer, Berlin (2000)
Bauer, E., Huang, W.: Influence of density and pressure on spontaneous shear band formations in granular materials. In: Ehlers, W. (ed.) Proceedings of the IUTAM Symposium on Theoretical and Numerical Methods in Continuum Mechanics of Pourous Materials, Stuttgart 1999, Germany, Kluwer, pp. 245–250 (2001)
Bauer, E., Kovtunenko, V.A., Krejčí, P., Krenn, N., Siváková, L., Zubkova, A.V.: Modified model for proportional loading and unloading of hypoplastic materials. In: Korobeinikov, A., Caubergh, M., Lazaro, T., Sardanyes, J. (eds.) Extended Abstracts Spring 2018, Series Trends in Mathematics, vol. 11, pp. 201–210. Birkhäuser, Ham (2019)
Bauer, E., Wu, W.: A hypoplastic model for granular soils under cyclic loading. In: Kolymbas, D. (ed.) Proceedings International Workshop Modern Approaches to Plasticity, pp. 247–258. Elsevier (2010)
Bauer, E., Wu, W., Huang, W.: Influence of initially transverse isotropy on shear banding in granular materials. In: Labuz, J.F., Drescher, A. (eds.) Proceedings of the International Workshop on Bifurcation and Instabilities in Geomechanics. Minneapolis, Minnesota, 2002, pp. 161–172. Balkema Press (2003)
Brokate, M., Krejčí, P.: Wellposedness of kinematic hardening models in elastoplasticity. RAIRO Modél. Math. Anal. Numér. 32, 177–209 (1998)
Chambon, R., Desrues, J., Hammad, W., Charlier, R.: CLoE, a new rate-type constitutive model for geomaterials, theoretical basis and implementation. Int. J. Numer. Anal. Methods Geomech. 18, 253–278 (1994)
Chu, J., Lo, S.-C.R.: Asymptotic behaviour of a granular soil in strain path testing. Géotechnique 44, 65–82 (1994)
Darve, F.: Une formulation Incrémentale des lois Rhéologiques, application aux Sols. Ph.D. Thesis, Université de Grenoble (1978)
Darve, F.: Incrementally non-linear constitutive relationships. In: Darve, F. (ed.) Geomaterials, Constitutive Equations and Modelling, pp. 213–238. Elsevier, Horton (1990)
Ebrahimian, B., Bauer, E.: Numerical simulation of the effect of interface friction of a bounding structure on shear deformation in a granular soil. Int. J. Numer. Anal. Methods Geomech. 36, 1486–1506 (2012)
Fellin, W., Ostermann, A.: The critical state behaviour of barodesy compared with the Matsuoka–Nakai failure criterion. Int. J. Numer. Anal. Methods Geomech. 37, 299–308 (2013)
Goldscheider, M.: True triaxial tests on dense sand. In: Workshop on Constitutive Relations for Soils, Grenoble, pp. 11–54 (1982)
Gudehus, G.: A comprehensive constitutive equation for granular materials. Soils Found. 36, 1–12 (1996)
Gudehus, G.: Physical Soil Mechanics. Springer, Berlin (2011)
Gudehus, G., Goldscheider, M., Winter, H.: Mechanical properties of sand and clay and numerical integration methods: some sources of errors and bounds of accuracy. In: Gudehus, G. (ed.) Finite Elements of Geomechanics, pp. 121–150. Wiley, New York (1997)
Gudehus, G., Mašín, D.: Graphical representation of constitutive equations. Géotechnique 59, 147–151 (2009)
Huang, W., Bauer, E.: Numerical investigations of shear localization in a micro-polar hypoplastic material. Int. J. Numer. Anal. Methods Geomech. 27, 325–352 (2003)
Huang, W., Nübel, K., Bauer, E.: Polar extension of a hypoplastic model for granular materials with shear localization. Mech. Mat. 34, 563–576 (2002)
Jerman, J., Mašín, D.: Discrete element investigation of rate effects on the asymptotic behaviour of granular materials. In: Rinaldi, V., Zeballos, M., Clari, J. (eds.) Proceedings of the 6th International Symposium on Deformation Characteristics of Geomaterials, IS-Buenos Aires 2015, 15–18 November 2015, pp. 695–702. Buenos Aires, Argentina (2015)
Jiang, Y., Liu, M.: Similarities between GSH, hypoplasticity and KCR. Acta Geotechnica 11, 519–537 (2016)
Khludnev, A.M., Kovtunenko, V.A.: Analysis of Cracks in Solids. WIT-Press, Southampton (2000)
Kolymbas, D.: Eine konstitutive Theorie für Böden und andere körnige Stoffe. Institut fur Bodenmechanik und Felsmechanik der Universität Karlsruhe, Karlsruhe (1988)
Kolymbas, D.: An outline of hypoplasticity. Arch. Appl. Mech. 61, 143–151 (1991)
Kolymbas, D.: Barodesy: a new hypoplastic approach. Int. J. Numer. Anal. Methods Geomech. 36, 1220–1240 (2012)
Kolymbas, D., Medicus, G.: Genealogy of hypoplasticity and barodesy. Int. J. Numer. Anal. Methods Geomech. 40, 2532–2550 (2016)
Kovtunenko, V.A., Krejčí, P., Bauer, E., Siváková, L., Zubkova, A.V.: On Lyapunov stability in hypoplasticity. In: Mikula, K., Ševčovič, D., Urbán, J. (eds.) Proceedings of Equadiff 2017 Conference, pp. 107–116, Slovak University of Technology, Bratislava (2017)
Kovtunenko, V.A., Zubkova, A.V.: Mathematical modelling of a discontinuous solution of the generalized Poisson–Nernst–Planck problem in a two-phase medium. Kinet. Relat. Mod. 11, 119–135 (2018)
Mašín, D.: Asymptotic behaviour of granular materials. Granular Matter 14, 759–774 (2012)
Mašín, D.: Clay hypoplasticity with explicitly defined asymptotic states. Acta Geotechnica 8, 481–496 (2013)
Mašín, D.: Modelling of Soil Behaviour with Hypoplasticity: Another Approach to Soil Constitutive Modelling. Springer, Switzerland (2019)
Mašín, D., Herle, I.: Improvement of a hypoplastic model to predict clay behaviour under undrained conditions. Acta Geotechnica 2, 261–268 (2007)
Medicus, G., Kolymbas, D., Fellin, W.: Proportional stress and strain paths in barodesy. Int. J. Numer. Anal. Methods Geomech. 40, 509–522 (2016)
Nakai, T.: Modeling of soil behavior based on \(t_{ij}\) concept. In: Proceedings of 13th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering, Kolkata, vol. 2, pp. 69–89 (2007)
Niemunis, A.: Extended Hypoplastic Models for Soils. Habilitation thesis, Ruhr University, Bochum (2002)
Niemunis, A., Herle, I.: Hypoplastic model for cohesionless soils with elastic strain range. Mech. Cohes. Frict. Mat. 2, 279–299 (1997)
Svendsen, B., Hutter, K., Laloui, L.: Constitutive models for granular materials including quasi-static frictional behaviour: toward a thermodynamic theory of plasticity. Continuum Mech. Therm. 4, 263–275 (1999)
Toll, S.: The dissipation inequality in hypoplasticity. Acta Mechanica 221, 39–47 (2011)
Topolnicki, M., Gudehus, G., Mazurkiewicz, B.K.: Observed stress–strain behaviour of remoulded saturated clays under plane strain conditions. Géotechnique 40, 155–187 (1990)
Valanis, K.C.: A theory of viscoplasticity without a yield surface. Arch. Mech. 23, 517–533 (1971)
von Wolffersdorff, P.-A.: A hypoplastic relation for granular materials with a predefined limit state surface. Mech. Cohes. Frict. Mat. 1, 251–271 (1996)
Wang, C.C.: A new representation theorem for isotropic functions, part I and II. J. Rational Mech. Anal. 36, 166–223 (1970)
Wu, W.: Hypoplastizität als mathematisches Modell zum mechanischen Verhalten granularer Stoffe. Ph.D. thesis, Institut für Bodenmechanik und Felsmechanik der Universität Karlsruhe, Karlsruhe, Germany (1992)
Wu, W., Bauer, E., Kolymbas, D.: Hypoplastic constitutive model with critical state for granular materials. Mech. Mater. 23, 45–69 (1996)
Acknowledgements
Open access funding provided by Austrian Science Fund (FWF). The authors thank two referees for the comments which helped to improve the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the OeAD Scientific and Technological Cooperation (WTZ CZ 01/2016 and 18/2020) financed by the Austrian Federal Ministry of Science, Research and Economy (BMWFW) and by the Czech Ministry of Education, Youth and Sports (MŠMT). Further support by the Austrian Science Fund (FWF) under Project No. P26147-N26 (PION) (Victor A. Kovtunenko and Anna V. Zubkova), the research Project RFBR 19-51-50004 and JSPS J19-721 (Victor A. Kovtunenko), the Grant IGDK1754 (Anna V. Zubkova), and by the European Regional Development Fund, Project No. CZ.02.1.01/0.0/0.0/16_019/0000778 (P. Krejčí) is gratefully acknowledged.
Appendix
Appendix
We start with the following consequences of formula (2.3).
Step 1: The double dot product of (2.3) with  and recalling
and recalling  leads to:
leads to:

The double dot product of (2.3) with  and using
and using  leads to:
leads to:

For  and , subsequently dividing (16.1) with
and , subsequently dividing (16.1) with  , multiplying (16.2) with
, multiplying (16.2) with  , subtracting them and using
, subtracting them and using  , this results in the linear differential equation:
, this results in the linear differential equation:

which admits the exact solution expressed in the following analytical form:

Step 2: We insert (16.4) in (2.3) such that it becomes linear in  :
:

In the sequel, it will be useful to introduce an auxiliary function such that

that is:

Then (17.1) can be rewritten equivalently as

The double dot product of (17.4) with  leads to a linear differential equation for
leads to a linear differential equation for  :
:

which admits the exact integral depending on parameter s:

Step 3: We plug (17.2), (17.4), and (17.6) in the following differential quotient:

and after its integration, we derive the solution in the closed form:

or, equivalently, as the sum of two exponential functions:

The above consideration holds true for  . Otherwise, if
. Otherwise, if  implying
implying  for \(a\not =0\), then (16.3) follows the solution:
for \(a\not =0\), then (16.3) follows the solution:

Consequently, with the function

from (16.2) we find  , and similarly to (18.1), this follows the linear equation
, and similarly to (18.1), this follows the linear equation  and its solution:
and its solution:

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bauer, E., Kovtunenko, V.A., Krejčí, P. et al. On proportional deformation paths in hypoplasticity. Acta Mech 231, 1603–1619 (2020). https://doi.org/10.1007/s00707-019-02597-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-019-02597-3



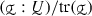 and find its solution;
and find its solution;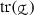 and solve it;
and solve it; in the closed form.
in the closed form.

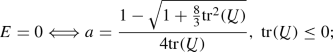

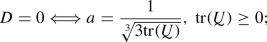
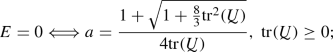
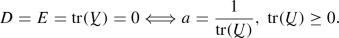
 ;
; ;
; , while in the other areas the asymptotic behaviour is independent of the initial stress state.
, while in the other areas the asymptotic behaviour is independent of the initial stress state.
 under volume-preserving deformation
under volume-preserving deformation
