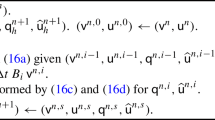1 Introduction

The Navier–Stokes equations governing the motion of viscous compressible fluids have numerous applications in engineering, physics, meteorology or biomedicine. In this paper we consider the viscous barotropic fluid endowed, for simplicity, with the isentropic pressure–density state equation \(p= a \varrho ^{\gamma },\) where \(a > 0\) is a positive constant, and \(\gamma >1\) denotes the adiabatic coefficient. The global-in-time existence of weak solutions is known for any \(\gamma > \frac{d}{2}\) in the d-dimensional setting, see Lions [20] and Feireisl [7]. More recently, Plotnikov and Vaigant [27] extended the existence theory for any \(\gamma \ge 1\) if \(d=2\). Unfortunately, the multilevel approach used in the existence proof is rather difficult to adapt directly to a numerical scheme; whence the numerical analysis of the problem remains rather incomplete.

In the last few decades, many efficient and robust numerical methods have been proposed to simulate the motion of viscous compressible fluid flows. We refer the reader to the monographs by Dolejší and Feistauer [2], Eymard et al. [5], Feistauer [3], Feistauer et al. [4], Toro [28], and the references therein. Despite a good agreement of the obtained results with experiments, a rigorous convergence analysis with the associated error estimates has been performed only in a few particular cases.

In his truly pioneering work, Karper [18], see also [9], showed convergence (up to a subsequence) of a mixed finite element-finite volume (or discontinuous Galerkin) approximation to a weak solution of the compressible multidimensional Navier–Stokes system under the technical restriction \(\gamma > 3\). His proofs basically follow step by step the existence theory developed in [7] and as such is difficult to adapt to other numerical methods. Moreover, as the weak solutions are not known to be unique, the result holds up to a subsequence and no convergence rate is available.

Recently, see [10,11,12], we have developed a new approach based on the concept of more general dissipative weak (dissipative measure-valued) solutions, which, combined with the weak–strong uniqueness and conditional regularity results, yields a rigorous proof of convergence for the mixed finite element-finite volume, finite volume and finite difference Marker-and-Cell (MAC) methods for any \(\gamma >1\) as long as the sequence of the numerical solution remains uniformly bounded and/or if the strong solution exists. The aim of the present paper is to derive error estimates for the finite volume and the MAC methods for the full range of the adiabatic coefficient \(\gamma >1.\)

There are several results concerning error estimates for the compressible Navier–Stokes equations. Under the assumption of the \(L^2\)-bounds of the discrete derivatives of the numerical solutions, Jovanović [17] studied the convergence rate of a finite volume-finite difference method to the barotropic Navier–Stokes system. In [21, 22] Liu analyzed the errors for \(P^k\) conforming finite element method, \(k\ge 2\), assuming the existence of a suitably regular smooth solution. However, the stability of the method with respect to the discrete energy was not investigated.

Furthermore, Gallouët et al. [14, 15] analyzed the unconditional convergence rates of the mixed finite volume-finite element method [9] and the MAC scheme for \(\gamma >3/2\) in the dimension \(d=3\). Similar results have been obtained by Mizerová and She [24]. All the above mentioned convergence results are based on a discrete version of the relative energy inequality estimating the error between the numerical and the strong solution. The obtained convergence error is \({\mathcal {O}}(h^A),\) where \(h>0\) is a mesh parameter and \(A = \min \left\{ \frac{2\gamma -3}{\gamma },\frac{1}{2} \right\} \), cf. [14, 15, 24]. In particular, the convergence order tends to zero when \(\gamma \rightarrow \frac{3}{2}\) and remains positive only if \(\gamma >3/2.\) Moreover, if \(\gamma \ge 2 \), the convergence rate is only \(\frac{1}{2}\) in the energy norm, though the numerical experiments indicate the second-order convergence rate.

In view of the existing results, the main novelty of the present paper is twofold:

  • Extending the error analysis to the full range \(\gamma > 1\).

  • Improving the convergence rate via a detailed consistency and error analysis.

Following the strategy proposed in the monograph [12, Chapter 9], we combine the standard consistency errors with the “continuous” form of the relative energy inequality. In contrast with the existing methods based on ad hoc construction of an approximate relative energy inequality, the new approach is rather versatile and free of additional discretization errors. In particular, we can handle any consistent energy stable numerical method in the same fashion. We focus on the finite volume method proposed in [12] and the MAC method from [24]. The application to the mixed finite element-finite volume method of Karper [18] was studied independently and presented in the recent work by Novotný and Kwon [19]. Compared to the previous results of Gallouët et al. [14, 15], we employ the consistency formulation of the numerical solution where the test function is smooth. This new approach avoids the complicated integration by parts formulae on the discrete level and improves the convergence rates of the MAC method presented in [14, 24].

The paper is organized in the following way. After presenting the continuous model and the corresponding relative energy, we formulate the numerical schemes: the finite volume and the MAC method, see Sect. 2. Next, we discuss their energy stability and consistency. The main results on the error estimates are formulated and proved in Sect. 3.

1.1 Compressible Navier–Stokes system

We begin with formulating the compressible Navier–Stokes system

$$\begin{aligned} \begin{aligned}&\partial _t \varrho + \textrm{div} _x(\varrho \varvec{u}) = 0, \\&\partial _t (\varrho \varvec{u}) + \textrm{div} _x(\varrho \varvec{u}\otimes \varvec{u}) + \nabla _xp(\varrho ) = \textrm{div} _x\mathbb {S} \end{aligned} \end{aligned}$$
(1.1)

in the time-space cylinder \([0,T] \times \Omega \), \(\Omega \subset R^d, d=2,3\), where \(\varrho \) is the density, \(\varvec{u}\) is the velocity field, and \( \mathbb {S}\) is the viscous stress tensor given by

$$\begin{aligned} \mathbb {S}= \mu \left( \nabla _x\varvec{u}+ \nabla _x^T \varvec{u}- \frac{2}{d} \textrm{div} _x\varvec{u}\mathbb {I}\right) + \lambda \textrm{div} _x\varvec{u}\mathbb {I},\; \mu >0, \quad \lambda \ge 0. \end{aligned}$$

The pressure is assumed to satisfy the isentropic law

$$\begin{aligned} p=a \varrho ^\gamma , \; a>0, \quad \gamma >1. \end{aligned}$$
(1.2)

To avoid technical problems related to a proper numerical approximation of the physical boundary, we impose the periodic boundary conditions and identify the computational domain with the flat torus

$$\begin{aligned} \Omega =\mathbb {T}^d\equiv \left( [0,1] |_{\{ 0,1 \}} \right) ^d. \end{aligned}$$

The system (1.1) is supplemented with finite energy initial data \((\varrho _0, \varvec{u}_0): \mathbb {T}^d\rightarrow \mathbb {R}^+ \times \mathbb {R}^d\),

$$\begin{aligned}{} & {} \varrho (0,x) = \varrho _0 > 0, (\varrho \varvec{u})(0,x) = \varrho _0 \varvec{u}_0,\ \text{ and } \nonumber \\ {}{} & {} E_0 = \int _{\mathbb {T}^d} \left( \frac{1}{2} \varrho _0 | \varvec{u}_0 |^2 + {P} (\varrho _0) \right) \,\textrm{d}x < \infty , \end{aligned}$$
(1.3)

where \( {P} \) is the so-called pressure potential, \( {P} (\varrho ) = \frac{a \varrho ^{\gamma }}{\gamma -1}\) for the isentropic gas law (1.2).

1.2 Relative energy

The main tool to evaluate the distance between numerical and strong solutions is the relative energy functional, cf. [8]:

$$\begin{aligned}{} & {} {\mathfrak {E}}(\varrho , \varvec{u}| r, \varvec{U}) = \int _{\mathbb {T}^d} \left( \frac{1}{2} \varrho \left|\varvec{u}- \varvec{U} \right|^2 + \mathbb {E}(\varrho |r) \right) \,\textrm{d}x, \text{ with } \\ {}{} & {} \mathbb {E}(\varrho |r)= {P} (\varrho ) - {P} '(r) (\varrho -r ) - {P} (r). \end{aligned}$$

As pointed out, relative energy functionals are often used to estimate the distance between a suitable weak solution and the strong solution; whence yielding the weak-strong uniqueness property. Recently, a discrete version of the relative energy has been applied in the error analysis of numerical schemes, see [14, 15, 24].

1.3 Classical solutions

It will be useful to identify the regularity class of smooth (classical) solutions to the Navier–Stokes system (1.1) inherited from the initial data (1.3). The following result can be deduced from [1, Theorem 3.3] and [6, Proposition 2.2].

Proposition 1.1

Let the initial data belong to the class

$$\begin{aligned} \varrho _0 \in C^3( \mathbb {T}^d), \ \varrho _0 > 0 \ \text{ in }\ \mathbb {T}^d,\ \varvec{u}_0 \in C^3( \mathbb {T}^d; R^d). \end{aligned}$$

Let \((\varrho , \varvec{u})\) be a weak solution to problem (1.1) originating from the initial data (1.3) such that

$$\begin{aligned} 0 \le \varrho \le {\bar{r}} \quad \text{ and } \quad | \varvec{u}| \le {\bar{u}} \text{ a.e. } \text{ in } (0,T) \times \mathbb {T}^d. \end{aligned}$$
(1.4)

Then \((\varrho , \varvec{u})\) is a classical solution of (1.1)–(1.3) in \([0,T] \times \mathbb {T}^d\).

If, in addition, \(\varrho _0\), \(\varvec{u}_0\) belong to the class

$$\begin{aligned} \varrho _0 \in W^{k,2}({\mathbb {T}^d}), \qquad \varvec{u}_0 \in W^{k,2}(\mathbb {T}^d; \mathbb {R}^d), \quad k \ge 6, \end{aligned}$$
(1.5)

then \(\varrho \in C([0,T]; W^{k,2}(\mathbb {T}^d))\), \(\varvec{u}\in C([0,T]; W^{k,2}(\mathbb {T}^d; \mathbb {R}^d))\), and the following estimate hold

$$\begin{aligned}{} & {} { \Vert \partial _t^\ell \varrho \Vert _{C([0,T] \times \mathbb {T}^d) } +} \Vert \varrho \Vert _{C^1([0,T] \times \mathbb {T}^d )} + \Vert 1/\varrho \Vert _{C([0,T] \times {\mathbb {T}^d})} + \Vert \varrho \Vert _{C([0,T]; W^{k,2}(\mathbb {T}^d) ) }\nonumber \\ {}{} & {} \quad \le D,\ \ell = 1,2, \nonumber \\{} & {} { \Vert \partial _t^\ell \varvec{u}\Vert _{C([0,T] \times \mathbb {T}^d;\mathbb {R}^d) } } + \Vert \varvec{u}\Vert _{C^1([0,T] \times \mathbb {T}^d;\mathbb {R}^d )} + \Vert \varvec{u}\Vert _{C([0,T]; W^{k,2}(\mathbb {T}^d; \mathbb {R}^d))}\nonumber \\ {}{} & {} \quad \le D, \ \ell = 1,2, \end{aligned}$$
(1.6)

where D depends solely on \(T, {\bar{r}}, {\bar{u}}\) and the initial data \((\varrho _0, \varvec{u}_0)\) via the norm \(\Vert (\varrho _0, \varvec{u}_0) \Vert _{W^{k,2}(\mathbb {T}^d; \mathbb {R}^{d + 1})}\) and \(\min _{x \in {\mathbb {T}^d}} \varrho _0(x).\)

Proof

The first part was proved in [6, Proposition 2.2] via the local existence theory by Valli and Zajaczkowski [26] combined the weak–strong uniqueness principle and the conditional regularity result by Sun et al. [25]. In particular, the bounds (1.6) were established for \(k = 3\), \(\ell = 1\).

Next, as shown in [1, Theorem 3.3], the solution inherits higher Sobolev regularity from the data as long as the norm \(\Vert \varvec{u}\Vert _{C([0,T]; W^{2,\infty }(\mathbb {T}^d; \mathbb {R}^d))}\) is controlled. In particular, the estimates (1.6) can be established. Similarly to Gallagher [13], the proof in [1] is based on the particular isentropic form of the pressure that enables to transform the problem to a parabolic perturbation of a symmetric hyperbolic system. \(\square \)

2 Numerical methods

First, we introduce suitable notation. By c we denote a positive constant independent of the discretization parameters \(\Delta t\) and h. We shall frequently write \(A \lesssim B\) if \(A \le cB\) and \(A\approx B\) if \(A \lesssim B\) and \(B \lesssim A\). We also write \(c\in \text {co}\{a,b\} \) if \(\min (a,b)\le c\le \max (a,b)\). Moreover, we denote by \(\Vert \cdot \Vert _{L^p}\), \(\Vert \cdot \Vert _{L^pL^q}\), and \(\Vert \cdot \Vert _{L^pW^{q,s}}\) the norms \(\Vert \cdot \Vert _{L^p(\mathbb {T}^d)},\)   \(\Vert \cdot \Vert _{L^p(0,T;L^q(\mathbb {T}^d))}\), and \(\Vert \cdot \Vert _{L^p(0,T;W^{q,s}(\mathbb {T}^d))},\) respectively.

2.1 Time discretization

We divide the time interval [0, T] into \(N_t\) equidistant parts with a fixed time increment \(\Delta t\) (\( =T/ N_t\)). For a function \(f^n\) given at the discrete time instances \(t_n = n \Delta t\), \(n=0,1,\ldots ,N_t\), we define a piecewise constant approximation f(t) in the following way

$$\begin{aligned} f(t,\cdot ) = f^0\ \text { for }\ t < \Delta t \text{ and } f(t)= f^n \ \text { for }\ t\in [n\Delta t,(n+1)\Delta t), \; n\in \{1, \ldots , N_t \}. \end{aligned}$$

The time derivative is approximated by the backward Euler method

$$\begin{aligned} D_t f = \frac{ f(t,\cdot ) - f(t-\Delta t,\cdot )}{\Delta t} \quad \text{ for } \text{ all } t \in [0,T]. \end{aligned}$$

2.2 Space discretization

To begin, we introduce a uniform structured mesh including primary, dual, and bidual grids.

Primary grid

We call \({\mathcal {T}}\) the primary grid with the following properties and notations:

  • The domain \(\mathbb {T}^d\) is divided into compact uniform quadrilaterals \( \mathbb {T}^d=\bigcup _{K\in {\mathcal {T}}} K\), where \({\mathcal {T}}\) is the set of all elements that form the primary grid.

  • \({\mathcal {E}}\) denotes the set of all faces of the primary grid \({\mathcal {T}}\). Given an element \(K\in {\mathcal {T}}\), \({\mathcal {E}}(K)\) is the set of its faces; \({\mathcal {E}}_i\) is the set of all faces that are orthogonal to the unit basis vector \(\varvec{e}_i\); \( {\mathcal {E}}_i(K)= {\mathcal {E}}(K)\cap {\mathcal {E}}_i\) for any \(i \in \{1, \ldots , d \}\).

  • h denotes the uniform size of the grid, meaning \(|x_K-x_L|= h\) for any neighbouring elements K and L, where \(x_K\) and \(x_L\) are the centers of K and L, respectively.

  • \(\sigma _{K\text {,} i -}\) and \(\sigma _{K\text {,} i +}\) denote the left and right face of an element K in the \( i{\text {th}}\)-direction, respectively.

  • \({\mathcal {N}}(K)\) denotes the set of all neighbouring elements of \(K \in {\mathcal {T}}.\)

  • \(\sigma = K|L\) denotes the face \(\sigma \) that separates the elements K and L. Moreover, \(\sigma = \overrightarrow{K|L}\) means \(\sigma = K|L\) and \(x_L - x_K = h\varvec{e}_i\) for some \(i \in \{1, \ldots , d \}\).

  • \(\varvec{n}\) denotes the outer normal of a generic face \(\sigma \) and \(\varvec{n}_{\sigma , K}\) denotes the outer normal vector to a face \(\sigma \in {\mathcal {E}}(K).\)

Dual grid

The dual of the primary grid is determined as follows.

  • For any face \(\sigma =K|L\in {\mathcal {E}}_i\), a dual cell is defined as \(D_\sigma =D_{\sigma ,K} \cup D_{\sigma ,L}\), where \(D_{\sigma ,K} = \{x\in K, x_i \in \text {co}\{(x_K)_i, (x_\sigma )_i \} \}\), see Fig. 1a for a two dimensional graphic illustration.

  • \({\mathcal {D}}_i=\left\{ D_\sigma \; | \; \sigma \in {\mathcal {E}}_i\right\} \), \(i \in \{1, \ldots , d \}\), represents the \( i{\text {th}}\) dual grid of \({\mathcal {T}}\). Note that for each fixed \(i \in \{1, \ldots , d \}\) it holds

    $$\begin{aligned} \mathbb {T}^d=\bigcup _{\sigma \in {{\mathcal {E}}_i}} D_{\sigma }, \;\; \textrm{int}(D_\sigma )\cap \textrm{int}( D_{\sigma '})=\emptyset \text{ for } \sigma ,\sigma '\in {{\mathcal {E}}_i},\,\sigma \ne \sigma '. \end{aligned}$$

  • \({\widetilde{{\mathcal {E}}}}_i\) is the set of all faces of the \( i{\text {th}}\) dual grid \({\mathcal {D}}_i\) and \( {\widetilde{{\mathcal {E}}}}_{i,j}= \{ \epsilon \in {\widetilde{{\mathcal {E}}}}_i | \epsilon \text{ is } \text{ orthogonal } \text{ to } \varvec{e}_j\}\).

  • A generic face of a dual cell \(D_\sigma \) is denoted as \(\epsilon \in {\widetilde{{\mathcal {E}}}}(D_\sigma )\), where \({\widetilde{{\mathcal {E}}}}(D_\sigma )\) denotes the set of all faces of \(D_\sigma .\)

  • \(\epsilon = D_\sigma | D_{\sigma '}\) denotes a dual face that separates the dual cells \(D_\sigma \) and \(D_{\sigma '}\). Moreover, \(\epsilon = \overrightarrow{ D_\sigma | D_{\sigma '} }\) means \(\epsilon = D_\sigma | D_{\sigma '}\) and \(x_{\sigma '} - x_{\sigma } = h \varvec{e}_i\) for some \(i \in \{ 1,\ldots , d\}\).

  • \( {\mathcal {N}}^\star (\sigma )\) denotes the set of all faces whose associated dual elements are the neighbours of \(D_\sigma ,\) i.e.,

    $$\begin{aligned} {\mathcal {N}}^\star (\sigma )=\{\sigma '\ |\ D_{\sigma '} \text{ is } \text{ a } \text{ neighbour } \text{ of } D_\sigma \}. \end{aligned}$$

Bidual grid

  • Similarly to the definition of the dual cell, a bidual cell \(D_\epsilon := D_{\epsilon ,\sigma } \cap D_{\epsilon ,\sigma '}\) associated to \(\epsilon = D_\sigma | D_{\sigma '} \in {\widetilde{{\mathcal {E}}}}_{i,j}\) is defined as the union of adjacent halves of \(D_\sigma \) and \(D_{\sigma '}\), where \(D_{\epsilon ,\sigma } = \{x \in D_{\sigma }| x_j \in \text {co}\{(x_\sigma )_j, (x_\epsilon )_j \} \} \) see Fig. 1b for a two dimensional graphic illustration.

  • \({\mathcal {B}}_{i,j}\) denotes the \(j^{\textrm{th}}\) dual grid of \({\mathcal {D}}_i\), which is a set of all bidual cells associated with the bidual faces of \( {\widetilde{{\mathcal {E}}}}_{i,j}\). Note that \({\mathcal {B}}_{i,j}= {\mathcal {T}}\) in the case of \(i=j\).

Fig. 1
figure 1

MAC grid in two dimensions

Full size image

Discrete function spaces. We introduce the following spaces of piecewise constant functions:

$$\begin{aligned} \begin{aligned} Q_h&= \left\{ \phi \mid \phi _h|_K = \text { constant } \text{ for } \text{ all } \; K\in {\mathcal {T}}\right\} , \qquad \textbf{Q}_h=Q_h^{d}, \\ \textbf{W}_h&=\left( W_{1,h},\ldots W_{d,h} \right) , \quad \\ W_{i,h}&= \left\{ \phi \mid \phi _h|_{D_\sigma } = \text { constant } \text{ for } \text{ all } \; \sigma \in {\mathcal {E}}_i\right\} , \; i\in \{1, \ldots , d \}. \end{aligned} \end{aligned}$$

The corresponding projections read

$$\begin{aligned} \Pi _Q:&L^1(\mathbb {T}^d) \rightarrow Q_h, \quad \Pi _Q\phi = \sum _{K\in {\mathcal {T}}} (\Pi _Q\phi )_K 1_{K}, \quad (\Pi _Q\phi )_K = \frac{1}{|K|} \int _{K} \phi \,\textrm{d}x, \\ \Pi _ {\mathcal {E}}^{(i)}:&W^{1,1}(\mathbb {T}^d) \rightarrow W_{i,h}, \quad \Pi _ {\mathcal {E}}^{(i)}\phi = \sum _{\sigma \in {\mathcal {E}}} ( \Pi _ {\mathcal {E}}^{(i)}\phi )_{\sigma } 1_{D_\sigma }, \quad ( \Pi _ {\mathcal {E}}^{(i)}\phi )_{\sigma } = \frac{ 1}{|\sigma |} \int _{\sigma } \phi \,\textrm{dS}(x), \end{aligned}$$

where \(1_K\) and \(1_{D_\sigma }\) are the characteristic functions. Further, for any \(\varvec{\phi }=(\phi _1, \ldots , \phi _d)\) we denote \( \Pi _ {\mathcal {E}}\varvec{\phi }= \left( \Pi _ {\mathcal {E}}^{(1)}\phi _1, \ldots , \Pi _ {\mathcal {E}}^{(d)}\phi _d\right) .\) Moreover, for any bidual grid \(D_\epsilon \) we define

$$\begin{aligned} \Pi _{\epsilon }\phi |_{D_\epsilon } = \frac{1}{|\epsilon |} \int _{\epsilon } \phi \,\textrm{dS}(x). \end{aligned}$$
(2.1)

2.3 Discrete operators

Average and jump. First, for a piecewise smooth function \(f_h\), we define its trace

Then for any \(r_h \in Q_h\) we define the average operator

If in addition, \(\sigma \in {\mathcal {E}}_i\) for an \(i\in \{1, \ldots , d\}\), we write as and denote

Analogously to the average operator, we define the jump operator for \(r_h \in Q_h\) as

Further, for vector-valued functions and we define

Note that for any we have .

Gradient operator. For any \(r_h \in Q_h\) and we introduce the following gradient operators.

where

Furthermore, for any and \(\phi \in W^{1,2}(\mathbb {T}^d)\) we set

$$\begin{aligned}{} & {} \nabla _Q\varvec{v}_h= \sum _{K \in {\mathcal {T}}}1_K \nabla _Q\varvec{v}_h|_K \ \ \text{ with } \ \ \nabla _Q\varvec{v}_h|_K = \sum _{\sigma \in {\mathcal {E}}(K)}\frac{|\sigma |}{|K|} \left\{ \!\!\left\{ \varvec{v}_h\right\} \!\!\right\} \otimes \varvec{n}, \\{} & {} \nabla ^{ \Pi _ {\mathcal {E}}}_{\!\! {\mathcal {T}}}\phi = \left( \partial _{\mathcal {T}}^{(1)} \Pi _ {\mathcal {E}}^{(1)} \phi , \cdots , \partial _{\mathcal {T}}^{(d)} \Pi _ {\mathcal {E}}^{(d)}\phi \right) . \end{aligned}$$

Here, \( \partial _{\mathcal {T}}^{(i)} \) is defined for any \( u_{i,h} \in W_{i,h}\), \(i \in \{1, \ldots , d \}\) as

$$\begin{aligned} \begin{aligned} \partial _{\mathcal {T}}^{(i)} u_{i,h} (x) = \sum _{K \in {\mathcal {T}}}1_K ( \partial _{\mathcal {T}}^{(i)} u_{i,h} )_{K}, \quad \left. \partial _{\mathcal {T}}^{(i)} u_{i,h} \right| _{K} = \frac{ u_{i,h} |_{\sigma _{K\text {,} i +}} - u_{i,h} |_{\sigma _{K\text {,} i -}}}{h}, \ K\in {\mathcal {T}}. \end{aligned} \end{aligned}$$

Note that for any \(r_h \in Q_h\) and \( u_{i,h} \in W_{i,h}\), there hold

$$\begin{aligned} \overline{ \eth _{{{{\mathcal {D}}}}_i} r_h} = \partial _{\mathcal {T}}^{(i)} \left\{ \!\!\left\{ r_h\right\} \!\!\right\} ^{(i)} \quad \text{ and } \quad \eth _{{\mathcal {B}}_{i,i}} u_{i,h} = \partial _{\mathcal {T}}^{(i)} u_{i,h} . \end{aligned}$$

Divergence operator. For \(\varvec{u}_h\in \textbf{W}_h\) and \(\varvec{v}_h\in \textbf{Q}_h\) we define the following discrete divergence operators adjoint to the above discrete gradient operators

$$\begin{aligned}{} & {} \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h(x) = \sum _{i=1}^d \partial _{\mathcal {T}}^{(i)} u_{i,h} (x) \quad \text{ and }\quad \\{} & {} \textrm{div} _{\mathcal {T}}^{Q}\varvec{v}_h(x) = \sum _{i=1}^d \partial _{\mathcal {T}}^{(i)} \left\{ \!\!\left\{ v_{i,h} \right\} \!\!\right\} ^{(i)} (x) = \sum _{i=1}^d\overline{ \eth _{{{{\mathcal {D}}}}_i} v_{i,h} } (x). \end{aligned}$$

It is easy to observe for any that

$$\begin{aligned} \textrm{div} _{\mathcal {T}}^\textbf{W}\left\{ \!\!\left\{ \varvec{v}_h\right\} \!\!\right\} = \textrm{div} _{\mathcal {T}}^{Q}\varvec{v}_h. \end{aligned}$$
(2.2)

Upwind flux. Given a velocity field , the upwind flux function for \(r_h \in Q_h\) is given by

$$\begin{aligned} \textrm{Up}[r_h,\varvec{u}_h]_\sigma = r_h^{\textrm{in}} (u_{\sigma })^+ + r_h^{\textrm{out}} (u_{\sigma })^-, \end{aligned}$$

where

$$\begin{aligned} r^{\pm } = \frac{1}{2} (r \pm |r|), \quad u_\sigma = {\left\{ \begin{array}{ll} \left\{ \!\!\left\{ \varvec{u}_h\right\} \!\!\right\} \cdot \varvec{n}, &{} \text{ if } \varvec{u}_h\in \textbf{Q}_h, \\ \varvec{u}_h\cdot \varvec{n}, &{} \text{ if } \varvec{u}_h\in \textbf{W}_h. \end{array}\right. } \end{aligned}$$

To approximate nonlinear convective terms we apply the following diffusive upwind flux

For we define a vector-valued upwind flux componentwise

2.4 Preliminary estimates and inequalities

In this section we present preliminary material. First, it is easy to check that the following integration by parts formulae hold, see e.g. [16, Lemma 2.1].

Lemma 2.1

Let \(r_h, \phi _h \in Q_h,\) and \(\varvec{u}_h, \varvec{\phi }_h \in \textbf{W}_h.\) Then

$$\begin{aligned} \int _{\mathbb {T}^d} r_h \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h \,\textrm{d}x = - \int _{\mathbb {T}^d} \varvec{u}_h\cdot \nabla _{{{\mathcal {D}}}}r_h \,\textrm{d}x, \quad \int _{\mathbb {T}^d} r_h \partial _{\mathcal {T}}^{(i)} u_{i,h} \,\textrm{d}x = - \int _{\mathbb {T}^d} u_{i,h} \eth _{{{{\mathcal {D}}}}_i} r_h \,\textrm{d}x.\nonumber \\ \end{aligned}$$
(2.3a)

Next, we report the following useful lemmas whose proofs are presented in Appendix A.

Lemma 2.2

For any \(r_h \in Q_h\), \(\varvec{v}_h\in \textbf{Q}_h\), \(\varvec{u}_h\in \textbf{W}_h\), \(\psi \in W^{1,2}(\mathbb {T}^d)\) and \(\varvec{U}\in W^{1,2}(\mathbb {T}^d;\mathbb {R}^d)\), there hold

$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} r_h \textrm{div} _x\varvec{U} \,\textrm{d}x =\int _{\mathbb {T}^d} r_h \textrm{div} _{\mathcal {T}}^\textbf{W} \Pi _ {\mathcal {E}}\varvec{U} \,\textrm{d}x, \end{aligned}$$
(2.4)
$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \varvec{v}_h\cdot \nabla _x\psi \,\textrm{d}x = \int _{\mathbb {T}^d} \varvec{v}_h\cdot \nabla ^{ \Pi _ {\mathcal {E}}}_{\!\! {\mathcal {T}}}\psi \,\textrm{d}x. \end{aligned}$$
(2.5)

Lemma 2.3

For any \(\varvec{u}_h\in \textbf{W}_h\), \(\varvec{v}_h\in \textbf{Q}_h\) and \(\psi \in W^{1,2}(\mathbb {T}^d)\) there hold

$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \varvec{u}_h\cdot \nabla _x\psi \,\textrm{d}x = - \int _{\mathbb {T}^d} \Pi _{\epsilon }\psi \; \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h \,\textrm{d}x, \end{aligned}$$
(2.6)
$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \varvec{v}_h\cdot \nabla _x\psi \,\textrm{d}x = - \sum _{i=1}^d\int _{\mathbb {T}^d} \Pi _ {\mathcal {E}}^{(i)}\psi \; \eth _{{{{\mathcal {D}}}}_i} v_{i,h} \,\textrm{d}x. \end{aligned}$$
(2.7)

Lemma 2.4

For any \(\varvec{u}_h\in \textbf{W}_h\), \(\varvec{v}_h\in \textbf{Q}_h\) and \(\varvec{U}\in W^{2,2}(\mathbb {T}^d; \mathbb {R}^d)\), we have

$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \Pi _Q\varvec{u}_h\cdot \Delta _x \varvec{U} \,\textrm{d}x\nonumber \\ {}{} & {} \quad = - \sum _{i=1}^d\sum _{j=1}^d\sum _{\epsilon = D_\sigma |D_{\sigma '} \in {\widetilde{{\mathcal {E}}}}_{j,i}}\int _{D_\epsilon } \eth _{{\mathcal {B}}_{j,i}} u_{j,h} \left( \frac{ ( \Pi _ {\mathcal {E}}^{(i)} \partial _i U_j)_{D_\sigma } +( \Pi _ {\mathcal {E}}^{(i)} \partial _i U_j)_{D_{\sigma '}} }{2} \right) \,\textrm{d}x,\nonumber \\ \end{aligned}$$
(2.8a)
$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{U} \,\textrm{d}x = - \int _{\mathbb {T}^d} \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h \Pi _{\epsilon }( \textrm{div} _x\varvec{U}) \,\textrm{d}x, \end{aligned}$$
(2.8b)
$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \varvec{v}_h\cdot \Delta _x \varvec{U} \,\textrm{d}x = - \int _{\mathbb {T}^d} \nabla _{{{\mathcal {D}}}}\varvec{v}_h: \Pi _ {\mathcal {E}} \nabla _x\varvec{U} \,\textrm{d}x, \end{aligned}$$
(2.8c)
$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \left\{ \!\!\left\{ \varvec{v}_h\right\} \!\!\right\} \cdot \nabla _x \textrm{div} _x\varvec{U} \,\textrm{d}x =- \int _{\mathbb {T}^d} \Pi _{\epsilon } \textrm{div} _x\varvec{U}\; \textrm{div} _{\mathcal {T}}^{Q}\varvec{v}_h \,\textrm{d}x. \end{aligned}$$
(2.8d)

Lemma 2.5

Let \(\varvec{v}_h\in \textbf{Q}_h\), \(\varvec{u}_h\in \textbf{W}_h\), \(\varvec{U}\in W^{2,2}(\mathbb {T}^d; \mathbb {R}^d)\), and \(\mathbf {\Phi }\in W^{3,2}(\mathbb {T}^d; \mathbb {R}^d)\). Then for any \(i,j\in \{1, \ldots , d \}\), we have

$$\begin{aligned}{} & {} \Vert \Pi _Q\varvec{u}_h-\varvec{u}_h\Vert _{L^2} \le \frac{h}{2} \Vert \nabla _{{{\mathcal {B}}}}\varvec{u}_h\Vert _{L^2}, \quad \Vert \left\{ \!\!\left\{ \varvec{v}_h\right\} \!\!\right\} -\varvec{v}_h\Vert _{L^2} \le \frac{h}{2} \Vert \nabla _{{{\mathcal {D}}}}\varvec{v}_h\Vert _{L^2}, \end{aligned}$$
(2.9a)
$$\begin{aligned}{} & {} \Vert \Pi _ {\mathcal {E}}^{(i)} \partial _i U_j - \partial _i U_j \Vert _{L^2} \le h \Vert \varvec{U}\Vert _{W^{2,2}}, \quad \Vert \Pi _ {\mathcal {E}} \nabla _x\varvec{U}- \nabla _x\varvec{U}\Vert _{L^2} \le h\Vert \varvec{U}\Vert _{W^{2,2}}, \end{aligned}$$
(2.9b)
$$\begin{aligned}{} & {} \Vert \textrm{div} _x\varvec{U}- \Pi _{\epsilon } \textrm{div} _x\varvec{U}\Vert _{L^2} \le h\Vert \varvec{U}\Vert _{W^{2,2}}, \quad \Vert \Pi _{\epsilon } \textrm{div} _x\varvec{U}- \Pi _ {\mathcal {E}}^{(i)} \textrm{div} _x\varvec{U}\Vert _{L^2} \le h \Vert \varvec{U}\Vert _{W^{2,2}}.\nonumber \\ \end{aligned}$$
(2.9c)
$$\begin{aligned}{} & {} \Vert \partial _i U_j - \eth _{{{{\mathcal {D}}}}_i} \Pi _QU_j \Vert _{L^2} \le h \Vert \varvec{U}\Vert _{W^{2,\infty }}, \quad \Vert \nabla _x\varvec{U}- \nabla _{{{\mathcal {D}}}}\Pi _Q\varvec{U}\Vert _{L^2} \le h\Vert \varvec{U}\Vert _{W^{2,2}} \end{aligned}$$
(2.9d)

2.5 Finite volume and finite difference methods

We proceed by presenting a finite volume and a finite difference numerical method that will be used to approximate the Navier–Stokes system (1.1)–(1.3). Both methods have been already successfully applied in numerical simulations, see, e.g., [12]. In our recent work [11, 12, 24], the convergence was shown for \(\gamma > 1\) via the concept of dissipative measure-valued solutions. However, the error analysis was missing for the finite volume method and suboptimal for the finite difference method.

2.5.1 Finite volume method

We introduce the finite volume (FV) method approximating the Navier–Stokes system (1.1)–(1.3).

Definition 2.6

(FV scheme) Given the initial data (1.3), we set \((\varrho _h^0,\varrho _h^0 \varvec{u}_h^0) =(\Pi _Q\varrho _0, \Pi _Q[\varrho _0 \varvec{u}_0])\). The FV approximation \((\varrho _h^n, \varvec{u}_h^n) \in Q_h\times \textbf{Q}_h,\) \(n=1,\dots , N,\) of the Navier–Stokes system (1.1)–(1.3) is a solution of the following system of algebraic equations:

(2.10a)
(2.10b)

where \(\nu = \frac{d-2}{d} \mu + \lambda .\)

2.5.2 Finite difference MAC method

We proceed by presenting the finite difference MAC scheme that is based on a staggered grid approach. On the one hand, the discrete density \(\varrho _h\) and pressure \(p_h=p(\varrho _h)\) are approximated on the primary grid \({\mathcal {T}}\). On the other hand, the \( i{\text {th}}\) component of the velocity field \( u_{i,h} \) is approximated on the \( i{\text {th}}\) dual grid \({\mathcal {D}}_i\). The MAC scheme reads as follows.

Definition 2.7

(MAC scheme) Given the initial data (1.3), we consider \((\varrho _h^0,\varrho _h^0 \Pi _Q\varvec{u}_h^0) =(\Pi _Q\varrho _0, \Pi _Q[\varrho _0 \varvec{u}_0]).\) The MAC approximation of the Navier–Stokes system (1.1)–(1.3) is a sequence \( (\varrho _h^n,\varvec{u}_h^n ) \in Q_h\times \textbf{W}_h\), \(n=1,2,\dots ,N\), which solves the following system of algebraic equations:

(2.11a)
(2.11b)

where \(\nu = \frac{d-2}{d} \mu + \lambda .\)

In what follows, we will denote by \(\varrho _h(t), \varvec{u}_h(t)\) the piecewise constant approximations of \(\varrho _h^n, \varvec{u}_h^n\), \(n=0,1, \dots , N\) on the time interval [0, T], see Sect. 2.1. We note that both methods, the FV method (2.10) as well as the MAC method (2.11), preserve the positivity of density and conserve the mass

$$\begin{aligned} \varrho _h(t)>0\ \text{ and } \int _{\mathbb {T}^d} \varrho _h(t) \,\textrm{d}x = M \quad \text{ for } \text{ all } \; t\in (0,T), \end{aligned}$$
(2.12)

where \( M:= \int _{\mathbb {T}^d} \varrho _0 \,\textrm{d}x \) denotes the fluid mass, see e.g. [12, Lemma 11.2].

2.6 Energy stability

The essential feature of any numerical scheme is its stability. We now recall the energy stability of both numerical methods introduced above, see [12, Theorem 11.1 and 14.1]

Lemma 2.8

(Energy estimates) Let \((\varrho _h, \varvec{u}_h)\) be a numerical solution obtained either by the FV scheme (2.10) or by the MAC scheme (2.11) with \(\gamma >1\). Then for all \(\tau \in (0,T)\), it holds

$$\begin{aligned}{} & {} \int _{\mathbb {T}^d} \left( \frac{1}{2} \varrho _h\left|\Pi _Q\varvec{u}_h \right|^2 + {P} (\varrho _h) \right) (\tau ) \,\textrm{d}x + \mu \int _0^\tau \int _{\mathbb {T}^d} {\left| \nabla _h\varvec{u}_h \right|^2 } \,\textrm{d}x \textrm{dt}\nonumber \\ {}{} & {} \quad + \nu \int _0^\tau \int _{\mathbb {T}^d} \left|\textrm{div}_h\varvec{u}_h \right|^2 \,\textrm{d}x \textrm{dt}\le E_0, \end{aligned}$$
(2.13)

where \( E_0=\int _{\mathbb {T}^d} \Big (\frac{1}{2} \varrho _0 |\varvec{u}_0|^2 + {P} (\varrho _0) \Big ) \,\textrm{d}x\) is the initial energy and

$$\begin{aligned} ( \nabla _h\varvec{u}_h, \textrm{div}_h\varvec{u}_h) = {\left\{ \begin{array}{ll} ( \nabla _{{{\mathcal {D}}}}\varvec{u}_h, \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h) &{} \text{ for } \varvec{u}_h\in \textbf{Q}_h \text{ in } \text{ the } \text{ FV } \text{ scheme }; \\ ( \nabla _{{{\mathcal {B}}}}\varvec{u}_h, \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h) &{} \text{ for } \varvec{u}_h\in \textbf{W}_h \text{ in } \text{ the } \text{ MAC } \text{ scheme }. \end{array}\right. } \end{aligned}$$

Moreover, there exists \(c>0\) which may depend on the fluid mass M and the initial energy \(E_0\) but is independent of the parameters h and \(\Delta t\) such that

$$\begin{aligned}&\Vert \varrho _h\left|\Pi _Q\varvec{u}_h \right|^2\Vert _{L^{\infty }L^1} \le c , \quad \Vert \varrho _h\Vert _{L^{\infty }L^\gamma } \le c , \quad \Vert \varrho _h\Pi _Q\varvec{u}_h\Vert _{L^\infty L^{\frac{2\gamma }{\gamma +1}}} \le c , \end{aligned}$$
(2.14a)
$$\begin{aligned}&\Vert \textrm{div}_h\varvec{u}_h\Vert _{L^2L^2} \le c , \quad \Vert \nabla _h\varvec{u}_h\Vert _{L^2 L^2} \le c ,\quad \Vert \varvec{u}_h\Vert _{L^{2}L^6} \le c . \end{aligned}$$
(2.14b)

2.7 Consistency formulation

The next important ingredient of our approach is the consistency formulation of the numerical scheme.

Lemma 2.9

(Consistency formulation) Let \((\varrho _h, \varvec{u}_h)\) be either a solution of the FV scheme (2.10) or the MAC scheme (2.11) with \(\Delta t \approx h \in (0,1)\), \(\gamma >1\) and \(\varepsilon >-1\).

Then for all \(\tau \in (0,T)\), \(\phi \in L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d)),\) \( \partial _t ^2 \phi \in L^\infty ((0,T) \times \mathbb {T}^d)\) and \(\varvec{\phi }\in L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d; \mathbb {R}^d))\), \( \partial _t ^2 \varvec{\phi }\in L^\infty ((0,T) \times \mathbb {T}^d; \mathbb {R}^d)\) there hold

$$\begin{aligned}{} & {} \left[ \int _{\mathbb {T}^d} \varrho _h\phi \,\textrm{d}x \right] _{t=0}^\tau \nonumber \\ {}{} & {} \quad = \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h\partial _t \phi + \varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x\phi \right) \,\textrm{d}x \textrm{dt}\; + e_\varrho (\tau , \Delta t, h, \phi ), \end{aligned}$$
(2.15a)
$$\begin{aligned}{} & {} \left[ \int _{\mathbb {T}^d} \varrho _h\Pi _Q\varvec{u}_h\cdot \varvec{\phi } \,\textrm{d}x \right] _{t=0}^\tau \nonumber \\ {}{} & {} \quad = \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h\Pi _Q\varvec{u}_h\cdot \partial _t \varvec{\phi }+ \varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h: \nabla _x\varvec{\phi }+ p_h \textrm{div} _x\varvec{\phi } \right) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \qquad - \mu \int _0^\tau \int _{\mathbb {T}^d} \nabla _h\varvec{u}_h: \nabla _x\varvec{\phi } \,\textrm{d}x \textrm{dt}- \nu \int _0^\tau \int _{\mathbb {T}^d} \textrm{div}_h\varvec{u}_h\; \textrm{div} _x\varvec{\phi } \,\textrm{d}x \textrm{dt}\;\nonumber \\{} & {} \qquad +e_{\varvec{m}}(\tau , \Delta t, h, \varvec{\phi }), \end{aligned}$$
(2.15b)

where the consistency errors are bounded as follows:

$$\begin{aligned} \begin{aligned}&\left|e_\varrho (\tau , \Delta t, h, \phi ) \right| \le {\left\{ \begin{array}{ll} C_\varrho \big (\Delta t+ h + h^{1+\varepsilon } + h^{1+\beta _D} \big ) &{} \text{ for } \text{ the } \text{ FV } \text{ method }, \\ C_\varrho \big (\Delta t+ h^{1+\varepsilon } + h^{1+\beta _D} \big ) &{} \text{ for } \text{ the } \text{ MAC } \text{ method }, \end{array}\right. } \\&\left|e_{\varvec{m}}(\tau , \Delta t, h, \varvec{\phi }) \right| \\ {}&\qquad \le {\left\{ \begin{array}{ll} C_{\varvec{m}} \big ( \sqrt{\Delta t} + h + h^{1+\varepsilon } + h^{1+\beta _M} \big )&{} \text{ for } \text{ the } \text{ FV } \text{ method }, \\ C_{\varvec{m}} \big ( \sqrt{\Delta t} +h + h^{1+\varepsilon } + h^{1+\beta _M} + h^{1+\varepsilon + \beta _D } \big ) &{} \text{ for } \text{ the } \text{ MAC } \text{ method. } \end{array}\right. } \\ \end{aligned} \end{aligned}$$
(2.15c)

Here, the constant \(C_\varrho \) depends on

$$\begin{aligned} \text{ the } \text{ initial } \text{ energy } E_0, T, \text{ and } \Vert \phi \Vert _{ L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d)) },\, \Vert \partial _t^2 \phi \Vert _{L^\infty ((0,T) \times \mathbb {T}^d) }, \end{aligned}$$

and \(C_{\varvec{m}}\) depends on

$$\begin{aligned} E_0, T, \Vert \varvec{\phi }\Vert _{ L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d; \mathbb {R}^d) },\, \Vert \partial _t^2 \varvec{\phi }\Vert _{L^\infty ((0,T) \times \mathbb {T}^d; \mathbb {R}^d) }. \end{aligned}$$

Further, the exponents \(\beta _D\) and \(\beta _M\) are given by

$$\begin{aligned} \begin{aligned}&\left. \begin{array}{l} \beta _D = {\left\{ \begin{array}{ll} \max \left\{ - \frac{3\varepsilon +3+d}{6\gamma }, \frac{\gamma -2}{2\gamma }d \right\} , &{} \text{ if } \gamma \in (1,2), \\ 0, &{}\text{ if } \gamma \ge 2, \end{array}\right. } \end{array} \right. \quad \\ {}&\beta _M = {\left\{ \begin{array}{ll} - \frac{3\varepsilon +3+d}{6\gamma }, &{} \text{ if } \gamma \in (1,2), \\ \frac{\gamma -3}{3\gamma }d, &{} \text{ if } \gamma \in [2,3), \\ 0, &{} \text{ if } \gamma \ge 3 \text{ for } d=3,\\ 0, &{} \text{ if } \gamma > 2 \text{ for } d=2. \end{array}\right. } \end{aligned} \end{aligned}$$
(2.15d)

Remark 1

Consistency formulation for the FV and MAC method was introduced in [12, Theorem 11.2] and [12, Theorem 14.2], respectively. Instead of an abstract consistency error identified in [12], Lemma 2.9 provides an explicit bound in terms of the numerical step and regularity of the associated test function. Moreover, we improve the result of [12] by requiring less regularity of the test functions.

Remark 2

Following the recent result of Lukáčová-Medvid’ová et al. [23, Lemma B.2], we could improve the estimates on \(\beta _D\) and \(\beta _M\).

Proof of Lemma 2.9

The consistency errors arising from the time derivative term can be evaluated in the following way. First, by a direct calculation, we obtain

$$\begin{aligned}{} & {} \int _0^{t^{n+1}} \int _{\mathbb {T}^d} D_t r_h(t) \Pi _Q\varphi (t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \quad = \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \frac{r_h(t)- r_h(t-\Delta t) }{\Delta t} \varphi (t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \quad = \frac{1}{\Delta t}\int _0^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) \varphi (t) \,\textrm{d}x \textrm{dt}- \frac{1}{\Delta t}\int _{-\Delta t}^{t^n} \int _{\mathbb {T}^d} r_h(t) \varphi (t+ \Delta t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \quad = - \int _0^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) D_t \varphi (t+\Delta t) \,\textrm{d}x \textrm{dt}+ \frac{1}{\Delta t}\int _{ t^n }^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) \varphi (t +\Delta t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \qquad - \frac{1}{\Delta t}\int _{-\Delta t}^{0} \int _{\mathbb {T}^d} r_h(t) \varphi (t+ \Delta t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \quad = - \int _0^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) D_t \varphi (t+\Delta t) \,\textrm{d}x \textrm{dt}+ \frac{1}{\Delta t}\int _{t^n}^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) \varphi (t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \qquad - \frac{1}{\Delta t} \int _0^{\Delta t} \int _{\mathbb {T}^d} r_h^0 \varphi (t) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \quad = - \int _0^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) \partial _t \varphi (t) \,\textrm{d}x \textrm{dt}+ \int _{\mathbb {T}^d} \underbrace{r_h(\tau )}_{= r_h^n \, \forall \tau \in [t^n,t^{n+1}) } \varphi (\tau ) \,\textrm{d}x\nonumber \\{} & {} \quad - \int _{\mathbb {T}^d} r_h^0 \varphi (0) \,\textrm{d}x + I_1 + I_2 +I_3, \end{aligned}$$
(2.16)

for any \(\tau \in [t_n, t_{n+1})\), \(n=1,\dots , N_T\), where

$$\begin{aligned} I_1&= \int _{\mathbb {T}^d} r_h^0 \frac{1}{\Delta t} \int _0^{\Delta t} \left( \varphi (0) - \varphi (t)\right) \textrm{dt} \,\textrm{d}x \lesssim \Delta t\Vert \partial _t\varphi \Vert _{L^\infty L^\infty } \Vert r_h^0\Vert _{L^1}, \\ I_2&= \int _{\mathbb {T}^d} \frac{1}{\Delta t} \int _{t^n}^{t^{n+1}} \big ( r_h(t) \varphi (t+\Delta t) - r_h(\tau )\varphi (\tau )\big ) \textrm{dt} \,\textrm{d}x \\ {}&= \int _{\mathbb {T}^d} \frac{1}{\Delta t} \int _{t^n}^{t^{n+1}} r_h^n \big ( \varphi (t+\Delta t) - \varphi (\tau ) \big ) \textrm{dt} \,\textrm{d}x \lesssim \Delta t\Vert r_h^n\Vert _{L^1} \Vert \partial _t\varphi \Vert _{L^\infty L^\infty }, \\ I_3&= \int _0^{t^{n+1}} \int _{\mathbb {T}^d} r_h(t) \left( \partial _t \varphi (t) - D_t\varphi (t+\Delta t) \right) \,\textrm{d}x \textrm{dt}\\ {}&= \int _{\mathbb {T}^d} \sum _{k=0}^{n} \int _{t^k}^{t^{k+1}} r_h(t) \big ( \partial _t \varphi (t) - D_t\varphi (t+\Delta t) \big ) \textrm{dt} \,\textrm{d}x \\ {}&\le \Delta t\Vert \partial _{t}^2\varphi \Vert _{L^\infty L^\infty } \Vert r_h\Vert _{L^\infty L^1}. \end{aligned}$$

Collecting the above estimates we obtain from (2.16) that

$$\begin{aligned} \begin{aligned}&\left[ \int _{\mathbb {T}^d} r_h \varphi \,\textrm{d}x\right] _0^{\tau } - \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \left( D_t r_h(t) \Pi _Q\varphi (t) + r_h(t) \partial _t \varphi (t) \right) \,\textrm{d}x \textrm{dt}\\ {}&\lesssim \Delta t(\Vert \partial _{t}\varphi \Vert _{L^\infty L^\infty } +\Vert \partial _{t}^2\varphi \Vert _{L^\infty L^\infty } ) \Vert r_h\Vert _{L^\infty L^1}, \end{aligned} \end{aligned}$$
(2.17)

whenever \(\tau \in [t_n, t_{n+1})\), where (\(r_h, \varphi \)) stands for \((\varrho _h,\phi )\) or \((\varrho _h\varvec{u}_h, \varvec{\phi })\).

Analogously as in the proofs of [12, Theorem 11.2] and [12, Theorem 14.2], we obtain

$$\begin{aligned}{} & {} \left[ \int _{\mathbb {T}^d} \varrho _h\phi \,\textrm{d}x \right] _{t=0}^\tau \nonumber \\ {}{} & {} \quad = \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \left( \varrho _h\partial _t \phi + \varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x\phi \right) \,\textrm{d}x \textrm{dt}\; + e_\varrho (\tau , \Delta t, h, \phi ), \end{aligned}$$
(2.18a)
$$\begin{aligned}{} & {} \left[ \int _{\mathbb {T}^d} \varrho _h\Pi _Q\varvec{u}_h\cdot \varvec{\phi } \,\textrm{d}x \right] _{t=0}^\tau \nonumber \\ {}{} & {} \quad = \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \left( \varrho _h\Pi _Q\varvec{u}_h\cdot \partial _t \varvec{\phi }+ \varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h: \nabla _x\varvec{\phi } \right) \,\textrm{d}x \textrm{dt}\nonumber \\ {}{} & {} \qquad + \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \big ( p_h \mathbb {I} - \mu \nabla _h\varvec{u}_h- \nu \textrm{div}_h\varvec{u}_h\big ): \nabla _x\varvec{\phi } \,\textrm{d}x \textrm{dt}\; +e_{\varvec{m}}^* (\tau , \Delta t, h, \phi ),\nonumber \\ \end{aligned}$$
(2.18b)

where \(e_{\varvec{m}}^*\) is controlled by

$$\begin{aligned}{} & {} \left|e_{\varvec{m}}^*(\tau , \Delta t, h, \varvec{\phi }) \right|\\{} & {} \quad \le {\left\{ \begin{array}{ll} C_{\varvec{m}} \big ( \Delta t+ h + h^{1+\varepsilon } + h^{1+\beta _M} \big )&{} \text{ for } \text{ the } \text{ FV } \text{ method, } \\ C_{\varvec{m}} \big ( \Delta t+h + h^{1+\varepsilon } + h^{1+\beta _M} + h^{1+\varepsilon + \beta _D } \big ) &{} \text{ for } \text{ the } \text{ MAC } \text{ method. } \end{array}\right. } \end{aligned}$$

In order to derive (2.15a) it suffices to realize that the time integral from \(\tau \) to \(t^{n+1}\) at the right-hand side of (2.18a) is of order \({\mathcal {O}}(\Delta t)\). Indeed

$$\begin{aligned}{} & {} \int _\tau ^{t^{n+1}} \int _{\mathbb {T}^d} \Big ( \varrho _h\partial _t \phi + \varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x\phi \Big ) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \le \big ( \Vert \partial _t\phi \Vert _{L^\infty L^\infty } \Vert \varrho _h^n\Vert _{L^\infty L^1} + \Vert \nabla _x\phi \Vert _{L^\infty L^\infty }\Vert \varrho _h^n \Pi _Q\varvec{u}_h^n\Vert _{L^\infty L^1} \big ) \int _\tau ^{t^{n+1}} 1 \textrm{dt}\lesssim \Delta t.\nonumber \\ \end{aligned}$$
(2.19)

Combining (2.18a) and (2.19) yields (2.15a).

Similarly, to get (2.15b) we need the following estimate

$$\begin{aligned}{} & {} \int _\tau ^{t^{n+1}} \int _{\mathbb {T}^d} \Big ( \varrho _h\Pi _Q\varvec{u}_h\cdot \partial _t \varvec{\phi }+ \big (\varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h+ p_h \mathbb {I} - \mu \nabla _h\varvec{u}_h- \nu \textrm{div}_h\varvec{u}_h\big ): \nabla _x\varvec{\phi }\Big ) \,\textrm{d}x \textrm{dt}\\{} & {} \quad \le \int _\tau ^{t^{n+1}} \Vert \varrho _h^n\Pi _Q\varvec{u}_h^n\Vert _{L^1(\mathbb {T}^d)} \Vert \partial _t\varvec{\phi }\Vert _{L^\infty (\mathbb {T}^d) } \textrm{dt}\\{} & {} \qquad +\int _\tau ^{t^{n+1}} \Vert \varrho _h^n \Pi _Q\varvec{u}_h^n \otimes \Pi _Q\varvec{u}_h^n + p_h^n \mathbb {I} \Vert _{L^1(\mathbb {T}^d)} \Vert \nabla _x\varvec{\phi }\Vert _{L^\infty (\mathbb {T}^d) } \textrm{dt}\\{} & {} \qquad +\int _\tau ^{t^{n+1}} \Vert \mu \nabla _h\varvec{u}_h^n + \nu \textrm{div}_h\varvec{u}_h^n \Vert _{L^1(\mathbb {T}^d)} \Vert \nabla _x\varvec{\phi }\Vert _{L^\infty (\mathbb {T}^d) } \textrm{dt}\\{} & {} \quad \le \Delta t\Vert \varrho _h\Pi _Q\varvec{u}_h\Vert _{L^\infty L^1} \Vert \partial _t\varvec{\phi }\Vert _{L^\infty L^\infty } +\Delta t\Vert \varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h+ p_h \ \Vert _{L^\infty L^1} \Vert \nabla _x\varvec{\phi }\Vert _{L^\infty L^\infty } \\{} & {} \qquad + \Vert \nabla _x\varvec{\phi }\Vert _{ L^\infty L^\infty } \Vert \mu \nabla _h\varvec{u}_h+ \nu \textrm{div}_h\varvec{u}_h\Vert _{L^2 L^1} \left( \int _\tau ^{t^{n+1}} 1^2\textrm{dt}\right) ^{1/2} \lesssim \sqrt{\Delta t}. \end{aligned}$$

Substituting the above estimate into (2.18b) we obtain (2.15b), which completes the proof. \(\square \)

Lemma 2.10

(Consistency formulation for a bounded numerical solution) Let the assumptions of Lemma 2.9 hold. Moreover, let \(\varrho _h\) and \(\varvec{u}_h\) be uniformly bounded, i.e., there exist positive constants \(\overline{\varrho }\) and \(\overline{u}\) such that

$$\begin{aligned} \varrho _h\le \overline{\varrho } \text{ and } \left|\varvec{u}_h \right| \le \overline{u}. \end{aligned}$$
(2.20)

Then for all \(\tau \in (0,T)\), \(\phi \in L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d))\), \( \partial _t ^2 \phi \in L^\infty ((0,T) \times \mathbb {T}^d)\) and \(\varvec{\phi }\in L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d; \mathbb {R}^d))\), \( \partial _t ^2 \varvec{\phi }\in L^\infty ((0,T) \times \mathbb {T}^d; \mathbb {R}^d)\), there holds

$$\begin{aligned}{} & {} \left[ \int _{\mathbb {T}^d} \varrho _h\phi \,\textrm{d}x \right] _{t=0}^\tau \nonumber \\ {}{} & {} \quad = \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h\partial _t \phi + \varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x\phi \right) \,\textrm{d}x \textrm{dt}\; + e_\varrho (\tau , \Delta t, h, \phi ), \end{aligned}$$
(2.21a)
$$\begin{aligned}{} & {} \left[ \int _{\mathbb {T}^d} \varrho _h\Pi _Q\varvec{u}_h\cdot \varvec{\phi } \,\textrm{d}x \right] _{t=0}^\tau \nonumber \\ {}{} & {} \quad = \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h\Pi _Q\varvec{u}_h\cdot \partial _t \varvec{\phi }+ \varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h: \nabla _x\varvec{\phi }+ p_h \textrm{div} _x\varvec{\phi } \right) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \qquad + \int _0^\tau \int _{\mathbb {T}^d} \varvec{u}_h\cdot ( \mu \Delta _x \varvec{\phi }+ \nu \nabla _x \textrm{div} _x\varvec{\phi }) \,\textrm{d}x \textrm{dt}\; +e_{\varvec{m}}(\tau , \Delta t, h, \varvec{\phi }), \end{aligned}$$
(2.21b)

where the consistency errors can be bounded as follows

$$\begin{aligned} \begin{aligned} \left|e_\varrho (\tau , \Delta t, h, \phi ) \right| \le C_\varrho (\Delta t+ h ), \quad \left|e_{\varvec{m}}(\tau , \Delta t, h, \varvec{\phi }) \right| \le C_{\varvec{m}} ( \Delta t+ h ) \end{aligned} \end{aligned}$$
(2.21c)

Here, the constant \(C_\varrho \) depends on

$$\begin{aligned} \overline{\varrho }, \overline{u}, E_0, T,\Vert \phi \Vert _{ L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d)) },\, \Vert \partial _t^2 \phi \Vert _{L^\infty ((0,T) \times \mathbb {T}^d) }, \end{aligned}$$

and \(C_{\varvec{m}}\) depends on

$$\begin{aligned} \overline{\varrho },\overline{u}, E_0, T, \Vert \varvec{\phi }\Vert _{ L^\infty (0,T; W^{2,\infty }(\mathbb {T}^d; \mathbb {R}^d)) },\, \Vert \varvec{\phi }\Vert _{ L^2(0,T;W^{3,2}(\mathbb {T}^d; \mathbb {R}^d)) }, \Vert \partial _t^2 \varvec{\phi }\Vert _{L^\infty ((0,T) \times \mathbb {T}^d; \mathbb {R}^d) }. \end{aligned}$$

Proof

We will present the proof for the FV method, the proof for the MAC method is analogous. First, we denote the errors of the inviscid fluxes as

(2.22)
(2.23)

Analogously as in the proof of [12, Theorem 11.3] we get

$$\begin{aligned} |e_1| \le c(\Vert \phi \Vert _{L^\infty W^{2, \infty }}) h \Vert \varrho _h\Vert _{L^2L^2}\ \ \text{ and } \ \ |e_2| \le c(\Vert \varvec{\phi }\Vert _{L^\infty W^{2, \infty }}) h \Vert \varrho _h\varvec{u}_h\Vert _{L^2L^2}. \end{aligned}$$

In view of assumption (2.20) the errors \(e_1\) and \(e_2\) are controlled by

$$\begin{aligned} \begin{aligned}&|e_1| \le c(\Vert \phi \Vert _{L^\infty W^{2, \infty }}) h \Vert \varrho _h\Vert _{L^2L^2} \le c(\Vert \phi \Vert _{L^\infty W^{2, \infty }}, \overline{\varrho }) h, \\ {}&|e_2| \le c(\Vert \varvec{\phi }\Vert _{L^\infty W^{2, \infty }}) h \Vert \varrho _h\varvec{u}_h\Vert _{L^2L^2} \le c(\Vert \varvec{\phi }\Vert _{L^\infty W^{2, \infty }}, \overline{\varrho }, \overline{u}) h. \end{aligned} \end{aligned}$$
(2.24)

Now, summing up (2.22) and (2.17) with \(r_h =\varrho _h\), and recalling the estimates (2.19) and (2.24) implies (2.21a). Moreover, summing up (2.23) and (2.17) with \(r_h =\varrho _h\varvec{u}_h\) we get

$$\begin{aligned} \left[ \int _{\mathbb {T}^d} \varrho _h\varvec{u}_h\cdot \varvec{\phi } \,\textrm{d}x \right] _0^{\tau }= & {} \int _0^\tau \int _{\mathbb {T}^d} \varrho _h\varvec{u}_h\cdot \partial _t \varvec{\phi }+ \big (\varrho _h\varvec{u}_h\otimes \varvec{u}_h+ p_h \mathbb {I} \big ): \nabla _x\varvec{\phi }\nonumber \\{} & {} + \varvec{u}_h\cdot (\mu \Delta _x \varvec{\phi }+ \nu \nabla _x \textrm{div} _x\varvec{\phi }) \,\textrm{d}x \textrm{dt}+ e_2 +e_3 +e_4, \end{aligned}$$
(2.25)

where \(e_2\) is given in (2.23) and \(e_3,e_4,e_5\) read

$$\begin{aligned} e_3&= - \mu \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \left( \varvec{u}_h\cdot \Delta _x \varvec{\phi }+ \nabla _{{{\mathcal {D}}}}\varvec{u}_h: \nabla _{{{\mathcal {D}}}}\Pi _Q\varvec{\phi } \right) \,\textrm{d}x \textrm{dt}, \\ e_{4}&= - \nu \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \left( \varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{\phi }+ \textrm{div}_h\varvec{u}_h\textrm{div}_h\Pi _Q\varvec{\phi } \right) \,\textrm{d}x \textrm{dt}, \\ e_5&= \int _\tau ^{t^{n+1}} \int _{\mathbb {T}^d} \left( \varrho _h\Pi _Q\varvec{u}_h\cdot \partial _t \varvec{\phi }+ \big (\varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h+ p_h \mathbb {I}\big ): \nabla _x\varvec{\phi }+ \varvec{u}_h\cdot (\mu \Delta _x \varvec{\phi }+ \nu \nabla _x \textrm{div} _x\varvec{\phi }) \right) \,\textrm{d}x\\ {}&\quad \times \textrm{dt}. \end{aligned}$$

Recalling (2.8c), (2.9b), (2.9d) and using Hölder’s inequality, we get

$$\begin{aligned} |e_3|&=\left| \mu \int _0^{t^{n+1}} \int _{\mathbb {T}^d} \nabla _{{{\mathcal {D}}}}\varvec{u}_h: ( \Pi _ {\mathcal {E}} \nabla _x\varvec{\phi }- \nabla _{{{\mathcal {D}}}}\Pi _Q\varvec{\phi }) \,\textrm{d}x\textrm{dt}\right| \lesssim c(\Vert \varvec{\phi }\Vert _{L^2W^{2,2}}, E_0 ) h. \end{aligned}$$

Similarly, recalling (2.8d), (2.9a), (2.9c) and Hölder’s inequality, we get

$$\begin{aligned} |e_4|&= \nu \left|\int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h \textrm{div} _x\varvec{u}+ \varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u}- \underbrace{ \big ( \Pi _{\epsilon } \textrm{div} _x\varvec{u}\; \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h+ \left\{ \!\!\left\{ \varvec{u}_h\right\} \!\!\right\} \cdot \nabla _x \textrm{div} _x\varvec{u}\big )}_{=0} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \nu \bigg | \int _0^\tau \int _{\mathbb {T}^d} \Big ( \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h( \textrm{div} _x\varvec{u}- \Pi _{\epsilon } \textrm{div} _x\varvec{u}) + (\varvec{u}_h- \left\{ \!\!\left\{ \varvec{u}_h\right\} \!\!\right\} ) \cdot \nabla _x \textrm{div} _x\varvec{u}\Big ) \,\textrm{d}x\textrm{dt} \bigg | \\ {}&\le h \left( \Vert \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h\Vert _{L^2L^2}+ \Vert \nabla _{{{\mathcal {D}}}}\varvec{u}_h\Vert _{L^2L^2} \right) \Vert \varvec{u}\Vert _{L^2 W^{2,2}}. \end{aligned}$$

We are left with the estimate of \(e_5\), which can be controlled due to Hölder’s inequality.

Consequently, collecting the estimates of \(e_2\), \(e_3\), \(e_4\) and \(e_5\) we observe that (2.21b) follows from (2.25), which completes the proof. \(\square \)

3 Error estimates

This section is the heart of the paper. We prove the main result – the convergence rates for the FV (2.10) and MAC (2.11) schemes. If, in addition, the numerical solutions are uniformly bounded, the convergence rates can be improved to the first order.

Theorem 3.1

(Convergence rates) Let \(\gamma > 1\) and the initial data \((\varrho _0, \varvec{u}_0)\) satisfy

$$\begin{aligned} \varrho _0 \in W^{k,2}({\mathbb {T}^d}),\ \varrho _0 > 0 \text{ in } \mathbb {T}^d, \qquad \varvec{u}_0 \in W^{k,2}(\mathbb {T}^d; \mathbb {R}^d), \quad k \ge 6. \end{aligned}$$

Suppose that the Navier–Stokes system (1.1) admits a classical solution \((\varrho ,\varvec{u})\) defined on \([0,T] \times \mathbb {T}^d\), with the initial data \((\varrho _0, \varvec{u}_0).\) Further, let \((\varrho _h, \varvec{u}_h)\) be a numerical solution obtained either by the FV scheme (2.10) or by the MAC scheme (2.11) emanating from the projected initial data \((\varrho _h^0, \varvec{u}_h^0)\).

Then there exists a positive number

$$\begin{aligned} c=c( T, \Vert (\varrho _0, \varvec{u}_0)\Vert _{W^{k,2}(\mathbb {T}^d; \mathbb {R}^{d+1})}, \inf \varrho _0, \Vert (\varrho , \varvec{u})\Vert _{C([0,T]\times \mathbb {T}^d; \mathbb {R}^{d+1})}) \end{aligned}$$

such that

$$\begin{aligned} \begin{aligned}&\sup _{0\le t \le T} {\mathfrak {E}}(\varrho _h,\varvec{u}_h | \varrho , \varvec{u}) +\mu \int _0^T \int _{\mathbb {T}^d} | \nabla _h\varvec{u}_h- \nabla _x\varvec{u}|^2 \,\textrm{d}x \textrm{dt}+ \nu \int _0^T \int _{\mathbb {T}^d} |\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u}|^2 \,\textrm{d}x \textrm{dt}\\&\le c ( h^A + \sqrt{\Delta t}), \end{aligned} \end{aligned}$$
(3.1)
$$\begin{aligned} \begin{aligned}&\Vert \varrho _h-\varrho \Vert _{L^\infty L^\gamma } + \Vert \varrho _h \varvec{u}_h - \varrho \varvec{u}\Vert _{L^\infty L^\frac{2 \gamma }{\gamma +1}} \lesssim c(\sqrt{\Delta t} +h)^{1/2} + c(\sqrt{\Delta t} +h^A)^{1/\gamma }&\quad \text{ for } \gamma \le 2, \\ {}&\Vert \varrho _h- \varrho \Vert _{L^\infty L^2} + \Vert \varrho _h \varvec{u}_h - \varrho \varvec{u}\Vert _{L^\infty L^\frac{2 \gamma }{\gamma +1}} \lesssim c(\sqrt{\Delta t} +h^A)^{1/2}&\quad \text{ for } \gamma > 2, \end{aligned} \end{aligned}$$
(3.2)

and

$$\begin{aligned} \Vert \varvec{u}_h- \varvec{u}\Vert _{L^2 L^2} \lesssim c(\sqrt{\Delta t} +h^A)^{1/2}. \end{aligned}$$
(3.3)

The convergence rate A reads

$$\begin{aligned} A= {\left\{ \begin{array}{ll} A_{FV}:= \min \left\{ 1, 1+\varepsilon , 1+\beta _D, 1+\beta _M \right\} &{} \text{ for } \text{ the } \text{ FV } \text{ method }, \\ A_{MAC}:= \min \left\{ 1, 1+\varepsilon , 1+\beta _D, 1+\beta _M, 1+\varepsilon +\beta _D \right\} &{} \text{ for } \text{ the } \text{ MAC } \text{ method }. \end{array}\right. }\nonumber \\ \end{aligned}$$
(3.4)

Here the constants \(\beta _D\) and \(\beta _M\) are given in (2.15d).

Remark 3

Let us discuss the obtained convergence rate \({\mathcal {O}}(h^A)\) for the choice \(\Delta t=h\) and different values of \(\gamma >1\), \(d=2,3.\)

  • For the case \(d=2\), we obtain the following convergence rate A:

    • Let \(\gamma \ge 2\). Then for any \(\varepsilon \ge 0\) both numerical methods have the first-order convergence rate, i.e. \(A=1.\)

    • Let \(\gamma \in (1,2)\). The convergence rates are different for the FV and MAC schemes.

      • * \(A_{FV}= \min \left\{ 1- \frac{5+3\varepsilon }{6\gamma }, 1, 1+\varepsilon \right\} \). Choosing the optimal value of \(\varepsilon \), \(\varepsilon = - \frac{5}{3+6\gamma }\in (-\frac{5}{9}, -\frac{1}{3})\), the convergence rate \(A_{FV}=1 + \varepsilon \) varies between \(\frac{4}{9}\) for \(\gamma \searrow 1\) and \(\frac{2}{3}\) for \(\gamma \nearrow 2.\)

      • * \(A_{MAC}= \min \left\{ 1- \frac{5+3\varepsilon }{6\gamma }, 1, 1+\varepsilon , 1+\varepsilon -\frac{5+3\varepsilon }{6\gamma } \right\} \) reaches its maximum value \(\frac{6\gamma -5}{6\gamma }>0\) at \(\varepsilon =0\). Thus, the convergence rate varies between \(\frac{1}{6}\) for \(\gamma \searrow 1\) and \(\frac{7}{12}\) for \(\gamma \nearrow 2.\)

  • For the case \(d=3\), we obtain the following convergence rate A:

    • Let \(\gamma \ge 3\). Then for any \(\varepsilon \ge 0\) both methods have first-order convergence rates, i.e. \(A=1\).

    • Let \(\gamma \in [2,3)\). Then for any \(\varepsilon \ge \frac{2\gamma -3}{\gamma }\) we have \(A= \frac{2\gamma -3}{\gamma }\) and the convergence rate varies between \(\frac{1}{2}\) for \(\gamma = 2\) and 1 for \(\gamma \nearrow 3\).

    • Let \(\gamma \in (1,2)\).

      • * \(A_{FV}= \min \left\{ 1- \frac{2+\varepsilon }{2\gamma }, 1, 1+\varepsilon \right\} \). Choosing an optimal value of \(\varepsilon ,\) \(\varepsilon = - \frac{ 2}{1+2\gamma }\in (-\frac{2}{3}, -\frac{2}{5})\), \(A_{FV} = 1+\varepsilon \) and varies between \(\frac{1}{3}\) for \(\gamma \searrow 1\) and \(\frac{3}{5}\) for \(\gamma \nearrow 2.\)

      • * \(A_{MAC}= \min \left\{ 1- \frac{2+\varepsilon }{2\gamma }, 1, 1+\varepsilon , 1+\varepsilon -\frac{2+\varepsilon }{2\gamma } \right\} \) reaches its maximum value \(\frac{\gamma -1}{\gamma } > 0\) at \(\varepsilon =0\). Note that \(A_{MAC}\) varies between 0 when \(\gamma \searrow 1\) and \(\frac{1}{2}\) when \(\gamma \nearrow 2.\)

Remark 4

In view of the above results, the convergence rates available in the literature, see e.g. [14, 15, 24], are not optimal. Indeed, for \(d=3\) and \(\gamma =\frac{3}{2}\), they degenerate to 0. Moreover, no error analysis is available for \(\gamma < \frac{3}{2}.\) Our approach yields error estimates also for \(\gamma \in (1, \frac{3}{2}].\) In addition, we have better convergence rates, e.g., for \(d=3\) and \(\gamma =\frac{3}{2}\), where the convergence errors are \({\mathcal {O}}(h^{\frac{3}{4} })\) and \({\mathcal {O}}(h^{\frac{1}{3} })\) for the FV and MAC schemes, respectively.

Proof of Theorem 3.1

First, by a straightforward but lengthy calculation, see Appendix D, we observe the following relative energy inequality

$$\begin{aligned} \begin{aligned}&\left[ {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \right] _0^\tau + \int _0^\tau \int _{\mathbb {T}^d} \left( \mu \left| \nabla _h\varvec{u}_h \right|^2 + \nu \left|\textrm{div}_h\varvec{u}_h \right|^2 \right) \,\textrm{d}x \textrm{dt}\\ {}&\le \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h \partial _t\frac{\left|\varvec{u} \right|^2}{2} + \varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x\frac{ \left|\varvec{u} \right|^2}{2} \right) \,\textrm{d}x\textrm{dt}\; + e_\varrho \left( \tau , \Delta t, h, \left|\varvec{u} \right|^2/2 \right) \\ {}&- \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h \partial _t {P} '(\varrho ) + \varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x {P} '(\varrho ) \right) \,\textrm{d}x \; - e_\varrho ( \tau , \Delta t, h, {P} '(\varrho ) ) \\ {}&- \int _0^\tau \int _{\mathbb {T}^d} \left( \varrho _h\Pi _Q\varvec{u}_h\cdot \partial _t\varvec{u}+ \varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h: \nabla _x\varvec{u}+ p_h \textrm{div} _x\varvec{u} \right) \,\textrm{d}x \textrm{dt}\\ {}&+ \int _0^\tau \int _{\mathbb {T}^d} \left( \mu \nabla _h\varvec{u}_h: \nabla _x\varvec{u}+ \nu \textrm{div}_h\varvec{u}_h \textrm{div} _x\varvec{u} \right) \,\textrm{d}x \textrm{dt}\; + {e_{\varvec{m}} (\tau , \Delta t, h,-\varvec{u})} \\ {}&+ \int _0^\tau \int _{\mathbb {T}^d} \partial _t\big ( \varrho {P} '(\varrho ) - {P} (\varrho ) \big ) \,\textrm{d}x \textrm{dt}. \end{aligned} \end{aligned}$$
(3.5)

Next, we observe the following identities

$$\begin{aligned}\begin{aligned}&\varrho _h\Pi _Q\varvec{u}_h\cdot \nabla _x\frac{\left|\varvec{u} \right|^2}{2} - \varrho _h\Pi _Q\varvec{u}_h\otimes \Pi _Q\varvec{u}_h: \nabla _x\varvec{u}\\ {}&= - \varrho _h(\Pi _Q\varvec{u}_h-\varvec{u}) \otimes (\Pi _Q\varvec{u}_h-\varvec{u}): \nabla _x\varvec{u}-\varrho _h(\Pi _Q\varvec{u}_h-\varvec{u}) \cdot (\varvec{u}\cdot \nabla _x\varvec{u}), \end{aligned} \\ {P} ''(\varrho ) =\frac{1}{\varrho } p'(\varrho ), \quad \varrho {P} '(\varrho ) - {P} (\varrho ) = p(\varrho ), \quad \partial _t( \varrho {P} '(\varrho ) - {P} (\varrho )) = \partial _tp(\varrho ). \end{aligned}$$

Then by substituting the above equalities into (3.5) and denoting

$$\begin{aligned} e_S= e_\varrho \left( \tau , \Delta t, h,\left|\varvec{u} \right|^2/2\right) - e_\varrho (\tau , \Delta t, h, {P} '(\varrho ) ) + e_{\varvec{m}} (\tau , \Delta t, h,-\varvec{u}), \end{aligned}$$

we obtain

$$\begin{aligned}{} & {} \left[ {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \right] _0^{\tau } + \int _0^\tau \int _{\mathbb {T}^d} \left( \mu \left| \nabla _h\varvec{u}_h- \nabla _x\varvec{u} \right|^2 + \nu \left|\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u} \right|^2 \right) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \le e_S + \int _0^\tau \int _{\mathbb {T}^d} \varrho _h(\varvec{u}- \Pi _Q\varvec{u}_h) \cdot ( \partial _t\varvec{u}+ \varvec{u}\cdot \nabla _x\varvec{u}) \,\textrm{d}x \textrm{dt}\nonumber \\{} & {} \quad - \int _0^\tau \int _{\mathbb {T}^d} \varrho _h(\Pi _Q\varvec{u}_h-\varvec{u}) \otimes (\Pi _Q\varvec{u}_h-\varvec{u}): \nabla _x\varvec{u} \,\textrm{d}x\textrm{dt} \nonumber \\{} & {} \quad + \mu \int _0^\tau \int _{\mathbb {T}^d}\left( \left| \nabla _x\varvec{u} \right|^2 - \nabla _h\varvec{u}_h: \nabla _x\varvec{u} \right) \,\textrm{d}x\textrm{dt}\nonumber \\{} & {} \quad + \nu \int _0^\tau \int _{\mathbb {T}^d}\left( \left| \textrm{div} _x\varvec{u} \right| ^2 - \textrm{div}_h\varvec{u}_h \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \nonumber \\{} & {} \quad + \int _0^\tau \int _{\mathbb {T}^d}\left( \partial _tp(\varrho ) - \varrho _h\frac{ \partial _tp(\varrho )}{\varrho } - \varrho _h\Pi _Q\varvec{u}_h\cdot \frac{ \nabla _xp(\varrho )}{\varrho } - p_h \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt}. \end{aligned}$$
(3.6)

As \((\varrho ,\varvec{u})\) satisfies the Navier–Stokes system (1.1), we know that

$$\begin{aligned} \varrho ( \partial _t\varvec{u}+ \varvec{u}\cdot \nabla _x\varvec{u}) = \mu \Delta _x \varvec{u}+ \nu \nabla _x \textrm{div} _x\varvec{u}- \nabla _xp(\varrho ).\end{aligned}$$

Substituting this equality into (3.6) we get

$$\begin{aligned}&\left[ {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \right] _0^{\tau } + \int _0^\tau \int _{\mathbb {T}^d}\left( \mu \left| \nabla _h\varvec{u}_h- \nabla _x\varvec{u} \right|^2 + \nu \left|\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u} \right|^2 \right) \,\textrm{d}x\textrm{dt} \\ {}&\quad \le e_S + \int _0^\tau \int _{\mathbb {T}^d} (\varrho _h-\varrho ) (\varvec{u}- \Pi _Q\varvec{u}_h) \cdot ( \partial _t\varvec{u}+ \varvec{u}\cdot \nabla _x\varvec{u}) \,\textrm{d}x\textrm{dt}, \\&\qquad - \int _0^\tau \int _{\mathbb {T}^d} \varrho _h(\Pi _Q\varvec{u}_h-\varvec{u}) \otimes (\Pi _Q\varvec{u}_h-\varvec{u}) : \nabla _x\varvec{u} \,\textrm{d}x\textrm{dt} , \\&\qquad + \mu \int _0^\tau \int _{\mathbb {T}^d}\left( \left| \nabla _x\varvec{u} \right|^2 - \nabla _h\varvec{u}_h: \nabla _x\varvec{u}+(\varvec{u}- \Pi _Q\varvec{u}_h) \cdot \Delta _x \varvec{u} \right) \,\textrm{d}x\textrm{dt} \\&\qquad + \nu \int _0^\tau \int _{\mathbb {T}^d}\left( \left| \textrm{div} _x\varvec{u} \right| ^2 - \textrm{div}_h\varvec{u}_h \textrm{div} _x\varvec{u}+(\varvec{u}- \Pi _Q\varvec{u}_h) \cdot \nabla _x \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \\&\qquad + \int _0^\tau \int _{\mathbb {T}^d}\left( \frac{\varrho -\varrho _h}{\varrho } \partial _tp(\varrho ) - \frac{\varrho _h}{\varrho }\Pi _Q\varvec{u}_h\cdot \nabla _xp(\varrho ) - p_h \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt}\\ {}&\qquad - \int _0^\tau \int _{\mathbb {T}^d} (\varvec{u}- \Pi _Q\varvec{u}_h) \cdot \nabla _xp(\varrho ) \,\textrm{d}x\textrm{dt}. \end{aligned}$$

Rearranging the terms on the right-hand side, we arrive at

$$\begin{aligned}{} & {} \left[ {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \right] _0^\tau + \int _0^\tau \int _{\mathbb {T}^d}\left( \mu \left| \nabla _h\varvec{u}_h- \nabla _x\varvec{u} \right|^2 + \nu \left|\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u} \right|^2 \right) \,\textrm{d}x\textrm{dt}\\{} & {} \quad \le e_S + \sum _{i=1}^5 R^E_i, \end{aligned}$$

where the integrals \(R^E_i, i=1,\ldots ,5\), read

$$\begin{aligned} R^E_1&= \int _0^\tau \int _{\mathbb {T}^d} (\varrho _h- \varrho ) (\varvec{u}- \Pi _Q\varvec{u}_h) \cdot ( \partial _t\varvec{u}+ \varvec{u}\cdot \nabla _x\varvec{u}+ \frac{ \nabla _xp(\varrho )}{\varrho }) \,\textrm{d}x\textrm{dt} \\ {}&= \int _0^\tau \int _{\mathbb {T}^d} (\varrho _h-\varrho ) (\varvec{u}- \Pi _Q\varvec{u}_h) \cdot \frac{ \textrm{div} _x \mathbb {S}( \nabla _x\varvec{u})}{\varrho } \,\textrm{d}x\textrm{dt} \\ R^E_2&= - \int _0^\tau \int _{\mathbb {T}^d} \varrho _h(\Pi _Q\varvec{u}_h-\varvec{u}) \otimes (\Pi _Q\varvec{u}_h-\varvec{u}) : \nabla _x\varvec{u} \,\textrm{d}x\textrm{dt} , \\ R^E_3&= - \mu \int _0^\tau \int _{\mathbb {T}^d}\left( \nabla _h\varvec{u}_h: \nabla _x\varvec{u}+ \Pi _Q\varvec{u}_h\cdot \Delta _x \varvec{u} \right) \,\textrm{d}x\textrm{dt}, \\ R^E_4&= - \nu \int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div}_h\varvec{u}_h \textrm{div} _x\varvec{u}+ \Pi _Q\varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt}, \\ R^E_5&= - \int _0^\tau \int _{\mathbb {T}^d} \big (p_h - p'(\varrho ) (\varrho _h- \varrho ) -p(\varrho ) \big ) \textrm{div} _x\varvec{u} \,\textrm{d}x\textrm{dt} . \end{aligned}$$

Next, for \(i=1,\ldots , 5\) we analyze \(R^E_i\) such that it can be controlled either by the relative energy or the mesh parameter h.

Term \(R^E_1\). Applying Hölder’s inequality and Lemma B.4 we obtain

$$\begin{aligned} \left|R^E_1 \right|&\le \frac{1}{{\underline{r}}} \Vert \textrm{div} _x \mathbb {S}( \nabla _x\varvec{u})\Vert _{L^\infty ( (0,T)\times \mathbb {T}^d)}\\ {}&\quad \times \left( C_0 \int _0^\tau {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \textrm{dt} + C_1 \delta \Vert \nabla _h\varvec{u}_h- \nabla _x\varvec{u}\Vert _{L^2}^2 + C_2 \delta h^2\right) \\ {}&= C_0^* \int _0^\tau {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \textrm{dt} + C_1^* \delta \Vert \nabla _h\varvec{u}_h- \nabla _x\varvec{u}\Vert _{L^2}^2 + C_2^* \delta h^2, \end{aligned}$$

where \(C_0^*>0\) depends on \(\Vert \varvec{u}\Vert _{L^\infty W^{2,\infty }}\), \(\Vert \varrho \Vert _{C([0,T] \times \mathbb {T}^d)}, M, E_0, \gamma \), \(\delta \), and \({\underline{r}} = \min _{[0,T] \times \mathbb {T}^d} \varrho \);

\( C_1^*>0\) depends on \(\Vert \varvec{u}\Vert _{L^\infty W^{2,\infty }}\), \( M, E_0\), and \(\gamma \);

\(C_2^*>0\) depends on \(\Vert \varvec{u}\Vert _{L^\infty W^{2,\infty }}\), M, \(E_0, \gamma \), and \(\Vert \nabla _x\varvec{u}\Vert _{L^\infty ( (0,T)\times \mathbb {T}^d)} \).

Term \(R^E_2\). Thanks to Hölder’s inequality we observe the following estimate.

$$\begin{aligned} \left|R^E_2 \right| \le C \int _0^\tau {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \textrm{dt}, \end{aligned}$$

where C depends on \(\Vert \nabla _x\varvec{u}\Vert _{L^\infty ( (0,T)\times \mathbb {T}^d)} \).

Term \(R^E_3\). We analyze the third term \(R^E_3\) in two cases.

First, we consider the case of the FV scheme. In this case \(\varvec{u}_h\in \textbf{Q}_h\), \( \nabla _h\varvec{u}_h= \nabla _{{{\mathcal {D}}}}\varvec{u}_h\) and \(\Pi _Q\varvec{u}_h= \varvec{u}_h\). Thus,

$$\begin{aligned} \left| R^E_3 \right|&= \mu \left| \int _0^\tau \int _{\mathbb {T}^d}\left( \nabla _h\varvec{u}_h: \nabla _x\varvec{u}+ \Pi _Q\varvec{u}_h\cdot \Delta _x \varvec{u} \right) \,\textrm{d}x\textrm{dt} \right|\\ {}&= \mu \left| \int _0^\tau \int _{\mathbb {T}^d}\left( \nabla _{{{\mathcal {D}}}}\varvec{u}_h: \nabla _x\varvec{u}+ \varvec{u}_h\cdot \textrm{div} _{\mathcal {T}}^\textbf{W} \Pi _ {\mathcal {E}} \nabla _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \mu \left| \int _0^\tau \int _{\mathbb {T}^d} \nabla _{{{\mathcal {D}}}}\varvec{u}_h: ( \nabla _x\varvec{u}- \Pi _ {\mathcal {E}} \nabla _x\varvec{u}) \,\textrm{d}x\textrm{dt} \right| \le \mu h \Vert \nabla _h\varvec{u}_h\Vert _{L^2L^2} \Vert \varvec{u}\Vert _{L^2 W^{2,2}} , \end{aligned}$$

where we have used the equality (2.4), the integration by parts formula (2.3a), and the estimate (2.9b).

Second, we consider the case of \(\varvec{u}_h\in \textbf{W}_h\) obtained by the MAC scheme. In this case, \( \nabla _h\varvec{u}_h= \nabla _{{{\mathcal {B}}}}\varvec{u}_h\) and the term \(R^E_3\) can be estimated in the following way

$$\begin{aligned} \left| R^E_3 \right|&= \mu \left| \int _0^\tau \int _{\mathbb {T}^d}\left( \nabla _h\varvec{u}_h: \nabla _x\varvec{u}+ \Pi _Q\varvec{u}_h\cdot \Delta _x \varvec{u} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \mu \left| \int _0^\tau \sum _{i=1}^d\sum _{j=1}^d\sum _{\epsilon = D_\sigma |D_{\sigma '} \in {\widetilde{{\mathcal {E}}}}_{j,i}} \int _{D_\epsilon } \eth _{{\mathcal {B}}_{j,i}} u_{j,h} \left( \partial _i u_j - \frac{ ( \Pi _ {\mathcal {E}}^{(i)} \partial _i u_j)_{D_\sigma } +( \Pi _ {\mathcal {E}}^{(i)} \partial _i u_j)_{D_{\sigma '}} }{2} \right) \,\textrm{d}x \textrm{dt} \right| \\ {}&\le \mu h \Vert \nabla _h\varvec{u}_h\Vert _{L^2L^2} \Vert \varvec{u}\Vert _{L^2 W^{2,2}} , \end{aligned}$$

where we have applied (2.8a), Hölder’s inequality and the estimate (2.9b).

Consequently, we have for both cases

$$\begin{aligned} \left| R^E_3 \right| \le Ch, \end{aligned}$$

where the constant C depends on \(\mu ,\) the initial energy \(E_0\) and \(\Vert \varvec{u}\Vert _{L^2 W^{2,2}}\).

Term \(R^E_4\). We analyze the term \(R^E_4\) also in two cases.

First, for \(\varvec{u}_h\in \textbf{Q}_h\) obtained by the FV method, we have \( \textrm{div}_h\varvec{u}_h= \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h\), \(\Pi _Q\varvec{u}_h=\varvec{u}_h\) and thus

$$\begin{aligned} \left|R^E_4 \right|&= \nu \left|\int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div}_h\varvec{u}_h \textrm{div} _x\varvec{u}+ \Pi _Q\varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \nu \left|\int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h \textrm{div} _x\varvec{u}+ \varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u}-\big ( \Pi _{\epsilon } \textrm{div} _x\varvec{u}\; \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h+ \left\{ \!\!\left\{ \varvec{u}_h\right\} \!\!\right\} \cdot \nabla _x \textrm{div} _x\varvec{u}\big ) \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \nu \bigg | \int _0^\tau \int _{\mathbb {T}^d} \Big ( \textrm{div} _{\mathcal {T}}^{Q}\varvec{u}_h( \textrm{div} _x\varvec{u}- \Pi _{\epsilon } \textrm{div} _x\varvec{u}) + (\varvec{u}_h- \left\{ \!\!\left\{ \varvec{u}_h\right\} \!\!\right\} ) \cdot \nabla _x \textrm{div} _x\varvec{u}\Big ) \,\textrm{d}x\textrm{dt} \bigg | \\ {}&\le h \left( \Vert \textrm{div}_h\varvec{u}_h\Vert _{L^2L^2}+ \Vert \nabla _h\varvec{u}_h\Vert _{L^2L^2} \right) \Vert \varvec{u}\Vert _{L^2 W^{2,2}}, \end{aligned}$$

where we have used the identity (2.8d), Hölder’s inequality, the estimates (2.9a) and (2.9c).

Second, for the case of \(\varvec{u}_h\in \textbf{W}_h\) we have

$$\begin{aligned} \left|R^E_4 \right|&= \nu \left|\int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div}_h\varvec{u}_h \textrm{div} _x\varvec{u}+ \Pi _Q\varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \nu \left| \int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h \textrm{div} _x\varvec{u}- \big ( \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h \Pi _{\epsilon } \textrm{div} _x\varvec{u}+ \varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u}\big ) + \Pi _Q\varvec{u}_h\cdot \nabla _x \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&= \nu \left| \int _0^\tau \int _{\mathbb {T}^d}\left( \textrm{div} _{\mathcal {T}}^\textbf{W}\varvec{u}_h( \textrm{div} _x\varvec{u}- \Pi _{\epsilon } \textrm{div} _x\varvec{u}) + (\Pi _Q\varvec{u}_h- \varvec{u}_h) \cdot \nabla _x \textrm{div} _x\varvec{u} \right) \,\textrm{d}x\textrm{dt} \right| \\ {}&\le \nu h \left( \Vert \textrm{div}_h\varvec{u}_h\Vert _{L^2L^2}+ \Vert \nabla _h\varvec{u}_h\Vert _{L^2L^2} \right) \Vert \varvec{u}\Vert _{L^2 W^{2,2}}, \end{aligned}$$

where (2.8b), Hölder’s inequality, the estimates (2.9a) and (2.9c) were applied.

Consequently, we have for both cases

$$\begin{aligned} \left| R^E_4 \right| \le Ch, \end{aligned}$$

where the constant C depends on \(\nu \), initial energy \(E_0\), and \(\Vert \varvec{u}\Vert _{L^2 W^{2,2}}\).

Term \(R^E_5\). The estimate of \(R^E_5\) is straightforward by applying Hölder’s inequality, i.e.,

$$\begin{aligned} \left|R^E_5 \right| \le C \int _0^\tau {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u}) \textrm{dt} , \end{aligned}$$

where C depends on \(\Vert \textrm{div} _x\varvec{u}\Vert _{L^\infty ((0,T)\times \mathbb {T}^d)}\).

Consequently, collecting the above estimates of \(R^E_i\) for \(i=1,\cdots , 5\), we find

$$\begin{aligned} \begin{aligned}&{\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u})(\tau ) + \int _0^\tau \int _{\mathbb {T}^d}\left( (\mu - C_1^* \delta ) \left| \nabla _h\varvec{u}_h- \nabla _x\varvec{u} \right|^2 + \nu \left|\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u} \right|^2 \right) \,\textrm{d}x\textrm{dt}\\&\qquad \le e_S + {\mathfrak {E}}(\varrho _h, \varvec{u}_h| r, \varvec{u})(0) + C_0^* \int _0^\tau {\mathfrak {E}}(\varrho _h, \varvec{u}_h| r, \varvec{u}) \textrm{dt} + C_2^* \delta h^2. \end{aligned} \end{aligned}$$
(3.7)

Applying the standard projection error estimates we get

$$\begin{aligned} {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u})(0) \le C h^2, \end{aligned}$$
(3.8)

where C depends on \(\Vert \varrho _0\Vert _{C}\) and \(\Vert \varvec{u}_0\Vert _{L^2 W^{1,2}}\).

Consequently, by choosing \(\delta < \frac{\mu }{C_1^*}\), substituting (3.8) into (3.7), using Gronwall’s lemma and recalling the consistency error (2.15c), we may infer that

$$\begin{aligned}{} & {} {\mathfrak {E}}(\varrho _h, \varvec{u}_h| \varrho , \varvec{u})(\tau ) + \int _0^\tau \int _{\mathbb {T}^d}\left( \left| \nabla _h\varvec{u}_h- \nabla _x\varvec{u} \right|^2 + \left|\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u} \right|^2 \right) \,\textrm{d}x\textrm{dt}\\ {}{} & {} \quad \le C e^{\frac{\tau C_0^*}{1-\Delta tC_0^*}} (\sqrt{\Delta t} + h^A) \end{aligned}$$

for \(\Delta t< \frac{1}{C_0^*}\). Here, the constant C depends on \(\Vert \varrho \Vert _{L^{\infty } W^{2,\infty } }, \Vert \varvec{u}\Vert _{L^{\infty } W^{2,\infty } } \) and the exponent A is given by (3.4).

Finally, we combine the above estimate with Lemmas C.1 and B.2 in order to obtain (3.2) and (3.3), respectively. Note that \(E_0\) and M are bounded by the norm \(\Vert (\varrho _0, \varvec{u}_0)\Vert _{W^{k,2}(\mathbb {T}^d; R^{d + 1})}.\) Due to Proposition 1.1 all terms depending on the norms of the exact solution \((\varrho ,\varvec{u})\) as well as \({\underline{r}}\) are bounded by a constant \(c=c( T, \Vert (\varrho _0, \varvec{u}_0)\Vert _{W^{k,2}(\mathbb {T}^d; R^{d + 1})}, \Vert (\varrho , \varvec{u})\Vert _{C([0,T]\times \mathbb {T}^d; R^{d + 1})})\) which finishes the proof. \(\square \)

Finally, we observe that under the assumption that the numerical solutions \((\varrho _h,\varvec{u}_h)\) are uniformly bounded, the above error estimates can be improved. Indeed, applying Lemmas 2.10, C.1, and B.2 we derive the first-order error rate.

Theorem 3.2

(Error rates for bounded numerical solutions) In addition to the hypotheses of Theorem 3.1, let the numerical solution \((\varrho _h, \varvec{u}_h)\) be uniformly bounded,

$$\begin{aligned} \Vert \varrho _h\Vert _{L^\infty ((0,T) \times \mathbb {T}^d)} \le \overline{\varrho } \quad \text{ and } \quad \Vert \varvec{u}_h\Vert _{L^\infty ((0,T) \times \mathbb {T}^d; \mathbb {R}^d)} \le \overline{u}. \end{aligned}$$
(3.9)

Then there exists a positive number

$$\begin{aligned} c=c \left( T, \Vert ( \varrho _0, \varvec{u}_0)\Vert _{W^{k,2}(\mathbb {T}^d; \mathbb {R}^{d +1})}, \inf {\varrho _0}, \overline{\varrho }, \overline{u}, \right) \end{aligned}$$

such that

$$\begin{aligned} \begin{aligned}&\sup _{0\le t \le \tau } {\mathfrak {E}}(\varrho _h,\varvec{u}_h | \varrho , \varvec{u}) +\mu \int _0^\tau \int _{\mathbb {T}^d} | \nabla _h\varvec{u}_h- \nabla _x\varvec{u}|^2 \,\textrm{d}x\textrm{dt} + \nu \int _0^\tau \int _{\mathbb {T}^d} |\textrm{div}_h\varvec{u}_h- \textrm{div} _x\varvec{u}|^2 \,\textrm{d}x\textrm{dt} \\&\le c ( h + \Delta t) \end{aligned} \end{aligned}$$

for all \(\tau \in [0,T]\), and

$$\begin{aligned} \Vert \varrho _h- \varrho \Vert _{L^\infty L^2} + \Vert \varrho _h \varvec{u}_h - \varrho \varvec{u}\Vert _{L^\infty L^2} + \Vert \varvec{u}_h-\varvec{u}\Vert _{L^2L^2} \lesssim c(\Delta t^\frac{1}{2} + h^\frac{1}{2}). \end{aligned}$$

4 Conclusion

In this paper we have presented improved error estimates for two well-known numerical methods applied to compressible Navier–Stokes equations. Specifically, we consider the upwind finite volume method and the Marker-and-Cell (MAC) method with implicit time discretization and piecewise constant approximation in space. However, the approach presented in the paper can be applied also to other well-known numerical methods for compressible Navier–Stokes equations.

The novelty of our approach lies in the use of a continuous form of relative energy inequality combined with a refined consistency analysis. Thus, following the framework of the Lax equivalence theorem it suffices to show the (energy) stability, cf. Lemma 2.8, and the consistency of a numerical scheme, cf. Lemma 2.9, in order to obtain the convergence rates for the scheme. Indeed, consistency errors directly yield global errors in the relative energy. To obtain the corresponding error estimates we only assume that the initial data are sufficiently regular and that a strong solution exists globally in time. The error estimates presented in Theorem 3.1 improve the results already presented in the literature [14, 15, 24], see Remarks 2, 3 for a detailed discussion. In particular, our error estimates hold for the full range of the adiabatic coefficient \(\gamma > 1.\)

Moreover, we have considered a natural hypothesis on uniformly bounded numerical solutions and proved that the error estimates can be further improved, cf. Theorem 3.2. Indeed, we prove that both numerical methods converge with the first-order in time and mesh parameter in terms of the relative energy and with the half order in the \(L^\infty (0,T; L^2(\mathbb {T}^d))\)-norm for the density and momentum, as well as in the \(L^2((0,T) \times \mathbb {T}^d)\)-norm for the velocity.