Abstract
The present paper contributes to the ongoing programme of quantification of isomorphic Banach space theory focusing on the Hagler–Stegall characterisation of dual spaces containing complemented copies of \(L_{1}\). As a corollary, we obtain the following quantitative version of the Hagler–Stegall theorem asserting that for a Banach space X, the following statements are equivalent:
-
X contains almost isometric contains almost isometric copies of \((\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}\);
-
for all \(\varepsilon >0\), \(X^{*}\) contains a \((1+\varepsilon )\)-complemented, \((1+\varepsilon )\)-isomorphic copy of \(L_{1}\);
-
for all \(\varepsilon >0\), \(X^{*}\) contains a \((1+\varepsilon )\)-complemented, \((1+\varepsilon )\)-isomorphic copy of \(C[0,1]^{*}\).
Moreover, if X is separable, one may add the following assertion:
-
for all \(\varepsilon >0\), there exists a \((1+\varepsilon )\)-quotient map \(T:X\rightarrow C(\Delta )\) so that \(T^{*}[C(\Delta )^{*}]\) is \((1+\varepsilon )\)-complemented in \(X^{*}\), where \(\Delta \) is the Cantor set
Similar content being viewed by others
1 Introduction
In 1968, Pełczyński [17] showed that if a Banach space X contains an isomorphic copy of \(\ell _{1}\), then the dual space \(X^{*}\) contains an isomorphic copy of \(L_{1}\) and proved that the converse holds as well subject to a mild technical condition that was later removed by Hagler [7]. More precisely, the result stated that the isomorphic containment of \(\ell _1\) is equivalent to the following assertions: \(X^{*}\) contains a subspace isomorphic to \(L_{1}\), \(X^{*}\) contains a subspace isomorphic to \(C[0,1]^{*}\). When X is separable, these are further equivalent to the assertions: \(X^{*}\) contains a subspace isomorphic to \(\ell _1([0,1])\), and C[0, 1] is a quotient of X.
Shortly after, Hagler and Stegall [8] obtained a ‘complemented’ version of Pełczyński’s aforementioned classical work:
Theorem
(Hagler–Stegall). Let X be a Banach space. Then the following assertions are equivalent:
-
(1)
X contains a subspace isomorphic to \((\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}\);
-
(2)
\(X^{*}\) contains a complemented subspace isomorphic to \(L_{1}\);
-
(3)
\(X^{*}\) contains a complemented subspace isomorphic to \(C[0,1]^{*}\);
-
(4)
\(X^{*}\) contains an infinite set K such that K is equivalent to the usual basis of \(\ell _{1}(\Gamma )\) for some \(\Gamma \), [K] is complemented in \(X^{*}\), and K is dense in itself in the weak* topology on \(X^{*}\).
If, in addition, X is separable, then the assertions (1)–(4) are equivalent to
-
(5)
There exists a surjective operator \(T:X\rightarrow C[0,1]\) such that \(T^{*}[C[0,1]^{*}]\) is complemented in \(X^{*}\).
The purpose of this note is to quantify the Hagler–Stegall theorem in the spirit of a large number of recent results on quantitative versions of various theorems on and properties of Banach spaces, such as quantitative versions of Krein’s theorem [6], Gantmacher’s theorem [2], James’ compactness theorem [5], weak sequential completeness and the Schur property [11, 12], the (reciprocal) Dunford–Pettis property [10, 13], the Banach–Saks property [3], etc. More broadly speaking, the present paper contributes to the on-going programme of quantification of Banach space theory.
In the present paper, we quantify the Hagler–Stegall theorem by introducing the following three quantities denoted by lower-case Greek letters and defined as infima of certain sets (when the sets happen to be empty, we use the convention that the corresponding value is \(\infty \)).
Hereinafter X and Y will stand for Banach spaces;  is the space of (bounded, linear) operators from X to Y. We then introduce the following quantities:
is the space of (bounded, linear) operators from X to Y. We then introduce the following quantities:
-
\( \alpha _{Y}(X)= \inf \{{\text {d}}(Y,Z):Z \text { is a subspace of}\) \(X\}\), where \({\text {d}}(Y,Z)\) is the Banach–Mazur distance between Y and Z.
The quantity \(\alpha _{Y}(X)\), being directly related to the Banach–Mazur distance, measures how well Y is from being isomorphically embeddable into X. Obviously, \(\alpha _{Y}(X)=1\) if and only if X contains almost isometric copies of Y, that is, for every \(\varepsilon >0\), X contains a subspace \((1+\varepsilon )\)-isomorphic to Y.
-
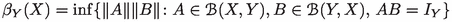 , \(AB=I_{Y}\}\).
, \(AB=I_{Y}\}\).
The quantity \(\beta _{Y}(X)\) measures how well Y is from being isomorphic to a complemented subspace of X. It is easy to see that \(\beta _{Y}(X)=1\) if and only if for every \(\varepsilon >0\), there exists a subspace M of X so that M is \((1+\varepsilon )\)-isomorphic to Y and \((1+\varepsilon )\)-complemented in X.
-
 .
.
The quantity \(\theta _{Y}(X)\) measures how well Y is isomorphic to a quotient of X and its dual \(Y^{*}\) is isomorphic to a complemented subspace of \(X^{*}\). We see that \(\theta _{Y}(X)=1\) if and only if, for every \(\varepsilon >0\), there exists a \((1+\varepsilon )\)-quotient map \(T:X\rightarrow Y\) so that \(T^{*}[Y^{*}]\) is \((1+\varepsilon )\)-complemented in \(X^{*}\).
A straightforward argument shows that
By using the aforementioned three quantities, we quantify the Hagler–Stegall theorem as follows:
Theorem A
Let X be a Banach space. Then
If, in addition, X is separable, then
The following \((1+\varepsilon )\)-version of the Hagler–Stegall theorem follows from Theorem A.
Corollary 1.1
Let X be a Banach space. Then the following assertions are equivalent:
-
(1)
X contains almost isometric copies of \((\bigoplus _{n=1}^{\infty }\ell _{\infty }^{n})_{l_{1}}\);
-
(2)
\(X^{*}\) contains a \((1+\varepsilon )\)-complemented subspace that is \((1+\varepsilon )\)-isomorphic to \(L_{1}\) for every \(\varepsilon >0\);
-
(3)
\(X^{*}\) contains a \((1+\varepsilon )\)-complemented subspace that is \((1+\varepsilon )\)-isomorphic to \(C[0,1]^{*}\) for every \(\varepsilon >0\).
If, in addition, X is separable, then
-
(4)
for every \(\varepsilon >0\), there exists a \((1+\varepsilon )\)-quotient map \(T:X\rightarrow C(\Delta )\) so that \(T^{*}[C(\Delta )^{*}]\) is \((1+\varepsilon )\)-complemented in \(X^{*}\).
2 Preliminaries
Our notation and terminology are standard and mostly in-line with [1, 16]. Throughout the paper, all Banach spaces can be considered either real or complex. We work with real scalars but the results can be easily amended to the complex too. By a subspace we understand a closed, linear subspace and by an operator we understand a bounded, linear map. If X is a Banach space, we denote by \(B_{X}\) the closed unit ball of X, by \(I_{X}\) the identity operator on X, and, for a subset \(K \subseteq X\), by [K] the closed linear span of K. For a surjective operator \(T:X\rightarrow Y\), we set
For \(\lambda \geqslant 1\), we say that a surjective operator \(T:X\rightarrow Y\) is a \(\lambda \)-quotient map if \(\Vert T\Vert {\text {co}}(T)\leqslant \lambda \). Quotient maps are 1-quotient maps according to the above terminology. A norm-one surjective operator \(T:X\rightarrow Y\) is a quotient map if and only if T is a \((1+)\)-quotient map, that is, a \((1+\varepsilon )\)-quotient map for every \(\varepsilon >0\).
The Banach–Mazur distance \({\text {d}}(X,Y)\) between two isomorphic Banach spaces X and Y is defined by \(\inf \Vert T\Vert \Vert T^{-1}\Vert \), where the infimum is taken over all isomorphisms T from X onto Y. As defined by Lindenstrauss and Rosenthal [15], for \(\lambda \geqslant 1\), a Banach space X is said to be a \({\mathcal {L}}_{1,\lambda }\)-space whenever for every finite-dimensional subspace E of X, there is a finite-dimensional subspace F of X such that \(F\supseteq E\) and \({\text {d}}(F,l_{1}^{\dim F})\leqslant \lambda \). We say that a Banach space X is an \({\mathcal {L}}_{1,\lambda +}\)-space if it is an \({\mathcal {L}}_{1,\lambda +\varepsilon }\)-space for all \(\varepsilon >0\).
Following the notation from [8], we denote
and, for \((n,i), (m,j)\in {\mathcal {F}}\), we write \((n,i)\geqslant (m,j)\) whenever
-
\(n\geqslant m\),
-
\(2^{n-m}j\leqslant i\leqslant 2^{n-m}(j+1)-1\).
Let \(\Delta =\{0,1\}^{\mathbb {N}}\) be the Cantor set endowed with the metric
By Miljutin’s theorem [1, Lemma 4.4.7], C[0, 1] is isomorphic (but not isometric) to \(C(\Delta )\). It is well-known that \(C(\Delta )^{*}\) and \(C[0,1]^{*}\) are linearly isometric, though.
3 Proof of Theorem A
The present section is devoted to the proof of Theorem A and is conveniently split into more digestible parts.
Proof of Theorem A
We split the proof into a number of steps.
Step 1. \(\beta _{C(\Delta )^{*}}(X^{*})\leqslant \alpha _{(\bigoplus _{n=1}^{\infty }\ell _{\infty }^{n})_{\ell _1}}(X)\).
Since \(Z = (\bigoplus _{n=1}^{\infty } \ell _{\infty }^{2^{n}})_{\ell _1}\) embeds isometrically into \((\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}\), it suffices to prove that \(\alpha _{Z}(X)\geqslant \beta _{C(\Delta )^{*}}(X^{*})\). For this, let us fix \(c>\alpha _{Z}(X)\). Then there exists a contractive operator \(R:Z\rightarrow X\) that is bounded below by 1/c.
Let us consider a double-indexed family \((\Delta _{n,i})_{n=0, i=0}^{\infty , 2^{n}-1}\) of clopen subsets of the Cantor set such that
-
(1)
\(\Delta _{0,0}=\Delta \), \(\Delta _{n,i}=\Delta _{n+1,2i}\cup \Delta _{n+1,2i+1}\) (\((n,i)\in {\mathcal {F}}\)), and \(\Delta _{n,i}\cap \Delta _{n,j}=\varnothing \) if \(i\ne j\);
-
(2)
the diameter of \(\Delta _{n,i}\) is \(1/{2^{n}}\) (\(0\leqslant i\leqslant 2^{n}-1\)).
We set \(g_{n,i}=\mathbb {1}_{\Delta _{n,i}}\), which is a continuous function, \([g_{n,i}]_{i=0}^{2^{n}-1}\subseteq [g_{n+1,i}]_{i=0}^{2^{n+1}-1}\), \((g_{n,i})_{i=0}^{2^{n}-1}\) is isometrically equivalent to the unit vector basis of \(\ell _{\infty }^{2^{n}}\) (\(n\in {\mathbb {N}}\)), and \(\bigcup _{n=0}^{\infty }[g_{n,i}]_{i=0}^{2^{n}-1}\) is dense in \(C(\Delta )\). We may then define an operator \(T:Z\rightarrow C(\Delta )\) by the assignment \(Te_{n,i}=g_{n,i}\). For each n, T is an isometry when restricted to \([e_{n,i}:0\leqslant i\leqslant 2^{n}-1]\). Clearly, \(\Vert T\Vert =1\).
Claim 1
If W is a finite-dimensional Banach space and \(S:W\rightarrow C(\Delta )\) is an operator, then for every \(\varepsilon >0\), there exists an operator \({\widehat{S}}:W\rightarrow Z\) so that \(\Vert {\widehat{S}}\Vert \leqslant (1+\varepsilon )\Vert S\Vert \) and \(\Vert S-T{\widehat{S}}\Vert \leqslant \varepsilon \).
Proof of Claim 1
Let us fix an Auerbach basis \((w_{k},w_{k}^{*})_{k=1}^{N}\) for W (\(\dim W=N\)). So if \(w=\sum _{k=1}^{N}a_{k}w_{k}\in W\), then for each \(1\leqslant j\leqslant N\), we get
It follows that \(\sum _{k=1}^{N}|a_{k}|\leqslant N\Vert w\Vert .\) Let \(\delta >0\) be such that \(\delta N\leqslant \varepsilon \Vert S\Vert \) and \(\delta N\leqslant \varepsilon \). Then, there exist a positive integer n and \((f_{k})_{k=1}^{N}\) in \([g_{n,i}]_{i=0}^{2^{n}-1}\) so that \(\Vert Sw_{k}-f_{k}\Vert <\delta \) (\(k=1, 2, \ldots , N\)). Let us write \(f_{k}=\sum _{i=0}^{2^{n}-1}t_{k,i}g_{n,i}\) \((k=1, 2, \ldots , N).\)
Let us define an operator \({\widehat{S}}:W\rightarrow Z\) by
We claim that \({\widehat{S}}\) is the required operator. Indeed, for \(w=\sum _{k=1}^{N}a_{k}w_{k}\in W\), we have
Furthermore,
Let \(\varepsilon >0\). Since \(C(\Delta )\) has the metric approximation property (see, e.g., [4] for the definition), there exists a net \((T_{\alpha })_{\alpha }\) of finite-rank operators on \(C(\Delta )\) such that
-
\(\limsup _{\alpha }\Vert T_{\alpha }\Vert \leqslant 1+\varepsilon \),
-
\(\dim T_{\alpha }(C(\Delta ))\rightarrow \infty \),
-
\(T_{\alpha }\rightarrow I_{C(\Delta )}\) strongly.
For each \(\alpha \), we may apply Claim 1 to the inclusion map \(I_{\alpha }:T_{\alpha }[C(\Delta )]\rightarrow C(\Delta )\) in order to get an operator \(\widehat{I_{\alpha }}:T_{\alpha }[C(\Delta )]\rightarrow Z\) such that
-
\(\Vert \widehat{I_{\alpha }}\Vert \leqslant 1+\varepsilon \),
-
\(\Vert I_{\alpha }-T\widehat{I_{\alpha }}\Vert \leqslant (1+\dim T_{\alpha }[C(\Delta )])^{-2}\).
Hence, for \(f\in C(\Delta )\), we get
Let S be a  -cluster point of the net \(((\widehat{I_{\alpha }}T_{\alpha })^{*})_{\alpha }\). We show that \(ST^{*}=I_{C(\Delta )^{*}}\). Indeed, we choose a subnet \(((\widehat{I_{\alpha '}}T_{\alpha '})^{*})_{\alpha '}\) of \(((\widehat{I_{\alpha }}T_{\alpha })^{*})_{\alpha }\) so that \((\widehat{I_{\alpha '}}T_{\alpha '})^{*}\rightarrow S\) in the
-cluster point of the net \(((\widehat{I_{\alpha }}T_{\alpha })^{*})_{\alpha }\). We show that \(ST^{*}=I_{C(\Delta )^{*}}\). Indeed, we choose a subnet \(((\widehat{I_{\alpha '}}T_{\alpha '})^{*})_{\alpha '}\) of \(((\widehat{I_{\alpha }}T_{\alpha })^{*})_{\alpha }\) so that \((\widehat{I_{\alpha '}}T_{\alpha '})^{*}\rightarrow S\) in the  -topology. Then, for \(f\in C(\Delta )\) and \(\mu \in C(\Delta )^{*}\), we get \(\langle (\widehat{I_{\alpha '}}T_{\alpha '})^{*}T^{*}\mu ,f\rangle \rightarrow \langle ST^{*}\mu ,f\rangle \). On the other hand, we have
-topology. Then, for \(f\in C(\Delta )\) and \(\mu \in C(\Delta )^{*}\), we get \(\langle (\widehat{I_{\alpha '}}T_{\alpha '})^{*}T^{*}\mu ,f\rangle \rightarrow \langle ST^{*}\mu ,f\rangle \). On the other hand, we have
Therefore, \(\langle ST^{*}\mu ,f\rangle =\langle \mu ,f\rangle .\)
Claim 2
There exists an operator \({\widetilde{T}}:C(\Delta )^{*}\rightarrow X^{*}\) so that \(R^{*}{\widetilde{T}}=T^{*}\) and \(\Vert {\widetilde{T}}\Vert \leqslant c(1+\varepsilon )\).
The proof of the claim is a variation of the Lindenstrauss’ compactness argument (see [9, Proposition 1] and [14, Lemma 2]). Since certain amendments are required, we present the full reasoning.
Proof of Claim 2
We use the fact that \(C(\Delta )^{*}\) is isometric to \(L_{1}(\mu )\) for some infinite measure \(\mu \), and as such, it is an \({\mathcal {L}}_{1,1+}\)-space. Let \(\Lambda \) be the collection of all finite-dimensional subspaces of \(C(\Delta )^{*}\). Then, for each \(\gamma \in \Lambda \), there exist \(E_{\gamma }\in \Lambda \) with \(\gamma \subseteq E_{\gamma }\) together with an isomorphism \(U_{\gamma }:\ell _{1}^{\dim E_{\gamma }}\rightarrow E_{\gamma }\) so that \(\Vert U_{\gamma }\Vert \Vert U_{\gamma }^{-1}\Vert \leqslant 1+\varepsilon \). Let \(S_{\gamma }:Z\rightarrow E_{\gamma }^{*}\) be an operator such that \(S_{\gamma }^{*}=T^{*}|_{E_{\gamma }}\) (\(\gamma \in \Lambda \)). By the 1-injectivity of \(\ell _{\infty }^{\dim E_{\gamma }}\), there is an operator \(R_{\gamma }:X\rightarrow \ell _{\infty }^{\dim E_{\gamma }}\) so that \(R_{\gamma }R=U_{\gamma }^{*}S_{\gamma }\) and \(\Vert R_{\gamma }\Vert \leqslant \Vert U_{\gamma }^{*}S_{\gamma }\Vert \Vert R^{-1}\Vert \leqslant \Vert U_{\gamma }\Vert \Vert T\Vert \Vert R^{-1}\Vert \). Let \(T_{\gamma }=R_{\gamma }^{*}U_{\gamma }^{-1}:E_{\gamma }\rightarrow X^{*}\). Then \(R^{*}T_{\gamma }= T^{*}|_{E_{\gamma }}\) and \(\Vert T_{\gamma }\Vert \leqslant c(1+\varepsilon )\Vert T\Vert \). For each \(\gamma \), we define a non-linear, discontinuous function from \(C(\Delta )^{*}\) to \(X^{*}\) by
Then \((\widetilde{T_{\gamma }})_{\gamma }\) is a net in the compact space
and as such, it has a cluster point \({\widetilde{T}}\). Standard arguments show that \({\widetilde{T}}\) is linear, \(R^{*}{\widetilde{T}}=T^{*},\) and \(\Vert {\widetilde{T}}\Vert \leqslant c(1+\varepsilon )\Vert T\Vert =c(1+\varepsilon )\).
Finally, we get \(SR^{*}{\widetilde{T}}=ST^{*}=I_{C(\Delta )^{*}}\) and hence
Letting \(\varepsilon \rightarrow 0\), we get \(\beta _{C(\Delta )^{*}}(X^{*})\leqslant c\). As c is arbitrary, we get Step 1.
Step 2. \(\beta _{L_{1}}(X^{*})\leqslant \beta _{C[0,1]^{*}}(X^{*})\).
It is well known that \(L_1\) is isometric to a 1-complemented subspace of \(C[0,1]^{*}\) (see, e.g., [1, p. 85]), which implies Step 2.
Step 3. \(\alpha _{(\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}}(X)\leqslant \beta _{L_{1}}(X^{*})\).
Let \(c>\beta _{L_{1}}(X^{*})\). Then there exist operators \(A:L_{1}\rightarrow X^{*}, B:X^{*}\rightarrow L_{1}\) so that \(BA=I_{L_{1}}, \Vert A\Vert =1\), and \(\Vert B\Vert <c\). Let \(0<\varepsilon <1\) and \(\varepsilon _{n}=\varepsilon /2^{2n+3}\) (\(n=0,1,\ldots \)).
By [8, Lemma 3], we get \((f_{n,i})_{(n,i)\in {\mathcal {F}}}\) in \(L_{\infty }\) and \((x_{n,i})_{(n,i)\in {\mathcal {F}}}\) in X satisfying
-
(1)
\(\Vert f_{n,i}\Vert _{1}=1\) and \(f_{n,i}\geqslant 0\) everywhere for all \((n,i)\in {\mathcal {F}}\);
-
(2)
for each n and \(i\ne j\), \(f_{n,i}(t)\) and \(f_{n,j}(t)\) cannot be both non-zero for the same \(t\in [0,1]\);
-
(3)
$$\begin{aligned}\langle Af_{n,i},x_{m,j}\rangle = \left\{ \begin{array} {rl} 1, &{} (n,i)\geqslant (m,j),\\ 0, &{} \text {otherwise;} \end{array} \right. \end{aligned}$$
-
(4)
\(\max _{0\leqslant i\leqslant 2^{n}-1}|t_{i}|\leqslant \Vert \sum _{i=0}^{2^{n}-1}t_{i}x_{n,i}\Vert \leqslant c(1+\varepsilon _{n}) \max _{0\leqslant i\leqslant 2^{n}-1}|t_{i}|\) (\(n=0,1,\ldots \); \(t_{0},\ldots , t_{2^{n}-1}\in {\mathbb {R}}\)).
We may now define recursively a sequence \((W_{n,i})_{(n,i)\in {\mathcal {F}}}\) of non-empty weak*-closed subsets of \(B_{X^{*}}\) as follows:
-
\(W_{0,0}=\{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{0,0}\rangle -1|\leqslant \varepsilon _{0}\},\)
-
\(W_{1,0}=W_{0,0}\cap \{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{1,0}\rangle -1|\leqslant \varepsilon _{1}, |\langle x^{*},x_{1,1}\rangle |\leqslant \varepsilon _{1}\},\)
-
\(W_{1,1}=W_{0,0}\cap \{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{1,1}\rangle -1|\leqslant \varepsilon _{1}, |\langle x^{*},x_{1,0}\rangle |\leqslant \varepsilon _{1}\},\)
-
\(W_{2,0}=W_{1,0}\cap \{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{2,0}\rangle -1|\leqslant \varepsilon _{2}, |\langle x^{*},x_{2,j}\rangle |\leqslant \varepsilon _{2},j=1,2,3\},\)
-
\(W_{2,1}=W_{1,0}\cap \{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{2,1}\rangle -1|\leqslant \varepsilon _{2}, |\langle x^{*},x_{2,j}\rangle |\leqslant \varepsilon _{2},j=0,2,3\},\)
-
\(W_{2,2}=W_{1,1}\cap \{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{2,2}\rangle -1|\leqslant \varepsilon _{2}, |\langle x^{*},x_{2,j}\rangle |\leqslant \varepsilon _{2},j=0,1,3\},\)
-
\(W_{2,3}=W_{1,1}\cap \{x^{*}\in B_{X^{*}}:|\langle x^{*},x_{2,3}\rangle -1|\leqslant \varepsilon _{2}, |\langle x^{*},x_{2,j}\rangle |\leqslant \varepsilon _{2},j=0,1,2\}\),
and so on. By (3), each \(W_{n,i}\) is non-empty. By the choice of \(\varepsilon _{n}\), the sets \(W_{n,i}, W_{n,j}\) are disjoint as long as \(i\ne j\). Let
By (3), \(Af_{n,i}\in W_{m,j}\) if \((n,i)\geqslant (m,j)\), which implies that each \(K_{n,i}\) is non-empty. By the construction of the sequence \((W_{n,i})\), we see that \(K_{0,0}=K, K_{n+1,2i}\cup K_{n+1,2i+1}=K_{n,i},\) and \(K_{n,i}\cap K_{n,j}=\varnothing \) if \(i\ne j\).
Let us define an operator \(T:X\rightarrow C(K)\) by \(\langle Tx,x^{*}\rangle =\langle x^{*},x\rangle \) (\(x\in X,x^{*}\in K\)). Then \(|\langle Tx_{n,i},x^{*}\rangle -1|\leqslant \varepsilon _{n}\) if \(x^{*}\in K_{n,i}\), and \(|\langle Tx_{n,i},x^{*}\rangle |\leqslant \varepsilon _{n}\) if \(x^{*}\in \bigcup _{j\ne i}K_{n,j}\). Set \(g_{n,i}=\mathbb {1}_{K_{n,i}}\), which is continuous as \(K_{n,i}\) is clopen. Then \(\Vert Tx_{n,i}-g_{n,i}\Vert \leqslant \varepsilon _{n}\). Moreover, \([g_{n,i}]_{i=0}^{2^{n}-1}\subseteq [g_{n+1,i}]_{i=0}^{2^{n+1}-1}\), \((g_{n,i})_{i=0}^{2^{n}-1}\) is isometrically equivalent to the unit vector basis of \(\ell _{\infty }^{2^{n}}\) for all n, and
is isometric to \(C(\Delta )\). Let Z be a subspace of \(C(\Delta )\) isometric to \((\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}\) and let \((z_{n,j})_{n=1,j=0}^{\infty ,n-1}\) be a basis of Z isometrically equivalent to the unit vector basis of \((\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}\). Fix \(n\geqslant 1\). Then there exist \(m>n\) and unit vectors \(h_{n,j}\in [g_{m,i}]_{i=0}^{2^{m}-1}\) so that \(\Vert z_{n,j}-h_{n,j}\Vert \leqslant \varepsilon /2^{n+3}\) (\(j=0,1,\ldots ,n-1\)). We write \(h_{n,j}=\sum _{i=0}^{2^{m}-1}a_{i,j}g_{m,i}\) and define \(y_{n,j}=\sum _{i=0}^{2^{m}-1}a_{i,j}x_{m,i}\in X.\)
Claim 3
For all \((t_{n,j})_{n=1,j=0}^{\infty , n-1}\in (\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}\), we have
Indeed, by (4), we get
Consequently,
On the other hand, by the choice of m and \(h_{n,j}\), we arrive at
This implies that
Finally, by Claim 3, we get
Letting \(\varepsilon \rightarrow 0\) yields \(\alpha _{(\bigoplus _{n=1}^{\infty } \ell _{\infty }^{n})_{\ell _1}}(X)\leqslant c\). Since c was arbitrary, the proof of Step 3 is completed.
Step 4. \(\beta _{L_{1}}(X^{*})\leqslant \theta _{C(\Delta )}(X)\).
This step follows from (1.1) together with Step 2. We are now ready to establish the final step of the proof.
Step 5. Suppose that X is separable. Then \(\theta _{C(\Delta )}(X)\leqslant \beta _{L_{1}}(X^{*})\).
Let \(c>\beta _{L_{1}}(X^{*})\). Then there exist operators \(A:L_{1}\rightarrow X^{*}, B:X^{*}\rightarrow L_{1}\) so that \(BA=I_{L_{1}}, \Vert A\Vert =1\), and \(\Vert B\Vert <c\).
Let \((f_{n,i})_{(n,i)\in {\mathcal {F}}}\) be a family of functions in \(L_{\infty }\), \((x_{n,i})_{(n,i)\in {\mathcal {F}}}\) in X, and \((W_{n,i})_{(n,i)\in {\mathcal {F}}}\) associated to \(\varepsilon _{n}=1/2^{2n+2}\) (\(n=0,1,\ldots \)) as described in Step 3. Since X is separable, we may assume that the \({\text {d}}\)-diameter of \(W_{n,i}\leqslant 2^{-n}\) for each i, where \({\text {d}}\) is a metric giving the relative \(\sigma (X^{*},X)\)-topology on \(B_{X^{*}}\). Let
Then K is a compact, totally disconnected metric space without isolated points, hence homeomorphic to \(\Delta \). Moreover, \(K_{0,0}=K, K_{n+1,2i}\cup K_{n+1,2i+1}=K_{n,i}\), and \(K_{n,i}\cap K_{n,j}=\varnothing \) if \(i\ne j\). Hence \(K=\bigcup _{i=0}^{2^{n}-1}K_{n,i}\) for all n. As seen in Step 3, the operator \(T:X\rightarrow C(K)\), defined by \(\langle Tx,x^{*}\rangle =\langle x^{*},x\rangle \) (\(x\in X,x^{*}\in K\)), satisfies \(\Vert Tx_{n,i}-g_{n,i}\Vert \leqslant \varepsilon _{n}\), where \(g_{n,i}=\mathbb {1}_{K_{n,i}}\in C(K)\).
An argument analogous to Step 1 yields that, if W is a finite-dimensional Banach space and \(S:W\rightarrow C(K)\) is an operator, then, for every \(\varepsilon >0\), there exists an operator \({\widehat{S}}:W\rightarrow X\) so that \(\Vert {\widehat{S}}\Vert \leqslant c(1+\varepsilon )\Vert S\Vert \) and \(\Vert S-T{\widehat{S}}\Vert \leqslant \varepsilon \).
Fix \(\varepsilon >0\). By an argument analogous to the one from Step 1, we get an operator \(S:X^{*}\rightarrow C(K)^{*}\) with \(\Vert S\Vert \leqslant c(1+\varepsilon )^{2}\) so that \(ST^{*}=I_{C(K)^{*}}\). This means that
Letting \(\varepsilon \rightarrow 0\), we arrive at \(\theta _{C(\Delta )}(X)\leqslant c.\) As c is arbitrary, the proof is complete.\(\square \)
References
Albiac, F., Kalton, N.J.: Topics in Banach Space Theory. Springer, Berlin (2005)
Angosto, C., Cascales, B.: Measures of weak non-compactness in Banach spaces. Topol. Appl. 156, 1412–1421 (2009)
Bendová, H., Kalenda, O.F.K., Spurný, J.: Quantification of the Banach-Saks property. J. Funct. Anal. 268, 1733–1754 (2015)
Casazza, P.G.: Approximation properties. In: Johnson, W.B., Lindenstrauss, J. (eds.) Handbook of the Geometry of Banach spaces, vol. 1, pp. 271–316. Elsevier, Amsterdam (2001)
Cascales, B., Kalenda, O.F.K., Spurný, J.: A quantitative version of James’ compactness theorem. Proc. Edinburgh Math. Soc. 55, 369–386 (2012)
Fabian, M., Hájek, P., Montesinos, V., Zizler, V.: A quantitative version of Krein’s theorem. Rev. Mat. Iberoamer. 21, 237–248 (2005)
Hagler, J.: Some more Banach spaces which contain \(l^{1}\). Studia Math. 46, 35–42 (1973)
Hagler, J., Stegall, C.: Banach spaces whose duals contain complemented subspaces isomorphic to \(C[0,1]^{*}\). J. Funct. Anal. 13, 233–251 (1973)
Johnson, W.B.: A complementary universal conjugate Banach space and its relation to the approximation problem. Israel J. Math. 13(3–4), 301–310 (1972)
Kačena, M., Kalenda, O.F.K., Spurný, J.: Quantitative Dunford-Pettis property. Adv. Math. 234, 488–527 (2013)
Kalenda, O.F.K., Pfitzner, H., Spurný, J.: On quantification of weak sequential completeness. J. Funct. Anal. 260, 2986–2996 (2011)
Kalenda, O.F.K., Spurný, J.: On a difference between quantitative weak sequential completeness and the quantitative Schur property. Proc. Amer. Math. Soc. 140, 3435–3444 (2012)
Kalenda, O.F.K., Spurný, J.: Quantification of the reciprocal Dunford-Pettis property. Studia Math. 210, 261–278 (2012)
Lindenstrauss, J.: On nonseparable reflexive Banach spaces. Bull. Amer. Math. Soc. 72, 967–970 (1966)
Lindenstrauss, J., Rosenthal, H.P.: The \({\cal{L} }_{p}\) spaces. Israel J. Math. 7, 325–349 (1969)
Lindenstrauss, J., Tzafriri, L.: Classical Banach Spaces. I. Sequence Spaces.Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 92. Springer, Berlin-New York (1977)
Pełczyński, A.: On Banach spaces containing \(L_{1}(\mu )\). Studia Math. 30, 231–246 (1968)
Acknowledgements
The authors would like to thank Prof. W.B. Johnson for helpful discussions and comments. The first-named author was supported by the National Natural Science Foundation of China (Grant No.11971403) and the Natural Science Foundation of Fujian Province of China (Grant No. 2019J01024). The second-named author acknowledges with thanks funding received from NCN SONATA 15 grant No. 2019/35/D/ST1/01734.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, D., Kania, T. & Ruan, Y. \((1+)\)-complemented, \((1+)\)-isomorphic copies of \(L_{1}\) in dual Banach spaces. Arch. Math. 119, 495–505 (2022). https://doi.org/10.1007/s00013-022-01778-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-022-01778-2




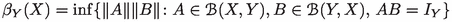 ,
,  .
.