Abstract
This article presents an extension of Lewis’ analysis of counterfactuals to a graded framework. Unlike standard graded approaches, which use the probabilistic framework, we employ that of many-valued logics. Our principal goal is to provide an adequate analysis of the main background notion of Lewis’ approach—the one of the similarity of possible worlds. We discuss the requirements imposed on the analysis of counterfactuals by the imprecise character of similarity and concentrate in particular on robustness, i.e., the requirement that small changes in the similarity relation should not significantly change the truth value of the counterfactual in question. Our second motivation is related to the logical analysis of natural language: analyzing counterfactuals in the framework of many-valued logics allows us to extend the analysis to counterfactuals that include vague statements. Unlike previous proposals of this kind in the literature, our approach makes it possible to apply gradedness at various levels of the analysis and hence provide a more detailed account of the phenomenon of vagueness in the context of counterfactuals. Finally, our framework admits a novel way of avoiding the Limit Assumption, keeping the core of Lewis’ truth condition for counterfactuals unchanged.




Similar content being viewed by others
Notes
Lewis regarded counterfactuals as manifesting both imprecision and vagueness. The following quote from Lewis speaks of the vagueness of counterfactuals; regarding their imprecision, see his quote at the beginning of Sect. 3 (p. 6).
Stalnaker’s semantics based on selection functions (1968, Sect. 2) makes an even stronger assumption, namely, that there is always the unique closest possible world. Lewis’ system with the LA can be recast in terms of a set selection function, i.e., a function returning the set of closest possible worlds instead of a single one.
We use the common convention (cf., e.g., Lewis 1973a) of referring to the worlds satisfying the antecedent A of a counterfactual
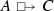 as A-worlds. Analogously, we refer to the worlds satisfying both the antecedent and the consequent as AC-worlds, and to the worlds satisfying the antecedent but not the consequent as \(A{\lnot }C\)-worlds.
as A-worlds. Analogously, we refer to the worlds satisfying both the antecedent and the consequent as AC-worlds, and to the worlds satisfying the antecedent but not the consequent as \(A{\lnot }C\)-worlds.Although traditionally called similarity orderings (e.g., Lewis 1973a), the relations \(\le _w\) are generally just preorders since antisymmetry is not required.
We formulate the definitions in such a way that they can easily be generalized to the many-valued semantics introduced later in this paper. Clearly, in the bivalent semantics, the intension \({\left\| {A}\right\| ^{M}_{}}\) can be identified with the set of A-worlds, i.e., with the set \(\{ {w\in W} \mid {\left\| {A}\right\| ^{M}_{w}}=1 \}\).
These perturbations may be due, e.g., to minor shifts in the importance of particular respects of comparison posited by Lewis (1973a, p. 91): “Overall similarity consists of innumerable similarities and differences in innumerable respects of comparison, balanced against each other according to the relative importances we attach to those respects of comparison. Insofar as these relative importances differ from one person to another or differ from one occasion to another or are indeterminate even for a single person on a single occasion, so far is comparative similarity indeterminate.”
To avoid sorites arguments based on accumulating small changes in similarity or valuation, robustness needs to be restricted to non-borderline cases (or the meaning of “small change” be made more precise) in bivalent frameworks. In many-valued frameworks, however, robustness can be ensured if small perturbations only produce small changes in truth degrees.
As pointed out by an anonymous reviewer, non-robustness can be considered a desirable feature of counterfactuals since they can be explicated in terms of necessity (“a variably strict conditional”, e.g., Lewis 1973a, p. 13), and thus as involving universal quantification over possible worlds. Our emphasis is on the variability and vagueness of the necessity spheres, and thus of the domain of the universal quantification, where a small change in the similarity relation may affect which worlds are counted among the closest A-worlds. Thus, indeed, a single central counterexample (i.e., a single \({\lnot }C\)-world among the robustly-closest A-worlds) can be regarded as falsifying the counterfactual. Nevertheless, tolerance to exceptions in the fragile borders of the variable quantification domain can still be seen as desirable.
Note, however, that robustness is not the only criterion by which Leitgeb’s and Bennett’s approaches should be compared to Lewis’ system. They can rather be viewed as providing a fairly different analysis of counterfactual conditionals, reaching opposite conclusions about the validity of certain logical rules (e.g., conjunction in the consequent).
It also differs from Leitgeb’s, who says (2012, p. 28): “In all of this, our chief interest will be in counterfactuals that are true or false in virtue of causal matters rather than, for example, by linguistic convention.”
To avoid awkward notation, further on we write just \(\left\| {\psi (w)}\right\| ^{M'}\) instead of the more correct \(\left\| {\psi (x)}\right\| ^{M'}_{x\mapsto w}\). Since the language of the formula disambiguates which model is used, we may omit the superscripts \(M,M'\) too. Moreover, if the context clearly indicates that the truth value of \(\psi \) is meant, we may write just \(\psi \) for \(\left\| {\psi }\right\| \).
We denote graded predicates in boldface.
As an alternative, they provide a solution parameterized by the degree of truth of A.
This analysis can be rephrased within the framework of fuzzy modal logics (e.g., Hájek 1998, sect. 8.3; Hájek 2010; Běhounek and Majer 2018), using Lewis’ interpretation of a counterfactual as a “variably strict conditional” \(\Box _A ({A\rightarrow C})\), where the modality \(\Box _A\) means necessity that is restricted to the A-minimal similarity sphere.
Fuzzy indistinguishability relations are also called similarity relations or fuzzy equivalence relations in the literature.
Although in many particular models they are. Note that Lewis (1973a, p. 51) did not find the restriction to numeric distances too limiting.
Thus, they are not subject to Lewis’ criticism of metric distances (1973a, p. 51).
Note that due to the existence of non-standard algebras for Łukasiewicz logic (see Appendix 1), even the degrees of closeness need not be numeric, but can be abstract.
Note that the abstract distances in a distance-based counterfactual frame are just a mathematical tool employed for technical reasons, which has no semantic consequences beyond the world-similarity ordering \(\preccurlyeq _w\) it generates (by Definition 7 below). Consequently, the existence of uninhabited spheres in the model has no bearing on which possible worlds can exist or how many possible worlds there are. In fact, no matter how many and which worlds exist in the model, it is always possible to add artificial distance points between them (with a suitably defined indistinguishability relation), and thereby create uninhabited spheres. Thus, in particular, the existence of uninhabited spheres does not preclude Lewis’ conception of the plenitude of worlds (1986, Sect. 1.8), as the uninhabited abstract distances can always be added ex post, after the frame accounts for all the worlds in existence.
Separation (i.e., the left-to-right direction in the separating reflexivity condition) ensures that the fuzzy ordering
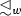 on distances (as defined below) is antisymmetric.
on distances (as defined below) is antisymmetric.If \(\unlhd _w\) is identified with its characteristic function, the definition can equivalently be written as
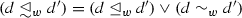 , where \(\mathbin {\vee }\) is the lattice disjunction of Łukasiewicz logic (i.e., the maximum; see Appendix 1). The construction is well-known from the theory of fuzzy orderings (e.g., Bodenhofer 2003, Sect. 7).
, where \(\mathbin {\vee }\) is the lattice disjunction of Łukasiewicz logic (i.e., the maximum; see Appendix 1). The construction is well-known from the theory of fuzzy orderings (e.g., Bodenhofer 2003, Sect. 7).Assuming the (countable) Axiom of Choice, the condition just precludes the full distinguishability of all elements in an infinite decreasing sequence of distances.
Robustness regarding exceptions is also related to the problem discussed in the literature under the name of counterfactual scepticism. (We thank an anonymous reviewer for pointing out this connection to us.) In most of its forms, counterfactual scepticism contends that all or many counterfactuals are false (e.g., Hájek 2020), one of the reasons being events that are rare (exceptional, highly improbable, etc.) but that can still occur in worlds very similar to ours. There are a number of solutions to this problem proposed in the literature (e.g., Lewis 2016; Sandgren and Steele 2020). The discussion of how the robust version of the graded semantic could help resolve the objections raised by counterfactual scepticism is, however, beyond the scope of this paper and left for future research.
The conditions in Definitions 5 and 7 are clearly expressible by formulae in first-order Łukasiewicz logic. The condition of right-connectedness (Definition 8) is second-order, as it refers to sets of distances. Nevertheless, Theorem 1 only needs the condition to hold for sets derived from the intensions of
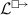 -formulae, and so it can be replaced by a schema of first-order formulae in Łukasiewicz logic and still guarantee the dispensability of the LA.
-formulae, and so it can be replaced by a schema of first-order formulae in Łukasiewicz logic and still guarantee the dispensability of the LA.Propositional Łukasiewicz logic with \({\triangle }\) is denoted by \({\mathrm L}_{\triangle }\). Our ground logic throughout this paper is \({\mathrm L}_{\triangle }\) rather than just \({\mathrm L}\).
General \({\mathrm {MV}_{\triangle }}\)-algebras (unlike \([0,1]_{{\mathrm L}_{\triangle }}\), which is lattice-complete) need not possess all the suprema and infima required for the interpretation of the quantifiers. Consequently, only safe models, i.e., those in which the values of all formulae are well-defined, are considered for non-standard semantics.
Note that the theorem assumes a stronger variant of right-connectivity (Běhounek 2016, Def. 2.16); the assumption is satisfied in our setting since \(({d_0\sim _w d'})>0\) for some \({d'\rhd _wd_0}\), as required by the stronger definition. The remaining assumptions of the theorem are ensured by the fact that \(\unlhd _w\) is a linear lattice-complete order and \(\sim _w\) is a graded indistinguishability relation compatible with \(\unlhd _w\).
References
Adams, E.W. (1975). The Logic of Conditionals: An Application of Probability to Deductive Logic. Springer
Běhounek, L. (2014a). Fuzzified linear orderings, fuzzy maxima and minima. Tech. Rep. V-1195, Institute of Computer Science, Academy of Sciences of the Czech Republic, Prague, available at http://hdl.handle.net/11104/0233644
Běhounek, L. (2014b). In which sense is fuzzy logic a logic for vagueness? In: Łukasiewicz T, Peñaloza R, Turhan AY (eds) Logics for Reasoning about Preferences, Uncertainty, and Vagueness (PRUV 2014). CEUR Workshop Proceedings, Vol-1205, pp 26–38
Běhounek, L. (2016). Maxima and minima in fuzzified linear orderings. Fuzzy Sets and Systems, 289, 82–93.
Běhounek, L., & Majer, O. (2018). Fuzzy intensional semantics. Journal of Applied Non-Classical Logics, 28, 348–388.
Běhounek, L., Cintula, P., Hájek, P. (2011). Introduction to mathematical fuzzy logic. In: Cintula P, Hájek P, Noguera C (eds) Handbook of Mathematical Fuzzy Logic, vol I, College Publications, chap 1, pp. 1–101
Bennett, J. (2003). A Philosophical Guide to Conditionals. Cambridge: Oxford University Press.
Bodenhofer, U. (2000). A similarity-based generalization of fuzzy orderings preserving the classical axioms. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 8(5), 593–610.
Bodenhofer, U. (2003). Representations and constructions of similarity-based fuzzy orderings. Fuzzy Sets and Systems, 137, 113–136.
Bodenhofer, U., De Baets, B., & Fodor, J. (2007). A compendium of fuzzy weak orders: Representations and constructions. Fuzzy Sets and Systems, 158, 811–829.
Cerami, M., Pardo, P. (2011). Many-valued semantics for vague counterfactuals. In: Cintula P, Fermüller CG, Godo L, Hájek P (eds) Understanding Vagueness—Logical, Philosophical, and Linguistic Perspectives, College Publications, pp. 341–362
Chagrov, A., & Zakharyaschev, M. (1997). Modal logic. Cambridge: Oxford University Press.
Cignoli, R., D’Ottaviano, I. M. L., & Mundici, D. (1999). Algebraic foundations of many-valued reasoning. Dordercht: Kluwer.
Delgado, M., Ruiz, M. D., Sánchez, D., & Vila, M. A. (2014). Fuzzy quantification: A state of the art. Fuzzy Sets and Systems, 242, 1–30.
DiNola, A., Leuştean, I. (2011). Łukasiewicz logic and MV-algebras. In: Cintula P, Hájek P, Noguera C (eds) Handbook of Mathematical Fuzzy Logic, vol 2, College Publications, chap 6, pp. 469–583
Dvořák, A., & Holčapek, M. (2014). Type \(\langle 1,1\rangle \) fuzzy quantifiers determined by fuzzy measures on residuated lattices. Part I. Basic definitions and examples. Fuzzy Sets and Systems, 242, 31–55.
Hájek, A. (2020). Counterfactual scepticism and antecedent-contextualism. Synthese (forthcoming). https://doi.org/10.1007/s11229-020-02686-0.
Hájek, P. (1998). Metamathematics of Fuzzy Logic. Dordrecht: Kluwer.
Hájek, P. (2010). On fuzzy modal logics S5(\(\cal{C}\)). Fuzzy Sets and Systems, 161, 2389–2396.
Jackson, F. (1987). Conditionals. Oxford: Blackwell.
Leitgeb, H. (2012). A probabilistic semantics for counterfactuals. Part A. The Review of Symbolic Logic, 5(1), 26–84.
Lewis, D. (1973a). Counterfactuals. Oxford: Blackwell.
Lewis, D. (1973b). Counterfactuals and comparative possibility. Journal of Philosophical Logic, 2, 418–446.
Lewis, D. (1986). On the Plurality of Worlds. Oxford: Blackwell.
Lewis, K. S. (2016). Elusive counterfactuals. Noûs, 50(2), 286–313.
Novák, V. (2008). A formal theory of intermediate quantifiers. Fuzzy Sets and Systems, 159, 1229–1246.
Recasens, J. (2011). Indistinguishability Operators: Modelling Fuzzy Equalities and Fuzzy Equivalence Relations. Berlin, Heidelberg: Springer.
Sandgren, A., & Steele, K. (2020). Levelling counterfactual scepticism. Synthese (forthcoming). https://doi.org/10.1007/s11229-020-02742-9.
Smith, N. J. J. (2008). Vagueness and Degrees of Truth. Cambridge: Oxford University Press.
Stalnaker, R. C. (1968). A theory of conditionals. In Rescher N (Ed.), Studies in Logical Theory (pp. 98–112). Oxford: Blackwell.
Valverde, L. (1985). On the structure of \(F\)-indistinguishability operators. Fuzzy Sets and Systems, 17(3), 313–328.
Acknowledgements
L. Běhounek’s work was supported by the project LQ1602 in the program NPU II of the Ministry of Education, Youth and Sports of the Czech Republic. O. Majer’s work was supported by the grant GA18–00113S of the Czech Science Foundation. We thank an anonymous reviewer for suggestions that helped improve the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
1 The many-valued logic of Łukasiewicz
Fuzzy logics form an intensively studied and well-understood family of many-valued logics, designed especially for handling gradable (i.e., capable of being more or less true) propositions. For an introduction to formal fuzzy logic see, e.g., Hájek (1998) or Běhounek et al. (2011). In this paper, we restrict our attention to Łukasiewicz fuzzy logic (e.g., Hájek 1998; Cignoli et al. 1999; DiNola and Leuştean 2011).
The standard semantics of infinite-valued Łukasiewicz logic (\({\mathrm L}\)) evaluates formulae in the real unit interval [0, 1]. The truth value 1 is usually understood as the full truth of the proposition; the truth value 0 as the full falsity; and the intermediate truth values as the degrees of (partial) truth of gradable propositions. Łukasiewicz logic, thus, generalizes the Boolean logic of bivalent (or, in the terminology of fuzzy logic, crisp) propositions by admitting a gradual change between the truth and falsity of the propositions. The propositional connectives of \({\mathrm L}\) are interpreted truth-functionally, with the following truth functions on [0, 1]:
This entails, in particular, the following values of implication:
Notice that Łukasiewicz logic possesses two conjunctive connectives: the lattice conjunction \(\wedge \), interpreted as the minimum, and the residuated conjunction \( \mathbin { \& }\), which is non-idempotent: \( {x\mathbin { \& }x}<x\) if \(0<x<1\). We will also need the following connective, which (in the standard semantics) crisply asserts the full truth of its argument:Footnote 28
To save some parentheses, we will assume that the unary connectives \({\lnot },{\triangle }\) have the largest and \({\mathrel {\rightarrow }},{\mathrel {\leftrightarrow }}\) the smallest priority in formulae.
The tautologies of propositional Łukasiewicz logic are the formulae that evaluate to 1 under all [0, 1]-evaluations of propositional letters. The set of propositional tautologies of Łukasiewicz logic can be axiomatized, e.g., by the following Hilbert-style axiomatic system for the primitive connectives \(\mathrel {\rightarrow },{\lnot },{\triangle }\):Footnote 29
The derivation rules are modus ponens (from \(\varphi \) and \(\varphi \mathrel {\rightarrow }\psi \) derive \(\psi \)) and \({\triangle }\)-necessitation (from \(\varphi \) derive \({\triangle }\varphi \)). The remaining connectives are defined as follows:
The aforementioned axiomatic system is sound and complete w.r.t. the standard [0, 1]-semantics of \({\mathrm L}_{\triangle }\): a formula is provable iff it is a tautology of \({{\mathrm L}_{\triangle }}\). It should be noted that the standard [0, 1]-valued semantics is not the only sound and complete algebraic semantics for Łukasiewicz logic. The algebras for which \({{\mathrm L}_{\triangle }}\) is sound are called \({\mathrm {MV}_{\triangle }}\)-algebras (see, e.g., Hájek 1998, Sects. 2.4, 3.2; Běhounek et al. 2011, Sects. 1.3, 2.2.1). The logic \({{\mathrm L}_{\triangle }}\) is also sound and complete w.r.t. the class of all \({\mathrm {MV}_{\triangle }}\)-algebras, as well as w.r.t. the class of all linearly ordered \({\mathrm {MV}_{\triangle }}\)-algebras (where the ordering is determined by the lattice connectives \(\mathbin {\vee },\mathbin {\wedge }\)). The interval [0, 1] equipped with the aforementioned truth functions of connectives is called the standard \({\mathrm {MV}_{\triangle }}\)-algebra and denoted by \([0,1]_{{{\mathrm L}_{\triangle }}}\); other \({\mathrm {MV}_{\triangle }}\)-algebras are called non-standard. Non-standard \({\mathrm {MV}_{\triangle }}\)-algebras provide algebraic semantics for Łukasiewicz logic in which the degrees can have abstract, non-numerical values.
First-order Łukasiewicz logic \({{\mathrm L}\forall _{\triangle }}\) extends the propositional syntax in the usual way. Semantically, in a model for a given first-order language \(\mathcal L\) over an \({\mathrm {MV}_{\triangle }}\)-algebra L (standardly, \(L=[0,1]_{{\mathrm L}_{\triangle }}\)) and the domain of discourse U, the n-ary predicate symbols of \(\mathcal L\) are interpreted as functions \(U^n\rightarrow L\), assigning degrees from L to each n-tuple of objects from U. The n-ary function symbols of \(\mathcal L\) are interpreted as in classical logic, by functions \(U^n\rightarrow U\). The truth value of a formula \(\varphi \) in a model M under an evaluation e of individual variables will be denoted by \(\left\| {\varphi }\right\| _e^M\). The interpretation of the quantifiers \(\forall \) and \(\exists \) is, respectively, that of the infimum and the supremum of the truth values of all instances of the quantified formula:
where \(e[x\mapsto a]\) assigns a to x and otherwise coincides with e.
Unlike propositional Łukasiewicz logic, the standard [0, 1]-semantics of its first-order variant is not axiomatizable without infinitary rules. Nevertheless, its general and linear semantics, i.e., the logic of safeFootnote 30 models over all (linearly ordered) \({\mathrm {MV}_{\triangle }}\)-algebras, can be axiomatized by extending the propositional axiomatic system by the derivation rule of generalization (from \(\varphi \) derive \((\forall {x})\varphi \)) and the following axioms for quantifiers:
where t is a term substitutable for x in \(\varphi \) and \(\psi \) does not contain free x. The existential quantifier is defined in Łukasiewicz logic by \((\exists {x})\varphi \equiv {\lnot }(\forall {x}){\lnot }\varphi \). For more details on first-order Łukasiewicz logic see, e.g., Hájek (1998, Sect. 5.4); Běhounek et al. (2011, Sect. 5.1).
2 Proofs
In this appendix, we collect the proofs of the claims from the main text.
Corollary 2 (p. 18) In every fuzzy counterfactual frame, the fuzzy relations \({\preccurlyeq _w},{\approx _w}\) satisfy the following properties, for all \(w,u,v,v',{v''\in W}\):
-
1.
Reflexivity and symmetry: \(({u\preccurlyeq _wu})=({u\approx _wu})=1\) and \(({u\approx _wv})=({v\approx _wu})\).
-
2.
Congruence: If \({v\equiv _wv'}\), then \(({u\preccurlyeq _wv})=({u\preccurlyeq _wv'})\) as well as \(({v\preccurlyeq _wu})=({v'\preccurlyeq _wu})\).
-
3.
Compatibility with \(\le _w\):
If \(v\le _w{v'\le _wv''}\), then \(({v\approx _wv''})\le ({v\approx _wv'})\) and \(({v\approx _wv''})\le ({v'\approx _wv''})\).
Proof
-
1.
Reflexivity and symmetry are immediate by the linearity of \(\preccurlyeq _w\) and the definition of \(\approx _w\).
-
2.
By assumption, \(({v\preccurlyeq _wv'})=({v'\preccurlyeq _wv})=1\). Thus, \( ({u\preccurlyeq _wv})=({u\preccurlyeq _wv})\mathbin { \& }1=({u\preccurlyeq _wv})\mathbin { \& }({v\preccurlyeq _wv'})\le ({u\preccurlyeq _wv'})\) by transitivity; and analogously for the converse.
-
3.
By assumption, \(({v\preccurlyeq _wv'})=({v'\preccurlyeq _wv''})=({v\preccurlyeq _wv''})=1\). Consequently, \( ({v\approx _wv''})=({v''\preccurlyeq _wv})=({v'\preccurlyeq _wv''})\mathbin { \& }({v''\preccurlyeq _wv})\le ({v'\preccurlyeq _wv})=({v\approx _wv'})\); the second claim is proved analogously.
\(\square \)
Proposition 1 (p. 20) Let \(F=(W,\{ {\le _w} \}_{w\in W})\) be a counterfactual frame of Definition 1. Then there is a distance-based counterfactual frame \(\Phi \) on W such that its similarity orderings \(\le _w\) coincide with those of F.
Proof
Let \(D_w=W/{\equiv _w}\) for every \(w\in W\), i.e., \(D_w=\{ [u]_{\equiv _w} \mid {u\in W} \}\), where \([u]_{\equiv _w}\) are the equivalence classes \( [u]_{\equiv _w}=\{ {v\in W} \mid ({v\le _wu})\mathbin { \& }({u\le _wv)} \}\). Set \([u]_{\equiv _w}\unlhd _w[v]_{\equiv _w}\) iff \({u\le _wv}\), for all \({u,v\in W}\) (Corollary 2.2 ensures that \(\unlhd _w\) is well-defined), and let \(\delta _w(u)=[u]_{\equiv _w}\) for all \({u\in W}\). Then \(\Phi \) obviously satisfies the conditions of Definition 6 and by definition, \(u\le _wv\) iff \([u]_{\equiv _w}\unlhd _w[v]_{\equiv _w}\) iff \(\delta _w(u)\unlhd _w\delta _w(v)\). \(\square \)
Proposition 2 (p. 22) Let \(\Phi \) be a distance-based fuzzy counterfactual frame of Definition 7. Then \(\bigl (W,\{ {\preccurlyeq _w} \}_{w\in W}\bigr )\) is a fuzzy counterfactual frame in the sense of Definition 5, where \(\preccurlyeq _w\) are the graded orderings of worlds in \(\Phi \) as defined in Definition 7.
Proof
Fuzzy transitivity and linearity of \(\preccurlyeq _w\) follow directly from the corresponding properties of Corollary 3. The strict minimality of w in \(\preccurlyeq _w\) is proved as follows, using Corollary 3.5 and the properties of the distance \(0_w\) ensured by Definition 6: \(({v\preccurlyeq _ww})=1\) iff  iff \({\delta _w(v)\unlhd _w\delta _w(w)}\) iff \({\delta _w(v)\unlhd _w0_w}\) iff \({\delta _w(v)=0_w}\) iff \({v=w}\). \(\square \)
iff \({\delta _w(v)\unlhd _w\delta _w(w)}\) iff \({\delta _w(v)\unlhd _w0_w}\) iff \({\delta _w(v)=0_w}\) iff \({v=w}\). \(\square \)
Proposition 3 (p. 22) Let \(F=\bigl (W,\{ {\preccurlyeq _w} \}_{w\in W}\bigr )\) be a fuzzy counterfactual frame of Definition 5. Then there is a distance-based fuzzy counterfactual frame \(\Phi \) on W such that its graded similarity orderings \(\preccurlyeq _w\) coincide with those of F.
Proof
For each \(w\in W\), define \(D_w,\unlhd _w,\delta _w\) as in the proof of Proposition 1, and furthermore set \(\bigl ([u]_{\equiv _w}\sim _w[v]_{\equiv _w}\bigr )=(u\approx _wv)\) for all \(u,v\in W\). (By Corollary 2.2, \(\equiv _w\) is a congruence w.r.t. \(\approx _w\), so \(\sim _w\) is well-defined.) The properties of \(\sim _w\) required by Definition 7 then follow straightforwardly from the corresponding properties of \(\approx _w\). Moreover,  . \(\square \)
. \(\square \)
Theorem 1 (p. 23) Let \(\Phi \) be a right-connected distance-based fuzzy counterfactual frame as in Definition 7. Let M be a model over \(\Phi \) and \(M'\) the corresponding first-order model as in Section 4.3.
If \(\left\| {\varvec{A}(v)}\right\| ^{M'}>0\) for some \({v\in W}\), then \(\left\| {({ Min}_{\preccurlyeq _w}\varvec{A})(v^*)}\right\| ^{M'}>0\) for some \({v^*\in W}\).
The proof of Theorem 1 is based on a lemma known from the theory of linear fuzzy orderings, which asserts that under certain conditions, the fuzzy minima of all non-empty fuzzy sets are non-empty (Běhounek 2016, Sect. 3). Here we adapt the lemma for the setting of right-connected distance-based fuzzy counterfactual frames:
Lemma 1
Let \(\Phi \) be a right-connected distance-based fuzzy counterfactual frame as in Definition 7 and \(w\in W\). For any \(\varvec{D}:D_w\rightarrow [0,1]\), define  analogously to (8), i.e., by setting for all \(d\in D_w\):
analogously to (8), i.e., by setting for all \(d\in D_w\):

where \(\mathrel {\rightarrow }\) is the truth function of Łukasiewicz implication (see Appendix 1).
If \(\varvec{D}(d)>0\) for some \(d\in D_w\), then  for some \(d^*\in D_w\).
for some \(d^*\in D_w\).
Proof
Suppose that \(\varvec{D}(d)>0\) for some \(d\in D_w\). Let \(D^+=\{ d'\in D_w \mid \varvec{D}(d')>0 \}\) and \(d_0=\inf _{\unlhd _w}D^+\). If \(\varvec{D}(d_0)>0\), then it is easy to verify by (9) that  .
.
Assume that \(\varvec{D}(d_0)=0\). Since \(\sim _w\) is right-connected in \(d_0=\inf _{\unlhd _w}D^+\), there is \(d'\in D^+\) such that \(({d'\sim _wd_0})>0\). Moreover, \(d'\rhd _wd_0\), since \(d_0=\inf _{\unlhd _w}D^+\notin D^+\) and \(d'\in D^+\). The existence of \(d^*\) such that  then follows by a known theorem on fuzzy orders (Běhounek 2016, Th. 3.2).Footnote 31\(\square \)
then follows by a known theorem on fuzzy orders (Běhounek 2016, Th. 3.2).Footnote 31\(\square \)
Proof of Theorem 1
Set \(\varvec{D}_A(d)=\sup \{ \varvec{A}(u) \mid {u\in W},\ \delta _w(u)>0 \}\) for all \({d\in D_w}\). By assumption, \(\varvec{A}(v)>0\) for some \(v\in W\); thus also \(\varvec{D}_A(d)>0\) for some \(d\in D_w\) (namely, for \(d=\delta _w(v)\)). Consequently, by Lemma 1, there exists \(d^*\in D_w\) such that  .
.
By (9),  ; thus,
; thus,  , which by the definition of \(\varvec{D}_A\) implies that \(d^*=\delta _w(v^*)\) for some \(v^*\in W\). Let us show that \(({ Min}_{\preccurlyeq _w}\varvec{A})(v^*)>0\):
, which by the definition of \(\varvec{D}_A\) implies that \(d^*=\delta _w(v^*)\) for some \(v^*\in W\). Let us show that \(({ Min}_{\preccurlyeq _w}\varvec{A})(v^*)>0\):
For any \(v'\in W\), we have that \(\varvec{A}(v')\le \varvec{D}_A\bigl (\delta _w(v')\bigr )\) by the definition of \(\varvec{D}_A\) and that  by Definition 7. Thus, by the antitonicity of Łukasiewicz implication in the first argument (see Appendix 1),
by Definition 7. Thus, by the antitonicity of Łukasiewicz implication in the first argument (see Appendix 1),

whence

\(\square \)
Rights and permissions
About this article
Cite this article
Běhounek, L., Majer, O. A graded semantics for counterfactuals. Synthese 199, 11963–11994 (2021). https://doi.org/10.1007/s11229-021-03320-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-021-03320-3



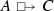 as A-worlds. Analogously, we refer to the worlds satisfying both the antecedent and the consequent as AC-worlds, and to the worlds satisfying the antecedent but not the consequent as
as A-worlds. Analogously, we refer to the worlds satisfying both the antecedent and the consequent as AC-worlds, and to the worlds satisfying the antecedent but not the consequent as 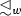 on distances (as defined below) is antisymmetric.
on distances (as defined below) is antisymmetric.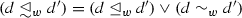 , where
, where 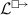 -formulae, and so it can be replaced by a schema of first-order formulae in Łukasiewicz logic and still guarantee the dispensability of the LA.
-formulae, and so it can be replaced by a schema of first-order formulae in Łukasiewicz logic and still guarantee the dispensability of the LA.