Evolution of Aggression in Consumer-Resource Models

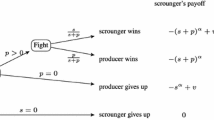
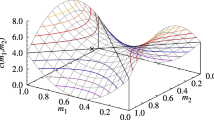
Abstract

The Hawk–Dove model has been used to explain how aggression evolves in animal species. However, testing this model with experimental data has proven challenging because the two model parameters, V and C, are difficult to measure. We propose a novel consumer-resource model that overcomes these difficulties, and we explore the dynamical behavior of the model. Furthermore, by studying a series of consumer-resource models with interactions based on the Hawk–Dove game, we make new predictions for how the level of aggression may change with the richness of the environment, animal mortality, and the amount of time spent fighting.

A Model (6) analysis

First, we reparametrize model (6). This reparametrization is important in stability analysis given below because it allows us to derive in Mathematica conditions for local equilibria stability analytically. This is not possible for the original parametrization of the model given in the article.

Let $R = \alpha \tilde{R},\,N=\gamma \tilde{N}, t = \delta \tau$. Then,

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}\tilde{R}}{\textrm{d}\tau }&= \delta \left[ r\tilde{R}\left( 1-\frac{\alpha }{K}\tilde{R}\right) -\lambda \gamma \tilde{R} \tilde{N}\right] \\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{\delta }{2} (e \lambda \alpha \tilde{R}-C p)(1-p)p\\ \frac{\textrm{d}\tilde{N}}{\textrm{d}\tau }&=\frac{\delta }{2}(e \lambda \alpha \tilde{R}-C p^2-2 m)\tilde{N}. \end{aligned} \end{aligned}$$

(8)

Letting $\delta = \frac{1}{C},\,\gamma =\frac{C}{\lambda },$ and $\alpha = \frac{C}{e\lambda }$, we obtain after simplification,

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}\tilde{R}}{\textrm{d}\tau }&= \frac{r}{C}\tilde{R}\left( 1-\frac{C}{e \lambda K}\tilde{R}\right) - \tilde{R} \tilde{N}\\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{1}{2} (\tilde{R}- p)(1-p)p\\ \frac{\textrm{d}\tilde{N}}{\textrm{d}\tau }&=\frac{1}{2}\left( \tilde{R}- p^2-\frac{2}{C} m\right) \tilde{N}. \end{aligned} \end{aligned}$$

(9)

Now we reparametrize with $\tilde{r} = \frac{r}{C},\,\tilde{K} = \frac{e\lambda K}{C},\,\tilde{m}=\frac{2}{C} m$ to yield

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}\tilde{R}}{\textrm{d}\tau }&= \tilde{r}\tilde{R}\left( 1-\frac{\tilde{R}}{\tilde{K}}\right) - \tilde{R} \tilde{N}\\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{1}{2} (\tilde{R}- p)(1-p)p\\ \frac{\textrm{d}\tilde{N}}{\textrm{d}\tau }&=\frac{1}{2}(\tilde{R}- p^2-\tilde{m})\tilde{N}. \end{aligned} \end{aligned}$$

(10)

Finally, we can drop the tildes to obtain the system

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}R}{\textrm{d}\tau }&= rR\left( 1-\frac{R}{K}\right) - R N\\ \frac{\textrm{d}p}{\textrm{d}\tau }&=\frac{1}{2} (R- p)(1-p)p\\ \frac{\textrm{d}N}{\textrm{d}\tau }&=\frac{1}{2}(R- p^2-m)N. \end{aligned} \end{aligned}$$

(11)

The new state variables correspond to the old ones by $\tilde{R} = \frac{e \lambda }{C}R,\,\tilde{N} = \frac{\lambda }{C}N$.

The advantage of model reparametrization is that model (11) can be analyzed using Mathematica. First, we calculated equilibria and then, using the Routh-Hurwitz criterion we derived conditions for the theoretical local asymptotic stability using command Reduce of Mathematica 12. The results are given in Table 4.

Table 4 Equilibria and their stability of system (11)