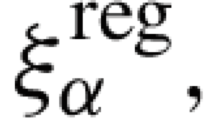Abstract
The frame-indifferent thermodynamically-consistent model of thermoviscoelasticity at large strain is formulated in the reference configuration by using the concept of the second-grade nonsimple materials. We focus on physically correct viscous stresses that are frame indifferent under time-dependent rotations. Also elastic stresses are frame indifferent under rotations and respect positivity of the determinant of the deformation gradient. The heat transfer is governed by the Fourier law in the actual deformed configuration, which leads to a nontrivial description when pulled back to the reference configuration. The existence of weak solutions in the quasistatic setting, that is inertial forces are ignored, is shown by time discretization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For a long time, thermoviscoelasticity was considered as a quite difficult problem even at small strains, mainly because of the nonlinear coupling with the heat-transfer equation which has no obvious variational structure; hence special techniques had to be developed. It took about two decades after the pioneering work by Dafermos [14] in one space dimension that first three-dimensional studies occurred (cf. for example [7, 12, 43]). The basic new ingredient was the \(L^1\)-theory for the nonlinear heat equation developed in [9, 11]. At large strains, in simple materials, the problem is still recognized to be very difficult even for the case of mere viscoelasticity without coupling with temperature, and only few results are available if the physically relevant frame-indifference is respected, as articulated by Ball [2], see also [3, 4]. In particular, local-in-time existence [27] or existence of measure-valued solutions [15, 18] are known for simple materials. Further examples in this direction are [52] for a general three-dimensional theory, but not respecting frame indifference and the determinant constraints, or [34] for a one-dimensional theory using the variational structure. While the static theory for large-strain elasticity developed rapidly after [2], there are still only few result for time-dependent processes respecting frame indifference as well as the determinant constraint. The first cases were restricted to rate-independent processes, such as elastoplasticity (cf. [31, 36]) or crack growth (cf. [16], see [35, Sec. 4.2] for a survey. Recently the case of viscoplasticity was treated in [38].
The main features of the model discussed in this work can be summarized in brief as follows: the thermoviscoelastic continuum is formulated at large strains in a reference configuration, that is the Lagrangian approach. The concepts of 2nd-grade nonsimple material is used, which gives higher regularity of the deformation. The heat transfer is modeled by the Fourier law in the actual deformed configuration, but transformed (pulled back) into the reference configuration for the analysis. Our model respects both static frame-indifference of the free energy and dynamic frame indifference for the dissipation potential. Moreover, the local non-selfpenetration is realized by imposing a blowup of the free energy if the determinant of the deformation gradient approaches 0 from above, however we do not enforce global non-selfpenetration. Also, we neglect inertial effects; cf. Remark 6.6 for more detailed discussion.
Let us highlight the important aspects of the presented model and their consequences:
-
\((\upalpha )\) The temperature-dependence of the free energy creates adiabatic effects involving the rate of the deformation gradient. To handle this, the Kelvin–Voigt-type viscosity is used to control the rate of the deformation gradient. In addition, we separate the purely mechanical part, cf. (2.15) below, which allows us to decouple the singularities of large-strain elasticity from the heat equation.
-
\((\upbeta )\) The heat transfer itself [and also the viscosity from \((\upalpha )\)] is clearly rate dependent and the technique of rate-independent processes supported by a variationally efficient energetic-solution concept cannot be used (which also prevents us from excluding possible global selfpenetration).
-
\((\upgamma )\) The equations for the solid continuum need to be formulated and analyzed in the fixed reference configuration but transport processes (here only the heat transfer) happen rather in the actual configuration and the pull-back procedure needs the determinant of the deformation gradient to be well away from 0. To achieve this, we exploit the concept of 2nd-grade nonsimple materials together with the results of Healey and Krömer [24], which allow us to show that the determinant for the deformation gradient is bounded away from 0, see Section 3.1.
-
\((\updelta \)) The transport coefficients depend on the deformation gradient because of the reasons in point \((\upgamma )\). For this, measurability in time is needed and thus the concept of global quasistatic minimization of deformation (as in rate-independent systems [35] or in viscoplasticity in [38]) would not be satisfactory; therefore we rather control the time derivative of the deformation, which can be done either by inertia (which is neglected in our work) or by the Kelvin–Voigt-type viscosity from \((\upalpha )\).
-
\((\upepsilon \)) The viscosity from \((\upalpha )\) must satisfy time-dependent frame indifference as explained in [1], thus it is dependent on the rate of the right Cauchy–Green tensor rather than on the rate of the deformation gradient itself. However, the adiabatic heat sources/sinks involve terms where the rate of the deformation gradient occurs directly. To control the latter by the former, we exploit results of Neff [39] in the extension by Pompe [41] for generalized Korn’s inequalities, see Section 3.2. Here, again the mentioned concept of 2nd-grade nonsimple materials is used to control the determinant of the deformation gradient, see \((\upgamma )\).
As mentioned above, our model heavily relies on the strain-gradient theories to describe materials, referred as nonsimple, or also multipolar or complex. This concept has been introduced long time ago, cf. [51] or also for example [8, 19, 28, 40, 46, 50] and in the thermodynamical concept also [6]. In the simplest scenario, which is also used here, the stored-energy density depends only on the strain \(F=\nabla y\) and on the first gradient \(\nabla F\) of the strain. This case is called 2nd-grade nonsimple material. Possible generalization using only certain parts of the 2nd gradient in the spirit of [25] still need to be explored.
The structure of the paper is as follows: in Section 2 we present the model in physical and mathematical terms. After the precise definition of our notion of solution, Theorem 2.2 provides the main existence result for global-in-time solutions for the large-strain thermoviscoelastic system, while Corollary 2.3 gives the corresponding existence result for viscoelasticity at large strain and at constant temperature, which, to the knowledge of the authors, is also new. A related result for isothermal large-strain viscoelasticity is derived in [20], but there the limit of small strains is treated.
After proving some auxiliary results about local invertibility of deformations and the Euler–Lagrange equations, a generalized Korn’s inequality, and about Chain rules in Section 3, we start the proof of the main result in Section 4 by introducing certain regularizations as well as a time-incremental approach. This is particularly constructed in such a split (sometimes called staggered) way that the deformation is first updated at fixed temperature from the previous time level and then the temperature is updated, where in some terms the old and in others the new deformation is used. Another important step in the analysis is the usage of an energy-like variable 
instead of temperature \(\theta \), which enables us to exploit the balance-law structure of the heat equation; cf. [30, 32] for arguments for the preference of energy in favor of temperature. After proving existence and a-priori estimates for such approximate solutions in Section 4, we continue by convergence in Section 5 by limiting the time discretization. Thus, as an intermediate result, Proposition 5.1 provides the existence of solutions \((y_\varepsilon ,\theta _\varepsilon )\) of the regularized problem. Eventually, in Section 6 we finally show that the limit \(\varepsilon _k\rightarrow 0\) for \((y_{\varepsilon _k},\theta _{\varepsilon _k}) \rightarrow (y,\theta )\) can be controlled in such a way that \((y,\theta )\) are the desired solutions. We conclude with a few remarks concerning potential generalizations and further applications of the methods.
2 Modeling of Thermoviscoelastic Materials in the Reference Configuration
We will use the Lagrangian approach and formulate the model in the reference (fixed) domain \(\varOmega \subset \mathbb {R}^d\) being bounded with a Lipschitz boundary \(\varGamma \). In fact, occasionally we will assume \(\varGamma \) smooth in order to reveal the classical formulation of the problem, cf. (2.13)–(2.14) based on the arguments (2.28)–(2.29) below. We assume \(d\geqq 2\) although, of course, the rather trivial case \(d=1\) works too if \(p\geqq 2\) is assumed, additionally to \(p>d\), in (2.30) below. We will consider a fixed time horizon \(T>0\) and use the notation \(I:=[0,T]\), \(Q:=I\times \varOmega \), and \(\varSigma :=I\times \varGamma \). For readers’ convenience, Table 1 summarizes the main nomenclature used throughout the paper.
To introduce our model in a broader context, we may define the total free energy and the total dissipation potential
respectively. The mechanical evolution part can then be viewed as an abstract gradient flow
cf. also [34, 52] for the isothermal case and [29] for the general case. The sum of the conservative and the dissipative parts corresponds to the Kelvin–Voigt rheological model in the quasistatic variant (neglecting inertia). The notation “\(\,\partial \,\)” is used for partial derivatives (here functional or later in Euclidean spaces), while \((\cdot )'\) will occasionally be used for functions of only one variable.
Writing (2.2) locally in the classical formulation, one arrives at the nonlinear parabolic 4th-order partial differential equation expressing quasistatic momentum equilibrium
where the viscous stress is \(\sigma _\mathrm {vi}=\sigma _\mathrm {vi}(F,\dot{F},\theta )\) and the elastic stress is \(\sigma _\mathrm {el}=\sigma _\mathrm {el}(F,\theta )\), while \({\mathfrak {h}}_\mathrm {el}\) is a so-called hyperstress arising from the 2nd-grade nonsimple material concept, cf. for example [40, 46, 51]. In view of the local potentials used in (2.2), we have
where \({\mathsf {G}}\in \mathbb {R}^{d\times d \times d}\) is a placeholder for \(\nabla F\).
An important physical requirement is static and dynamic frame indifference. For the elastic stresses, static frame indifference means that
for all \(R\in \mathrm {SO}(d)\), F and \({\mathsf {G}}\). For the viscous stresses, dynamic frame indifference means that
for all smoothly time-varying \(R{:}\,t\mapsto R(t)\in \mathrm {SO}(d)\), cf. [1]. Note that R may depend on t but not on \(x\in \varOmega \), since frame-indifference relates to superimposing time-dependent rigid-body motions.
In terms of the thermodynamic potentials \(\zeta \), \(\psi \), and \({\mathscr {H}}\), these frame indifferences read as
for R, F and \(\nabla F\) as above. These frame indifferences imply the existence of reduced potentials \({\widehat{\psi }}\), \({\widehat{\zeta }}\), and \(\widehat{{\mathscr {H}}}\) such that
where \({\mathsf {B}}={\mathsf {G}}^\top \!\cdot {\mathsf {G}} \in \mathbb {R}^{(d\times d)\times (d \times d)} \), and \(C\in \mathbb {R}^{d \times d}_\mathrm {sym}\) is the right Cauchy–Green tensor \(C=F^\top F\) with time derivative \(\dot{C}=\dot{F}^\top F+F^\top \dot{F}\). More specifically, denoting \({\mathsf {G}}=[{\mathsf {G}}_{\alpha ij}]\) the placeholder for \(\frac{\partial }{\partial x_j}F_{\alpha i}\) with \(F_{\alpha i}\) the placeholder for \(\frac{\partial }{\partial x_i}y_{\alpha }\), the exact meaning is \( [ {\mathsf {G}}^\top \! \cdot {\mathsf {G}}]_{ijkl} := \sum _{\alpha =1}^d{\mathsf {G}}_{\alpha ij}{\mathsf {G}}_{\alpha kl}\) and \([F^\top F]_{ij}:=\sum _{\alpha =1}^dF_{\alpha i}F_{\alpha j}\). The ansatz (2.7) also means that
The simplest choice, which is adopted in this paper for avoiding unnecessary technicalities, is that the viscosity \(\sigma _\mathrm {vi}\) is linear in \(\dot{C}\). This is the relevant modeling choice for non-activated dissipative processes with rather moderate rates (in contrast to activated processes like plasticity having nonsmooth potentials that are homogeneous of degree 1 in a small-rate approximation). This linear viscosity leads to a potential which is quadratic in \(\dot{C}\), viz.
Although for this choice the material viscosity is linear, the geometrical nonlinearity arising from large strains is still a vital part of the problem due to the requirement of frame indifference. Note that \(\sigma _\mathrm {vi}(F,\dot{F},\theta )\) necessarily depends on F if we express \(\dot{C}\) in terms of the velocity gradients \(\dot{F}\), even if \(\mathbb {D}\) is constant: \(\sigma _\mathrm {vi}(F,\dot{F},\theta ) = 2F \mathbb {D}(C,\theta )(\dot{F}^\top F{+}F^\top \dot{F})\). While we will be able to handle general dependence on F, it will be a crucial restriction that \(\dot{F} \mapsto \sigma _\mathrm {vi}(F,\dot{F},\theta )\) is linear.
Furthermore, the specific dissipation rate can be simply identified in terms of \({\widehat{\zeta }}\) as
For our choice (2.9), we simply have \(\xi (F,\dot{F},\theta )=\mathbb {D}(C,\theta )\dot{C}{:}\dot{C} =2{\widehat{\zeta }}(C,\dot{C},\theta )=2\zeta (F,\dot{F},\theta )\).
In brief, the standard thermodynamical arguments start from the free energy density \(\psi \) and the definition of entropy via \(s=-\partial _{\theta }^{}\psi \) (here \({\mathscr {H}}\) does play no role as it is chosen to be independent of \(\theta \)) and the entropy equation
with the dissipation rate \(\xi \) from (2.10) and the heat flux \(\vec {q}\). We further use the formula \(\dot{s}=-\partial _{\theta \theta }^2\psi \,\dot{\theta }-\partial _{F\theta }^2\psi {:}\dot{F}\) and the Fourier law formulated in the reference configuration
which will be specified later in (2.24). Altogether, we arrive at the coupled system
on Q. We complete (2.13) by some boundary conditions. For simplicity, we only consider a mechanically fixed part \({\varGamma }_{\textsc {D}}\) time independent undeformed (that is identity) while the whole boundary is thermally exposed with a phenomenological heat-transfer coefficient \(\kappa \geqq 0\):
where \(\vec n\) is the outward pointing normal vector, and \(\theta _\flat \) is a given external temperature. Moreover, following [10] the surface divergence “\(\mathrm {div}_{\scriptscriptstyle \text {S}}^{}\)” in (2.14a) is defined as \(\mathrm {div}_{\scriptscriptstyle \text {S}}^{}(\cdot )=\mathrm {tr}\big (\nabla _{\scriptscriptstyle \text {S}}^{}(\cdot )\big )\), where \(\mathrm {tr}(\cdot )\) denotes the trace and \(\nabla _{\scriptscriptstyle \text {S}}^{}\) denotes the surface gradient given by \(\nabla _{\scriptscriptstyle \text {S}}^{}v=({\mathbb {I}}- \vec n{\otimes }\vec n)\nabla v= \nabla v-\frac{\partial v}{\partial \vec {n}}\vec {n}\). See (2.29) for a short mathematical derivation of the boundary conditions (2.14a) and (2.14c), and [48, pp. 358–359] for the mechanical interpretation in second-order materials.
In order to facilitate the subsequent mathematical analysis, we assume a rather weak thermal coupling through the free energy (together with the coupling through the temperature-dependent viscous dissipation). To distinguish the particular coupling thermo-mechanical term from the purely mechanical one, we consider the explicit ansatz
In applications, the internal energy e given by Gibbs’ relation
is often balanced. Here, we rather use the thermal part of the internal energy \(w:=e-\varphi (F)\). In view of the ansatz (2.15), we have
Note that 
is the primitive function of the specific heat \(c_\mathrm {v}(F,\cdot )\) calibrated as 
, in accord with the fact that \(w=e-\varphi (F)=e-\psi (F,0)\). The heat-transfer equation (2.13b) simplifies as
In particular, the purely mechanical stored energy \(\varphi \) does not occur in (2.16) and does not influence the heat production and transfer in (2.17). This is crucial because in the first step of the analysis we are not able to control the determinant of \( \nabla y\), but \( \partial _F \varphi (\nabla y,\theta )\) blows up for \(\det \nabla y \searrow 0 \). In contrast, we are able to assume that \(F\mapsto \partial _F \phi (F,\theta )\) behaves globally nicely, see (2.30b) and (2.30c).
The energetics of the system (2.13)–(2.14) can be best described by introducing additional energy functionals as follows:
A mechanical energy balance is revealed by testing (2.13a) by \(\dot{y}\) and (2.13b) by 1, and using the boundary conditions after integration over \(\varOmega \) and using the Green formula twice together with another \((d{-}1)\)-dimensional Green formula over \(\varGamma \) for (2.13a) and once again Green’s formula for (2.13b). The last mentioned technique is related with the concept of nonsimple materials; for the details about how the boundary conditions are handled see for example [44, Sect. 2.4.4]. This test of (2.13a) gives the mechanical energy balance:
Using \(\sigma _\text {el} = \partial _F\varphi + \partial _F \phi \) and integrating in time leads to the relation
which will be very useful for obtaining a priori estimates in the sections to follow.
Next, we test the heat equation in its simplified form (2.17) together with the boundary conditions (2.14d) by the constant function 1 (that is we merely integrated over \(\varOmega \)) and add the result to (2.20). After major cancellations we obtain the total energy balance:
In particular, we see that the total energy is conserved up to the work induced by the external loadings or the flux of heat through the boundary.
From the entropy equation (2.11), we can read the total entropy balance (the Clausius–Duhem inequality):
This articulates, in particular, the second law of thermodynamics that the total entropy in the isolated systems (that is here \(\vec {q}=0\) on \(\varGamma \)) is nondecreasing with time provided \(\mathcal {K}=\mathcal {K}(\nabla y,\theta )\) is positive semidefinite and the dissipation rate is non-negative.
It is certainly a very natural modeling choice that Fourier’s law is formulated in the actual (also called the deformed) configuration in a simple form, namely the actual heat flux is given by
with the heat-conductivity tensor \({\mathbb {K}}= {\mathbb {K}}(x,\theta )\) considered as a material parameter possibly dependent on \(x\in \varOmega \). We transform (that is pull back) this Fourier law to the reference configuration via \(\vec q = ({\mathrm {Cof}}\, F^\top ) \vec {{\mathsf {q}}}\), because fluxes should be considered as \((d{-}1)\)-forms. Writing Fourier’s law in material coordinates as \(\vec q(x)={\mathcal {K}}(x) \nabla \theta \) a comparison with (2.23) leads to the usual transformation rule for 2nd-order contra-variant tensors, namely
if \(\det F>0\), whereas the case \(\det F\leqq 0\) is considered nonphysical, so \(\mathcal {K}\) is then not defined. Here we used the standard shorthand notation \(F^{-\top }=[F^{-1}]^\top =[F^\top ]^{-1}\) and also the algebraic formula \(F^{-1}=({\mathrm {Cof}}\, F^\top )/\det F\). In what follows, we omit explicit x-dependence for notational simplicity. Let us emphasize that in our formulations \(\nabla \theta \) is not treated as a vector, but a contravariant 1-form. Starting from \(\theta (x)=\uptheta (y(x))\) the chain-rule gives \( \nabla \theta (x) = \nabla y(x)^\top \nabla _Y\varvec{\theta }(y(x))\). It should be noted that (2.23) is a rather formal argumentation, assuming injectivity of the deformation y and thus existence of \(y^{-1}\), which is however not guaranteed in our model; anyhow, handling only local non-selfpenetration while ignoring possible global selfpenetration is our modeling approach often accepted in engineering, too, see for example [49, p. 433], [47, Sec. 3.1], and [48, p. 293].
For the isotropic case \({\mathbb {K}}(\theta )=\varkappa (\theta )\mathbb {I}\), relation (2.24) can also be written by using the right Cauchy–Green tensor \(C=F^\top F\) as \(\mathcal K=\det (F)\varkappa (\theta )C^{-1}\), cf. for example [17, Formula (67)] or [23, Formula (3.19)] for the mass instead of the heat transport. In principle, \({\mathbb {K}}\) in (2.23) itself may also depend on \(C=F^\top F\), which we omitted to emphasize that \(\mathcal {K}\) in (2.24) will depend on F even if \({\mathbb {K}}\) itself will not.
In what follows, we will use the (standard) notation for the Lebesgue \(L^p\)-spaces and \(W^{k,p}\) for Sobolev spaces whose kth distributional derivatives are in \(L^p\)-spaces and the abbreviation \(H^k=W^{k,2}\). The notation \(W^{1,p}_{\mathrm{D}}\) will indicate the closed subspace of \(W^{1,p}\) with zero traces on \({\varGamma }_{\textsc {D}}\) and set \(p'=p/(p{-}1)\). Thus, for example,
For the fixed time interval \(I=[0,T]\), we denote by \(L^p(I;X)\) the standard Bochner space of Bochner-measurable mappings \(I\rightarrow X\) with X a Banach space. Also, \(W^{k,p}(I;X)\) denotes the Banach space of mappings from \(L^p(I;X)\) whose k-th distributional derivative in time is also in \(L^p(I;X)\). The dual space to X will be denoted by \(X^*\). Moreover, \(C_{\mathrm{w}}(I;X)\) denotes the Banach space of weakly continuous functions \(I\rightarrow X\). The scalar product between vectors, matrices, or 3rd-order tensors will be denoted by “\(\,\cdot \,\)”, “ : ”, or “\(\;\vdots \!\;\)”, respectively. Finally, in what follows, K denotes a positive, possibly large constant.
We consider an initial-value problem, imposing the initial conditions
Having in mind the form (2.17) of the heat equation, we can now state the following definition for a weak solution:
Definition 2.1
(Weak solution). A couple \((y,\theta ):Q=[0,T]{\times }\varOmega \rightarrow \mathbb {R}^d\times \mathbb {R}\) is called a weak solution to the initial-boundary-value problem (2.13) & (2.14) & (2.26) if \((y,\theta )\in C_{\mathrm{w}}(I;W^{2,p}(\varOmega ;\mathbb {R}^d))\times L^1(I;W^{1,1}(\varOmega ))\) with \(\nabla \dot{y}\in L^2(Q;\mathbb {R}^{d\times d})\), if \(\min _Q\det \nabla y>0\) and \(y|_{{\varSigma }_{\textsc {D}}}= \text { identity}\), and if it satisfies the integral identity
for all smooth \(z:Q\rightarrow \mathbb {R}^d\) with \(z=0\) on \({\varSigma }_{\textsc {D}}\) together with \(y(0,\cdot )=y_0\), and if
for all smooth \(v{:}\,Q\rightarrow \mathbb {R}\) with \(v(T)=0\), where 
is defined in (2.16).
At first sight, it seems that (2.27a) is not suited to apply the test function \(z = \dot{y}\), which is the natural and necessary choice for deriving energy bounds. Obviously, we will not be able to obtain enough control on \(\nabla ^2\dot{y}\). However, using the abstract chain rules provided in Section 3.3 this problem can be handled by extending \({\mathcal {H}}(y)=\int _\varOmega {\mathscr {H}}(\nabla ^2y)\,\mathrm {d}x \) to a lower semicontinuous and convex functional on \(H^1(\varOmega ;\mathbb {R}^d)\) by setting it \(\infty \) outside \(W^{2,p}(\varOmega ; \mathbb {R}^d)\), see the rigorous proof of (5.9) in Step 3 of the proof of Proposition 5.1.
It will be somewhat technical to see that the weak formulation (2.27a) is indeed selective enough, in the sense that for sufficiently smooth solutions one can indeed obtain the classical formulation (2.13) together with the boundary conditions (2.14), cf. also [44, Sect. 2.4.4]. In particular, abbreviating \(\sigma =\sigma _\mathrm {vi}(\nabla y,\nabla \dot{y},\theta ) +\sigma _\mathrm {el}(\nabla y,\theta )\), integrating by part once, and using the boundary conditions (2.14a,c) yields
We now want to show how the strong form (2.13a) and the associated boundary conditions (2.14a,c) follow from (2.28). For this goal, we apply Green’s formula in the opposite direction to remove \(\nabla \) in front of the test function z. Using also the orthogonal decomposition of \(\nabla z=\nabla _{\scriptscriptstyle \text {S}}^{}z + \frac{\partial }{\partial \vec {n}}z\otimes \vec {n} \) involving the surface gradient \(\nabla _{\scriptscriptstyle \text {S}}^{}z\) and writing shortly \({\mathfrak {h}}\) for \({\mathfrak {h}}_\mathrm {el}(\nabla ^2y)\in \mathbb {R}^{d\times d \times d}\), relation (2.28) leads to the identity
Using the surface divergence \(\mathrm {div}_{\scriptscriptstyle \text {S}}^{}\) and the projection \(P_{\scriptscriptstyle \text {S}}^{}:A\mapsto A-A\vec {n} \otimes \vec {n} \) to the tangential part, we obtain the integration by parts formula (cf. [10] or [48, pp. 358–359])
where the surface \(\varGamma \) is now assumed to be sufficiently smooth. Using this with \(A={\mathfrak {h}}\vec {n}\) for the previous relation we find
where we have used \(z=0\) on \({\varSigma }_{\textsc {D}}=\varSigma {\setminus } {\varSigma }_{\textsc {N}}\). Now, taking z’s with a compact support in Q, we obtain the equilibrium (2.13a) in the bulk. Next taking z’s with zero traces on \(\varSigma \) but general \( \frac{\partial z}{\partial \vec {n}}\), we obtain (2.14c). Note that the latter condition implies \(P_{\scriptscriptstyle \text {S}}^{}({\mathfrak {h}}\vec {n})={\mathfrak {h}}\vec {n} - \big ({\mathfrak {h}}:(\vec {n}{\otimes }\vec {n})\big )\otimes \vec {n} = {\mathfrak {h}}\vec {n}\). Hence, taking finally general z’s, we obtain (2.14a), as \(P_{\scriptscriptstyle \text {S}}^{}\) can be dropped because of (2.14c).
Moreover, also note that, from the integral identity (2.27b), one can read 
from which \(\theta (0)=\theta _0\) follows when taken the invertibility of 
and \(y(0)=y_0\) into account.
Now we exploit the decomposition (2.15) of \(\psi \) into \(\varphi \) and \(\phi \), which allows us to impose coercivity assumptions for the purely elastic part \(\varphi \) that are independent of those for \(\phi \):
where \(\mathrm {GL}^+(d)\) denotes the set of matrices in \(\mathbb {R}^{d\times d}\) with positive determinant. The last assumption in (2.30c) means that \(c_\mathrm {v}\) together with \(c_\mathrm {v}^{-1}\) are bounded, which is a major restriction. However, it allows for a rather simple estimation in Lemma 6.3; for alternative, more general situations dealing with increasing \(c_\mathrm {v}(\cdot )\) we refer to [26, Sec. 8.3].
The function 
defined in (2.16) satisfies 
by (2.15). Moreover, we have 
. Hence assumption (2.30c) implies, for all \( F\in \mathrm {GL}^+(\mathbb {R}^d) \), the two-sided estimates
Assumptions (2.30b,c) make the thermomechanical coupling through \(\phi \) rather weak in order to allow for a simple handling of the mechanical part independently of the temperature. These restrictive assumptions are needed for our specific and simple way of approximation method rather than for the problem itself. E.g. the assumption in (2.30b) is used to facilitate the estimate (4.12), which allows us to control the difference between \(\int _\varOmega \phi (\nabla y^k,\theta ) \,\mathrm {d}x \) and \(\int _\varOmega \phi (\nabla y^{k-1},\theta ) \,\mathrm {d}x \) in terms of \({\mathcal {M}}(y^k)\), \({\mathcal {M}}(y^{k-1})\), and \(\Vert \nabla y^k{-}\nabla y^{k-1}\Vert _{L^2}^2\). Moreover, after having derived uniform bounds on \(|\nabla y^k|\) it will be exploited to show that the thermo-coupling stress \(\partial _F\phi \) is bounded. Finally, (2.30d) and (2.30h) make the stored energy finite at time \(t=0\).
It will be important that \(\partial _F^{}\phi (F,\theta )\) vanishes for \(\theta =0\) [which follows from (2.15)], so that temperature stays non-negative if \(\theta _0\geqq 0\) and \(\theta _\flat \geqq 0\), as assumed.
We now state our main existence results, which will be proved in the following Sections 4–6. The method will be constructive, avoiding non-constructive Schauder fixed-point arguments, however some non-constructive attributes such as selections of converging subsequences will remain. More specifically, the proof is obtained by first making the a priori estimates for time-discretized solutions in Proposition 4.2, and then deriving an existence result for time-continuous solutions of an \(\varepsilon \)-regularized problem, see Proposition 5.1. Finally, Proposition 6.4 provides convergence for \(\varepsilon \rightarrow 0\).
Theorem 2.2
(Existence of energy-conserving weak solutions). Assume that the conditions in (2.30) hold. The original initial-boundary-value problem (2.13)–(2.14)–(2.26) with \(\mathcal {K}\) from (2.24) possesses at least one weak solution \((y,\theta )\) in the sense of Definition 2.1. In addition, these solutions satisfy \(\nabla \theta \in L^r(Q;\mathbb {R}^d)\) for all \(1\leqq r<(d{+}2)/(d{+}1)\), the mechanical energy balance (2.19), and the total energy balance (2.21).
As mentioned in the introduction, a lot of publications are devoted to the simpler isothermal viscoelasticity at large strain, yet, in the multi-dimensional case, they do not satisfy all the necessary physical requirements. It is therefore worthwhile to present a version of our existence result by restricting it to this isothermal case, for which a lot of assumptions are irrelevant or simplify. In particular, (2.15) simplifies as \(\psi (F,\theta )=\varphi (F)\). Of course, our theory only works because we are using a non-degenerate second-grade material, where the energy contribution \({\mathcal {H}}(y):=\int _\varOmega {\mathscr {H}}(\nabla ^2 y)\,\,\mathrm {d}x \) generates enough regularity to handle the geometric and physical nonlinearities. To the best of the authors knowledge, even the result for isothermal viscoelasticity is new.
A similar regularization approach to isothermal large-strain viscoelasticity was considered in [20], where the \({\mathcal {H}}(y)\) is multiplied with a small parameter that vanishes slower than the loading. Hence, the authors are able to show that their solutions are sufficiently close to the identity which allows them to exploit a simpler Korn’s inequality obtained by a perturbation argument. Hence, to the best of the authors’ knowledge the following result is the first that allows for truly large strains:
Corollary 2.3
(Viscoelasticity at constant temperature). Let \(\varphi \) satisfy (2.30a), and let (2.30d-e,g-h) be satisfied with \({\widehat{\zeta }}={\widehat{\zeta }}(C,\dot{C})\) and with \(\psi =\varphi \). Then, the initial-boundary-value problem (2.13a)–(2.14a)–(2.26) (with \(\theta \) ignored) possesses at least one weak solution y in the sense that the integral identity (2.27a) holds. In addition, the mechanical energy balance (2.20) holds with \(\xi =\xi (F,\dot{F})\) and without the last term involving \(\partial _F^{}\phi \).
Before going into the proof of our main result, we show that our conditions are general enough for a series of nontrivial applications:
Example 2.4
(Classical thermomechanical coupling). The classical example of a free energy in thermomechanical coupling is given in the form
that is \(\phi (F,\theta )\) involves a term in the product form \(-a(\theta )\varphi _1(F)\). For the purely mechanical part we may take the polyconvex energy \(\varphi (F)= c_1 |F|^s + c_2/(\det F)^q\) for \(\det F>0\) and \(\infty \) otherwise. For the thermomechanical coupling we obtain \(c_\text {v}(F,\theta ) = - \theta \partial _{\theta \theta }^2 \psi (F,\theta )= c + a''(\theta )\varphi _1(F)\), thus to have positivity of the heat capacity \(c_\text {v}\), we assume \(a''(\theta )\geqq 0\) and \(\varphi _1(F)\geqq 0\). Moreover, we have
Thus, we see that all assumptions in (2.30) can easily be satisfied, for example by choosing \(a(\theta )=(1{+}\theta )^{-\alpha }\) with \(\alpha >0\), which is smooth bounded and convex, and taking any \(\phi _1 \in C^2_\text {c}(\mathbb {R}^{d\times d})\).
Example 2.5
(Phase transformation in shape-memory alloys). An interesting example of a free energy \(\psi \) occurs in the modeling of austenite-martensite transformation in so-called shape-memory alloys:
cf. for example [42] and references therein. Here a denotes the volume fraction of the austenite versus martensite which is supposed to depend only on temperature. Of course, this is only a rather simplified model. For, \(\psi _0(\theta )= c\theta (1{-}\log \theta )\) it complies with the ansatz (2.32) with \(\varphi (F)=\varphi _{_\mathrm {A}}(F)\) and \(\varphi _1(F)= \varphi _{_\mathrm {M}}(F){-}\varphi _{_\mathrm {A}}(F)\). The heat capacity then reads as
To ensure its positivity, \(\psi _0\) has to be strictly concave in such a way that \(\psi _0''(\theta )\leqq K/\theta \) and then \(\inf _{(F,\theta )}\theta a''(\theta )[\varphi _{_\mathrm {A}}{-}\varphi _{_\mathrm {M}}](F)+K>0\) has to (and can) be ensured by suitable modeling assumptions.
Remark 2.6
(Thermal expansion). Multiplicative decomposition \(F=F_\mathrm {el}F_\mathrm {th}\) with the “thermal strain” \(F_\mathrm {th}=\mathbb {I}/\mu (\theta )\) and the elastic strain \(F_\mathrm {el}\) which enters the elastic part of the stored energy \(\varphi \). This would lead to
Unfortunately, (2.33) is inconsistent with the ansatz (2.15) because the contribution \(\varphi \) which has been important for our analysis due to uniform coercivity, cannot be identified in (2.33).
3 A Few Auxiliary Results
In this subsection we provide a series of auxiliary results that are crucial to tackle the difficulties arising from large-strain theory. First, we show how the theory developed by Healey and Krömer [24] allows us to derive a positive lower bound for \(\det \nabla y\) from the a priori bounds for the elastic energy \({\mathcal {M}}(y,\theta )\). This can then be used to establish the validity of the Euler–Lagrange equations and a useful \(\lambda \)-convexity result, which is needed for obtaining optimal energy estimates. Second, we provide a version of Korn’s inequality from Pompe [41] that allows us to obtain dissipation estimates via \({\mathcal {D}}(y,\dot{y},\theta ) \geqq c_0 \Vert \dot{y}\Vert ^2_{H^1(\varOmega )} \). Finally, in Section 3.3 we provide abstract chain rules as derived in [37, Sec. 2.2] that allow us to derive energy balances like (2.20) from the corresponding weak equations.
3.1 Local Invertibility and Euler–Lagrange Equations
A crucial point in the large-strain theory is the blow-up of the energy density \(\psi (F,\theta )\) for \(\det F\searrow 0\). Thus, it is desirable to find a suitable positive lower bound for \(\det \nabla y(t,x)\). The following theorem is an adaptation of the result in [24, Thm. 3.1].
Theorem 3.1
(Positivity of determinant). Assume that the mechanical energy \({\mathcal {M}}{:}\,W^{2,p}(\varOmega ;\mathbb {R}^d) \rightarrow \mathbb {R}_\infty \) satisfies the assumptions in (2.30a) and (2.30d). Then, for each \(C_M>0\) there exists \(C_\mathrm {HK}>0\) such that all \(y\in {\mathcal {Y}}_\mathrm {id}\) with \({\mathcal {M}}(y)\leqq C_M\) satisfy
Proof
We give the full proof, since our mixed boundary conditions are not covered in [24]. From \({\mathcal {M}}(y)\leqq C_M\) and the coercivities of \(\varphi \) and \({\mathscr {H}}\) we obtain \(\det \nabla y\geqq 0\) almost everywhere in \(\varOmega \) and the a priori bounds
Together with the Dirichlet boundary conditions in \({\mathcal {Y}}_\mathrm {id}\) we obtain an a priori bound for y in \(W^{2,p}(\varOmega ;\mathbb {R}^d)\) and hence also in \(C^{1,\lambda }(\varOmega ;\mathbb {R}^d)\), where \(\lambda = 1-d/p>0\). This proves the first two assertions.
In particular, the function \(\delta {:}\,x \mapsto \det (\nabla y(x))\) is Hölder continuous as well with \(\Vert \delta \Vert _{C^\alpha }\leqq C_M^{(2)}\). Since \(\varOmega \) is a bounded Lipschitz domain, there exist a radius \(r_*>0\) and a constant \(\alpha _*>0\) such that for all \(x\in \overline{\varOmega }\) the sets \(B_{r_*}(x)\cap \overline{\varOmega }\) contain an interior cone \({\mathsf {C}}(x)=\big \{ x{+}z\, ;\ 0<|z|<r_*,\ \frac{1}{|z|}z \in A(x) \big \}\) where the set \(A(x)\subset {\mathbb {S}}^{d-1}\) of cone directions has a surface measure \(\int _{A(x)} 1 \,\mathrm {d}S \geqq \alpha _*\). Thus, using the Hölder continuity
\(\lambda =1-d/p \geqq d/q\) [see (2.30)], and \(|y{-}x|=r\leqq r_*\) for \(y \in {\mathsf {C}}(x)\), we can estimate as follows:
This yields the lower bound \(\delta (x)^q \geqq r_*^d \exp \big ( {-}C^{(1)}_M/c^{(5)}\big )\), viz. the third assertion in (3.1).
The last assertion follows via the implicit function theorem. \(\quad \square \)
The most important part of the above result is that the determinant of \(\nabla y\) is bounded away from 0. Hence, the function \(f \mapsto \varphi (F)\), which blows up for \(\det F \searrow 0\), is evaluated only in a compact subset of \(\mathrm {GL}^+(d) \subset \mathbb {R}^{d \times d}\) such that \(\partial _F\phi \) and \(\partial ^2 \varphi \) exist. Again following [24, Cor. 3.3] we obtain the Gateaux differentiability of \({\mathcal {M}}\) and as well as a useful \(\Lambda \)-semiconvexity result.
Proposition 3.2
(Gateaux derivative and \(\Lambda \)-semiconvexity). Assume that \({\mathcal {M}}\) satisfies (2.30a) and (2.30d). Then, at each point \(y\in {\mathcal {Y}}_\mathrm {id}\) with \({\mathcal {M}}(y)<\infty \) the Gateaux derivative of \({\mathcal {M}}\) in all directions \(h\in {\mathcal {Y}}_0:= \big \{\, v\in W^{2,p}(\varOmega ;\mathbb {R}^d)\,; \, v|_{{\varGamma }_{\textsc {D}}}\, \big \} \) exists and has the form
Moreover, for each \(C_M>0\) there exists \(\Lambda (C_M)>0\) such that for all \(y^{(1)},y^{(2)} \in {\mathcal {Y}}_\mathrm {id}\) with \({\mathcal {M}}(y^{(j)}) \leqq C_M \) and \(\Vert \nabla y^{(1)}-\nabla y^{(2)}\Vert _{ L^\infty (\varOmega ;\mathbb {R}^d) } \leqq 1/ C_M \) we have \(\Lambda (C_M)-\)convexity
Proof
We decompose \({\mathcal {M}}={\mathcal {H}}+\varPhi _\mathrm {el}\), see (2.18b). The differentiability of the convex functional \(y \mapsto {\mathcal {H}}(y)\) on \(W^{2,p}(\varOmega ;\mathbb {R}^d)\) is standard and follows from (2.30d). For treating \(\varPhi _\mathrm {el}\) we use the embedding \(W^{2,p}(\varOmega ) \subset C^{1,\lambda }(\varOmega )\) and exploit the result \(\det \nabla y(x)\geqq 1/C_\mathrm {HK}\) from Theorem 3.1. For all \(h\in W^{2,p}_{{\varGamma }_{\textsc {D}}}(\varOmega ;\mathbb {R}^d)\) we find a \(t_*>0\) such that \(\det \big ( \nabla (y{+}th)(x)\big ) > 1/(2C_\mathrm {HK}) \) for all \(t\in [-t_*,t_*]\) and all \(x \in \varOmega \). Hence,
and the limit passage is trivial as the convergence in the integrand is uniform.
To derive (3.3) we observe that the convexity of \({\mathscr {H}}\) implies
To treat the functional \(\varPhi _\mathrm {el}\) we apply Theorem 3.1 to \(y^{(1)}\) and \(y^{(2)}\), which implies the pointwise bounds
Clearly there is a \(\delta >0\) such that
We denote by \(-\Lambda _*\) the minimum of the smallest eigenvalue of the matrices \(\partial _{FF}^2 \varphi (F)\) where \(F\in \mathbb {R}^{d \times d} \) runs through the compact set given by \( |F|\leqq C_\mathrm {HK}\) and \(\det F\geqq 1/(2C_\mathrm {HK})\). Hence, assuming \(\Vert \nabla y^{(2)}{-}\nabla y^{(2)}\Vert _{L^\infty } \leqq \delta \) we find
This establishes the result with \(\Lambda (C_M):= \max \{ C_\mathrm {HK}, 1/\delta , \Lambda _*/2\}\). \(\quad \square \)
3.2 A Generalized Korn’s Inequality
The following result will be crucial to show that the nonlinear viscosity depending on \( F=\nabla y\) really controls the \(H^1\)-norm of the rate \(\dot{y}\). It relies on Neff’s generalization [39] of the Korn inequality, in the essential improvement obtained by Pompe [41].
Theorem 3.3
(Generalized Korn’s inequality). For a fixed \(\lambda \in {]0,1[}\) and positive constants \(K>1\) define the set
Then, for all \(K>1\) there exists a constant \(c_K>0\) such that for all \(F\in {\mathsf {F}}_K\) we have
Proof
In [41, Thm. 2.3] it is shown that (3.4) holds for each fixed \(F\in {\mathsf {F}}_K\) with \(c_K\) possibly dependent on F. Let us denote by \(c(F)>0\) the best possible constants for the given F. By a perturbation argument it is easy to see that the mapping \(F\mapsto c(F)\) is continuous with respect to the \(L^\infty \) norm in \(C^0(\overline{\varOmega };\mathbb {R}^{d \times d})\). Since \({\mathsf {F}}_K\) is a compact subset of \(C^0(\overline{\varOmega };\mathbb {R}^{d \times d})\) the infimum of c on \({\mathsf {F}}_K\) is attained at some \(F_*\in {\mathsf {F}}_K\) by Weierstraß’ extremum principle. Because of \(c(F)\geqq c(F_*)>0\), we conclude that (3.4) holds with \(c_K=c(F_*)\). \(\quad \square \)
We emphasize that estimate (3.4) is not valid if F is not continuous, see [41, Thm. 4.2]. This shows that the \(W^{2,p}\)-regularity of y is crucial to control the rate of the strain \(\nabla \dot{y}\), which is necessary to handle the thermomechanical coupling. The following corollary combines Theorems 3.1 and 3.3, by using the compact embedding \(W^{2,p}(\varOmega ;\mathbb {R}^d) \subset C^{1,\lambda }(\varOmega ;\mathbb {R}^d)\).
Corollary 3.4
(Uniform generalized Korn’s inequality on sublevels). Given any \(C_M>0\) there exists a \(\overline{c}_K>0\) such that for all \(y \in {\mathcal {Y}}_\mathrm {id}\) with \({\mathcal {M}}(y)\leqq C_M\) we have
3.3 Chain Rules for Energy Functionals
Abstract chain rules for energy functionals \({\mathcal {J}}{:}\,X\rightarrow \mathbb {R}_\infty :=\mathbb {R}{\cup } \{\infty \}\) on a Banach space concern the question under what conditions for an absolutely continuous curve \(z{:}\,[0,T]\rightarrow X\) the composition \(t \mapsto {\mathcal {J}}(z(t))\) is absolutely continuous and satisfies \(\frac{\,\mathrm {d}}{\,\mathrm {d}t} {\mathcal {J}}(z(t))= \langle \varXi (t), \dot{z}(t)\rangle \) for \(\varXi \in {\overline{\partial }} {\mathcal {J}}(z(t))\), where \({\overline{\partial }}\) denotes a suitable subdifferential. In particular, this implies
The case that X is a Hilbert space and \({\mathcal {J}}\) is convex and lower semicontinuous goes back to [13, Lem. 3.3], see also [5, Lemma 4.4].
Proposition 3.5
(Chain rule for convex functionals in a Hilbert space). Let X be a Hilbert space and \({\mathcal {J}}{:}\,X\rightarrow \mathbb {R}_\infty :=\mathbb {R}{\cup } \{\infty \}\) a lower semicontinuous and convex functional. If the functions \(z{:}\,[0,T]\rightarrow X\) and \(\varXi {:}\,[0,T]\rightarrow X^*\) satisfy
where \(\partial {\mathcal {J}}\) denotes the convex subdifferential, then
A first generalization to Banach spaces X with separable dual \(X^*\) is given in [53, Prop.XI.4.11]. We provide a slight generalization of the results in [37, Sec. 2.2] that work for arbitrary reflexive Banach spaces and include also certain nonconvex functionals. The functional \({\mathcal {J}}\) is called locally semiconvex, if for all z with \({\mathcal {J}}(z)< \infty \) there exist \( \Lambda (z)\geqq 0\) and a ball \(B_r(z)=\{\, {\widehat{z}}\in X\,; \, \Vert {\widehat{z}}{-}z\Vert _X\leqq r \, \} \) with \(r={\widehat{r}}(z)\) such that the restriction \({\mathcal {J}}|_{B_r(z)} \) is \(\Lambda \)-semiconvex, viz.
By \(\overline{\partial }{\mathcal {J}}\) we denote the Fréchet subdifferential which is defined by
The next results follows by a simple adaptation of the proof of [37, Prop. 2.4].
Proposition 3.6
(Chain rule for locally semiconvex functionals). Consider a separable reflexive Banach space, \(q\in {]1,\infty [}\) with \(q'=q/(q{-}1)\), and \({\mathcal {J}}{:}\,X\rightarrow \mathbb {R}_\infty \) a lower semicontinuous and locally semiconvex functional. If the functions \(z\in W^{1,q}([0,T]; X)\) and \(\varXi \in L^{q'}([0,T];X^*) \) satisfy
then
Proof
The result follows by the fact that the image of z lies in \(\mathrm {dom}{\mathcal {J}}=\{\, z\in X\,; \, {\mathcal {J}}(z)<\infty \, \} \) and is compact in X. Hence there is one \(\Lambda _*<\infty \) and one \(r_*>0\) that provides \(\Lambda _*\) semiconvexity on \(B_{r_*}(z(t))\) for all \(t\in [0,T]\). Thus, the results in the proof of [37, Prop. 2.4] can be applied when choosing \(\omega ^R({\widehat{z}},z)=\Lambda _*\Vert {\widehat{z}}{-}z\Vert _X\) there and using the fact that all needed arguments are local and rely only on information of \({\mathcal {J}}\) in a neighborhood of the image of the curve \( t \mapsto z(t) \). \(\quad \square \)
4 Time Discretization of a Regularized Problem
Before we construct solutions by a suitable time-discretization, we introduce regularizations in two points. Firstly, we add a linear viscous damping which allows us to obtain simple a priori bounds for the strain rate \(\nabla \dot{y}\), because in the first steps of the construction we are not yet in a position to exploit the generalized Korn inequality of Theorem 3.3. Secondly, we modify the heat production induced by the viscous damping, which in the physically correct form leads to an \(L^1\)-source term, that cannot be handled in the first steps of the construction below.
Hence, introducing the regularization parameter \(\varepsilon >0\) we consider the coupled system
where 
is from (2.16) and \(\mathcal {K}\) from (2.24). This system is defined on Q and is complemented with regularized boundary and initial conditions
This system is solved by a time discretization. For this, we consider a constant time step \(\tau >0\) such that \(T/\tau \) is an integer, leading to an equidistant partition of the considered time interval [0, T]. (However, varying time-steps can be easily implemented because we will always consider only first-order time differences and one-step formulas.)
For the time discretization of the regularized system (4.1)–(4.2) we use the difference notation
and define a staggered scheme, where first \(y^{k-1}_{\varepsilon \tau }\) is updated to \(y^{k}_{\varepsilon \tau }\) while keeping \(\theta ^{k-1}_{\varepsilon \tau }\) fixed, and then \(\theta \) is updated implicitly by updating \(w^{k-1}_{\varepsilon \tau } \) to 
. More precisely, in the domain \(\varOmega \) we ask for
together with the discrete variant of the boundary conditions (4.2) in the form
The main advantage is that the boundary-value problem (4.3a), (4.4a), and (4.4b) for \(y^k_{\varepsilon \tau } \) is the Euler–Lagrange equation of a functional, so that solutions can be obtained by solving the global minimization problem
where \({\mathcal {R}}\) is from (2.18e) and where \(\langle \ell ^k_\tau , y\rangle =\int _\varOmega g^k_\tau {\cdot } y\,\mathrm {d}x + \int _{{\varGamma }_{\textsc {N}}} f^k_\tau {\cdot } y \,\mathrm {d}S\). Clearly, the Euler–Lagrange equation may have more solutions, however for deriving suitable a priori bounds, we will exploit the minimizing properties.
Similarly, the boundary value problem (4.3b) and (4.4c) for \(\theta ^k_{\varepsilon \tau }\), where \(y^{k-1}_{\varepsilon \tau }\) and \( y^k_{\varepsilon \tau }\) are given, has a variational structure. For this, we define the functions \(\phi _\mathrm {C}^{}(F,\theta ):=\int _0^\theta \phi (F,{\widehat{\theta }})\,\mathrm {d}{\widehat{\theta }}\) and \(W(F,\theta )=2\phi _\mathrm {C}^{}(F,\theta ) - \theta \phi (F,\theta )\) to obtain the relation
With 
we see that \(W(F,\cdot )\) is uniformly convex by assumption (2.30c). Thus, we obtain solutions \(\theta ^k_{\varepsilon \tau }\) of (4.3b) and (4.4c) via the minimization problem
We emphasize that this staggered scheme is constructed in a very specific way by taking \(\theta =\theta ^{k-1}_{\varepsilon \tau }\) from the previous time step in the mechanics problem for \(y^k_{\varepsilon \tau }\), see (4.5). For the construction of \(\theta =\theta ^k_{\varepsilon \tau }\) from the heat equation we have to use sometimes the explicit (backward) approximations \(\theta ^{k-1}_{\varepsilon \tau } \) and sometimes the implicit (forward) approximation \(\theta ^k_{\varepsilon \tau }\). Clearly, the former is simpler and it is used in the heat conduction tensor \(\mathcal {K}( \nabla y_{\varepsilon \tau }^{k-1}, \theta _{\varepsilon \tau }^{k-1})\) and in the heat production \(\xi ^\text {reg}_\varepsilon \). It is tempting to use the explicit choice \(\theta ^{k-1}_{\varepsilon \tau }\) also in the thermo-mechanical coupling term \(\partial _F\phi (\nabla y^{k}_{\varepsilon \tau } ,\theta ){:}\nabla \varvec{\delta }_{\!\tau }y^k_\varepsilon \) [= the last term in (4.3b)] as it would simplify the energy balance, see Remark 6.1. However, as this term does not have a sign, we would not be able to guarantee positivity of \(\theta ^k_{\varepsilon \tau }\). Thus we are forced to use the more involved implicit term \(\theta \mapsto \partial _F\phi _\mathrm {C}^{}(\nabla y^{k}_\varepsilon ,\theta ) {:} \nabla \varvec{\delta }_{\!\tau }y^k_\varepsilon \) in (4.7) instead of the simpler, linear choice \(\theta \mapsto \theta \partial _F \phi (\nabla y^{k}_{\varepsilon \tau }, \theta ^{k-1}_{\varepsilon \tau } ){:} \nabla \varvec{\delta }_{\!\tau }y^k_\varepsilon \). This choice may introduce nonconvexity, so that \(\theta ^k_{\varepsilon \tau }\) may not be unique.
The next result states that we can obtain solutions \((y^k_{\varepsilon \tau },\theta ^k_{\varepsilon \tau })\) of (4.3)–(4.4) by solving the minimization problems (4.5) and (4.7), alternatingly. For notational simplicity we have written the minimization problem (4.7) for \(\theta \) with the constraint \(\theta \geqq 0\), however, for establishing the Euler–Lagrange (4.3b) and (4.4c) we need to show that non-negativity of \(\theta \) comes even without imposing the constraint. This will be achieved by minimization over \(\theta \in H^1(\varOmega )\) after extending all functionals suitably for \(\theta <0\).
Proposition 4.1
(Time-discretized solutions via minimization). Let the assumptions in (2.30) be satisfied. For \(N\in \mathbb {N}\) set \(\tau =T/N\) and \( (y^0_{\varepsilon \tau }, \theta ^0_{\varepsilon \tau } ) = (y_0, \theta _{0,\varepsilon } ) \) as in (4.2d) and 
. Then, for \(k=1,\ldots ,N\) we can iteratively find \((y^k_{\varepsilon \tau },\theta ^k_{\varepsilon \tau })\in {\mathcal {Y}}_\mathrm {id}\times H^1_+(\varOmega )\) by solving first the incremental global minimization problem (4.5) and then (4.7). The global minimizers satisfy the time-discretized problem (4.3)–(4.4) in the weak sense and \(\theta ^k_{\varepsilon \tau }\geqq 0\) almost everywhere on \(\varOmega \).
Proof
Mechanical step: We first show that the minimization problem in (4.5) has a solution for any \(\theta ^{k-1}_{\varepsilon \tau }\in H^1(\varOmega )\) with \(\theta ^{k-1}_{\varepsilon \tau } \geqq 0\). We cannot rely on that \(\phi \) is bounded from below, cf. Example 2.4, but we can formally add an x-dependent constant \(-\phi (F_{k-1},\theta _{k-1})\) to the integrand in (4.5). By (2.30c), \(\phi (F,\theta _{\varepsilon \tau }^{k-1})-\phi (F_{\varepsilon \tau }^{k-1},\theta _{\varepsilon \tau }^{k-1})\geqq -K_{\varepsilon \tau }^{k-1}|F|^{s/2+1}\) where the constant \(K_{\varepsilon \tau }^{k-1}\) depends on \(\Vert F_{\varepsilon \tau }^{k-1}\Vert _{L^\infty (\varOmega ;\mathbb {R}^{d\times d})}\) and on K from (2.30c). Since \(s>2\) is assumed, this possible decay is however dominated by the s-growth of \(\varphi \), cf. (2.30a).
Thus, such formally modified functional in the minimization problem (4.5) is coercive on \({\mathcal {Y}}_\mathrm {id}\subset W^{2,p}(\varOmega ;\mathbb {R}^d)\). By lower semicontinuity in \( W^{2,p}(\varOmega ;\mathbb {R}^d)\) we obtain the desired minimizer \(y^k_{\varepsilon \tau } \in {\mathcal {Y}}_\mathrm {id}\) with \({\mathcal {M}}(y^k_{\varepsilon \tau })<\infty \). Hence, Theorem 3.1 shows that the minimizer satisfies \(\det \nabla y(x) \geqq \delta >0\). As in Proposition 3.2 we conclude that \(y^k_{\varepsilon \tau }\) satisfies the Euler–Lagrange equation
but this gives exactly (4.3a), (4.4a), and (4.4b).
Energy step: We now assume that \(\theta ^{k-1}_{\varepsilon \tau }\in H^1(\varOmega )\) and \(y^{k-1}_{\varepsilon \tau }, y^k_{\varepsilon \tau }\in {\mathcal {Y}}_\mathrm {id}\) are given with \(\theta ^{k-1}_{\varepsilon \tau } \geqq 0\) and \({\mathcal {M}}(y^{k-1}_{\varepsilon \tau }), \, {\mathcal {M}}(y^{k}_{\varepsilon \tau }) < \infty \). With this, we show that a variant of the minimization problem (4.7) has a minimizer \(\theta ^k_{\varepsilon \tau }\). For this, we extend the function \(\phi \), which satisfies \(\phi (F,0)=0\) by assumption (2.15), continuously by \(\phi (F,\theta )=0\) whenever \( \theta < 0 \). As the functions 
, \(\phi _\mathrm {C}^{}\), and W are defined through \(\phi \), they all extend continuously differentiable for \(\theta <0\) to the constant value 0. Thus, the integrands in (4.7) are defined for all \(\theta \in \mathbb {R}\) and we can minimize over \(\theta \in H^1(\varOmega )\), that is without the constraint \(\theta \geqq 0\).
Clearly, the extended functional is weakly lower semicontinuous on \(H^1(\varOmega )\) because of \({\mathcal {K}} \geqq 0\). To show coercivity of the functional, we use that \({\mathcal {M}}(y^{k-1}_{\varepsilon \tau })<\infty \) implies \( \nabla y^{k-1}_{\varepsilon \tau } \in L^\infty \) and \(\det \nabla y^{k-1}_{\varepsilon \tau }(x) \geqq \delta >0\). Hence, \({\mathcal {K}}\) given in (2.24) satisfies \(\nabla \theta \cdot {\mathcal {K}}(\nabla y^{k-1}_{\varepsilon \tau }, \theta ^{k-1}_{\varepsilon \tau }) \nabla \theta \geqq \alpha _*|\nabla \theta |^2\) for some \(\alpha _*>0\). Together with the boundary integral, where \(\kappa >0\) due to (2.30g), we have two terms that generate a lower bound \(c_0\Vert \theta \Vert _{H^1(\varOmega )}^2 -C\).
For the remaining term we observe that \(W(F,\theta )\geqq 0\) by construction, while \(\frac{1}{\tau }w^{k-1}_{\varepsilon \tau } \) and \(\xi ^\text {reg}_\varepsilon \) are given functions in \(L^2(\varOmega )\). Finally, for the last bulk term involving \(\partial _F \phi _\mathrm {C}^{}\) we use (2.30b) giving \(|\partial _F \phi (F,\theta )|\leqq K(1+|F|^{s/2})\) and hence, because of \(\nabla y^k_{\varepsilon \tau } \in L^\infty (\varOmega ; \mathbb {R}^{d \times d}) \), we have
Together with \(\varvec{\delta }_{\!\tau }\nabla y^k_{\varepsilon } \in L^2(\varOmega ;\mathbb {R}^{d\times d})\) we can show that all remaining terms can be estimated from below by \(-C\Vert \theta \Vert _{L^2(\varOmega )}\).
In summary, we conclude that the extended functional in (4.7) is weakly lower semicontinuous and coercive. Hence, a global minimizer \(\theta _*\) exists and moreover these minimizers solve the associated Euler–Lagrange equation as 
and \(\partial _\theta \phi _\mathrm {C}^{} (F,\theta ) = \phi (F,\theta )\) depend continuously on \( \theta \).
To show that all global minimizers are non-negative we test the Euler–Lagrange equation by the negative part \(\theta _*^-:=\min \{\theta _*,0\}\) of \(\theta _*\), which is still an \(H^1\) function:
In the first estimate we have used that 
, \(\xi ^\text {reg}_\varepsilon \geqq 0\), and \(\theta ^k_{\flat ,\varepsilon ,\tau }\geqq 0\) which gives the non-negativity of \(p_2\), \(p_4\), and \(p_7\), while the first and fifth term vanish identically since for \(\theta _*>0\) we have \(\theta _*^-=0\) while for \(\theta _*<0\) we have 
and \(\partial _F\phi (F,\theta _*)=0\) (here we crucially use the implicit structure). Thus, we conclude that \(\theta _*^-=0\), which is equivalent to \(\theta _*\geqq 0\).
Thus, choosing \(\theta ^k_{\varepsilon \tau }=\theta _*\) for any global minimizer of the extended functional we see that it is also a global minimizer of (4.7) and that the Euler–Lagrange equations hold. \(\quad \square \)
Considering discrete approximations \(\big (y_{\varepsilon \tau }^k\big )_{k=0,\ldots ,T/\tau }\), we introduce a notation for the piecewise-constant and the piecewise affine interpolants, defined respectively by
The notations \(\theta _{\varepsilon \tau }\), \({\overline{\theta }}_{\varepsilon \tau }\), and \({\underline{\theta }}_{\varepsilon \tau }\) or \(w_{\varepsilon \tau }\) have analogous meanings. However, with \({\overline{g}}_{\tau }(t)\) we refer to the locally averaged loadings \( \overline{g}_\tau (t)= g_\tau ^k\) for \(t\in {]k\tau {-}\tau , k\tau ]}\) (cf. (4.3a)), and similarly for \(\overline{f}_\tau \), \(\overline{\ell }_\tau \) and \(\overline{\theta }_{\flat ,\varepsilon ,\tau }\).
The next result provides the basic energy estimates where we will crucially use the carefully chosen semi-implicit scheme defined through the staggered minimization problems (4.5) and (4.7). Here also we will essentially rely on the regularizing viscous term \(\varepsilon \Delta \dot{y}\), as the bounds provided by \({\mathcal {R}}\) cannot be used because of the missing a priori bound for \(y^k_{\varepsilon \tau }\) in \(W^{2,p}(\varOmega ;\mathbb {R}^d)\). Moreover, we will exploit the fact that we have global minimizers in (4.5) rather than arbitrary solutions of the Euler–Lagrange equations (4.3a). This latter argument works because we have neglected inertial terms in the momentum balance (2.27a) and hence in (4.3a). We refer to [26] for cases where inertial effects are treated, but in the isothermal case.
Recalling the notation \(I=[0,T]\), we formulate our first result.
Proposition 4.2
(First a-priori estimates). Let (2.30) be satisfied, then for all \(\varepsilon >0\) there exists \(K_\varepsilon >0\) such that the following holds. For \(\tau < 1/K_\varepsilon \) the interpolants constructed from the discrete solutions \((y_{\varepsilon \tau }^k,\theta _{\varepsilon \tau }^k) \in W^{2,p}(\varOmega ;\mathbb {R}^d) \times H^1(\varOmega )\), \(k=1,\ldots ,T/\tau \), obtained in Proposition 4.1 satisfy the following estimates:
We emphasize that we did not make any smoothness assumptions for \(\theta _0\), hence the regularized initial values \(\theta ^0_{\varepsilon \tau }:=\theta _{0,\varepsilon }\) and 
are not smooth. This explains, why we have to use the left-continuous interpolants in (4.9c) and (4.9d) and why \(L^2([\tau ,T];H^1(\varOmega ))\) used in (4.9e,f) avoids the interval \([0,\tau ]\) on which the approximate solution may fall out of \(H^1(\varOmega )\) due to the initial condition \(\theta _{0,\varepsilon }\in L^\infty (\varOmega )\), cf. (2.30i) and (4.2d).
Proof
As \(y^k_{\varepsilon \tau }\) is a global minimizer, we can insert \(y=y^{k-1}_{\varepsilon \tau }\) as testfunction in (4.5) to obtain the estimate (recall \(\varvec{\delta }_{\!\tau }y^k_\varepsilon = \frac{1}{\tau }(y^k_{\varepsilon \tau }{-}y^{k-1}_{\varepsilon \tau })\))
The proof will be divided into three steps.
Step 1: Uniform energy bound. Using the decomposition \(\varPsi (y,\theta )={\mathcal {M}}(y)+\varPhi _\mathrm {cpl}(y,\theta )\), see (2.18b), we can write (4.10) equivalently as
To estimate the last term use the assumption (2.30b) on \(|\partial _F\phi (F,\theta )|\) as follows
where \(\rho >0\) is arbitrary. Choosing \(\rho =\varepsilon /(4\tau )\) and \(F_j=\nabla y^{k+j-2}_{\varepsilon \tau }\) we can insert this into the estimate (4.11). Moreover we can use \({\mathcal {R}}\geqq 0\) and \(\langle \ell ^k_\tau , \varvec{\delta }_{\!\tau }y^k_\varepsilon \rangle \leqq \Vert \ell ^k_\tau \Vert _{H^{-1}} \Vert \varvec{\delta }_{\!\tau }y^k_\varepsilon \Vert _{H^1} \leqq c_\mathrm {P}^{}\Vert \ell ^k_\tau \Vert _{H^{-1}}\Vert \nabla \varvec{\delta }_{\!\tau }y^k_\varepsilon \Vert _{L^2} \) as \(\varvec{\delta }_{\!\tau }y^k_\varepsilon \in {\mathcal {Y}}_0\). This leads to
Using the coercivity assumption (2.30b) for \(\phi \), the second-last term can be estimated by \({\mathcal {M}}\) again and setting \(m_k:= {\mathcal {M}}(y^k_{\varepsilon \tau })\) we obtain the recursive estimate
with \({\widetilde{c}}_\varepsilon =2{\cdot }3^s K^2/\varepsilon \) and \(\overline{c}_\varepsilon = 2 c_\mathrm {P}^2/\varepsilon \). In a first step we neglect the last term on the left-hand side and obtain
We now restrict \(\tau >0\) via \(\tau <1/(2{\widetilde{c}}_\varepsilon )\) by choosing \(K_\varepsilon \geqq 2{\widetilde{c}}_\varepsilon \), so we can iterate the above estimate. With (2.30h) we have \(m_0:=\varPsi (y_0,\theta _0)<\infty \) and a simple induction yields the discrete Gronwall-type estimate (with \(Q_\varepsilon = (1{+}\tau {\widetilde{c}}_\varepsilon )/(1{-}\tau {\widetilde{c}}_\varepsilon )\))
Using Theorem 3.1 we obtain the desired uniform upper bound in (4.9a) for the interpolant \(y_{\varepsilon \tau }:I=[0,T]\rightarrow {\mathcal {Y}}_\mathrm {id}\) in \(L^\infty \big (I; W^{2,p} (\varOmega ; \mathbb {R}^d)\big )\), as well as the lower bound (4.9b) for the determinant.
Step 2: Dissipation bound. We return to (4.13) and add all estimates from \(k=1\) to \(N_\tau :=T/\tau \in \mathbb {N}\) to obtain
This provides the uniform bound for \(y_{\varepsilon \tau }\) in \(H^1(I;H^1(\varOmega ;\mathbb {R}^d))\), and (4.9a) is established.
Step 3: Temperature bounds. Testing the Euler–Lagrange equations (4.3b) and (4.4c) by \(w_{\varepsilon \tau }^k\) yields the identity
Recalling 
we obtain the chain rule
Moreover, we have the elementary estimate \( \frac{1}{\tau }(w^k_{\varepsilon \tau }{-}w^{k-1}_{\varepsilon \tau }) w^k_{\varepsilon \tau } \leqq \frac{1}{2\tau }\big ( (w^k_{\varepsilon \tau })^2-(w^{k-1}_{\varepsilon \tau })^2\big )\), and 
by the definition of 
. Using additionally \(c_\mathrm {v}(F,\theta )=-\theta \partial _{\theta \theta }^2 \phi (F,\theta ) \geqq \widehat{\varepsilon }\), see (2.30c), the above identity (4.15) leads to
Using the uniform bounds for \(\nabla y_{\varepsilon \tau }\) and \(\det \nabla y_{\varepsilon \tau }\) from Step 1, the assumptions on \({\mathbb {K}}\) in (2.30f), as well as formula (2.24) we find a \(\varkappa _\varepsilon \) such that
Moreover, using 
, the assumptions (2.30b) and (2.30c) together with the uniform \(L^\infty \) bound for \(\nabla y_{\varepsilon \tau }\) we find 
. Realizing also that we have \(\nabla ^2y_{\varepsilon \tau }^k\) already estimated in \(L^p(\varOmega ;\mathbb {R}^{d\times d\times d})\) with \(p\geqq 2\) we obtain \(\Vert b^k_{\varepsilon \tau }\Vert _{L^2} \leqq \overline{C}_\varepsilon \). For the right-hand side \(h^k_{\varepsilon \tau }\) of (4.15) we have
where we again used the \(L^\infty \) bounds for \(\nabla y^k_{\varepsilon \tau }\). Finally, by definition we have \(\theta _{\flat ,\varepsilon } \in [0,1/\varepsilon ]\), and (2.31) allows us to estimate w by \(\theta \), which yields the boundary estimate
Based on the above estimates and introducing the abbreviations
we can estimate the right-hand side in (4.17) via
where \(\alpha >0\) is arbitrary. Estimating the last term on the left-hand side in (4.17) from below by \( \widehat{\varepsilon }\,\Theta _k^2/\varkappa _{\varepsilon }\) we may choose \(\alpha = \widehat{\varepsilon }/(2\varkappa _{\varepsilon }\overline{c}_\varepsilon )\). After multiplying (4.17) by \(2\tau \) we obtain
Arguing as in Steps 1 and 2 for (4.13) and using \(\gamma _0^2 = \int _\varOmega w^0_{\varepsilon \tau }\,\mathrm {d}x \leqq K^2\int _\varOmega \theta _{0,\varepsilon }^2 \,\mathrm {d}x \leqq K^2|\varOmega |/\varepsilon ^2 < \infty \) [cf. (4.2d)] the left-continuous interpolants \(\overline{\theta }_{\varepsilon \tau }\) and \(\overline{w}_{\varepsilon \tau }\) satisfy the a priori estimates (recalling 
from (2.31))
Thus, we find (4.9c) for \(\overline{\theta }_{\varepsilon \tau }\), and estimate (4.9d) follows by using (4.16) once again.
The uniform estimate for the piecewise affine interpolant \(w_{\varepsilon \tau }\) in the spaces \( C(I;L^2(\varOmega )) \cap L^2( [\tau ,T]; H^1(\varOmega ) ) \) follows from the previous estimates for \(\overline{w}_{\varepsilon \tau }\). Finally, we note that the time derivative of the interpolant \(w_{\varepsilon \tau }\) is equal to \(\varvec{\delta }_{\!\tau }w^k_\varepsilon \) on the intervals \({](k{-}1)\tau ,k\tau [}\). We now use the Euler–Lagrange equations (4.3b) and (4.4c), which provides for \(\varvec{\delta }_{\!\tau }w^k_\varepsilon = \frac{1}{\tau }(w^k_\varepsilon {-} w^{k-1}_\varepsilon ) \) the estimate
Squaring and summation over \(k=1,\dots , N_\tau \) gives the remaining uniform bound in (4.9e) for \(\dot{w}_{\varepsilon \tau }\) in \(L^2 \big ( I; H^1(\varOmega )^* \big ) \). \(\quad \square \)
Remark 4.3
(Full space-time discretization). To be useful for an implementable algorithm, our time discretization should be combined with a spatial discretization. A suitable space discretization itself (leading to the Faedo–Galerkin method) was introduced in [26, Sect. 9.3] even without requiring the \(\varepsilon \)-regularization (4.1). This suggests that the space-time discretization might work with \(\varepsilon =0\) under a suitable stability criterion that the time step is sufficiently small with respect to the mesh size used for the space discretization. Or, vice versa, our analysis suggests that the \(\varepsilon \)-regularization makes the stability criterion obsolete, assuming that both time step and mesh size are sufficiently small with respect to \(\varepsilon \). However, our focus does not lie in such numerical aspects, and we leave these questions for further research.
5 The Limit \({\tau \rightarrow 0}\) in the Regularized Problem
Using the above a priori estimates for the interpolants we will be able to extract convergent subsequences. First we will observe that the three different types of interpolants have to converge to the same limit. Next we want to pass to the limit in the discretized weak forms of the momentum balance and the heat equation. While most terms can be handled by compactness arguments or weak-convergence methods, there is one term that needs special attention, namely the heat-source term \(\xi ^\mathrm {reg}_\varepsilon \) that is quadratic in \(\nabla \dot{y}_\varepsilon \). Thus, it will be a crucial step to show strong convergence of \(\dot{y}_{\varepsilon \tau }\) in \(L^2(I; H^1(\varOmega ))\), which can be done by passing to the limit in a suitable discretized version of the mechanical energy balance (2.20). In this argument we will use the \(\Lambda \)-convexity derived in Proposition 3.2 to relate the mechanical energies \({\mathcal {M}}(y^{k-1}_{\varepsilon \tau }) \) and \({\mathcal {M}}(y^k_{\varepsilon \tau })\).
With the definition (4.8) for the three types of interpolants, we see that the following discretized version (5.1) of the momentum balance and heat equations (4.1) and (4.2) holds for the discrete solutions constructed in Proposition 4.1:
to hold on \(Q=[0,T]\times \varOmega \), while the regularized boundary conditions (4.4) read
Here it is essential that we have to use all three types of interpolants, for example \(\overline{y}_{\varepsilon \tau },\ \underline{y}_{\varepsilon \tau }\), and \(y_{\varepsilon \tau }\). In particular, we emphasize that \(t\mapsto w_{\varepsilon \tau }(t)\) is the piecewise affine interpolant of \(\{w^k_{\varepsilon \tau }\}_{k=0,\ldots ,N_\tau }\), which does not coincide with 
except at the nodal points \(t=k\tau \).
Proposition 5.1
(Convergence for \(\tau \rightarrow 0)\). Let (2.30) hold, and let \(\varepsilon >0\) be fixed. Then, considering a sequence of time steps \(\tau \rightarrow 0\), there are limit functions \(y_\varepsilon \) and \(\theta _\varepsilon \) and a subsequence (not relabeled) such that
Moreover, any couple \((y_\varepsilon ,\theta _\varepsilon )\) obtained by this way is a weak solution to the regularized initial-boundary-value problem (4.1)–(4.2) in the sense of Definition 2.1 written for \((y_\varepsilon ,\theta _\varepsilon )\) with \(\varepsilon \nabla \theta _\varepsilon {:}\,\nabla z\) added in the first integral in (2.27a). Moreover, it satisfies the corresponding mechanical energy-dissipation balance, see (5.9) below.
Proof
The proof consists of five steps.
Step 1: Extraction of convergent subsequences. As \(\varepsilon >0\) is still fixed, we can exploit the a priori estimates obtained in Proposition 4.2, namely (4.9a) and (4.9f). By Banach’s selection principle, we choose a subsequence and some \((y_\varepsilon ,\theta _\varepsilon )\) such that (5.3) holds. By the Aubin–Lions theorem combined with an interpolation, as \(p>d\), we also have
Indeed, for the first result we use the continuous embedding \(W^{1,p}(\varOmega ) \subset C^\alpha ( \overline{\varOmega })\) with \(\alpha =1-d/p\in {]0,1[}\) and thus \(\Vert \nabla y_{\varepsilon \tau }\Vert _{C^\alpha } \leqq K_0\). Moreover, (4.9a) yields the Hölder estimate
While the first part of (4.9a) yields just \(\Vert \nabla y_{\varepsilon \tau }(t_1)-\nabla y_{\varepsilon \tau }(t_2)\Vert _{W^{1,p}(\varOmega ;\mathbb {R}^{d\times d})} \leqq K_0\). By interpolation, we find \(\beta \in {]0,\alpha [}\) and \(\lambda \in {]0,1[}\) such that we have \(\Vert \cdot \Vert _{C^\beta }\leqq C\Vert \cdot \Vert _{C^\alpha }^{1-\lambda }\Vert \cdot \Vert _{L^2}^\lambda \) and conclude
Thus, the sequence \(\{\nabla y_{\varepsilon \tau }\}\) is uniformly bounded in \(C^\gamma (\overline{Q})\) for \(\gamma =\min \{\beta ,\lambda /2\}\), and uniform convergence follows by the Arzelà–Ascoli theorem.
The convergence (5.4b) follows from (5.3b) by the Aubin–Lions theorem when interpolated with the estimate in \(L^\infty (I;L^2(\varOmega ))\) which is contained in the estimate (4.9e).
Moreover, both convergences in (5.4) hold also for the piecewise constant interpolants because of the estimates \(\Vert \nabla y_{\varepsilon \tau }-\nabla \underline{y}_{\varepsilon \tau } \Vert _{L^\infty (I; L^2(\varOmega ; \mathbb {R}^{d\times d}))}\leqq K\tau ^{1/2}\) (and the same also for \(\nabla {\overline{y}}_{\varepsilon \tau }\)).
Moreover, from \(\Vert w_{\varepsilon \tau }\Vert _{H^1(I;H^1(\varOmega )^*)}\leqq K_\varepsilon \), cf. (4.9e), one can also read the estimate \(\Vert \overline{w}_{\varepsilon \tau }\Vert _{\mathrm{BV}(I;H^1(\varOmega )^*)}\leqq \sqrt{T}K_\varepsilon \) so that \(\overline{w}_{\varepsilon \tau }\) converges (as a selected subsequence) strongly in \(L^s(Q)\) with s from (5.4b) by a generalization of the Aubin–Lions theorem for time-derivatives as measures, cf. [44, Cor. 7.9]. The limit must coincide with \(w_\varepsilon \) because \(\Vert w_{\varepsilon \tau }-\overline{w}_{\varepsilon \tau }\Vert _{L^2(I;H^1(\varOmega )^*)}=3^{-1/2} \tau \Vert \dot{w}_{\varepsilon \tau }\Vert _{L^2(I;H^1(\varOmega )^*)}\geqq 0\).
By (2.31), 
has an inversion which is Lipschitz continuous. Thus, by (4.3c) 
, and we have, beside (5.3b), also
for all \(s\in {[1,\min \{4,2+4/d\} [}\).
Step 2: Convergence in the mechanical equation. Now the convergence in the discretized momentum balance (5.1a) can be done by the above weak convergences (5.3) because \(\sigma _\mathrm {vi}\) is linear in terms of \(\dot{F}\) and by Minty’s trick for the monotone operator induced by \({\mathfrak {h}}_\mathrm {el}={\mathscr {H}}'\). For a reflexive Banach space X and a hemi-continuous, monotone operator \(\mathbf {H}:X\rightarrow X^*\) Minty’s trick means the implication
We apply this for \(\mathbf {H}\) defined by \(\langle \mathbf {H}(y),z\rangle = \int _Q {\mathfrak {h}}_\mathrm {el}(\nabla ^2y(t,x))\!\;\vdots \!\;\nabla ^2 z(t,x)\,\mathrm {d}x \,\mathrm {d}t\), where \(X=W^{2,p}(Q)\). Clearly, \(\mathbf {H}\) is hemi-continuous and monotone. Choosing \(u_\tau =\overline{y}_{\varepsilon \tau }\) the weak equations (5.1a) and (5.2) are interpreted as \(\mathbf {H}(\overline{y}_{\varepsilon \tau })=b_\tau \) with \(b_\tau \) defined via
We obtain \(b_\tau \rightharpoonup b\) with b defined by
because we can pass to the limit \(\tau \) in all four terms separately. For the first term we apply the lower semicontinuity result [21, Thm. 7.5] twice, namely for the integrands \(f_\pm (x,(F,\theta ),G)=\pm \sigma _\mathrm {vi}(F,G,\theta ){:}\nabla z(x)\) which both are convex in G. The limit passage in the second term is simple weak convergence, and the fourth term converges because of \(\overline{\ell }_\tau \rightarrow \ell \) in \(L^2\big (I;H^1_\mathrm {D}(\varOmega )^*\big )\). In the third term we exploit
(see (4.9a) and (4.9b) from Proposition 4.2), such that using (2.30a) and (2.30b) the map \((F,\theta )\mapsto \sigma _\mathrm {el}(F,\theta )=\partial _F\varphi (F)+\partial _F \phi (F,\theta )\) is continuous and bounded on \({\mathbb {F}}(K_\varepsilon )\times \mathbb {R}^+\). Hence, with (5.4) and Lebesgue’s dominated convergence theorem we obtain the desired convergence.
To use Minty’s trick (5.8) we still need to check \(\langle b_\tau , \overline{y}_{\varepsilon \tau }\rangle \rightarrow \langle b,y_\varepsilon \rangle \). However, we have shown above that \(b_\tau \) is bounded (and hence weakly converging to b) in \(L^2\big (I;H^1_\mathrm {D}(\varOmega )^*\big )\) and \( \overline{y}_{\varepsilon \tau } \rightarrow y_\varepsilon \) in \(L^2\big (I;H^1_\mathrm {D}(\varOmega )\big )\) strongly by (5.4a), thus the result follows immediately. Hence, we conclude \(\mathbf {H}(y_\varepsilon )=b\), which is nothing else but the regularized momentum balance (4.1a), (4.2a), and (4.2b).
Step 3: Balance of mechanical energy. For the limit passage in the heat equation we need strong \(L^2\)-convergence of \(\nabla \dot{y}_{\varepsilon \tau }\) due to the viscous dissipation \(\xi ^\mathrm {reg}_\varepsilon (F,\dot{F},\theta )\) that is nonlinear in \(\dot{F}\). The strategy is to use the balance of mechanical energy by rewriting the regularized momentum balance (4.1a), (4.2a), and (4.2b) in the form
with \({\mathcal {M}}\) and \(\varPhi _\mathrm {cpl}\) defined in (2.18). We can now test with \(\dot{y}_\varepsilon \in L^2(I;H^1_\mathrm {D}(\varOmega ))\) and use (after decomposing \({\mathcal {M}}={\mathcal {H}}+\varPhi _\mathrm {el}\), see (2.18)) the chain rule in Proposition 3.6 to obtain the balance of mechanical energy in the form
Indeed, by Proposition 3.2 we know that \({\mathcal {M}}\) satisfies the assumptions of Proposition 3.6 with space \(X=H^1_{{\varGamma }_{\textsc {D}}}(\varOmega ;\mathbb {R}^d)\). Clearly, \(y_\varepsilon \in H^1(I;X)\) and \({\mathcal {M}}(y_\varepsilon (t))\leqq {\widetilde{K}}_\varepsilon \), see (4.14). Moreover, for
we have \(\varXi _{\varepsilon }(t)= \mathrm {D}{\mathcal {M}}(y_{\varepsilon }(t))\) almost everywhere in [0, T] and our a priori estimates provide \(\varXi _{\varepsilon }\in L^2([0,T];H^1_{{\varGamma }_{\textsc {D}}}(\varOmega )^*)\). Thus, (5.9) follows from Proposition 3.6.
Step 4: Strong convergence of strain rates. The next step is now to derive a similar mechanical energy balance for the time-discretized solutions, which is better than the previously used estimate (4.11). Passing to the limit \(\tau \rightarrow 0\) from the latter estimate we would arrive at an estimate like (5.9), but with \(2{\mathcal {R}}\) and \(\varepsilon \) replaced by \({\mathcal {R}}\) and \(\varepsilon /2\), respectively.
To improve the discrete estimate (4.11) used in Proposition 4.2 we can exploit the a priori estimates \({\mathcal {M}}(y^k_{\varepsilon \tau })\leqq K_\varepsilon \), which allow us to use the geodesic \(\Lambda \)-convexity result in Proposition 3.2. Instead of using the minimization property of \(y^k_{\varepsilon \tau }\) in (4.5) we test the Euler–Lagrange equation (4.3a) with boundary conditions (4.4a) and (4.4b) by \(y^k_{\varepsilon \tau }{-}y^{k-1}_{\varepsilon \tau }\) to obtain
where we have the correct factors \(2{\mathcal {R}}\) and \(\varepsilon \). To recover the energy values \({\mathcal {M}}(y^{j}_{\varepsilon \tau })\) we now eliminate the term involving \(\mathrm {D}{\mathcal {M}}\) using the \(\Lambda \)-convexity estimate (3.3) with \(y^{(1)}=y^k_{\varepsilon \tau }\) and \(y^{(2)}=y^{k-1}_{\varepsilon \tau }\), which yields
We now sum this inequality over \(k=1,,\ldots , N_\tau \) and using the interpolants we obtain the integral estimate
Using the convergences in (5.3) and (5.4), it is immediate to see that all the terms on the right-hand side converge to the corresponding terms on the right-hand side in (5.9). Now denote the three terms on the left-hand side by \(I^{(j)}_{\varepsilon \tau }\) and set \(I^{(j)}_\varepsilon = \liminf _{\tau \rightarrow 0^+} I^{(j)}_{\varepsilon \tau }\). Using lower semicontinuity arguments (use [21, Thm. 7.5] once again for \(I^{(2)}_{\varepsilon \tau }\)) we find
Thus, passing to the liminf on the left-hand side and to the limit on the right-hand side in (5.10) and comparing with (5.9) we obtain
Together with (5.11) we conclude that we must have equality in all three cases after “\(\Longrightarrow \)”. However, \(\nabla \dot{y}_{\varepsilon \tau }\rightharpoonup \nabla \dot{y}_\varepsilon \) in \( L^2(Q;\mathbb {R}^{d\times d}) \) and
imply the desired strong convergence \(\nabla \dot{y}_{\varepsilon \tau } \rightarrow \nabla \dot{y}_\varepsilon \) in \( L^2(Q;\mathbb {R}^{d\times d})\).
Step 5: Limit in the heat equation. We first pass to the limit \(\tau \rightarrow 0\) in the constitutive relation (5.1b), namely 
. The left-hand side converges to \(w_\varepsilon \) by (5.7), while the right-hand side converges to 
by the continuity of 
, the bound (2.31) and the convergences (5.4). Thus, 
is established, that is (4.1c) holds.
We write the heat equation (5.1b) with boundary conditions (5.2c) in the weak form
for all \(z \in L^\infty (I;H^1(\varOmega ))\). While we only have the weak convergences \(\dot{w}_{\varepsilon \tau } \rightharpoonup \dot{w}_\varepsilon \) in \(L^2 \big ( I; H^1 (\varOmega )^*\big )\) [see (5.7)] and \(\nabla \overline{\theta }_{\varepsilon \tau } \rightharpoonup \nabla \theta _\varepsilon \) in \(L^2(Q)\) (see (5.3b)), all other functions in (5.12) converge strongly. In particular, using the strong convergences \(\nabla \dot{y}_{\varepsilon \tau } \rightarrow \nabla \dot{y}_\varepsilon \) in \( L^2(Q;\mathbb {R}^{d\times d})\) and \(0\leqq \xi ^\mathrm {reg}_\varepsilon (\nabla \underline{y}_{\varepsilon \tau }, \!\nabla \dot{y}_{\varepsilon \tau },{\underline{\theta }}_{\varepsilon \tau }) \leqq K_\varepsilon \) we obtain
Thus, passing to the limit \(\tau \rightarrow 0\) in (5.12) leads exactly to the weak form to the regularized heat equation (4.1b) with boundary condition (4.2c).
This concludes the proof of Proposition 5.1. \(\quad \square \)
6 Limit Passage \({\varepsilon \rightarrow 0}\)
In this final part of the proof of Theorem 2.2 we have to pass to the limit with the regularization parameter \(\varepsilon \rightarrow 0\). As we are already in the time-continuous setting we are now able to make the formally derived total energy balance (2.21) for \({\mathcal {E}}\) rigorous for all \(\varepsilon >0\). From this we will be able to derive a priori bounds for \((y_\varepsilon , \theta _\varepsilon )\) that are independent of \(\varepsilon \).
Remark 6.1
(Missing discrete estimate for the total energy). The derivation of the total energy balance is achieved by testing the momentum balance by \(\dot{y}\) and the heat equation by the constant function 1. The corresponding step on the time-discrete level would be the test (4.3a) by \(\varvec{\delta }_{\!\tau }y^k\) and (4.3b) by 1. We would be able to use the desirable cancellation of the dissipation, namely \(\xi ^\text {reg}_\varepsilon -\xi \leqq 0\); however for the coupling terms
which arise from (4.3a) and (4.3b) respectively, we do not have any way to estimate the first against the second. Recall that we were forced to use the explicit/forward value \( \theta ^{k}_{\varepsilon \tau }\) to maintain positivity of the temperature.
To exploit the balance of the total energy we have to strengthen the assumption on the loading \(\ell (t)\), that is the functions g, and f, in (2.30g), namely
This implies that \(t \mapsto \ell (t)\) lies in \(W^{1,1}\big (I;H^1_{{\varGamma }_{\textsc {D}}}(\varOmega ;\mathbb {R}^d)^*\big )\), which is what we will only need.
The new \(\varepsilon \)-independent estimates on \(\nabla \dot{y}_\varepsilon \) in \(L^2(Q)\) will be obtained by exploiting Pompe’s generalization of Korn’s inequality (cf. [41]) as prepared in Theorem 3.3 above.
Lemma 6.2
(A-priori estimates for \(y_\varepsilon ).\) Let the assumptions in (2.30) and (6.1) hold. Then there exists a constant K such that for all \(\varepsilon \in {]0,1[}\) and all weak solutions \((y_\varepsilon ,\theta _\varepsilon )\) of the regularized problem (4.1)–(4.2) obtained in Proposition 5.1 we have
\(\det (\nabla y_{\varepsilon })>0\) on Q and the following estimates hold with K independent of \(\varepsilon >0{:}\)
Proof
We proceed in two steps that are close to estimates we have done in the time-discrete setting.
Step 1: Estimate for\({\mathcal {E}}(y_\varepsilon ,\theta _\varepsilon )\) Using the derived regularity for the solution \((y_\varepsilon ,\theta _\varepsilon )\) we see that a suitable variant of the total energy balance (2.21) holds. To be specific, we start from (5.9), which is also valid for arbitrary \(t\in {]0,T]} \) in place of T, and add the time-integrated version of (4.1b) tested with the constant function \(z\equiv 1\). Using \({\mathcal {E}}={\mathcal {M}}+{\mathcal {W}}\) with \({\mathcal {W}}(y_\varepsilon ,\theta _\varepsilon )=\int _\varOmega w_\varepsilon \,\mathrm {d}x \) we find
The important point here is the cancellation of the term \(\partial _F\phi {:}\,\nabla \dot{y}_\varepsilon \) and that the difference of the dissipation integrals has a sign.
Defining the auxiliary variable \(E_\varepsilon (t):= {\mathcal {E}}(y_\varepsilon (t),\theta _\varepsilon (t)) - \langle \ell (t),y_\varepsilon (t)\rangle \) and using \(0\leqq \theta ^\varepsilon _\flat \leqq \theta _\flat \) and \(\theta _\varepsilon \geqq 0\) gives
where we have integrated by parts the power of the external loadings, which was possible by the strengthened assumption (6.1).
With \({\mathcal {E}}\geqq {\mathcal {M}}\geqq {\mathcal {H}}\) and the coercivity of \({\mathcal {H}}\) we have \(\Vert y\Vert _{H^1} \leqq c_1 + c_2 {\mathcal {E}}(y,\theta )\) and obtain
and \(a,b\in L^1(0,T)\), which follows from (6.1) for \(\ell \) and (2.30i) for \(\theta _\flat \). With \(B(t)=\int _0^t b(s) \,\mathrm {d}s \) and \(A(t) = \int _0^t a(s) \,\mathrm {d}s\) the Gronwall estimate yields the a priori estimate
where we used \({\mathcal {E}}_\varepsilon (0)={\mathcal {E}}(y_\varepsilon (0),\theta _\varepsilon (0)) \leqq {\mathcal {E}}(y_0,\theta _0)-\langle \ell (0), y_0\rangle =:E^0<\infty \) by (2.30h), (2.30i), and (2.31). This immediately implies
Hence, (6.2c) is established, whereas (6.2a) and (6.2b) follow by applying Theorem 3.1.
Step 2: Estimate for the strain rate\(\nabla \dot{y}_\varepsilon \) We return to the mechanical energy balance (5.9) on the interval \(I=[0,T]\). We recall that the dissipation function \(\xi (F,\dot{F},\theta )\) is assumed to control the symmetric part of \(F^\top \dot{F}\) only, namely
Using our a priori bounds on \({\mathcal {M}}(y_\varepsilon (t))\), we can apply the generalized Korn inequality prepared in Corollary 3.4 with \(y=y_\varepsilon (t,\cdot )\) and \(v= \dot{y}_\varepsilon (t) \in H^1_{{\varGamma }_{\textsc {D}}}(\varOmega ; \mathbb {R}^d)\) to obtain
where we used \(|\partial _F \phi (F,\theta )| \leqq |C(1{+}|F|)^s\) and \(|\nabla y_\varepsilon (t,x)|\leqq K\), which follows from (6.2a). Using this, (6.2d) and (6.2e) follow immediately. \(\quad \square \)
For the deformation \(y_\varepsilon \) we have all the estimates we need for passing to the limit, but we still need good a priori estimates for the temperature. Here the problem arises that the heating generated by through the viscous dissipation \(\xi (\nabla y_\varepsilon ,\nabla \dot{y}_\varepsilon ,\theta _\varepsilon )\) is only bounded in \(L^1(Q)\). Thus, for obtaining improved estimates, we have to invoke special test functions developed by Boccardo and Gallouët [11] for parabolic equations with measure-valued right-hand sides.
Proposition 6.3
(A priori estimates for \(\theta _\varepsilon \) and \(w_\varepsilon ).\) Under the conditions of Lemma 6.2, also the following estimates hold:
Proof
We follow the recipe in [11] in the simplified variant of [22], see also [33]. For \(\eta \in {]0,1[}\) we define the function \(\chi _\eta {:}\,\mathbb {R}^+\rightarrow \mathbb {R}^+\) via
Clearly, \(\chi _\eta \) satisfies \(\min \{0,\frac{w}{2} - C_\eta \} \leqq \chi _\eta (w) \leqq w\) and \(\chi ''_\eta (w)= \dfrac{\eta }{(1{+}w)^{1+\eta }}>0\).
Now testing (4.1b) with the test function \(z= \chi '_\eta \circ w_\varepsilon \) amounts to applying the chain rule in Proposition 3.5 to the convex functional \({\mathcal {J}}(w)=\int _\varOmega \chi _\eta (w(x)) \,\mathrm {d}x\) on the space \(X=H^1(\varOmega )^*\). Indeed, from (5.3) and 
we have \(w_\varepsilon \in L^2 (I; H^1(\varOmega )) \cap H^1(I;H^1(\varOmega )^*)) \), and the chain rule gives the first identity in the following calculation:
Integration over \(t\in I=[0,T]\) and using \(\chi '_\eta (w) \in [0,1]\) and \(\Vert \nabla y_\varepsilon \Vert _{L^\infty (Q)} \leqq K_\infty \) yield
where we used (2.30h), (2.30i), (6.2d), and (6.2e).
From this, we derive an a priori bound on \(\nabla w_\varepsilon \) by setting \(\widetilde{{\mathcal {K}}}_\varepsilon ={\mathcal {K}}(\nabla y_\varepsilon ,\theta _\varepsilon )\) and estimate it as in (4.18) (see Step 3 of the proof of Proposition 4.2) by
where \(\varkappa \) is now independent of \(\varepsilon \) because of the \(\varepsilon \)-independent bound in (6.2a) and (6.2b). Moreover, \(\nabla w_\varepsilon \) and \(\nabla \theta _\varepsilon \) are related by
With 
and 
we obtain
Subtracting \(\frac{1}{2K\varkappa } |\nabla w_\varepsilon |^2\), multiplying by \(\chi ''(w_\varepsilon )\in [0,1]\), and integrating over Q we can employ (6.4) and arrive at
where the last integrand is bounded by (6.2a) using \(p\geqq 2\).
For \(r\in {[1,2[}\) we set \(p=2/(2{-}r)\), \(p'=2/r\), and \(q=(1{+}\eta ) r/2\) and employ Hölder’s estimate to obtain
where crucially relied on \(p'=2/r\), \(\chi ''(w)=\eta /(1{+}w)^{1+\eta }\), and the previous estimate. Using the a priori estimate \(\Vert 1{+}w_\varepsilon \Vert _{L^\infty (I;L^1(\varOmega ))} \leqq T|\varOmega | + K=:K_1\) from (4.9f) we can now use the anisotropic Gagliardo–Nirenberg interpolation (see for example [33, Lem. 4.2]) giving
For inserting this into (6.6) we need \(qp \leqq r/\lambda \) which gives the restriction \(r\leqq 2-(1{+}\eta ) \lambda \).
Thus, for all \(r\in {[1,(d{+}2)/(d{+}1)[}\) we find an \(\eta =\eta _r \in {]0,1[}\) such that the above estimates give
and \(q_r\lambda< q_r=(1{+}\eta _r)r/2 < r\) provide \(\Vert \nabla w_\varepsilon \Vert _{L^r(Q)} \leqq K_r\). Using (6.5) and 
we easily find \(\Vert \nabla \theta _\varepsilon \Vert _{L^r(Q)} \leqq K_r\) and (6.3b) is established.
Applying Gagliardo–Nirenberg interpolation once again gives assertion (6.3a).
Eventually, the a priori estimate (6.3c) is obtained estimating all other terms in (4.1b), when realizing that always \(H^{(d+3)/2}(\varOmega )\subset W^{1,\infty }(\varOmega )\). \(\quad \square \)
We are now in the position to pass to the limit \(\varepsilon \rightarrow 0\) in the regularized system (4.1)–(4.2), and thus conclude the proof of our main existence result presented in Theorem 2.2. The approach is close to the convergence result presented in Proposition 5.1: first we extract converging subsequences and then pass to the limit in the mechanical momentum balance. This also provides the necessary strong convergence of the strain rates that is needed to eventually pass to the limit in the heat equation.
Proposition 6.4
(Convergence for \(\varepsilon \rightarrow 0).\) Let again (2.30) and (6.1) hold. Then, considering the limit \(\varepsilon \rightarrow 0\), there are functions y and \(\theta \) and a subsequence \((y_\varepsilon ,\theta _\varepsilon )\) (not relabeled) of weak solutions to the regularized system (4.1)–(4.2) obtained in Proposition 5.1 such that it holds that
Moreover, every couple \((y,\theta )\) obtained in such a way is a weak solution, according Definition 2.1, of the boundary-value problem (2.13)–(2.14) satisfying the initial conditions (2.26).
Proof
The proof follows the lines of the proof of Proposition 5.1, so we do not repeat all details of the arguments.
Step 1: Extraction of converging subsequences. Using the a priori estimates (6.2) and (6.3), Banach’s selection principle allows us to choose a subsequence and some \((y,\theta )\) such that (6.7) holds. By the Aubin–Lions’ theorem interpolated with the estimates in (4.9a) and (4.9c), we also have
The proof of (6.8a) is similar to (5.4a). For (6.8b) we proceed as for (5.4b) by using the estimates on \(w_\varepsilon \) given in (6.3). Using the relation 
we also obtain the strong convergence (6.8c).
Step 2: Convergence in the mechanical equation. The limit passage in the momentum balance (4.1a)–(4.2) works as before, again using the Minty trick (5.8). Of course, the additional regularizing viscosity term \(\varepsilon \nabla \dot{y}_\varepsilon \) vanishes because of our a priori bound (6.2d):
Step 3: Balance of mechanical energy. As in the proof of Proposition 5.1 we derive from the property that the limit couple \((y,\theta )\) solves the mechanical equation that the following mechanical energy relation holds (again exploiting the chain rule in Proposition 3.6):
Step 4: Strong convergence of the symmetric strain rates. We can pass to the limit \(\varepsilon \rightarrow 0\) in the mechanical energy relation (5.9). Comparing the result with (6.9) we obtain
To conclude strong convergence we use the special form (2.10), namely \(\xi (F,\dot{F},\theta )= 2{\widehat{\zeta }}(F^\top F, F^\top \dot{F} {+}\dot{F}^\top F,\theta )\). From the pointwise convergence \(\theta _\varepsilon \rightarrow \theta \), the uniform convergence \(F_\varepsilon :=\nabla y_\varepsilon \rightarrow F=\nabla y\), and the weak convergence \(\dot{F}_\varepsilon :=\nabla \dot{y}_\varepsilon \rightharpoonup \dot{F}\) in \(L^2(Q;\mathbb {R}^{d\times d})\) we obtain
With the coercive and quadratic structure of \({\widehat{\zeta }}\) assumed in (2.30e) we proceed as follows:
where \(C_\varepsilon =F_\varepsilon ^\top F_\varepsilon ^{}\). We see that the first term converges by (6.10), while the second term converges by the weak convergence \(V_\varepsilon \rightharpoonup V\) and the strong convergence \( {\mathbb {D}}(C_\varepsilon ,\theta _\varepsilon ) V \rightarrow {\mathbb {D}}(C,\theta ) V\) (as \({\mathbb {D}}\) is bounded and the arguments converge pointwise). Similarly, \(\delta (\varepsilon )\rightarrow 0\) by Lebesgue’s dominated convergence theorem, and thus we conclude the strong convergence \(\Vert V_\varepsilon {-}V\Vert _{L^2(Q;\mathbb {R}^{d\times d})} \rightarrow 0\).
Step 5: Limit passage in the heat equation. Testing the regularized heat equation (4.1b) with boundary conditions (4.2c) by a smooth function v with \( v(T,\cdot )\equiv 0\) we find
Here the first term passes to the limit by \(\nabla \theta _\varepsilon \rightharpoonup \nabla \theta \) and \({\mathcal {K}}(\nabla y_\varepsilon , \theta _\varepsilon ) \nabla v \rightarrow {\mathcal {K}}(\nabla y, \theta )\). In the second term we use
Because of Step 4, we know \(V_\varepsilon \rightarrow V\) strongly in \(L^2( Q; \mathbb {R}^{d\times d}_\mathrm {sym} )\). Hence, we have \(g_\varepsilon \rightarrow g:=K|V|^2\) in \(L^1(Q)\) and may assume, after extracting another subsequence, \( V_\varepsilon (t,x)\rightarrow V(t,x)\) almost everywhere in Q. By the uniform/pointwise convergence of \(C_\varepsilon \) and \(\theta _\varepsilon \) for any \(v\in C^0(\overline{Q})\) we obtain
As the majorants \(g_\varepsilon \Vert v\Vert _{L^\infty (Q)}\) converge to \(g\Vert v\Vert _{L^\infty (Q)}\) in \(L^1(Q)\) the generalized dominated convergence theorem implies convergence of the second term in (6.11).
In the third term we have weak convergence of \(\nabla \dot{y}_\varepsilon \) and strong convergence of \(v\partial _F \phi (\nabla y_\varepsilon , \theta _\varepsilon )\). Similarly, the remaining four terms converge to the desired limits. Thus, we have shown that \((y,\theta )\) satisfy (2.27b), which finishes the proof of Proposition 6.4. \(\quad \square \)
Remark 6.5
(Strong convergence of\(y_{\varepsilon \tau }\)and\(y_\varepsilon \)). Strengthening the monotonicity of \({\mathfrak {h}}_\mathrm {el}(\cdot )\), implied by the convexity assumed in (2.30d), to the strict monotonicity
we can use the argumentation after (5.11) to show \(\overline{y}_{\varepsilon \tau }(t) \rightarrow y_\varepsilon (t) \) strongly in \(W^{2,p}(\varOmega ;\mathbb {R}^d)\) for all \(t\in [0,T]\). Similarly, in Proposition 6.4 one can show \(y_{\varepsilon }(t) \rightarrow y(t) \) strongly in \(W^{2,p}(\varOmega ;\mathbb {R}^d)\). Together with the \(L^\infty \)-estimate (4.9a), we can also strengthen the weak* convergence (5.3a) in \(L^\infty (I;W^{2,p}(\varOmega ;\mathbb {R}^d))\) to a strong convergence in \(L^q(I;W^{2,p}(\varOmega ;\mathbb {R}^d))\) for all \(q\in {[1,\infty [}\). The same applies to (6.7a).
Remark 6.6
(Dynamical problems). Introducing the kinetic energy\(\frac{1}{2}\varrho |\dot{y}|^2\) with a mass density \(\varrho =\varrho (x)>0\) leads to an inertial force\(\varrho \ddot{y}\) in the momentum equation (2.13a), which would make the nonlinear problem hyperbolic. It is generally recognized as analytically very troublesome. Here, it would work for isothermal situations like in Corollary 2.3 if we were able to work with weak convergence, that is \({\mathscr {H}}\) needs to be quadratic (\(p=2\)). Staying with \({\mathcal {H}}\) depending on the second gradient \(\nabla ^2 y\) we would be forced to give up the determinant constraint \(\det \nabla y>0\), which is indeed possible if heat conduction is not considered. Alternatively, one may take \({\mathcal {H}}\) quadratic but coercive on the Hilbert space \(H^s(\varOmega )\) with \(s>1+d/2\), such that \(H^s(\varOmega )\) still embeds into \(C^{1,\alpha }\) for some \(\alpha >0\), cf. also [26, Sect. 9.3]. In the non-isothermal situation, it seems difficult to ensure that the acceleration \(\ddot{y}\in L^2(I;H^{1+\kappa }(\varOmega ;\mathbb {R}^{d\times d})\) stays in duality with the velocity \(\dot{y}\). Obtaining enough regularity is difficult and the higher-order viscosity is inevitably very nonlinear to comply with frame-indifference, while the corresponding generalization of Korn’s inequality does not seem to be available.
Remark 6.7
(Other transport processes: flow in porous media). Beside heat transport, one can also consider other transport processes in a similar way. The transport coefficients can be pulled back as in (2.24). For example, considering mass transport for a concentration c one has to make the free energy \(\psi \) also c-dependent and to augment it by a capillarity-like gradient term \(\frac{1}{2}\varkappa |\nabla c|^2\). The dissipation potential \({\mathcal {R}}\) will then be augmented by the nonlocal term \(\frac{1}{2} \Vert \mathcal {M} ( \nabla y,c)^{1/2}\nabla \Delta _{\mathcal {M}(\nabla y,c)}^{-1} \dot{c} \Vert ^2_{L^2(\varOmega )}\) with \(\Delta _{\mathcal {M}}^{-1}: f \mapsto \mu \) denoting the linear operator \(H^1(\varOmega )^*\rightarrow H^1(\varOmega )\) defined by the weak solution \(\mu \) to the equation \(\mathop {\hbox {div}}\nolimits (\mathcal {M}\nabla \mu )=f\). Considering the mobility tensor \({\mathbb {M}}={\mathbb {M}}(x,c)\), we can define the pulled-back tensor \({{\mathcal {M}}}(x,F,c):=({\mathrm {Cof}}\, F^\top ){\mathbb {M}}(x,c){\mathrm {Cof}}\, F/\det F\) and augment the system with a diffusion equation of Cahn–Hilliard type:
with \(\sigma _\mathrm {vi}\) as in (2.13a), \(c_\mathrm {v}(F,c,\theta )=-\theta \partial _{\theta \theta }^2\psi (F,c,\theta )\), and \(\xi \) from (2.10). In (6.12b), the variable \(\mu \) is called the chemical potential that is thermodynamically conjugate to c. One can also augment the model by some inelastic (plastic or creep-type) strain like in [45], where also the inertial forces are included, whereas viscosity is ignored and the restriction to small elastic strains is imposed.
References
Antman, S.S.: Physically unacceptable viscous stresses. Z. Angew. Math. Phys. 49, 980–988, 1998
Ball, J.M.: Constitutive inequalities and existence theorems in nonlinear elastostatics. Nonlinear Analysis and Mechanics: Heriot–Watt Symposium (Edinburgh, 1976), Vol. I, Pitman, London, 187–241. Res. Notes in Math., No. 17, 1977
Ball, J.M.: Some open problems in elasticity. Geometry, Mechanics, and Dynamics (Eds. P. Newton, P. Holmes, and A. Weinstein) Springer, New York, 3–59, 2002
Ball, J.M.: Progress and puzzles in nonlinear elasticity. Poly-, Quasi- and Rank-One Convexity in Applied Mechanics (Eds. J. Schröder and P. Neff), CISM Intl. Centre for Mech. Sci., vol. 516, Springer, Wien, 1–15, 2010
Barbu, V.: Nonlinear Differential Equations of Monotone Types in Banach Spaces. Springer, New York 2010
Batra, R.C.: Thermodynamics of non-simple elastic materials. J. Elasticity6, 451–456, 1976
Bonetti, E., Bonfanti, G.: Existence and uniqueness of the solution to a 3D thermoelastic system. Electron. J. Diff. Eqs. 50, 1–15, 2003
Ball, J.M., Crooks, E.C.M.: Local minimizers and planar interfaces in a phase-transition model with interfacial energy. Calc. Var. 40, 501–538, 2011
Boccardo, L., Dall’aglio, A., Gallouët, T., Orsina, L.: Nonlinear parabolic equations with measure data. J. Funct. Anal. 147, 237–258, 1997
Betounes, D.E.: Kinematics of submanifolds and the mean curvature normal. Arch. Rational Mech. Anal. 96, 1–27, 1986
Boccardo, L., Gallouët, T.: Non-linear elliptic and parabolic equations involving measure data. J. Funct. Anal. 87, 149–169, 1989
Blanchard, D., Guibé, O.: Existence of a solution for a nonlinear system in thermoviscoelasticity. Adv. Diff. Eq. 5, 1221–1252, 2000
Brézis, H.: Operateur maximaux monotones et semi-groupes de contractions dans les espaces de hilbert. North-Holland, Amsterdam 1973
Dafermos, C.M.: Global smooth solutions to the initial boundary value problem for the equations of one-dimensional thermoviscoelasticity. SIAM J. Math. Anal. 13, 397–408, 1982
Demoulini, S.: Weak solutions for a class of nonlinear systems of viscoelasticity. Arch. Ration. Mech. Anal. 155, 299–334, 2000
Dal Maso, G., Lazzaroni, G.: Quasistatic crack growth in finite elasticity with non-interpenetration. Ann. Inst. H. Poinc. Anal. Non Lin. 27(1), 257–290, 2010
Duda, F.P., Souza, A.C., Fried, E.: A theory for species migration in a finitely strained solid with application to polymer network swelling. J. Mech. Phys. Solids58, 515–529, 2010
Demoulini, S., Stuart, D., Tzavaras, A.: A variational approximation scheme for three dimensional elastodynamics with polyconvex energy. Arch. Rational Mech. Anal. 157, 325–344, 2001
Fried, E., Gurtin, M.E.: Tractions, balances, and boundary conditions for nonsimple materials with application to liquid flow at small-lenght scales. Arch. Ration. Mech. Anal. 182, 513–554, 2006
Friedrich, M., Kružík, M.: On the passage from nonlinear to linearized viscoelasticity. SIAM J. Math. Anal. 50, 4426–4456, 2018
Fonseca, I., Leoni, G.: Modern Methods in the Calculus of Variations: \(L^p\)Spaces. Springer, Berlin 2007
Feireisl, E., Málek, J.: On the Navier–Stokes equations with temperature-dependent transport coefficients. Diff. Equations Nonlin. Mech., 14pp (electronic), Art.ID 90616, 2006
Govindjee, S., Simo, J.C.: Coupled stress-diffusion: case II. J. Mech. Phys. Solids41, 863–887, 1993
Healey, T.J., Krömer, S.: Injective weak solutions in second-gradient nonlinear elasticity. ESAIM Control Optim. Cal. Var. 15, 863–871, 2009
Kružík, M., Pelech, P., Schlömerkemper, A.: Gradient polyconvexity in evolutionary models of shape-memory alloys. J. Optim. Theo. Appl. 184, 5–20, 2020
Kružík, M., Roubíček, T.: Mathematical Methods in Continuum Mechanics of Solids. Springer, Cham 2019
Lewicka, M., Mucha, P.B.: A local existence result for system of viscoelasticity with physical viscosity. Evol. Equ. Control Theory2, 337–353, 2013
Mindlin, R.D., Eshel, N.N.: On first strain-gradient theories in linear elasticity. Intl. J. Solid Struct. 4, 109–124, 1968
Mielke, A.: Formulation of thermoelastic dissipative material behavior using GENERIC. Contin. Mech. Thermodyn. 23, 233–256, 2011
Mielke, A.: Thermomechanical modeling of energy-reaction-diffusion systems, including bulk-interface interactions. Discr. Contin. Dyn. Syst. Ser. S6, 479–499, 2013
Mainik, A., Mielke, A.: Global existence for rate-independent gradient plasticity at finite strain. J. Nonlinear Sci. 19, 221–248, 2009
Mielke, A., Mittnenzweig, M.: Convergence to equilibrium in energy-reaction-diffusion systems using vector-valued functional inequalities. J. Nonlinear Sci. 28, 765–806, 2018
Mielke, A., Naumann, J.: On the Existence of Global-in-Time Weak Solutions and Scaling Laws for Kolmogorov’s Two-Equation Model of Turbulence, Preprints: WIAS, Berlin, 2545, 2018 (https://doi.org/10.20347/WIAS.PREPRINT.2545) and arXiv:1801.02039
Mielke, A., Ortner, C., Sengül, Y.: An approach to nonlinear viscoelasticity via metric gradient flows. SIAM J. Math. Anal. 46, 1317–1347, 2013
Mielke, A., Roubíček, T.: Rate-Independent Systems-Theory and Application. Springer, New York 2015
Mielke, A., Roubíček, T.: Rate-independent elastoplasticity at finite strains and its numerical approximation. Math. Models Methods Appl. Sci. 6, 2203–2236, 2016
Mielke, A., Rossi, R., Savaré, G.: Nonsmooth analysis of doubly nonlinear evolution equations. Calc. Var. PDE46, 253–310, 2013
Mielke, A., Rossi, R., Savaré, G.: Global existence results for viscoplasticity at finite strain. Arch. Ration. Mech. Anal. 227, 423–475, 2018
Neff, P.: On Korn’s first inequality with non-constant coefficients. Proc. R. Soc. Edinb. 132A, 221–243, 2002
Podio-Guidugli, P.: Contact interactions, stress, and material symmetry, for nonsimple elastic materials. Theor. Appl. Mech. 28–29, 261–276, 2002
Pompe, W.: Korn’s first Inequality with variable coefficients and its generalization. Comment. Math. Univ. Carolinae44, 57–70, 2003
Roubíček, T.: Models of microstructure evolution in shape memory alloys, Nonlinear Homogenization and Its Applications to Composites, Polycrystals and Smart Materials (Eds. P. Ponte Castaneda, J.J. Telega, and B. Gambin), Kluwer, Dordrecht, 269–304, 2004
Roubíček, T.: Thermo-visco-elasticity at small strains with \({L}^1\)-data. Q. Appl. Math. 67, 47–71, 2009
Roubíček, T.: Nonlinear Partial Differential Equations with Applications, 2nd edn. Birkhäuser, Basel 2013
Roubíček, T., Stefanelli, U.: Thermodynamics of elastoplastic porous rocks at large strains, earthquakes, and seismic waves. SIAM J. Appl. Math. 78, 2597–2625, 2018
Šilhavý, M.: Phase transitions in non-simple bodies. Arch. Ration. Mech. Anal. 88, 135–161, 1985
Stein, E., Sagar, G.: Theory and finite element computation of cyclic martensitic phase transformation with finite strain using umat. Int. J. Numer. Methods Eng. 74, 1–31, 2008
Steinmann, P.: Geometric Foundations of Continuum Mechanics. Springer, Heidelberg 2015
Stein, E., Zwickert, O.: Theory and finite element computations of a unified cyclic phase transformation model for monocrystalline materials at small strains. Comput. Mech. 40, 429–445, 2007
Triantafyllidis, N., Aifantis, E.C.: A gradient approach to localization of deformation. I. Hyperelastic materials. J. Elast. 16, 225–237, 1986
Toupin, R.A.: Elastic materials with couple stresses. Arch. Ration. Mech. Anal. 11, 385–414, 1962
Tvedt, B.: Quasilinear equations of viscoelasticity of strain-rate type. Arch. Ration. Mech. Anal. 189, 237–281, 2008
Visintin, A.: Models of Phase Transitions. Birkhäuser, Boston 1996
Acknowledgements
Open Access funding provided by Projekt DEAL. The authors are very thankful to two anonymous referees for a very thorough reading of the submitted version and for detecting many impurities. Alexander Mielke is grateful for the hospitality and support of Charles University and for partial support by Deutsche Forschungsgemeinschaft (DFG) via the SFB 1114 Scaling Cascades in Complex Systems (subproject B01 “Fault Networks and Scaling Properties of Deformation Accumulation”). Tomáš Roubíček is thankful for hospitality and support of the Weierstraß-Institut Berlin. Also the partial support of the Czech Science Foundation Projects 17-04301S (as for the focus to dissipative evolutionary systems), 18-03834S (as for the application in modeling of shape-memory alloys), and 19-29646L (as for the focus to large strains) also through the FWF Grant I 4052 N32 and from BMBWF through the OeAD-WTZ Project CZ04/2019, as well as through the institutional support RVO: 61388998 (ČR) is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by G. Dal Maso.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
In memory of Erwin Stein, who advocated the importance of large-strain elasticity in engineering practice.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mielke, A., Roubíček, T. Thermoviscoelasticity in Kelvin–Voigt Rheology at Large Strains. Arch Rational Mech Anal 238, 1–45 (2020). https://doi.org/10.1007/s00205-020-01537-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-020-01537-z