Abstract
Using six years of spectroscopic monitoring of the luminous quasar HE 0435-4312 (z = 1.2231) with the Southern African Large Telescope, in combination with photometric data (CATALINA, OGLE, SALTICAM, and BMT), we determined a rest-frame time delay of  days between the Mg ii broad-line emission and the ionizing continuum using seven different time-delay inference methods. Time-delay artifact peaks and aliases were mitigated using the bootstrap method and prior weighting probability function, as well as by analyzing unevenly sampled mock light curves. The Mg ii emission is considerably variable with a fractional variability of ∼5.4%, which is comparable to the continuum variability (∼4.8%). Because of its high luminosity (L3000 = 1046.4 erg s−1), the source is beneficial for a further reduction of the scatter along the Mg ii-based radius–luminosity relation and its extended versions, especially when the highly accreting subsample that has an rms scatter of ∼0.2 dex is considered. This opens up the possibility of using the high-accretor Mg ii-based radius–luminosity relation for constraining cosmological parameters. With the current sample of 27 reverberation-mapped sources, the best-fit cosmological parameters (Ωm, ΩΛ) = (0.19; 0.62) are consistent with the standard cosmological model within the 1σ confidence level.
days between the Mg ii broad-line emission and the ionizing continuum using seven different time-delay inference methods. Time-delay artifact peaks and aliases were mitigated using the bootstrap method and prior weighting probability function, as well as by analyzing unevenly sampled mock light curves. The Mg ii emission is considerably variable with a fractional variability of ∼5.4%, which is comparable to the continuum variability (∼4.8%). Because of its high luminosity (L3000 = 1046.4 erg s−1), the source is beneficial for a further reduction of the scatter along the Mg ii-based radius–luminosity relation and its extended versions, especially when the highly accreting subsample that has an rms scatter of ∼0.2 dex is considered. This opens up the possibility of using the high-accretor Mg ii-based radius–luminosity relation for constraining cosmological parameters. With the current sample of 27 reverberation-mapped sources, the best-fit cosmological parameters (Ωm, ΩΛ) = (0.19; 0.62) are consistent with the standard cosmological model within the 1σ confidence level.
Export citation and abstract BibTeX RIS
1. Introduction
Broad emission lines with line widths of several thousand km s−1 are one of the main characteristic features of the optical and UV spectra of active galactic nuclei (AGNs; Seyfert 1943; Woltjer 1959; Schmidt 1963), specifically of type I, where the broad-line region (BLR) is not obscured by the dusty molecular torus (Antonucci 1993; Urry & Padovani 1995). However, the scattered polarized light can reveal broad lines even for obscured type II AGNs (type II NGC 1068 was the first case, Antonucci & Miller 1985), which implies the universal presence of the BLR for accreting supermassive black holes (SMBHs). Low-luminosity systems, such as the Galactic Center (Genzel et al. 2010; Eckart et al. 2017; Zajaček et al. 2018) or M87 (Sabra et al. 2003), do not reveal the presence of broad lines. But broad lines can be present even for some sources with lower accretion rates (Bianchi et al. 2019), and the exact accretion limit for their appearance was analyzed to some extent by, e.g., Elitzur & Ho (2009), who estimated a bolometric luminosity limit of  , where M• is the black hole mass in units of 107 solar masses (M⊙). However, several crucial questions remain unanswered. Mainly the transition from geometrically thin disk accretion flows to geometrically thick advection-dominated accretion flows at lower accretion rates is still unclear and is likely related to the boundary conditions, the ability of the flow to cool, the feeding mechanism (warm stellar winds or an inflow of cold gas from larger scales), the associated initial angular momentum, and the resulting circularization radius. In addition, not only the formation of the BLR but also its properties seem to depend on the accretion rate, which motivates the study of more highly accreting sources (Du et al. 2015, 2018), such as HE 0413-4031 in particular (Zajaček et al. 2020).
, where M• is the black hole mass in units of 107 solar masses (M⊙). However, several crucial questions remain unanswered. Mainly the transition from geometrically thin disk accretion flows to geometrically thick advection-dominated accretion flows at lower accretion rates is still unclear and is likely related to the boundary conditions, the ability of the flow to cool, the feeding mechanism (warm stellar winds or an inflow of cold gas from larger scales), the associated initial angular momentum, and the resulting circularization radius. In addition, not only the formation of the BLR but also its properties seem to depend on the accretion rate, which motivates the study of more highly accreting sources (Du et al. 2015, 2018), such as HE 0413-4031 in particular (Zajaček et al. 2020).
The BLR has mostly been studied indirectly via reverberation mapping, i.e., by inferring the time delay between the ionizing UV continuum emission of an accretion disk and the broad-line emission (Blandford & McKee 1982; Peterson & Horne 2004; Gaskell 2009; Czerny 2019; Popović 2020) using typically the interpolated cross-correlation function (Peterson et al. 1998, 2004; Sun et al. 2018) or other methods (see, e.g., Zajaček et al. 2019, 2020, for an overview and an application of seven methods in total). The high correlation between the continuum and the line-emission fluxes implies that the line emission is mostly reprocessed thermal emission from an accretion disk. From the rest-frame time delay τBLR, it is straightforward to estimate the size of the BLR, RBLR = c τBLR, and in combination with the single-epoch line FWHM or the line dispersion σ, which serve as proxies for the BLR virial velocity, one can infer the central black hole mass, M• = fc τBLRFWHM2 G−1. The factor f is known as the virial factor and takes into account the geometrical and kinematic characteristics of the BLR. Although f is typically of the order of unity, it introduces a factor of ∼2–3 uncertainty in the black hole mass. By comparing the black hole masses inferred from accretion-disk spectra with the masses from single-epoch spectroscopy, Mejía-Restrepo et al. (2018) found that the value of f is approximately inversely proportional to the broad-line FWHM, 9 which provides a way to better estimate f for individual sources.
Optical reverberation mapping studies using the Hβ line showed that there is a simple power-law relation between the size of the BLR and the monochromatic luminosity of AGNs at 5100 Å (Kaspi et al. 2000; Peterson et al. 2004), the so-called radius–luminosity (RL) relation. After a proper removal of the host galaxy starlight (Bentz et al. 2013), the slope of the power law is close to 0.5, which is expected from simple photoionization arguments. The importance of the radius–luminosity relation lies in its application to infer black hole masses from single-epoch spectroscopy, where FWHM or the line dispersion σ serves as a proxy for the velocity of virialized BLR clouds, and the monochromatic luminosity of the source serves as a proxy for the rest-frame time delay, and hence the BLR radius, via the RL relation.
Another, more recent application of the RL relation is the possibility to utilize it for obtaining absolute monochromatic luminosities. From the measured flux densities, one can calculate luminosity distances and use them for constraining cosmological parameters (Haas et al. 2011; Watson et al. 2011; Czerny et al. 2013, 2020; Martínez-Aldama et al. 2019; Panda et al. 2019). The problem for cosmological applications is that the RL relation exhibits a scatter, which has increased with the accumulation of more sources, especially those with higher accretion rates (super-Eddington accreting massive black holes—SEAMBHs; Du et al. 2015, 2018).
The scatter is present both for lower-redshift Hβ sources (Grier et al. 2017) and for higher-redshift Mg ii sources, which follow an analogous RL relation (Czerny et al. 2019; Homayouni et al. 2020; Zajaček et al. 2020). The scatter was attributed to the accretion-rate intensity, with the basic trend that the largest departure from the nominal RL relation is exhibited by the highly accreting sources (Du et al. 2018). The correction to the time delay was proposed based on the Eddington ratio and the dimensionless accretion rate (Martínez-Aldama et al. 2019); however, these two quantities depend on the time delay via the black hole mass. To break down the interdependence, Fonseca Alvarez et al. (2020) proposed to make use of independent, observationally inferred quantities related to the optical/UV spectral energy distribution (SED). The relative Fe II strength correlated with the accretion-rate intensity is especially efficient in reducing the scatter for Hβ sources to only 0.19 dex (Du & Wang 2019; Yu et al. 2020a). The same effect is observed for the extended radius–luminosity relations for Mg ii reverberation-mapped sources (68 sources; Martínez-Aldama et al. 2020). Martínez-Aldama et al. (2020) divide the sources into low and high accretors, where the high accretors show a much smaller scatter of only ∼0.2 dex. The extended RL relation including the relative Fe II strength further reduces the scatter down to 0.17 dex for the highly accreting subsample.
Large reverberation monitoring campaigns are currently performed by several groups, for instance the Australian Dark Energy Survey (OzDES, Hoormann et al. 2019), the Sloan Digital Sky Survey Reverberation Mapping project (SDSS-RM, Shen et al. 2015, 2019), the Dark Energy Survey (DES, Abbott et al. 2018; Diehl et al. 2018; Yang et al. 2020), the SEAMBHs (Du et al. 2015, 2018), but monitoring of an individual source can also contribute significantly, especially if its luminosity is an extreme value in the radius–luminosity relation. This is because the most luminous quasars have very low sky densities, so they are not suitable for reverberation mapping multi-object spectroscopy (MOS-RM) programs, and instead require monitoring of individual objects. This is why programs such as the one presented here are necessary. Luminous sources are expected to be beneficial in terms of increasing the RL correlation coefficient, and this can also lead to a reduction in the scatter. In the current paper, we present results of the time delay of the Mg ii line for the last of three very luminous quasars at intermediate redshift monitored for several years with the Southern African Large Telescope (SALT). The source HE 0435-4312 (z = 1.2231) hosts a supermassive black hole of 2.2 × 109 M⊙ that is highly accreting with an Eddington ratio of 0.58 according to the SED best-fit of Sredzińska et al. (2017). The peculiarity of the source is a smooth shift of the peak of the Mg ii line first toward longer wavelengths, while currently the shift proceeds toward shorter wavelengths. This line shift could hint at the presence of a supermassive black hole binary (Sredzińska et al. 2017).
In this paper, we measure the time delay of HE 0435-4312 using seven methods. Subsequently, we study the position of the source in the RL relation, including its extended versions, and how the source affects the correlation coefficient as well as the scatter. Finally, we look at the potential applicability of the Mg ii highly accreting subsample for cosmological studies.
The paper is structured as follows. In Section 2, we describe observations including both spectroscopy and photometry. In Section 3, we analyze the mean and the rms spectra, spectral fits of individual observations, and the variability of the continuum and the line-emission light curves. The core of the paper is Section 4, where we summarize the mean rest-frame time delay between the Mg ii emission and the continuum as inferred from seven different methods. The position of the source in the RL relation and its extended versions is also analyzed in this section. Subsequently, in Section 5, we discuss the aspect of variability of the Mg ii emission as well as the application of the highly accreting Mg ii subsample in cosmology. Finally, we present our conclusions in Section 6.
2. Observations
Here we present the optical photometric and spectroscopic observations of the quasar HE 0435-4312 (z = 1.232, V = 17.1 mag) with J2000 coordinates R.A. = 04h37m11 8, decl. = −43°06'04ʺ according to the NED database.
10
Due to its large optical flux density, it was found during the Hamburg ESO quasar survey (Wisotzki et al. 2000). Previously, Sredzińska et al. (2017) reported ten spectroscopic observations performed by SALT Robert Stobie Spectrograph (RSS) over the course of three years (from 2012 December 23/24 to 2015 December 7/8). The main result of their analysis was the detection of the fast displacement of the Mg ii line with respect to the quasar rest frame by 104 ± 14 km s−1 yr−1. In this paper the number of spectroscopic observations increased to 25, which together with 81 photometric measurements allows for the analysis of the time-delay response of the Mg ii line with respect to the variable continuum. Previously we detected a time delay for two other luminous quasars:
8, decl. = −43°06'04ʺ according to the NED database.
10
Due to its large optical flux density, it was found during the Hamburg ESO quasar survey (Wisotzki et al. 2000). Previously, Sredzińska et al. (2017) reported ten spectroscopic observations performed by SALT Robert Stobie Spectrograph (RSS) over the course of three years (from 2012 December 23/24 to 2015 December 7/8). The main result of their analysis was the detection of the fast displacement of the Mg ii line with respect to the quasar rest frame by 104 ± 14 km s−1 yr−1. In this paper the number of spectroscopic observations increased to 25, which together with 81 photometric measurements allows for the analysis of the time-delay response of the Mg ii line with respect to the variable continuum. Previously we detected a time delay for two other luminous quasars:  days for CTS C30.10 (Czerny et al. 2019) and
days for CTS C30.10 (Czerny et al. 2019) and  days for HE 0413-4031 (Zajaček et al. 2020), both in the rest frames of the corresponding source. These intermediate-redshift sources are very important for constraining the Mg ii-based radius–luminosity relation. Especially sources with either low or high luminosities are needed to constrain the slope of the RL relation and evaluate the scatter along it (Martínez-Aldama et al. 2020).
days for HE 0413-4031 (Zajaček et al. 2020), both in the rest frames of the corresponding source. These intermediate-redshift sources are very important for constraining the Mg ii-based radius–luminosity relation. Especially sources with either low or high luminosities are needed to constrain the slope of the RL relation and evaluate the scatter along it (Martínez-Aldama et al. 2020).
2.1. Photometry
The photometric data were combined from a few dedicated monitoring projects, described in more detail in Zajaček et al. (2020). The source has been monitored in the V band as part of the OGLE-IV survey (Udalski et al. 2015) done with the 1.3 m Warsaw telescope at the Las Campanas Observatory, Chile. The exposure times were typically around 240 s, and the photometric errors were small, of the order of 0.005 magnitude (see Table 3). In the later epochs the quasar was observed, again in the V band, with the 40 cm Bochum Monitoring Telescope (BMT).
11
These data showed a systematic offset of 0.2 magnitudes toward larger magnitudes with respect to the overlapping OGLE data, which we corrected for by the shift of all of the BMT points. SALT spectroscopic observations were also supplemented, whenever possible with SALTICAM imaging in the g band. We have analyzed all of these data; however, two data sets (2013 August 20 and 2019 January 27) showed a significant discrepancy with the other measurements. The first of the two sets of observations was done during full moon, and with the moon–target separation relatively large; spectroscopic observations were not affected, but the photometric observations were. During the second set of observations the night was dark but seeing was about 2 5 during the photometry, dropping down to 2'' during the spectroscopic exposures. We were unable to correct the data for these effects, and we did not include these data points in further considerations. Because of the collection of the data in the g band, we allowed for the grayshift of all the SALTICAM data, and the shift was determined using epochs when they coincided with the more precise OGLE set collected in the V band. Finally, we supplemented our photometry with the light curve from the Catalina Sky Survey,
12
which is not of a very high quality (with uncertainties of 0.02–0.03 mag) but nicely covers the early period from 2005 until 2013. We have binned these data to reduce the scatter. Table 3 contains only the data points that were used in time-delay measurements. All the data points are presented in the upper panel of Figure 1.
5 during the photometry, dropping down to 2'' during the spectroscopic exposures. We were unable to correct the data for these effects, and we did not include these data points in further considerations. Because of the collection of the data in the g band, we allowed for the grayshift of all the SALTICAM data, and the shift was determined using epochs when they coincided with the more precise OGLE set collected in the V band. Finally, we supplemented our photometry with the light curve from the Catalina Sky Survey,
12
which is not of a very high quality (with uncertainties of 0.02–0.03 mag) but nicely covers the early period from 2005 until 2013. We have binned these data to reduce the scatter. Table 3 contains only the data points that were used in time-delay measurements. All the data points are presented in the upper panel of Figure 1.
Figure 1. Light curves and the time evolution of emission line properties measured in the rest frame. Points marked with a black circle (obs. 19) were removed from the analysis.
Download figure:
Standard image High-resolution imageRecently, the quasar was monitored in the V band with a median sampling of 14 days using Lesedi, a 1 m telescope at the South African Astronomical Observatory (SAAO), with the Sutherland High Speed Optical Camera (SHOC). SHOC has a 5.7 × 5.7 arcmin2 field of view (FoV). Each observation consists of nine dithered 60 s exposures. They are corrected for bias and flatfields (using dusk or dawn sky flats). Astrometry is obtained using the SCAMP tool. 13 The resulting median-combined image has a 7.5 × 7.5 arcmin2 FoV centered on the quasar. The light curves were created using five calibration stars located on the same image as the quasar. The preliminary results are consistent with the last photometric point from SALT/SALTICAM.
2.2. Spectroscopy
Spectroscopic observations of HE 0435-4312 were performed with the 11 m telescope SALT, with the RSS (Burgh et al. 2003; Kobulnicky et al. 2003; Smith et al. 2006) in a long-slit mode and a slit width of 2''. We used the RSS PG1300 grating with a grating tilt angle of 26 75. Order blocking was done with the blue PC04600 filter. Two exposures were always made, each of about 820 s. The same setup has been used throughout the whole monitoring period, from 2012 December 23 until 2020 August 20. Observations were always performed in the service mode.
75. Order blocking was done with the blue PC04600 filter. Two exposures were always made, each of about 820 s. The same setup has been used throughout the whole monitoring period, from 2012 December 23 until 2020 August 20. Observations were always performed in the service mode.
The raw data reduction was performed by the SALT observatory staff, and the final reduction was performed by us with the use of the IRAF package. All the details were given in Sredzińska et al. (2017), where the results from the first three years of this campaign were presented. We followed exactly the same procedure for all 25 observations to minimize the possibility of unwanted systematic differences.
In order to get the flux calibration, we performed a weighted spline interpolation of the first order (with inverse measurement errors as weights) between the epochs of photometric and spectroscopic observations, thus an apparent V magnitude was assigned to each spectrum. Taking as a reference the composite spectrum and the continuum with a slope of αλ = −1.56 from Vanden Berk et al. (2001), we just normalized each spectrum to the V magnitudes (5500 Å).
2.3. Spectroscopic Data Fitting
The reduced and calibrated spectra were fitted in the 2700–2900 Å range in the rest frame. The basic model components were as in Sredzińska et al. (2017). The data were represented by (i) continuum in the form of a power law with arbitrary slope and normalization, (ii) the Fe II pseudocontinuum, and (iii) two kinematic components representing the Mg ii line; each of the kinematic components was represented by two doublet components. The line is unresolved, and the doublet ratio could not be well constrained, so it was fixed at 1:1 (see Sredzińska et al. 2017 for the discussion). For the kinetic shapes we used Lorentzian profiles since they provided somewhat better representation of the data in χ2 terms than Gaussian ones. All the parameters were fitted simultaneously. In order to determine the redshift and the most appropriate Fe II template, we studied in detail observation 23, which also covered the region around 3000 Å in the rest frame (see Appendix B). Thus for the adopted redshift z = 1.2231, the Fe II template was very slightly modified in comparison with Sredzińska et al. (2017), and the pseudocontinuum was kept at FWHM of 3100 km s−1. Thus there were eight free parameters in the model: power-law normalization and slope, normalization of the Fe II pseudocontinuum, the width and normalizations of the two kinematic components of Mg ii, and the position of the second component, with the other one set at the quasar rest frame, together with Fe II.
3. Results: Spectroscopy
3.1. Determination of the Mean and the rms Spectra
We determined the mean and the rms spectra for HE 0435-4312 as we did previously for quasar HE 0413-4031 (Zajaček et al. 2020). Due to the particularly low signal-to-noise ratio (∼7.5) shown by spectrum no. 19, which is clearly an outlier in the light curve (Figure 1), we do not consider it for the estimation of the mean and rms spectra. We followed the methodology for constructing the mean and the rms spectra as outlined in Peterson et al. (2004). In particular, we formed the mean spectrum (without spectrum no. 19) using
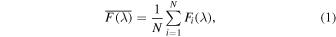
where Fi (λ) is the ith spectrum out of a total of N spectra in the measured database. Subsequently, the rms spectrum, initially taking into account all spectral components (Mg ii line + continuum + Fe II pseudocontinuum), was constructed using
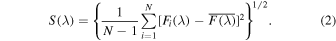
The constructed mean and rms spectra are shown in Figure 2 (black solid lines) in the upper and upper middle panels, respectively. The quasar is not strongly variable, so the normalization of the rms is very low, and the spectrum is noisy, with visible effects of occasional imperfect sky subtraction. However, the overall quality of the rms spectrum is still suitable for the analysis. In both the mean and the rms spectra, the Mg ii line modeling required two kinematic components, since line asymmetry is clearly visible. The result is shown in Figure 2 with spectral components depicted with different colored lines described in the figure caption. For the fitting, we finally used the redshift as determined by Sredzińska et al. (2017), but with a slightly modified Fe II template based on the d11 template of Bruhweiler & Verner (2008). We also compared and analyzed other Fe II templates based on the updated CLOUDY model (Ferland et al. 2017) as well as the six-transition model by Kovačević-Dojčinović & Popović (2015) and Popović et al. (2019). For a detailed discussion of different Fe II templates—a total of eight setups with different redshifts as well as Lorentzian or Gaussian line component profiles—see Appendix B.
Figure 2. Upper panel: mean spectrum (red curve) obtained without observation 19. We also show its decomposition into two Lorentzian components of the Mg ii line (dotted magenta), Fe II pseudocontinuum (dotted blue line), and a power law (green dashed line). Upper middle panel: rms spectrum and its decomposition. The notation of spectral components is the same as for the mean spectrum in the upper panel. Lower middle panel: the mean spectrum in absolute calibration. The solid black line denotes the mean spectrum including all the components (line, continuum, and Fe II pseudocontinuum). The red solid line indicates the mean spectrum constructed after removal of the continuum contribution from each spectrum. The blue solid line indicates the line-only mean spectrum after the additional removal of Fe II pseudocontinuum. Lower panel: a properly calibrated rms spectrum, with the black line denoting the total rms (line + continuum + Fe II pseudocontinuum). The rms spectrum after the subtraction of the continuum is shown by the red line, while the line-only rms is depicted by the blue line.
Download figure:
Standard image High-resolution imageThe overall shapes of the mean and the rms spectra are similar (see Figure 2). The FWHM of the Mg ii line in the mean spectrum is  ; the line in the rms spectrum might be slightly broader,
; the line in the rms spectrum might be slightly broader,  , but is consistent within the error margins. A much larger difference is seen in the line dispersion, which is much smaller in the mean spectrum than in the rms spectrum (
, but is consistent within the error margins. A much larger difference is seen in the line dispersion, which is much smaller in the mean spectrum than in the rms spectrum ( km s−1 versus
km s−1 versus  km s−1). The FWHM and σ are larger in the rms spectrum, most likely due to its noisy nature, although there is an indication of a trend of both Mg ii FWHM and σ being larger in the rms spectrum than in the mean spectrum based on the analysis of the SDSS-RM sample (Wang et al. 2019). However, the ratio of FWHM to σ for both the mean and the rms spectra is far from the value 2.35 expected for a Gaussian shape. The source can be classified as A-type according to the classification of Sulentic et al. (2000). This is consistent with the Eddington ratio 0.58 determined by Sredzińska et al. (2017) for this object. There is also an interesting change in the line position between the mean and the rms spectra, as determined from the first moment of the distribution: 2805 Å versus 2792 Å.
km s−1). The FWHM and σ are larger in the rms spectrum, most likely due to its noisy nature, although there is an indication of a trend of both Mg ii FWHM and σ being larger in the rms spectrum than in the mean spectrum based on the analysis of the SDSS-RM sample (Wang et al. 2019). However, the ratio of FWHM to σ for both the mean and the rms spectra is far from the value 2.35 expected for a Gaussian shape. The source can be classified as A-type according to the classification of Sulentic et al. (2000). This is consistent with the Eddington ratio 0.58 determined by Sredzińska et al. (2017) for this object. There is also an interesting change in the line position between the mean and the rms spectra, as determined from the first moment of the distribution: 2805 Å versus 2792 Å.
Following the spectral studies by Barth et al. (2015) and Wang et al. (2019), we show in Figure 2 (lower middle and lower panels) the mean and the rms spectra constructed taking into account all the spectral components (black lines; Mg ii line + continuum + Fe II pseudocontinuum), the mean and the rms spectra that have the continuum power law subtracted from each spectrum (red lines), and finally the spectra with Fe II pseudocontinuum subtracted from individual spectra, which represents the true, line-only mean and the rms spectrum (blue lines). For the rms spectra, we do not detect any significant difference in the line width, which is expected to be smaller for the total-flux rms than for the line-only rms spectrum (Barth et al. 2015; Wang et al. 2019). This can be attributed to the overall noisy nature of our rms spectra, which are constructed from only 24 individual spectra. According to Barth et al. (2015) and Wang et al. (2019), the difference in the line width becomes smaller for a sufficiently long duration of the campaign. However, in our case, the spectroscopic monitoring was only ∼4.25 times longer than the emission-line time lag in the observer's frame (see Section 4). For such a short duration, the distribution of the ratios of line width between the total-flux and the line-only rms spectra is broad—between 0.5 and 1.0, with the peak close to 1.0; see Appendix C in Barth et al. (2015).
3.2. Spectral Fits of Individual Observations
The fits to individual spectroscopic data sets were done in the same way as for the mean spectrum. In all 25 data sets, two kinematic components of the Mg ii line were needed to represent the line shape well. The normalization of Fe II pseudocontinuum was allowed to vary for each individual spectrum, while the Fe II width was fixed to FWHM = 3100 km s−1. The Mg ii component kinematically related to the Fe II is slightly narrower, having an average FWHM of 2128 ± 28 km s−1, while the second shifted component is somewhat broader, with FWHM of 2262 ± 90 km s−1. However, we stress here that the broadband modeling by Sredzińska et al. (2017) did not support any identification of these components with separate regions, so the two components are just a mathematical representation of the slightly asymmetric line shape.
The parameters for observation 19 were considerably different, but as we already mentioned in Section 3.1, this observation was of a particularly low quality despite the fact that actually three exposures were made this time. Cirrus clouds were present during the whole night, and even more clouds started arriving during the second exposure of the quasar, so the third exposure was done. Nevertheless, all the parameters were determined with errors a few times larger than for the remaining observations.
The average value of the equivalent width of the Mg ii line is 23.6 ± 0.5 Å if observation 19 is included. If observation 19 is not taken into account, the mean value increases to 24.1 ± 0.6 Å, and this is similar to the value determined from the mean spectrum: 23.9 Å. Such values are perfectly in agreement with the properties of the bright quasar sample studied by Forster et al. (2001), where the mean EW of the Mg ii broad component was found to be  Å. We do not see any traces of the narrow component in either the mean spectrum or the individual data sets.
Å. We do not see any traces of the narrow component in either the mean spectrum or the individual data sets.
The average value of the EW of Fe II, 18.2 ± 0.7 Å, is also similar to the value in the mean spectrum, 18.9 Å. The relative error is larger than for the Mg ii line since Fe II pseudocontinuum is more strongly coupled to the power-law continuum during the fitting procedure.
The dispersion in the measurements between observations partially represents the statistical errors, but partially reflect the intrinsic evolution of the source in time. This evolution is studied in the next section.
3.3. Light Curves: Variability and Trends
The quasar HE 0435-4312 is not strongly variable in terms of the continuum emission. The whole photometric light curve, including the CATALINA data, covers 14 yr, and the fractional variability amplitude for the continuum is 8.9% in flux. During the period covered by SALT data (7 yr) it is ∼4.9%. Fortunately, the Mg ii line flux shows significant variability, comparable to the continuum, at the level of 5.4% during this period. We do not observe a suppressed Mg ii variability in this source, unlike that seen in much larger samples (Goad et al. 1999; Woo 2008; Zhu et al. 2017). Yang et al. (2020) also detect the response of Mg ii emission to the continuum for 16 extreme-variability quasars, but with a smaller variability amplitude,  . A low Mg ii variability was modeled to be the result of a relatively large Eddington ratio (Guo et al. 2020) but HE 0435-4312 is also a source with a rather large Eddington ratio of 0.58 (Sredzińska et al. 2017). Overall, the fractional variability of the Mg ii line for our source is comparable to a variability of ∼10% on 100 day timescales as inferred for the SDSS-RM ensemble study (Sun et al. 2015).
. A low Mg ii variability was modeled to be the result of a relatively large Eddington ratio (Guo et al. 2020) but HE 0435-4312 is also a source with a rather large Eddington ratio of 0.58 (Sredzińska et al. 2017). Overall, the fractional variability of the Mg ii line for our source is comparable to a variability of ∼10% on 100 day timescales as inferred for the SDSS-RM ensemble study (Sun et al. 2015).
The variations in quasar parameters are smooth overall. The quality of observation 6 was not very high, as discussed in Sredzińska et al. (2017), but it still allowed the Mg ii line parameters to be obtained properly. However, observation 19 created considerable problems. The registered number of photons was much lower (by a factor of a few) than in typical observations, even the background was rather low, and clouds were apparently present in the sky. We did the data fitting, and the derived values of the model parameters form clear outliers when compared with the trends (see Figure 1). Therefore, we did not use this observation in the remaining analysis and the determination of the time delay.
In Sredzińska et al. (2017) the change of the line position was discussed in much detail, since during the first three years the Mg ii line seems to move systematically toward longer wavelength with a surprising speed of 104 ± 14 km s−1 yr−1 with respect to the quasar rest frame. However, now this trend has seemingly stopped, and in recent observations it seems to have reversed. Such emission line behavior is frequently considered as a signature of a binary black hole (e.g., Popović 2012 for a review). However, to claim such a phenomenon would require extensive tests that are beyond the current paper, which is aimed at measurement of the time delay of the Mg ii line.
4. Results: Time-delay determination
To determine the most probable time delay between the continuum and Mg ii line emission, we applied several methods as previously in Czerny et al. (2019) and Zajaček et al. (2020), namely:
- 1.interpolated cross-correlation function (ICCF),
- 2.discrete correlation function (DCF),
- 3.z-transformed discrete correlation function (zDCF),
- 4.the JAVELIN package,
- 5.measures of data regularity/randomness—von Neumann and Bartels estimators,
- 6.χ2 method.
These seven methods are described in detail in Appendix C, including their strengths over other methods. It is beneficial to compare more methods since our light curves are irregularly sampled and the continuum light curve is heterogeneous, i.e., coming from four different instruments (CATALINA, OGLE, SALTICAM, and BMT). After the exclusion of low-quality data points and outliers, we finally obtained 79 continuum measurements with a mean cadence of 69.0 days (maximum 597.6 days, minimum 0.75 days) and 24 Mg ii light-curve data points with a mean cadence of 121.6 days (maximum 398.9 days, minimum 25.9 days).
For our set of light curves, there were several candidate time delays present for different methods. A significant time delay between 600 and 700 days in the observer's frame was present for all the methods and we summarize the obtained values for this peak in Table 1 for the d11 Fe II template and the redshift of z = 1.2231. The time delay is not affected significantly by a different Fe II template, in particular the template of Kovačević-Dojčinović & Popović (2015) and Popović et al. (2019) (hereafter denoted as KDP15) with a slightly different best-fit redshift of z = 1.2330. The ICCF peak for KDP15 is at 692 days for the observer's frame; see Figure 13 in Appendix C.
Fe II template and the redshift of z = 1.2231. The time delay is not affected significantly by a different Fe II template, in particular the template of Kovačević-Dojčinović & Popović (2015) and Popović et al. (2019) (hereafter denoted as KDP15) with a slightly different best-fit redshift of z = 1.2330. The ICCF peak for KDP15 is at 692 days for the observer's frame; see Figure 13 in Appendix C.
Table 1. Overview of the Best Time Delays for Different Methods
| Method | Time Delay in the Observer's Frame (days) |
|---|---|
| ICCF |

|
| DCF |

|
| zDCF |

|
| JAVELIN |

|
| von Neumann estimator |

|
| Bartels estimator |

|
| χ2 method |

|
| Observer's frame mean |

|
| Rest-frame mean (z = 1.2231) |

|
Note. The time delay is expressed in light-days in the observer's frame. The last two rows contain the mean time delays in the observer's frame and in the rest frame for a redshift of z = 1.2231.
Download table as: ASCIITypeset image
The significance of the peak between 600 and 700 days was evaluated using the bootstrap method for several time-delay techniques, i.e., by randomly selected light-curve subsets. In addition, for the JAVELIN method, we applied alias mitigation using downweighting by the number of overlapping data points; see Appendix C.4. With this technique (see also Grier et al. 2017), secondary peaks for a time delay longer than 700 days could effectively be suppressed. For the assessment of other time-delay artifact peaks, we generated mock light curves using the Timmer–Koenig algorithm (Timmer & Koenig 1995) with the same light-curve cadence as the observed one; see Appendix D for a detailed discussion. From the constructed time-delay probability distributions for all the seven methods, we could identify clear artifacts due to the sampling for time delays ≲200 days as well as for ≳800 days in the observer's frame. The recovery of the true time delay appears to be challenging for the given cadence and the duration of the observations, but the combination of more methods is beneficial in identifying the best candidate for the true time delay.
4.1. Final Time Delay for the Mg ii Line
Combining all the seven methods listed in Table 1, the mean value in the observer's frame is  days. We visually compare the continuum light curve and the original as well as the time-shifted light curve of the Mg ii line in Figure 3. For an easier comparison, the Mg ii line is shifted toward larger magnitudes by the difference in the mean values of the two light curves (1.74 mag). The correlation between the continuum and the shifted Mg ii light curve, although present, is not visually improved with respect to the zero time lag. This is not unexpected since our source does not exhibit such a large variability amplitude as sources with a low Eddington ratio. In addition, even when the line-emission light curve is shifted by the fiducial time delay, it can intrinsically exhibit periods when the line emission is decorrelated with respect to the continuum emission, which is referred to as the emission-line or the BLR holiday (studied in more detail for NGC 5548, Dehghanian et al. 2019). This justifies the need to use several robust statistical methods to assess the best time delay. We also tried to subtract a linear trend from both light curves, but since for both of them the slope is consistent with zero within fitting uncertainties, it did not yield an improvement. Even for a noticeable linear trend, as for instance for HE 0413-4031 (Zajaček et al. 2020), detrending actually led to a decrease in the correlation coefficient at the fiducial time delay. Hence, the subtraction of a linear trend should be tested on a larger set of sources to assess statistical relevance in terms of time-delay determination.
days. We visually compare the continuum light curve and the original as well as the time-shifted light curve of the Mg ii line in Figure 3. For an easier comparison, the Mg ii line is shifted toward larger magnitudes by the difference in the mean values of the two light curves (1.74 mag). The correlation between the continuum and the shifted Mg ii light curve, although present, is not visually improved with respect to the zero time lag. This is not unexpected since our source does not exhibit such a large variability amplitude as sources with a low Eddington ratio. In addition, even when the line-emission light curve is shifted by the fiducial time delay, it can intrinsically exhibit periods when the line emission is decorrelated with respect to the continuum emission, which is referred to as the emission-line or the BLR holiday (studied in more detail for NGC 5548, Dehghanian et al. 2019). This justifies the need to use several robust statistical methods to assess the best time delay. We also tried to subtract a linear trend from both light curves, but since for both of them the slope is consistent with zero within fitting uncertainties, it did not yield an improvement. Even for a noticeable linear trend, as for instance for HE 0413-4031 (Zajaček et al. 2020), detrending actually led to a decrease in the correlation coefficient at the fiducial time delay. Hence, the subtraction of a linear trend should be tested on a larger set of sources to assess statistical relevance in terms of time-delay determination.
Figure 3. Comparison of the continuum and the shifted Mg ii light curves. Top: the continuum and the original Mg ii light curve. Bottom: the continuum and the Mg ii light curve shifted by the mean time delay of 658 days in the observer's frame.
Download figure:
Standard image High-resolution imageSubsequently, we obtain the mean rest-frame value of  days for the redshift of z = 1.2231. The light-travel distance of the Mg ii emission zone can then be estimated as
days for the redshift of z = 1.2231. The light-travel distance of the Mg ii emission zone can then be estimated as  . The rest-frame time delay is comparable within uncertainties to the time delay of the previously analyzed highly accreting quasar HE 0413-4031 (z = 1.38, Zajaček et al. 2020).
. The rest-frame time delay is comparable within uncertainties to the time delay of the previously analyzed highly accreting quasar HE 0413-4031 (z = 1.38, Zajaček et al. 2020).
4.2. Estimate of Black Hole Mass
Taking into account the rest-frame time delay of  days and the Mg ii FWHM in the mean spectrum of
days and the Mg ii FWHM in the mean spectrum of  , we can estimate the central black hole mass under the assumption that Mg ii emission clouds are virialized. Using the anticorrelation between the virial factor and the line FWHM according to Mejía-Restrepo et al. (2018),
, we can estimate the central black hole mass under the assumption that Mg ii emission clouds are virialized. Using the anticorrelation between the virial factor and the line FWHM according to Mejía-Restrepo et al. (2018),
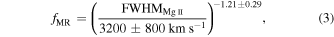
we obtain fMR ∼ 0.84. The virial black hole mass can then be calculated using the Mg ii FWHM in the mean spectrum and the measured time delay as  . Adopting the virial factor according to Woo et al. (2015), fWoo = 1.12 (based on FWHM of the Hβ line), we obtain the virial black hole mass
. Adopting the virial factor according to Woo et al. (2015), fWoo = 1.12 (based on FWHM of the Hβ line), we obtain the virial black hole mass  . Here we adopted the FWHM from the mean spectrum since it is better constrained than the rms FWHM. The mean values, however, are consistent within uncertainties, which is in agreement with the general correlation of Mg ii line widths measured in the mean and the rms spectra using the SDSS-RM sample (Wang et al. 2019).
. Here we adopted the FWHM from the mean spectrum since it is better constrained than the rms FWHM. The mean values, however, are consistent within uncertainties, which is in agreement with the general correlation of Mg ii line widths measured in the mean and the rms spectra using the SDSS-RM sample (Wang et al. 2019).
Using instead the Mg ii line dispersion in the mean spectrum,  , and the associated virial factor fσ
= 4.47 (based on the Hβ line dispersion) according to Woo et al. (2015), the black hole mass is estimated as
, and the associated virial factor fσ
= 4.47 (based on the Hβ line dispersion) according to Woo et al. (2015), the black hole mass is estimated as  . This value is consistent with the value inferred from the broadband SED fitting using the model of a thin accretion disk according to Sredzińska et al. (2017), where they obtained MSED = 2.2 × 109
M⊙. Hence for our source, using the line dispersion inferred from the mean spectrum (the rms spectrum is too noisy to reliably measure σ) appears to be beneficial for constraining the virial SMBH mass. Using the FWHM yields a virial mass below that inferred from broadband fitting.
. This value is consistent with the value inferred from the broadband SED fitting using the model of a thin accretion disk according to Sredzińska et al. (2017), where they obtained MSED = 2.2 × 109
M⊙. Hence for our source, using the line dispersion inferred from the mean spectrum (the rms spectrum is too noisy to reliably measure σ) appears to be beneficial for constraining the virial SMBH mass. Using the FWHM yields a virial mass below that inferred from broadband fitting.
Next, we estimate the Eddington ratio. Using our continuum light curve, the mean V-band magnitude is 17.15 ± 0.09 mag. With the redshift of z = 1.2231 and the mean Galactic foreground extinction in the V band of 0.045 mag according to NED,
14
we determine the luminosity at 3000 Å, ![$\mathrm{log}({L}_{3000}[\mathrm{erg}\,{{\rm{s}}}^{-1}])={46.359}_{-0.034}^{+0.038}$](https://content.cld.iop.org/journals/0004-637X/912/1/10/revision2/apjabe9b2ieqn34.gif) , for which we apply the conversions of Kozłowski (2015). To estimate the bolometric luminosity, the corresponding bolometric correction can be obtained via the simple power-law scaling by Netzer (2019),
, for which we apply the conversions of Kozłowski (2015). To estimate the bolometric luminosity, the corresponding bolometric correction can be obtained via the simple power-law scaling by Netzer (2019), ![${\kappa }_{\mathrm{bol}}=25\times {[{L}_{3000}/{10}^{42}\mathrm{erg}{{\rm{s}}}^{-1}]}^{-0.2}\sim 3.36$](https://content.cld.iop.org/journals/0004-637X/912/1/10/revision2/apjabe9b2ieqn35.gif) , which yields Lbol = 3.36L3000 ∼ 7.68 × 1046 erg s−1. The Eddington limit can be estimated for M• ≃ 2 × 109
M⊙, which was obtained via the SED fitting as well as the virial mass using the line dispersion, LEdd ≃ 2.5 × 1047 × (M•/(2 × 109
M⊙)) erg s−1. Finally, the Eddington ratio is η = Lbol/LEdd ∼ 0.31, which is about a factor of two smaller than the Eddington ratio of 0.58 obtained by Sredzińska et al. (2017) using the SED fitting. Still, the source is highly accreting, with η comparable to HE 0413-4031 (η = 0.4, Zajaček et al. 2020).
, which yields Lbol = 3.36L3000 ∼ 7.68 × 1046 erg s−1. The Eddington limit can be estimated for M• ≃ 2 × 109
M⊙, which was obtained via the SED fitting as well as the virial mass using the line dispersion, LEdd ≃ 2.5 × 1047 × (M•/(2 × 109
M⊙)) erg s−1. Finally, the Eddington ratio is η = Lbol/LEdd ∼ 0.31, which is about a factor of two smaller than the Eddington ratio of 0.58 obtained by Sredzińska et al. (2017) using the SED fitting. Still, the source is highly accreting, with η comparable to HE 0413-4031 (η = 0.4, Zajaček et al. 2020).
The highly accreting sources exhibit the largest scatter with respect to the standard RL relation, with a trend of shorter time delays by a factor of a few than expected based on their monochromatic luminosity. This was studied for the Hβ reverberation-mapped sources (Du et al. 2015, 2016; Martínez-Aldama et al. 2019), and confirmed for the higher-redshift Mg ii reverberation-mapped sources as well (Homayouni et al. 2020; Martínez-Aldama et al. 2020; Zajaček et al. 2020), which suggests a common mechanism for time-delay shortening driven by the accretion rate. The relation between the rest-frame time delay of the Hβ line and the linear combination of the monochromatic luminosity at 5100 Å and the relative strength of the Fe II line (flux ratio between Fe II and Hβ lines) yields a low scatter of only σrms = 0.196 dex (Du & Wang 2019), which suggests that the relative Fe II strength and hence the accretion rate can account for most of the scatter.
In addition, highly accreting Mg ii reverberation-mapped sources exhibit a generally lower scatter along the multidimensional RL relations (Martínez-Aldama et al. 2020). This motivates us to further study how high-luminosity and highly accreting sources such as HE 0435-4312 affect the scatter along the radius–luminosity relation on their own as well as in combination with independent observables, such as the Mg ii line FWHM, the Fe II strength RFe II , and the fractional variability Fvar of the continuum, where the latter two parameters are correlated with the accretion rate.
4.3. Position in the Radius–Luminosity Plane
The high luminosity of HE 0435-4312 is expected to be beneficial for constraining the Mg ii-based radius–luminosity relation. We add HE 0435-4312 to the original sample of 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020). To characterize the accretion rate of our source and in order to compare it with other sources, we make use of the dimensionless accretion rate  expressed specifically for 3000 Å as (Wang et al. 2014; Martínez-Aldama et al. 2020)
expressed specifically for 3000 Å as (Wang et al. 2014; Martínez-Aldama et al. 2020)
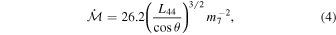
where L44 is the luminosity at 3000 Å expressed in units of 1044 erg s−1 and m7 is the central black hole mass expressed in units of 107
M⊙. The angle θ is the inclination angle with respect to the accretion disk and we set  , which represents the mean inclination angle for type I AGNs according to studies of the covering factor of the dusty torus (see, e.g., Lawrence & Elvis 2010; Ichikawa et al. 2015).
, which represents the mean inclination angle for type I AGNs according to studies of the covering factor of the dusty torus (see, e.g., Lawrence & Elvis 2010; Ichikawa et al. 2015).
Using Equation (4) and the estimate of black hole mass based on the line dispersion in the mean spectrum and the broadband SED fitting, we obtain  or
or  for HE 0435-4312, which puts it into the high-accretor category according to Martínez-Aldama et al. (2020), where all the Mg ii reverberation-mapped sources with
for HE 0435-4312, which puts it into the high-accretor category according to Martínez-Aldama et al. (2020), where all the Mg ii reverberation-mapped sources with  belong (median value of their Mg ii sample). Using the smaller SMBH mass based on Mg ii FWHM in the mean spectrum yields a larger
belong (median value of their Mg ii sample). Using the smaller SMBH mass based on Mg ii FWHM in the mean spectrum yields a larger  by a factor of a few,
by a factor of a few,  (based on fMR) and
(based on fMR) and  (based on fWoo). In the further analysis, we adopt the
(based on fWoo). In the further analysis, we adopt the  value based on the line dispersion in the mean spectrum because of the consistency of
value based on the line dispersion in the mean spectrum because of the consistency of  with the SMBH mass inferred from the broadband fitting of Sredzińska et al. (2017). In Figure 4 (left panel), we plot the RL relation for all 69 sources including HE 0435-4312 (green circle). In the right panel of Figure 4, we restrict the RL relation to only highly accreting sources, which results in a significantly reduced rms scatter of σrms = 0.1991 dex versus σrms = 0.2994 dex for the full sample. Adding HE 0435-4312 results in a small but detectable reduction of scatter for both the full sample (0.2994 versus 0.3014) and the highly accreting subsample (0.1991 versus 0.2012) with respect to the original Mg ii sample of 68 sources (Martínez-Aldama et al. 2020).
with the SMBH mass inferred from the broadband fitting of Sredzińska et al. (2017). In Figure 4 (left panel), we plot the RL relation for all 69 sources including HE 0435-4312 (green circle). In the right panel of Figure 4, we restrict the RL relation to only highly accreting sources, which results in a significantly reduced rms scatter of σrms = 0.1991 dex versus σrms = 0.2994 dex for the full sample. Adding HE 0435-4312 results in a small but detectable reduction of scatter for both the full sample (0.2994 versus 0.3014) and the highly accreting subsample (0.1991 versus 0.2012) with respect to the original Mg ii sample of 68 sources (Martínez-Aldama et al. 2020).
Figure 4. Left panel: Mg ii-based radius–luminosity relation including all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and the new source HE 0435-4312 denoted by a green circle. The relative UV Fe II strength RFe II
is color-coded for each source according to the color axis on the right (except for NGC 4151 and CTS 252, for which RFe II
was not available, and these sources are denoted by empty circles). For HE 0435-4312, we obtained RFe II
= EW(Fe II)/EW(Mg II) ∼ 2.36. Right panel: the same as the left panel, but for highly accreting sources with  , where the division of high accretors was taken from Martínez-Aldama et al. (2020) according to the median value of their full sample. The scatter along the RL relation is noticeably lower for high accretors than for the full sample. In both panels, dashed and dotted lines denote the 68% and 95% confidence intervals, respectively.
, where the division of high accretors was taken from Martínez-Aldama et al. (2020) according to the median value of their full sample. The scatter along the RL relation is noticeably lower for high accretors than for the full sample. In both panels, dashed and dotted lines denote the 68% and 95% confidence intervals, respectively.
Download figure:
Standard image High-resolution imageIn the extended RL relations that include other independent observables in the linear combination of logarithms, namely Mg ii line FWHM, the relative Fe II strength with respect to the Mg ii line RFe II , and the continuum fractional variability Fvar, HE 0435-4312 lies within 1σ of the mean relation for both the full sample and the highly accreting subsample; see Figure 5 for the combination with FWHM, Figure 6 that includes RFe II , and Figure 7 that utilizes the continuum Fvar. When one restricts the analysis to the highly accreting subsample, the rms scatter drops below 0.2 dex in all combinations, with the smallest scatter exhibited by the RL relation including RFe II (σrms = 0.1734 dex). In Table 2, we summarize the best-fit parameters as well as the rms scatter for all the RL relations for the highly accreting subsample including HE 0435-4312. Our high-luminosity source is beneficial for the reduction of rms scatter, except for the combination including RFe II , where the rms scatter marginally increases in comparison with the best-fit result of Martínez-Aldama et al. (2020). For all RL relations, adding the new quasar leads to an increase in the Pearson correlation coefficient. For the comparison of the rms scatter and the correlation coefficients with and without the inclusion of HE 0435-4312, see the last four columns of Table 2.
Figure 5. Rest-frame time delay expressed as a function of  and
and  . Left panel: the linear combination studied for all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and a new source HE 0435-4312 denoted by a green circle. Right panel: as in Figure 4, the linear combination is restricted to highly accreting sources with the same division according to
. Left panel: the linear combination studied for all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and a new source HE 0435-4312 denoted by a green circle. Right panel: as in Figure 4, the linear combination is restricted to highly accreting sources with the same division according to  . In both panels, each source is color-coded according to the corresponding Mg ii FWHM.
. In both panels, each source is color-coded according to the corresponding Mg ii FWHM.
Download figure:
Standard image High-resolution imageFigure 6. Rest-frame time delay expressed as a function of  and
and  . Left panel: the linear combination studied for all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and a new source HE 0435-4312 denoted by a green circle. Right panel: as in Figure 4, the linear combination is restricted to highly accreting sources with the same division according to
. Left panel: the linear combination studied for all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and a new source HE 0435-4312 denoted by a green circle. Right panel: as in Figure 4, the linear combination is restricted to highly accreting sources with the same division according to  . In both panels, each source is color-coded according to the corresponding relative UV Fe II strength RFe II
.
. In both panels, each source is color-coded according to the corresponding relative UV Fe II strength RFe II
.
Download figure:
Standard image High-resolution imageFigure 7. Rest-frame time delay expressed as a function of  and
and  . Left panel: the linear combination studied for all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and a new source HE 0435-4312 denoted by a green circle. Right panel: as in Figure 4, the linear combination is restricted to highly accreting sources with the same division according to
. Left panel: the linear combination studied for all 68 Mg ii reverberation-mapped sources studied in Martínez-Aldama et al. (2020) and a new source HE 0435-4312 denoted by a green circle. Right panel: as in Figure 4, the linear combination is restricted to highly accreting sources with the same division according to  . In both panels, each source is color-coded according to the corresponding continuum fractional variability Fvar.
. In both panels, each source is color-coded according to the corresponding continuum fractional variability Fvar.
Download figure:
Standard image High-resolution imageTable 2. Parameters for The Standard RL Relation as Well as Multidimensional RL Relations Including Independent Observables, Namely FWHM, RFe II , and Fvar, for the Highly Accreting Subsample (35 Sources Including HE 0435-4312)

| K1 | K2 | K3 | σrms [dex] | r | σrms [dex] (without) | r (without) |
|---|---|---|---|---|---|---|---|

| 0.422 ± 0.055 | 1.374 ± 0.082 | ⋯ | 0.1991 | 0.80 | 0.2012 | 0.78 |

| 0.43 ± 0.06 | −0.13 ± 0.31 | 1.44 ± 0.17 | 0.1986 | 0.80 | 0.2007 | 0.78 |

| 0.45 ± 0.05 | 0.84 ± 0.29 | 1.28 ± 0.08 | 0.1734 | 0.85 | 0.1718 | 0.84 |

| 0.39 ± 0.06 | −0.38 ± 0.18 | 0.99 ± 0.19 | 0.1861 | 0.83 | 0.1863 | 0.82 |
Note. The last four columns show rms scatter and Pearson's correlation coefficient with and without HE 0435-4312 for comparison.
Download table as: ASCIITypeset image
The dimensionless accretion rate  of Mg ii sources defined by Equation (4) is intrinsically correlated with the rest-frame time delay via the black hole mass (
of Mg ii sources defined by Equation (4) is intrinsically correlated with the rest-frame time delay via the black hole mass ( , while the Eddington ratio η ∝ τ−1) as discussed by Martínez-Aldama et al. (2020). Therefore we do not use
, while the Eddington ratio η ∝ τ−1) as discussed by Martínez-Aldama et al. (2020). Therefore we do not use  in extended RL relations, because the correlation would be artificially enhanced. We merely use
in extended RL relations, because the correlation would be artificially enhanced. We merely use  for the division of the sample into the high and low accretors. For the extended RL relations, we prefer the independent observables Mg ii FWHM, UV RFe II
, and Fvar. Characterizing the accretion-rate intensity by
for the division of the sample into the high and low accretors. For the extended RL relations, we prefer the independent observables Mg ii FWHM, UV RFe II
, and Fvar. Characterizing the accretion-rate intensity by  is justified by its correlation with the relative UV Fe II strength RFe II
, which in turn is related to the accretion rate (Dong et al. 2011; Martínez-Aldama et al. 2020), which was analogously shown for optical Fe II strength (Shen & Ho 2014; Du & Wang 2019). For the whole sample of Mg ii sources, including HE 0435-4312, for which RFe II
can be estimated (in total 66 sources), the Spearman correlation coefficient between
is justified by its correlation with the relative UV Fe II strength RFe II
, which in turn is related to the accretion rate (Dong et al. 2011; Martínez-Aldama et al. 2020), which was analogously shown for optical Fe II strength (Shen & Ho 2014; Du & Wang 2019). For the whole sample of Mg ii sources, including HE 0435-4312, for which RFe II
can be estimated (in total 66 sources), the Spearman correlation coefficient between  and RFe II
is positive with ρ = 0.440 (with a p-value of 2.19 × 10−4). For the same sample, the relative Fe II strength is in turn positively correlated with the Eddington ratio η = Lbol/LEdd with ρ = 0.447 (p = 1.71 × 10−4). This justifies the division into low and high accretors according to
and RFe II
is positive with ρ = 0.440 (with a p-value of 2.19 × 10−4). For the same sample, the relative Fe II strength is in turn positively correlated with the Eddington ratio η = Lbol/LEdd with ρ = 0.447 (p = 1.71 × 10−4). This justifies the division into low and high accretors according to  .
.
On the other hand,  is anticorrelated with respect to the continuum variability Fvar with ρ = −0.480 (p = 2.97 × 10−5, 69 sources). Furthermore, the parameter
is anticorrelated with respect to the continuum variability Fvar with ρ = −0.480 (p = 2.97 × 10−5, 69 sources). Furthermore, the parameter  is anticorrelated with Mg ii FWHM, although the (anti)correlation is weaker than for RFe II
and Fvar with ρ = −0.386 (p = 1.05 × 10−3, 69 sources). The anticorrelation between Mg ii FWHM and
is anticorrelated with Mg ii FWHM, although the (anti)correlation is weaker than for RFe II
and Fvar with ρ = −0.386 (p = 1.05 × 10−3, 69 sources). The anticorrelation between Mg ii FWHM and  , and hence also RFe II
, is expected from optical studies of eigenvector 1 of the quasar main sequence (Boroson & Green 1992; Sulentic et al. 2000), which can be traced in the UV plane as well (Kozłowski et al. 2020). These (anti)correlations between
, and hence also RFe II
, is expected from optical studies of eigenvector 1 of the quasar main sequence (Boroson & Green 1992; Sulentic et al. 2000), which can be traced in the UV plane as well (Kozłowski et al. 2020). These (anti)correlations between  and other quantities across classical and extended RL relations are also apparent in the color-coded plots in Figures 4–7. The reduction in scatter for the high-
and other quantities across classical and extended RL relations are also apparent in the color-coded plots in Figures 4–7. The reduction in scatter for the high- subsample could therefore arise due to a lower variability and the stabilisation of the luminosity and black hole mass ratio for the sources accreting close to the Eddington limit as discussed in detail in Martínez-Aldama et al. (2020); see also Ai et al. (2010) and Marziani & Sulentic (2014).
subsample could therefore arise due to a lower variability and the stabilisation of the luminosity and black hole mass ratio for the sources accreting close to the Eddington limit as discussed in detail in Martínez-Aldama et al. (2020); see also Ai et al. (2010) and Marziani & Sulentic (2014).
In order to clarify our idea of the sample division quantitatively, we divided the sample analyzed by Martínez-Aldama et al. (2020), with the studied source HE 0435-4312 included, considering the median values of RFe II
and Fvar ( ,
,  ) instead of
) instead of  (
( ). Since the correlation between
). Since the correlation between  and RFe II
is positive, we expect that the high Fe II emitters show the highest
and RFe II
is positive, we expect that the high Fe II emitters show the highest  values, i.e., above the corresponding median value. On the other hand, the correlation between Fvar and
values, i.e., above the corresponding median value. On the other hand, the correlation between Fvar and  is negative, hence highly accreting AGNs show a lower variability or Fvar values with respect to the median value of each parameter. In the case of the
is negative, hence highly accreting AGNs show a lower variability or Fvar values with respect to the median value of each parameter. In the case of the  –RFe II
correlation, we find that ∼70% of the sample satisfies the criteria with respect to the median values of RFe II
and
–RFe II
correlation, we find that ∼70% of the sample satisfies the criteria with respect to the median values of RFe II
and  . Meanwhile, for the
. Meanwhile, for the  –Fvar correlation, ∼72% of our sources are within the median values considered. This is graphically shown in Figure 8, where we depict the correlation
–Fvar correlation, ∼72% of our sources are within the median values considered. This is graphically shown in Figure 8, where we depict the correlation  –RFe II
(left panel) and the anticorrelation
–RFe II
(left panel) and the anticorrelation  –Fvar (right panel) for the studied sample of Mg ii sources. Therefore, we can conclude that the division into low and high accretors based on
–Fvar (right panel) for the studied sample of Mg ii sources. Therefore, we can conclude that the division into low and high accretors based on  is analogous to a division based on the independent parameters RFe II
and Fvar. To illustrate this, in Figure 4 we use RFe II
for color-coding individual sources in the RL relation for the whole sample (left panel) and the high-accretor subsample (right panel).
is analogous to a division based on the independent parameters RFe II
and Fvar. To illustrate this, in Figure 4 we use RFe II
for color-coding individual sources in the RL relation for the whole sample (left panel) and the high-accretor subsample (right panel).
Figure 8. Relation between the dimensionless accretion rate  and the relative UV Fe II strength RFe II
and the continuum fractional variability Fvar. Left panel: the positive correlation between
and the relative UV Fe II strength RFe II
and the continuum fractional variability Fvar. Left panel: the positive correlation between  and RFe II
(Spearman correlation coefficient ρ = 0.44; p = 2.2 × 10−4). The dashed lines mark the median values of each parameter. When the sample is divided according to the median of RFe II
, ∼ 70% of high-/low-
and RFe II
(Spearman correlation coefficient ρ = 0.44; p = 2.2 × 10−4). The dashed lines mark the median values of each parameter. When the sample is divided according to the median of RFe II
, ∼ 70% of high-/low- sources are present. The star symbol marks HE 0435-4312. Right panel: the anticorrelation between
sources are present. The star symbol marks HE 0435-4312. Right panel: the anticorrelation between  and Fvar (Spearman correlation coefficient ρ = −0.48; p = 2.9 × 10−5). The dashed lines mark the median values of each parameter. When the Mg ii sample is divided according to the median value of Fvar, ∼72% of high-/low-
and Fvar (Spearman correlation coefficient ρ = −0.48; p = 2.9 × 10−5). The dashed lines mark the median values of each parameter. When the Mg ii sample is divided according to the median value of Fvar, ∼72% of high-/low- sources are included. The star symbol depicts HE 0435-4312.
sources are included. The star symbol depicts HE 0435-4312.
Download figure:
Standard image High-resolution image5. Discussion
By combining the SALT spectroscopy and the photometric data from more instruments, we were able to determine the rest-frame time delay of  days between the Mg ii broad line and the underlying continuum at 3000 Å. Fitting the Mg ii line with the underlying continuum and Fe II pseudocontinuum is rather complex, but we show in Appendix B that the time-delay distribution for a different Fe II template is comparable and does not affect the main time-delay analysis presented in this paper.
days between the Mg ii broad line and the underlying continuum at 3000 Å. Fitting the Mg ii line with the underlying continuum and Fe II pseudocontinuum is rather complex, but we show in Appendix B that the time-delay distribution for a different Fe II template is comparable and does not affect the main time-delay analysis presented in this paper.
The rest-frame time delay is essentially the same as for another luminous and highly accreting quasar, HE 0413-4031, analyzed in Zajaček et al. (2020). While the RL relation for the collected sample of 69 Mg ii reverberation-mapped sources has a relatively large scatter of ∼0.3 dex, it is significantly reduced to 0.2 dex when we consider only high accretors, where HE 0435-4312 also belongs with an Eddington ratio of ∼0.31–0.58 (the corresponding dimensionless accretion rate is  ). Further reduction of the scatter is achieved in the 3D RL relations that include independent observables (FWHM, RFe II
, and Fvar). Especially, the linear combination including the relative strength of Fe II leads to the smallest scatter of 0.17 dex. Because of the correlation between RFe II
and
). Further reduction of the scatter is achieved in the 3D RL relations that include independent observables (FWHM, RFe II
, and Fvar). Especially, the linear combination including the relative strength of Fe II leads to the smallest scatter of 0.17 dex. Because of the correlation between RFe II
and  (Martínez-Aldama et al. 2020), this indicates that the scatter along the RL relation is driven by the accretion rate, as we already showed in Zajaček et al. (2020) for a sample of only 11 Mg ii sources.
(Martínez-Aldama et al. 2020), this indicates that the scatter along the RL relation is driven by the accretion rate, as we already showed in Zajaček et al. (2020) for a sample of only 11 Mg ii sources.
In the following subsection, we further discuss some aspects of the Mg ii variability, focusing on the interpretation of a relatively large variability of the Mg ii line for our source. Then, using the sample of 35 high accretors that exhibit a small scatter along the RL relation, we show how it is possible to apply the radius–luminosity relation to constrain cosmological parameters.
5.1. Variability of Mg ii Emission
The fractional variability of the Mg ii line of HE 0435-4312 is  (excluding observation 19). The continuum fractional variability is larger,
(excluding observation 19). The continuum fractional variability is larger,  over 14.74 yr. However, when the continuum light curve is separated into the first 7 yr (CATALINA),
over 14.74 yr. However, when the continuum light curve is separated into the first 7 yr (CATALINA),  , and the last 6 yr (SALT monitoring),
, and the last 6 yr (SALT monitoring),  , then both values are comparable to the fractional variability of Mg ii emission. This implies that Mg ii-emitting clouds reprocess the continuum emission very well for our source. In other words, the triggering continuum and a line echo have similar amplitudes, suggesting that sharp echoes are present and that the Mg ii-emitting region lies on (or close to) an isodelay surface, which is an important geometrical condition. In addition, the variability timescale of the continuum must be long enough, i.e., longer than the light-travel time through the locally optimally emitting cloud (LOC) model of the BLR. It seems that both conditions are fulfilled for our source.
, then both values are comparable to the fractional variability of Mg ii emission. This implies that Mg ii-emitting clouds reprocess the continuum emission very well for our source. In other words, the triggering continuum and a line echo have similar amplitudes, suggesting that sharp echoes are present and that the Mg ii-emitting region lies on (or close to) an isodelay surface, which is an important geometrical condition. In addition, the variability timescale of the continuum must be long enough, i.e., longer than the light-travel time through the locally optimally emitting cloud (LOC) model of the BLR. It seems that both conditions are fulfilled for our source.
This is in contrast with the study of Guo et al. (2020), who used the CLOUDY code and the LOC model to study the response of Mg ii emission to the variable continuum. They found that at the Eddington ratio of ∼0.4, the Mg ii emission saturates and does not further increase with the rise in the continuum luminosity. Observationally, Yang et al. (2020) found for extreme-variability quasars that Mg ii emission responds to the continuum but with a smaller amplitude,  . Although our source has a high Eddington ratio comparable to that studied in Guo et al. (2020), η ∼ 0.3–0.6, its Mg ii emission responds very efficiently to the variable continuum. For the previous highly accreting luminous quasar HE 0413-4031 that we studied (Zajaček et al. 2020), we also showed that the Mg ii line can respond strongly to the increase in the continuum,
. Although our source has a high Eddington ratio comparable to that studied in Guo et al. (2020), η ∼ 0.3–0.6, its Mg ii emission responds very efficiently to the variable continuum. For the previous highly accreting luminous quasar HE 0413-4031 that we studied (Zajaček et al. 2020), we also showed that the Mg ii line can respond strongly to the increase in the continuum,  , as shown by the intrinsic Baldwin effect.
, as shown by the intrinsic Baldwin effect.
A possible interpretation of the discrepancy between the saturation of Mg ii emission at larger Eddington ratios modeled nominally by Guo et al. (2020) and our two highly accreting sources, HE 0435-4312 and HE 0413-4031, which exhibit a strong response of the Mg ii emission to the continuum, is an order-of-magnitude difference in the black hole mass as well as in the studied luminosity at 3000 Å. In Guo et al. (2020), they used M• = 108 M⊙ and L3000 = 1044–1045 erg s−1 as well as (Rout, Γ) = (1017.5, −2) for the outer radius and the slope of the LOC model, respectively. For our source, all of the characteristic parameters are increased: M• ≃ 2 × 109 M⊙, L3000 ≃ 1046.36 erg s−1, and RMg II = 1017.9 cm. Mainly the larger outer radius implies that not all of the Mg ii-emitting gas is fully ionized at these scales and can exhibit "partial breathing," as is also shown by Guo et al. (2020) for the case with Rout = 1018 cm, when the Mg ii line luminosity continues to rise with the increase in the continuum luminosity.
5.2. Constraining Cosmological Parameters Using an Mg ii Highly Accreting Subsample
Since the RL relation for a highly accreting Mg ii subsample showed a relatively small scatter of ∼0.2 dex, we attempt to use it for cosmological purposes. We adopt the general approach outlined in Martínez-Aldama et al. (2019), that is we assume a perfect relation between the absolute luminosity and the measured time delay, and having absolute luminosity and the observed flux we can determine the luminosity distance for each source. We do not use here the best-fit relation given in Figure 4, right panel, since this relation was calibrated for a specific assumed cosmology. Therefore we assume a relation in a general form,
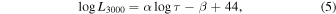
and we treat α and β as free parameters. We consider first the case of a flat cosmology, and we assume the value of the Hubble constant H0 = 67.36 km s−1 Mpc−1 adopted from Planck Collaboration et al. (2020), and we minimize the fits to the predicted luminosity distance by varying Ωm, α, and β. The preliminary fit was highly unsatisfactory, and we used a sigma-clipping method to remove the outliers (eight sources). The final sample was well fitted with the standard ΛCDM model for  (1σ error). This result is fully consistent with the data from Planck Collaboration et al. (2020) with
(1σ error). This result is fully consistent with the data from Planck Collaboration et al. (2020) with  . The values obtained for the remaining two parameters were α = 1.8 and β = 2.1, which would correspond to a slightly different RL relation,
. The values obtained for the remaining two parameters were α = 1.8 and β = 2.1, which would correspond to a slightly different RL relation,  . The results are illustrated in Figure 9, left panel. We also attempted to constrain both ΩΛ and Ωm, waiving the assumption of a flat space. The parameters α and β in Equation (5) were kept fixed to the values inferred from the flat-cosmology fit, i.e., α = 1.8 and β = 2.1. The result is given in the right panel of Figure 9. The best fit in this case implies a slightly lower Ωm, but the contour error is large and covers the best fit from Planck Collaboration et al. (2020) within the 1σ confidence level. The data do not yet tightly constrain the cosmological parameters, but the Mg ii highly accreting subsample does not imply any departures from the standard model, and the data quality is much higher, and constrains the parameters better than the larger sample based on the Hβ line and discussed in Martínez-Aldama et al. (2019), and somewhat better than the mixed sample discussed in Czerny et al. (2020).
. The results are illustrated in Figure 9, left panel. We also attempted to constrain both ΩΛ and Ωm, waiving the assumption of a flat space. The parameters α and β in Equation (5) were kept fixed to the values inferred from the flat-cosmology fit, i.e., α = 1.8 and β = 2.1. The result is given in the right panel of Figure 9. The best fit in this case implies a slightly lower Ωm, but the contour error is large and covers the best fit from Planck Collaboration et al. (2020) within the 1σ confidence level. The data do not yet tightly constrain the cosmological parameters, but the Mg ii highly accreting subsample does not imply any departures from the standard model, and the data quality is much higher, and constrains the parameters better than the larger sample based on the Hβ line and discussed in Martínez-Aldama et al. (2019), and somewhat better than the mixed sample discussed in Czerny et al. (2020).
Figure 9. Constraining cosmological parameters using the highly accreting subsample of Mg ii reverberation-mapped sources, including HE 0435-4312. Left panel: the quasar Hubble diagram using 27 sources (red points), after removal of eight outliers, with the best-fit standard ΛCDM model (black solid line;  with fixed H0 = 67.36 km s−1 Mpc−1 according to Planck Collaboration et al. 2020). The bottom panel shows the residuals
with fixed H0 = 67.36 km s−1 Mpc−1 according to Planck Collaboration et al. 2020). The bottom panel shows the residuals  , where
, where  is the expected luminosity distance and DL is the measured one. HE 0435-4312 is marked by a black circle. Right panel: contour plot showing the confidence levels at 68% (orange) and 95% (brown) for the general ΛCDM model based on χ2 fitting. The yellow star depicts the best-fit (Ωm, ΩΛ) = (0.19, 0.62) and the blue filled circle shows the cosmological constraints as provided by Planck Collaboration et al. (2020).
is the expected luminosity distance and DL is the measured one. HE 0435-4312 is marked by a black circle. Right panel: contour plot showing the confidence levels at 68% (orange) and 95% (brown) for the general ΛCDM model based on χ2 fitting. The yellow star depicts the best-fit (Ωm, ΩΛ) = (0.19, 0.62) and the blue filled circle shows the cosmological constraints as provided by Planck Collaboration et al. (2020).
Download figure:
Standard image High-resolution image6. Conclusions
Our main conclusions from the reverberation mapping analysis of the source HE 0435-4312 (z = 1.2231, ![$\mathrm{log}({L}_{3000}[\mathrm{erg}\,{{\rm{s}}}^{-1}])={46.359}_{-0.034}^{+0.038}$](https://content.cld.iop.org/journals/0004-637X/912/1/10/revision2/apjabe9b2ieqn106.gif) ) can be summarized as follows.
) can be summarized as follows.
- 1.Using seven different methods, we determined the mean rest-frame time delay of
 days, with all the methods giving a consistent time-delay peak within uncertainties that were determined using the bootstrap or the maximum-likelihood method. By combining the bootstrap method, the weighting by the number of overlapping data points, and the analysis of mock light curves, we could classify the other prominent time-delay peaks as artifacts due to the particular sampling and a limited observational duration.
days, with all the methods giving a consistent time-delay peak within uncertainties that were determined using the bootstrap or the maximum-likelihood method. By combining the bootstrap method, the weighting by the number of overlapping data points, and the analysis of mock light curves, we could classify the other prominent time-delay peaks as artifacts due to the particular sampling and a limited observational duration. - 2.The fractional variability of Mg ii emission (∼5.4%) is comparable to the continuum variability, hence the Mg ii line flux for our source has not reached the saturation level despite the high Eddington ratio of ∼0.3–0.6. This is most likely due to the large black hole mass of ∼2 × 109 M⊙ and the large extent of the Mg ii-emitting region, RMg II = 1017.9 cm.
- 3.The large luminosity of HE 0435-4312 is beneficial for decreasing the scatter and increasing the correlation coefficient for the Mg ii-based radius–luminosity relation. The scatter is ∼0.2 dex for the highly accreting subsample of Mg ii sources, where HE 0435-4312 belongs. A further reduction in the scatter is achieved using linear combinations with independent observables (FWHM, relative Fe II strength, and fractional variability), which indicates that the scatter along the radius–luminosity relation is mainly driven by the accretion rate.
- 4.A low scatter of the radius–luminosity relation for the highly accreting subsample motivates us to apply these sources for constraining cosmological parameters. Given the current number of sources (27, after removal of eight outliers) and the data quality, the best-fit values of the cosmological parameters (Ωm, ΩΛ) = (0.19; 0.62) are consistent with the standard cosmological model within the 1σ confidence level.
The project is based on observations made with the SALT under programs 2012-2-POL-003, 2013-1-POL-RSA-002, 2013-2-POL-RSA-001, 2014-1-POL-RSA-001, 2014-2-SCI-004, 2015-1-SCI-006, 2015-2-SCI-017, 2016-1-SCI-011, 2016-2-SCI-024, 2017-1-SCI-009, 2017-2-SCI-033, 2018-1-MLT-004 (PI: B. Czerny). The authors acknowledge the financial support by the National Science Centre, Poland, grant No. 2017/26/A/ST9/00756 (Maestro 9), and by the Ministry of Science and Higher Education (MNiSW) grant DIR/WK/2018/12. G.P. acknowledges the grant MNiSW DIR/WK/2018/09. K.H. acknowledges support by the Polish National Science Centre grant 2015/18/E/ST9/00580. M.Z. was supported by the NAWA under the agreement PPN/WYM/2019/1/00064 to perform a three-month exchange stay at the Charles University and the Astronomical Institute of the Czech Academy of Sciences in Prague. M.H. and C.S.F. are supported by Deutsche Forschungsgemeinschaft grants CH71/33 and CH71/34. The OGLE project has received funding from the National Science Centre, Poland, grant MAESTRO 2014/14/A/ST9/00121. The Polish participation in SALT is funded by grant No. MNiSW DIR/WK/2016/07. M.Z., V.K., and B.C. acknowledge PPN/BCZ/2019/1/00069 (MŠMT 8J20PL037) for the support of the Polish-Czech mobility program. This paper uses observations made at the South African Astronomical Observatory (SAAO).
Software: IRAF (Tody 1986, 1993), JAVELIN (Zu et al. 2011, 2013, 2016), PyCCF (Sun et al. 2018), vnrm.py (Chelouche et al. 2017), zdcf_v2.f90 (Alexander 1997), plike_v4.f90 (Alexander 1997), delay_chi2.f (Czerny et al. 2013), sklearn (Pedregosa et al. 2011), statsmodels (Seabold & Perktold 2010), numpy (Oliphant 2015), matplotlib (Hunter 2007).
Appendix A: Photometric and Spectroscopic Data
Continuum magnitudes with uncertainties are shown in Table 3.
Table 3. Continuum Magnitudes with Uncertainties
| JD | Magnitude (V band) | Error | Instrument |
|---|---|---|---|
| − 2,450,000 | [mag] | [mag] | No. |
| 3696.98828 | 16.8733330 | 2.51584481E-02 | 1 |
| 4067.76562 | 16.9422932 | 1.88624337E-02 | 1 |
| 4450.48828 | 16.9090614 | 2.42404137E-02 | 1 |
| 4837.18359 | 17.0258694 | 1.94998924E-02 | 1 |
| 5190.14453 | 17.0322189 | 2.00808570E-02 | 1 |
| 5564.26562 | 16.9177780 | 2.75434572E-02 | 1 |
| 5889.63672 | 16.8666668 | 2.98607871E-02 | 1 |
| 6296.05078 | 16.9212513 | 2.82704569E-02 | 1 |
| 6893.60449 | 17.1165180 | 1.20000001E-02 | 2 |
| 6986.31592 | 17.1647282 | 1.20000001E-02 | 2 |
| 7032.45020 | 17.1936970 | 1.20000001E-02 | 2 |
| 7035.63428 | 17.1329994 | 4.00000019E-03 | 3 |
| 7047.64209 | 17.1079998 | 4.00000019E-03 | 3 |
| 7058.61475 | 17.1240005 | 8.00000038E-03 | 3 |
| 7083.54346 | 17.1119995 | 4.99999989E-03 | 3 |
| 7116.50684 | 17.1089993 | 8.00000038E-03 | 3 |
| 7253.89209 | 17.1749992 | 4.00000019E-03 | 3 |
| 7261.88330 | 17.1779995 | 4.00000019E-03 | 3 |
| 7267.91504 | 17.1630001 | 4.99999989E-03 | 3 |
| 7273.84717 | 17.1849995 | 4.99999989E-03 | 3 |
| 7283.84912 | 17.1779995 | 4.00000019E-03 | 3 |
| 7295.84277 | 17.1889992 | 6.00000005E-03 | 3 |
| 7306.78125 | 17.1690006 | 4.00000019E-03 | 3 |
| 7317.74023 | 17.1889992 | 4.99999989E-03 | 3 |
| 7327.77490 | 17.1959991 | 6.00000005E-03 | 3 |
| 7340.70654 | 17.2140007 | 4.00000019E-03 | 3 |
| 7355.69482 | 17.1860008 | 4.99999989E-03 | 3 |
| 7363.66650 | 17.2159996 | 4.00000019E-03 | 3 |
| 7364.53760 | 17.2753944 | 1.20000001E-02 | 2 |
| 7374.70947 | 17.2080002 | 4.00000019E-03 | 3 |
| 7385.55762 | 17.2049999 | 4.00000019E-03 | 3 |
| 7398.61768 | 17.2269993 | 4.00000019E-03 | 3 |
| 7415.58545 | 17.2229996 | 4.00000019E-03 | 3 |
| 7426.56641 | 17.2010002 | 4.00000019E-03 | 3 |
| 7436.52539 | 17.2049999 | 4.99999989E-03 | 3 |
| 7447.52783 | 17.2080002 | 4.00000019E-03 | 3 |
| 7457.52246 | 17.2089996 | 4.00000019E-03 | 3 |
| 7655.49414 | 17.1270580 | 1.20000001E-02 | 2 |
| 7692.38037 | 17.1313496 | 1.20000001E-02 | 2 |
| 7717.70557 | 17.1089993 | 4.00000019E-03 | 3 |
| 7754.46582 | 17.0703278 | 1.20000001E-02 | 2 |
| 7803.32959 | 17.1150951 | 1.20000001E-02 | 2 |
| 7973.91357 | 17.2000008 | 1.30000003E-02 | 3 |
| 7984.59424 | 17.2056389 | 1.20000001E-02 | 2 |
| 8038.86182 | 17.1779995 | 6.00000005E-03 | 3 |
| 8091.25000 | 17.2399998 | 9.99999978E-03 | 4 |
| 8102.25000 | 17.2199993 | 4.00000019E-03 | 4 |
| 8104.25000 | 17.2430000 | 8.99999961E-03 | 4 |
| 8105.00000 | 17.2430000 | 4.99999989E-03 | 4 |
| 8107.25000 | 17.2509995 | 6.00000005E-03 | 4 |
| 8112.48926 | 17.2262497 | 1.20000001E-02 | 2 |
| 8130.25000 | 17.2639999 | 8.99999961E-03 | 4 |
| 8138.00000 | 17.2459984 | 7.00000022E-03 | 4 |
| 8147.00000 | 17.2319984 | 8.00000038E-03 | 4 |
| 8166.00000 | 17.2319984 | 2.00000009E-03 | 4 |
| 8182.00000 | 17.2519989 | 8.00000038E-03 | 4 |
| 8206.00000 | 17.2309990 | 8.99999961E-03 | 4 |
| 8410.25000 | 17.1949997 | 8.99999961E-03 | 4 |
| 8540.00000 | 17.2019997 | 8.00000038E-03 | 4 |
| 8568.24609 | 17.1906471 | 1.20000001E-02 | 2 |
| 8585.50000 | 17.2489986 | 8.00000038E-03 | 4 |
| 8775.75000 | 17.1980000 | 7.00000022E-03 | 4 |
| 8778.75000 | 17.2049999 | 4.00000019E-03 | 4 |
| 8788.75000 | 17.1889992 | 4.99999989E-03 | 4 |
| 8797.75000 | 17.2469997 | 4.99999989E-03 | 4 |
| 8802.50000 | 17.1669998 | 1.09999999E-02 | 4 |
| 8805.50000 | 17.1959991 | 3.00000003E-03 | 4 |
| 8823.55176 | 17.1121445 | 1.20000001E-02 | 2 |
| 8834.75000 | 17.1529999 | 9.99999978E-03 | 4 |
| 8838.75000 | 17.1910000 | 4.00000019E-03 | 4 |
| 8878.75000 | 17.1229992 | 3.00000003E-03 | 4 |
| 8883.50000 | 17.0970001 | 2.00000009E-03 | 4 |
| 8892.50000 | 17.0909996 | 8.99999961E-03 | 4 |
| 8906.50000 | 17.1269989 | 6.00000005E-03 | 4 |
| 8909.50000 | 17.0479984 | 8.99999961E-03 | 4 |
| 8913.50293 | 17.0949993 | 4.99999989E-03 | 3 |
| 8920.50293 | 17.1130009 | 4.00000019E-03 | 3 |
| 8928.26728 | 17.1011489 | 0.012 | 2 |
| 9081.58692 | 17.1188643 | 0.012 | 2 |
Note. The epoch is given as the Julian Dates (−2,450,000). The last column denotes four different instruments used to obtain the photometric data: 1. CATALINA, 2. SALTICAM, 3. OGLE, 4. BMT. The BMT photometric points were shifted by 0.2 mag toward lower magnitudes to optimize the match with the OGLE photometry.
Appendix B: Redshift and Fe II Template
Precise determination of the redshift for quasar HE 0435-4312 is challenging, although its spectrum is not affected by absorption. The original redshift for the quasar, z =1.232 ± 0.001, was reported by Wisotzki et al. (2000) from the position of the Mg ii line. Marziani et al. (2009) measured the redshift on the basis of the Hβ line from VLT/ISAAC IR spectra, deriving z = 1.2321 ± 0.0014. A narrow [O iii] line was also visible in the spectrum, but it was strongly affected by atmospheric absorption, so it could not serve as a reliable redshift mark. Sredzińska et al. (2017) determined the redshift as z = 1.2231 using the data from SALT collected during the first three years of the SALT monitoring of this source. In this paper, two kinematic components were used to fit the Mg ii line: one component at the systemic redshift, together with the Fe II template, and the shift of the second was a model parameter. What is more, Sredzińska et al. (2017) showed that the Mg ii line position systematically changes with time. Thus the redshift was mostly determined by the location of the strong Fe II emission at 2750 Å.
In the currently available set of observations, one set, obtained on 2019 December 5 (observation 23), was obtained with a slightly shifted setup, so it covered the spectral range almost up to 3000 Å in the rest frame (in all other observations, this region overlaps with a CCD gap). Observed quasar spectra usually have a clear gap just above 2900 Å, which could serve as additional help in constraining the redshift, as well as the optimum Fe II template.
The basic template d11-m20-20.5-735 (marked later as d11) of Bruhweiler & Verner (2008) (with parameters: plasma density 1011 cm−3, turbulence velocity 20 km s−1, and log of ionization parameter in cm−2 s−1 of 20.5) favored by Sredzińska et al. (2017) does not fit well the dip in the region of 2900 Å (see Figure 10). We also checked other theoretical templates provided by Bruhweiler & Verner (2008), but all of them predicted considerable emissivity in that spectral region. Since the CLOUDY code has been modified over the years, we calculated new Fe II templates using the newest version of the code (Ferland et al. 2017), but with the same input as in the template d11, including the spectral shape of the incident continuum. New results did not solve the problem, and actually gave a much worse fit (see Table 4), if the two-Lorentzian model was assumed for the Mg ii line, as in Sredzińska et al. (2017). If, instead, we used two Gaussians for the line fitting, the resulting χ2 became much better (see Table 4) but still higher than with the older template, and the emission above 2900 Å was still overproduced. We thus experimented with simple removal of a few transitions from the original d11 template. We removed transitions at λλ2896.32, 2901.96, 2907.61, and 2913.28, creating the d11mod template. This clearly allowed a satisfactory representation of the data to be achieved, and favored the same redshift as in Sredzińska et al. (2017).
Figure 10. Selected models of observation 23 from Table 4.
Download figure:
Standard image High-resolution imageTable 4. Summary of the Redshift and Fe II Templates Used to Fit Observation 23
| Mg ii Model | Fe II Template | Redshift | FWHM (Fe II) | χ2 | Panel in Figure 10 |
|---|---|---|---|---|---|
| LL | d11 | 1.2231 | 3100 | 1377.59436 | a |
| LL | d11BV08-C17 | 1.2231 | 3100 | 1818.21631 | b |
| GG | d11BV08-C17 | 1.2231 | 3100 | 1505.38 | c |
| GG | d12-MaFer-C17 | 1.2321 | 2800 | 1517.13757 | |
| LL | d11mod | 1.2231 | 3100 | 1296.09912 | d |
| LL | KDP15 | 1.2321 | 3600 | 1408.91748 | |
| LL | KDP15 | 1.2321 | 4000 | 1400.57812 | e |
| LL | KDP15 | 1.2330 | 4000 | 1370.64978 | f |
Download table as: ASCIITypeset image
Next, we tried the KDP15 Fe II templates (Kovačević-Dojčinović & Popović 2015; Popović et al. 2019), which have fewer transitions but an additional flexibility of arbitrarily changing the normalization of each of the six transitions. This template provided a good fit for another of the quasars monitored with SALT (Zajaček et al. 2020). The clear disadvantage is that fitting these templates is much more time-consuming, since then the spectral model has 13 free parameters instead of eight, when the Fe II template has just one normalization as a free parameter. Nevertheless, we fitted all parameters at the same time, as in our standard approach.
The KDP15 template gave a rather poor fit for the low values of redshift favored by Sredzińska et al. (2017), but the model gave much lower χ2 values for the redshift range suggested by Marziani et al. (2009) (see Table 4). The best fit for this template was achieved for the redshift z = 1.2330, even slightly higher than in Marziani et al. (2009). However, formal χ2 is still higher than for the d11mod template. Since the two redshifts and the Fe II templates used for modeling in these two cases are so different, we checked how this difference in the spectrum decomposition actually affects the Mg ii line. For that purpose, we subtracted the fitted Fe II template and continuum from the original spectrum. The result is displayed in Figure 11 (left panel) in the observer's frame. As we see, the difference in the actual Mg ii shape is not large, despite large differences in the Fe II templates. The FWHM of the line is only slightly broader for KDP15, 3632 km s−1 versus 3507 km s−1, as determined from the total line shape. Line dispersion σ measured as the second moment differs more (3060 km s−1 versus 3423 km s−1) but in both cases the ratio FWHM/σ is much smaller than expected for a Gaussian profile.
Figure 11. Comparison between the fits of the observed Mg ii and Fe II complexes performed using d11mod and KDP15 models. Left panel: Mg ii line shape in the observer's frame after subtraction of Fe II and a power law with models d11mod from panel (d) of Figure 10 (red line) and KDP15 from panel (f) (blue line). The normalization is the same as in Figure 10, so the slight difference in the line normalization between the two models is visible. Right panel: the ratio of χ2 values between the fits performed using the d11mod model (z = 1.2231) and the KDP15 model (z = 1.2330) for available observational epochs. For 17 epochs out of 25,  .
.
Download figure:
Standard image High-resolution imageSince fitting the full six-transition KDP15 template is time-consuming, and we do not expect considerable changes in Fe II shape in the SALT data, we constructed a new single-parameter template based on KDP15, taking the relative values of the six components from the best fit of observation 23 in the extended wavelength range, and using the (best) Fe II broadening of 4000 km s−1. With this new template KDP15, we refitted all SALT observations in the range 2700–2900 Å . For 17 observations  , and for eight KDP15 fitted the data better, but generally not significantly; see Figure 11 (right panel). We thus perform most of the time-delay computations with the d11mod template, and we illustrate the role of the template in the time-delay determination for the ICCF method—see Appendix C.1, where we show that the KDP15 template is associated with a comparable cross-correlation function and similar peak and centroid distributions as those for d11mod; see Figure 13.
, and for eight KDP15 fitted the data better, but generally not significantly; see Figure 11 (right panel). We thus perform most of the time-delay computations with the d11mod template, and we illustrate the role of the template in the time-delay determination for the ICCF method—see Appendix C.1, where we show that the KDP15 template is associated with a comparable cross-correlation function and similar peak and centroid distributions as those for d11mod; see Figure 13.
Appendix C: Overview of Methods for Time-delay Determination
C.1. Interpolated Cross-correlation Function
We first analyzed the continuum and Mg ii line-emission light curves using the interpolated cross-correlation function, which is a standard and well-tested method for assessing the time delay between the continuum and the line emission flux density (Peterson et al. 1998). Light curves are typically unevenly sampled, while the ICCF works with the continuum–line emission pairs with a certain time step of Δt = ti+1 − ti . The cross-correlation function for two light curves, xi and yi , with the same time step of Δt achieved by interpolation, evaluated for a time shift of τk = kΔt (k = 1, ..., N − 1), is defined as
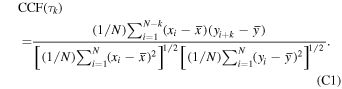
The same time step Δt can be achieved by interpolating the continuum light curve with respect to the line-emission light curve and vice versa (asymmetric ICCF). Typically, both interpolations are averaged to obtain the symmetric ICCF.
For the time-delay analysis, we use the Python implementation of ICCF in code PYCCF by Sun et al. (2018), which is based on the algorithm by Peterson et al. (1998). The code allows one to perform both asymmetric and symmetric interpolation. Based on the Monte Carlo techniques of random subset selection and flux randomization, one can obtain the centroid and the peak distributions and their corresponding uncertainties.
We studied the time delay between the continuum light curve consisting of 81 measurements, with eight Catalina-survey averaged detections, 16 SALTICAM measurement, 27 BMT data, and 30 OGLE data. Two SALTICAM measurements were excluded based on their poor quality. The emission-line light curve consists of 25 SALT measurements, where the 19th measurement has a poor quality due to weather conditions and is excluded from the further analysis. Hence, we have 79 continuum points with a mean cadence of 69.0 days and 24 Mg ii flux-density measurements with a mean cadence of 121.6 days. We set the interpolation interval to one day. For the redshift of z = 1.2231 and the d11mod template, we display the ICCF as a function of time delay in the observer's frame in Figure 12 (left panel) for both asymmetric and symmetric interpolation. In the middle and right panels, we show the centroid and the peak distributions for the symmetric interpolation based on 3000 Monte Carlo realizations of random subset selection and flux randomization. The centroid and the peak are generally not well defined. The peak value of the correlation function for the symmetric interpolation is 0.32 for a time delay of 635 days, which is less than for our previous quasars CTS C30.10 (peak CCF of ∼0.65, Czerny et al. 2019; Zajaček et al. 2019) and HE 0413-4031 (peak CCF of 0.8, Zajaček et al. 2020). In the next step, we focus on the surroundings of this peak and we analyze the CCF centroid and peak distributions in the interval between 500 and 1000 days. The results for all interpolations are summarized in Table 5. For the symmetric interpolation, we obtain a centroid time delay of  days and a peak time delay of
days and a peak time delay of  days.
days.
Figure 12. The interpolated cross-correlation function as a function of the time delay expressed in days in the observer's frame. The calculation is performed for the d11mod template and the redshift of z = 1.2231. Left panel: the ICCF as a function of the time delay expressed in days in the observer's frame for three types of interpolation: interpolated continuum light curve (green solid line), interpolated line light curve (blue solid line), and the symmetric interpolation (black solid line). Middle panel: the distribution of the cross-correlation centroids for the symmetric interpolation. Right panel: the distribution of the cross-correlation peaks for the symmetric interpolation.
Download figure:
Standard image High-resolution imageTable 5. Summary of the Time-delay Determination for the Quasar HE 0435-4312 Using the ICCF
| Interpolation Method | Time Delay (z = 1.2231) |
|---|---|
| Interpolated continuum—centroid [days] |

|
| Interpolated continuum—peak [days] |

|
| Interpolated line—centroid [days] |

|
| Interpolated line—peak [days] |

|
| Symmetric—centroid [days] |

|
| Symmetric—peak [days] |

|
Note. We list the centroids as well as the peaks for the interpolated continuum light curve, the interpolated line emission light curve, and the symmetric interpolation. Time delays are expressed in days in the observer's frame of reference.
Download table as: ASCIITypeset image
We also performed the time-delay analysis using the ICCF for the Mg ii light curve derived using the KDP15 template (case f in Table 4). For the symmetric ICCF, the CCF peak value is 692 days with CCF = 0.36, which is comparable to the analysis performed for the d11mod template. The CCF peak and centroid distributions also contain the same subpeaks, with the peak close to 700 days being the most prominent; see Figure 13.
Figure 13. The same ICCF analysis as in Figure 12 but for the KDP15 template (case f in Table 4) and the redshift of z = 1.2330.
Download figure:
Standard image High-resolution imageC.2. Discrete Correlation Function
For unevenly sampled and sparse light curves, the ICCF can distort the best time delay by adding additional data points to one or both light curves. In that case, the discrete correlation function (DCF) introduced by Edelson & Krolik (1988) is better suited to determine the best time lag.
In general, the DCF value is determined for any pair of light curves (xi , yj ) whose time difference Δtij falls into the time-delay bin of size δ τ, τ − δ τ/2 < Δtij < τ + δ τ/2, where τ is a given time delay. First, one calculates the unbinned DCF,
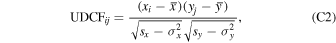
where  and
and  are light-curve means in a given time-delay bin, sx
and sy
are corresponding light curve variances, and σx
and σy
are the mean measurement errors of the light-curve points in the given time-delay interval.
are light-curve means in a given time-delay bin, sx
and sy
are corresponding light curve variances, and σx
and σy
are the mean measurement errors of the light-curve points in the given time-delay interval.
The DCF is then calculated as a mean over M light-curve points that are located in a given bin,
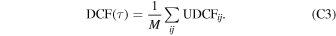
The uncertainty can be estimated using the relation
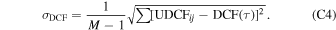
We made use of the Python script pyDCF (Robertson et al. 2015), where the general procedure described using Equations (C2), (C3), and (C4) is implemented. We searched for the DCF peak in the time interval from 100 to 1000 days, with a time step of 50 days. We obtained a better defined DCF peak using the Gaussian weighting scheme than using the slot weighting. In Figure 14 (left panel), we show the DCF versus time delay in the observer's frame. The time delay with the highest DCF value of 0.41 ± 0.16 is at 675 days. To determine the uncertainty of the peak, we ran 1000 bootstrap simulations, where at each step we constructed a pair of new light curves by randomly selecting a light-curve subset. The histogram of peak DCF time delays constructed from 1000 bootstrap realizations is shown in Figure 14 (right panel). The peak of the distribution is at  days in the observer's frame. The left and right uncertainties represent standard deviations, where we included the area within 30% of the main peak.
days in the observer's frame. The left and right uncertainties represent standard deviations, where we included the area within 30% of the main peak.
Figure 14. Discrete correlation function vs. a time delay in the observer's frame using the d11mod template. Left panel: a DCF vs. time delay in the observer's frame. A red vertical line denotes the peak DCF. Right panel: histogram of peak DCF time delays constructed from 1000 bootstrap realizations. The red and dashed green vertical lines denote the histogram peak and its left and right standard deviations within 30% of it, respectively.
Download figure:
Standard image High-resolution imageC.3. z-Transformed Discrete Correlation Function
In the following, we applied the z-transformed discrete correlation function (Alexander 1997), which improves the classical DCF by replacing equal time binning by equal population binning. This is achieved by applying Fisher's z-transform. With this property, the zDCF processes satisfactorily especially undersampled, sparse, and heterogeneous light curves, which to some extent is the case here, since the continuum light curve originates from three different instruments and the Mg ii light curve is relatively sparse with respect to the continuum (24 versus 79 points). In our analysis, we applied the zDCF method several times, changing the minimum number of light-curve pairs per population bin. Finally, we set the minimum number of light-curve pairs to eight and used 5000 Monte Carlo-generated pairs of light curves to determine the errors in each bin. In Figure 15, we show the zDCF values as a function of time delay in the observer's frame. There are some peaks with a large DCF value within the first 200 days in the rest frame, e.g., 190.3 days (DCF = 0.69). These are, however, too short to correspond to the realistic rest-frame time delay for our highly luminous quasar. The most prominent peak at larger time delays is at 646 days (DCF = 0.46).
Figure 15. The zDCF as a function of the time delay in the observer's frame. The uncertainties in each population bin were inferred from 5000 Monte Carlo-generated pairs of light curves (using the observed measurement errors). The red vertical line marks the most prominent, maximum-likelihood peak of  days, while the green vertical dashed lines mark the uncertainties.
days, while the green vertical dashed lines mark the uncertainties.
Download figure:
Standard image High-resolution imageNext we calculate the maximum likelihood (ML) using the zDCF values and we focus on the prominent peak in the interval between 500 and 800 days. From the ML analysis, we obtain the ML peak of  days in the observer's frame. This peak and the corresponding uncertainties are also highlighted in Figure 15 by vertical lines.
days in the observer's frame. This peak and the corresponding uncertainties are also highlighted in Figure 15 by vertical lines.
C.4. The JAVELIN Package
Another technique to evaluate the time-delay distribution is to model the continuum variability of AGNs as a stochastic process using the damped random walk process (Kelly et al. 2009; Kozłowski et al. 2010; MacLeod et al. 2010; Kozłowski 2016). Subsequently, the line emission is assumed to be time-delayed, smoothed, and a scaled version of the continuum emission. This method is implemented in the JAVELIN package (Just Another Vehicle for Estimating Lags in Nuclei; Zu et al. 2011, 2013, 2016) 15 . The package uses Markov Chain Monte Carlo (MCMC) methods to first determine the posterior probabilities for the continuum variability timescale and the amplitude. Based on that, the variability of the line emission is modeled to obtain the posterior probabilities for the time lag, smoothing width of the top-hat function, and the scaling ratio (the ratio between the line and the continuum amplitudes, Aline/Acont).
First, we searched for the time delay in the longer interval between 0 and 2000 days in the observer's frame. There are four distinct peaks (see Figure 16, left panel) at ∼100, ∼650, ∼1300, and ∼2000 days. The first peak is too short, while the last two appear too long for our data set. In the zDCF analysis in Section C.3, the time-delay peaks at 1000 days and more also have large uncertainties. Therefore, in the next search, we perform a time-delay search in the narrower interval between 0 and 1000 days to focus on the intermediate peak at ∼650 days. We obtain a prominent peak at ∼652 days; see Figure 16 (right panel).
Figure 16. The time-delay determination for HE 0435-4312 using the JAVELIN package. Left panel: the time-delay search in the interval between 0 and 2000 days in the observer's frame. There are four distinct peaks at ∼100, ∼650, ∼1300, and ∼2000 days. Right panel: the time-delay search in the narrower interval between 0 and 1000 days yields a clear peak at ∼652 days.
Download figure:
Standard image High-resolution imageTo determine the precise position of the time-delay peak, we performed 200 bootstrap simulations—i.e., generating 200 subsets of the original continuum and Mg ii light curves. Then we applied the JAVELIN to determine the peak time delay for each individual pair of light curves. From 200 best time delays, we first construct a density plot in the plane of the time delay and the scaling factor; see Figure 17 (left panel). We see that there is a peak in the distribution close to 600 days in the observer's frame. In Figure 17 (right panel), we show the histogram of the best time delays with the peak value of  days, where the uncertainties were determined within 30% of the peak value.
days, where the uncertainties were determined within 30% of the peak value.
Figure 17. Bootstrap analysis of the BLR time delay in HE 0435-4312 using the JAVELIN package. Left panel: the distribution of 200 best time delays in the plane of the time delay (in the observer's frame) and the scaling factor Aline/Acont. There is a prominent peak in the distribution close to 600 days. Right panel: the histogram of 200 best time delays. The peak value is at  days, which is marked by the vertical red and green dotted lines. The uncertainty is determined as the standard deviation within 30% of the main peak.
days, which is marked by the vertical red and green dotted lines. The uncertainty is determined as the standard deviation within 30% of the main peak.
Download figure:
Standard image High-resolution imageFor the JAVELIN time-delay determination, we typically notice several narrow comparable peaks in the histogram of time delays for a single MCMC run as can be seen in Figure 16. These secondary peaks typically arise due to a limited duration of observational runs and a sparse and/or nonuniform sampling of continuum and line-emission light curves. However, they might also reflect the complex BLR geometry seen in advanced data analysis or models (e.g., Grier et al. 2017; Hu et al. 2020; Horne et al. 2021; Naddaf et al. 2021). As mentioned in Grier et al. (2017), these alias peaks can be of a comparable significance to the true peak in the time-delay distribution, which is also the case here; see Figure 18 (right panel, black line), where time delays at ∼105, ∼1300, and ∼1980 days appear to have a larger significance than the fiducial peak of ∼650 days in the observer's frame.
Figure 18. Alias mitigation for the JAVELIN time-delay distribution. Left panel: prior probability distribution P(τ) = [N(τ)/N(0)]2 based on the number of overlapping data points for a given time delay. Right panel: posterior time-delay distributions before alias mitigation (black line) and after alias mitigation by using P(τ) as an effective weight for individual time-delay peaks.
Download figure:
Standard image High-resolution imageFollowing Grier et al. (2017), we weight the posterior probability distribution of time delays by the number of overlapping light-curve points, where the prior probability distribution is given by P(τ) = [N(τ)/N(0)]2, where N(τ) denotes the number of overlapping light-curve points for the time delay τ, and N(0) is the number of data points in the overlap region for zero time lag. Hence, the weight is P(τ) = 1 by definition for zero time lag and it will decrease for larger positive and negative time lags, being zero when there is no overlap. For our light curves, we construct the prior probability distribution P(τ), which is shown in Figure 18 (left panel).
Using P(τ), we weight the posterior time-delay distribution based on the number of overlapping light-curve points. This is demonstrated in Figure 18 (right panel, red line). The alias mitigation based on P(τ) helps to effectively suppress longer time-delays, which drop in significance below the fiducial time lag at ∼655 days. However, this technique is not efficient to suppress aliases at shorter time delays of ∼100 days, where the decrease is negligible due to the definition of P(τ). This peak at smaller time delays is effectively mitigated by the bootstrap or random subset selection technique. As we showed in Figure 17, this peak is not further represented in the posterior time-delay distribution, which leaves us with the fiducial peak close to ∼650 days. In addition, in Appendix D we show that the artifact peaks at ≲200 days arise in the probability density distributions (see Figures 22 and 23) constructed from mock light curves that are sampled with the same cadence as the original continuum and line-emission light curves.
C.5. Measures of Data Regularity/Randomness—von Neumann and Bartels Estimators
We also analyzed the time- delay between the continuum and Mg ii light curves using a novel technique of the measures of the data regularity or randomness (Chelouche et al. 2017), which were previously applied extensively in cryptography and data compression. The advantage of these regularity measures is that they do not require the interpolation as for the ICCF or χ2 technique and neither do they require binning in the correlation space like the DCF and zDCF methods. In addition, no AGN variability model is needed for the continuum light curve as for the JAVELIN.
One of the suitable estimators to analyze the time delay between two light curves is the optimized von Neumann scheme, which works with the combined light curve  , where F1 is the continuum light curve and
, where F1 is the continuum light curve and  is the time-shifted line-emission light curve. The optimized von Neumann estimator for a given time delay τ is defined as the mean of the successive differences of F(t, τ),
is the time-shifted line-emission light curve. The optimized von Neumann estimator for a given time delay τ is defined as the mean of the successive differences of F(t, τ),
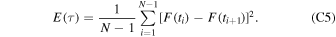
The aim of the von Neumann scheme is to find the minimum  , where
, where  is supposed to correspond to the actual time delay.
is supposed to correspond to the actual time delay.
In Figure 19 (left panel), we calculate E(τ) for HE 0435-4312 using the Python script based on Chelouche et al. (2017).
16
The minimum is reached for a time delay between 300 and 400 days in the observer's frame (333–334 days and 391–392 days), and then for 690 days, which is consistent with the results of previous methods. To determine the peak value and its uncertainty close to this minimum, we performed ∼10,000 bootstrap realizations, from which we constructed the histogram of the best von Neumann time delays; see Figure 19 (right panel). In this histogram, we detect two prominent peaks at ∼27 days and ∼1200 days and a smaller peak at ∼635 days. After focusing on the interval between 150 and 1100 days, the best peak is at  days in the observer's frame, where the uncertainties correspond to standard deviations within 30% of the best peak.
days in the observer's frame, where the uncertainties correspond to standard deviations within 30% of the best peak.
Figure 19. The results of the time-delay analysis using the von Neumann estimator. Left panel: the value of the von Neumann estimator as a function of the time delay in the observer's frame. The red vertical line denotes the minimum at 690 days. Right panel: the histogram of best von Neumann time delays constructed from 10,000 bootstrap simulations of random subset selections of both continuum and line-emission light curves. The red and green dotted vertical lines mark the peak value of  days and the corresponding uncertainties.
days and the corresponding uncertainties.
Download figure:
Standard image High-resolution imageFor comparison, we also applied the Bartels estimator to both light curves; it uses the ranked version of the combined light curve FR(t, τ). In Figure 20 (left panel), we show the Bartels estimator as a function of the time delay in the observer's frame. The minimum is clearer than for the von Neumann estimator and is located at 690 days. After running 10,000 bootstrap realizations, we detect three peaks as for the von Neumann estimator. Between 100 and 1100 days, there is a peak of  days (see Figure 20, right panel), where the uncertainties were calculated within 30% of this time-delay peak.
days (see Figure 20, right panel), where the uncertainties were calculated within 30% of this time-delay peak.
Figure 20. The results of the time-delay analysis using the Bartels estimator. Left panel: the value of the Bartels estimator as a function of the time delay in the observer's frame. The minimum estimator value is reached for a time delay of 690 days. Right panel: the histogram of best Bartels time delays constructed from 10,000 bootstrap simulations of random subset selections of both continuum and line-emission light curves. The red and green dotted vertical lines mark the peak value of  days and the corresponding uncertainties.
days and the corresponding uncertainties.
Download figure:
Standard image High-resolution imageC.6. The χ2 Method
Inspired by the time-delay analysis in quasar lensing studies, we applied the χ2 method to our set of light curves. The χ2 method performed well and consistently in comparison with other time-delay analysis techniques for the previous two SALT quasars—CTS C30.10 (Czerny et al. 2019) and HE 0413-4031 (Zajaček et al. 2020). It also performs better than the classical ICCF for the case when the AGN variability can be interpreted as a red-noise process (Czerny et al. 2013). We subtracted the mean from both the continuum and the line-emission light curves, and subsequently they were normalized by their corresponding variances. The similarity between the continuum and the time-shifted line-emission light curves is evaluated using χ2. We make use of symmetric interpolation.
In Figure 21 (left panel), we show χ2 as a function of the time delay in the observer's frame. There is a global minimum at 696 days. The exact position and the uncertainty of this peak are inferred from the histogram of the best time delays constructed from 10,000 bootstrap realizations. We obtain  days, where the uncertainties were determined as the left and the right standard deviations from the time delays that are positioned within 30% of the main peak; see Figure 21 (right panel).
days, where the uncertainties were determined as the left and the right standard deviations from the time delays that are positioned within 30% of the main peak; see Figure 21 (right panel).
Figure 21. Time-delay determination using χ2 method. Left panel: the χ2 value as a function of the time delay in the observer's frame. The global minimum is at ∼696 days, which is marked by a red vertical line. Right panel: the histogram of best time delays constructed from 10,000 bootstrap simulations around the global χ2 minimum of ∼700 days. The peak value is  days, which is shown using vertical red and green dotted lines.
days, which is shown using vertical red and green dotted lines.
Download figure:
Standard image High-resolution imageAppendix D: Alias Mitigation Using Generated Light Curves
In this appendix, we investigate the alias problem, i.e., the occurrence of secondary peaks in the time-delay distribution from a different perspective than presented in Appendix C.4, where we applied the downweighting technique on the posterior time-delay distribution based on the number of data points in the overlap region. Here we instead generate a large set of synthetic light curves similar in basic temporal properties to those of our studied quasar, while the line-emission light curve has a known prior time delay with respect to the continuum light curve. Then we apply several methods for time-delay determination to see how well we can recover the true time delay and what the distribution width is close to the assumed time delay.
To generate mock light curves, we use the method of Timmer & Koenig (1995) (hereafter TK) to produce synthetic light curves from the assumed shape and the normalization of the power density spectrum (PDS). The TK method can generate mock light curves based on any shape of PDS, unlike the damped random walk approach (Kelly et al. 2009; MacLeod et al. 2010; Zu et al. 2011, 2013, 2016), which generates light curves with the PDS slope close to −2. The assumed shape of the PDS is a broken power-law function with two break frequencies corresponding to ∼10,000 days at lower frequencies and to ∼700 days at higher frequencies. The slopes from lower to higher frequencies vary consequently from 0.0, through −1.2, up to −2.5. The line-emission light curve is first time-shifted by the assumed time delay, here fixed to 600 days in the observer's frame. Then the line emission is smeared by a timescale equal to 10% of the time delay, where we adopt the Gaussian shape of the BLR transfer function. Finally, dense continuum and line emission light curves are interpolated to the actual observational epochs of our observed light curves. We generate in total 1000 mock light curves with the actual observational cadence, which has the potential to reveal artifact peaks in the time-delay probability distributions due to the particular sampling pattern of our observations (see also Max-Moerbeck et al. 2014, for a similar analysis of cross-correlation artifacts). These corresponding continuum–line pairs are further analyzed by seven different time-delay methods. Subsequently, we construct histograms of best time delays, which are utilized as probability density distributions to determine the peak time delays and the corresponding 1σ uncertainties; see Figure 22 for the ICCF method and Figure 23 for the zDCF, JAVELIN, von Neumann, Bartels, DCF, and χ2 methods. In particular, we focus on how well we can determine the prior (true) time delay and what its uncertainty is. In Table 6, we list for individual methods the most prominent peaks and their uncertainties in the interval between 500 and 800 days in the observer's frame.
Figure 22. Best time-delay distribution constructed from the analysis of 1000 pairs of light curves generated using the Timmer–Koenig algorithm (Timmer & Koenig 1995) and subsequently analyzed by the interpolated cross-correlation function. The histogram of the best time delays has a bin size of 50 days. The dashed vertical line marks the time delay of 600 days in the observer's frame assumed for the time-shifted line-emission light curve.
Download figure:
Standard image High-resolution imageFigure 23. Best time-delay distributions constructed from 1000 pairs of light curves generated using the Timmer–Koenig algorithm (Timmer & Koenig 1995). Top left: the histogram of the best time delays constructed for the zDCF method. The bin size is 50 days. The dashed vertical line marks the time delay of 600 days in the observer's frame assumed for the time-shifted line-emission light curve. The other panels show analogous histograms of the best time delays constructed for the JAVELIN method (top right), the von-Neumann estimator (middle left), the Bartels estimator (middle right), the DCF method (bottom left), and the χ2 method (bottom right).
Download figure:
Standard image High-resolution imageTable 6. Peaks Close to τ = 600 days (in the Range between 500 and 800 days in the Observer's Frame) in the Time-delay Distributions (see Figure 23) for Individual Methods
| Method | Time-delay peak (days) |
|---|---|
| ICCF |

|
| zDCF |

|
| JAVELIN |

|
| Von Neumann |

|
| Bartels |

|
| DCF |

|
| χ2 |

|
Download table as: ASCIITypeset image
In general, the cadence of our observed light curves appears to produce two or three secondary peaks besides the prior peak close to 600 days, which are often more prominent than the assumed peak. Two peaks at ≲200 days and ∼900–1000 days are especially apparent. For the ICCF, DCF, and zDCF methods, the prior time-delay peak is not well defined, i.e., the distribution is highly smeared and broad in the interval between 500 and 800 days. For other methods, the peak close to 600 days is better defined, however, with a large standard deviation of the order of 100 days. The true peak at ∼600 days is best recovered using the JAVELIN method, which also suppresses effectively the secondary peaks detected in other methods. This result is consistent with the study of Yu et al. (2020b), who report that the JAVELIN outperforms the ICCF in terms of estimating time-delay error. Furthermore, Li et al. (2019) used mock light curves to compare the time-lag recovery and error estimation of the JAVELIN, ICCF, and zDCF and concluded that the JAVELIN produces higher quality time-delay estimations than both the ICCF and the zDCF. In Table 6, we list the inferred peaks in the range between 500 and 800 days, i.e., close to the true peak of 600 days in the observer's frame. We see that due to the sparse cadence of our observations, the detected peak can be shifted by as much as ∼100 days shortward or longward of the assumed peak.
The time-delay analysis of the generated light curves thus shows that secondary peaks can be created in the time-delay distribution due to the specific cadence and duration of the observed light curves. The secondary peaks longward of the true peak at 600 days can be mitigated using the downweighting technique as we showed in Appendix C.4 for the JAVELIN method; see also Grier et al. (2017). Here we show that the prominent peaks between 0 and ∼200 days, which are not mitigated by the downweighting due to a large number of overlapping light-curve pairs, can arise due to a lower cadence of our light curves, especially the line-emission light curve with only 24 points. Hence, they do not reflect the physical response of the BLR transfer function. In this sense, the reported mean peak time-delay of  days in the observer's frame (
days in the observer's frame ( days in the rest frame for z = 1.2231) for the quasar HE 0435-4312 can be considered as the best candidate for the true time delay, albeit with a large uncertainty up to ∼100 days. The other peaks appear to be aliases due to the specific cadence and the duration of our light curves.
days in the rest frame for z = 1.2231) for the quasar HE 0435-4312 can be considered as the best candidate for the true time delay, albeit with a large uncertainty up to ∼100 days. The other peaks appear to be aliases due to the specific cadence and the duration of our light curves.
Footnotes
- 9
More precisely, using the general dependence of f on the line FWHM in the form
 , with
, with  and β being the searched parameters, Mejía-Restrepo et al. (2018) obtained
and β being the searched parameters, Mejía-Restrepo et al. (2018) obtained  , β = −1.21 ± 0.24 for Mg ii and
, β = −1.21 ± 0.24 for Mg ii and  , β = −1.17 ± 0.11 for Hβ measurements.
, β = −1.17 ± 0.11 for Hβ measurements. - 10
NASA/IPAC Extragalactic Database: http://ned.ipac.caltech.edu/.
- 11
BMT is a part of the Universitaetssternwarte Bochum located near Cerro Armazones in Chile. For more information, see Ramolla et al. (2013).
- 12
- 13
- 14
- 15
- 16
For the script and the corresponding documentation, see www.pozonunez.de/astro_codes/python/vnrm.py.































