$\varLambda (1405)$ mediated triangle singularity in the $K^-d\rightarrow p\varSigma ^-$ reaction

Abstract

We study for the first time the $p\varSigma ^-\rightarrow K^-d$ and $K^-d\rightarrow p\varSigma ^-$ reactions close to threshold and show that they are driven by a triangle mechanism, with the $\varLambda (1405)$, a proton and a neutron as intermediate states, which develops a triangle singularity close to the ${\bar{K}}d$ threshold. We find that a mechanism involving virtual pion exchange and the $K^-p\rightarrow \pi ^+\varSigma ^-$ amplitude dominates over another one involving kaon exchange and the $K^-p\rightarrow K^-p$ amplitude. Moreover, of the two $\varLambda (1405)$ states, the one with higher mass around 1420 MeV, gives the largest contribution to the process. We show that the cross section, well within measurable range, is very sensitive to different models that, while reproducing ${\bar{K}}N$ observables above threshold, provide different extrapolations of the ${\bar{K}}N$ amplitudes below threshold. The observables of this reaction will provide new constraints on the theoretical models, leading to more reliable extrapolations of the ${\bar{K}}N$ amplitudes below threshold and to more accurate predictions of the $\varLambda (1405)$ state of lower mass.

1 Introduction

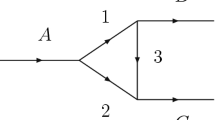
Introduced early in the 50’s [1, 2], the triangle singularities (TS) are getting a growing attention nowadays since they are helping to understand many phenomena observed in hadron physics. The singularity stems from a mechanism that can be depicted by a triangle Feynman diagram, see Fig. 1, where a particle A decays into 1 and 2, 1 decays into B and 3, and 2 and 3 merge to form particle C. If this mechanism can occur at the classical level, a singularity appears in the amplitude (Coleman–Norton theorem [3]), which requires that 1 and B move in the same direction in the A rest frame, and 3 moves in the direction of 2 and faster, such that it catches up with 2 and fuses with it to give C. The subject has been reformulated recently with a more intuitive and practical formalism in Ref. [4] and a thorough review has been done in Ref. [5].

Recent examples of TS are found in the study of the $\eta (1405)\rightarrow f_0(980) \pi ^0$ decay [6] performed in Refs. [7,8,9,10]. Another relevant case was the explanation of the “$a_1(1420)$” structure observed by the COMPASS collaboration [11], which is explained in terms of a TS in Refs. [12,13,14,15]. Some other recent examples can be seen in [16,17,18] and a rather complete list of reactions studied along TS is given in Ref. [5].

Another example of TS is given by the $\pi ^+d\rightarrow pp$ reaction [19, 20] which has been much studied in the past [21,22,23,24]. Recently, this latter reaction got again attention in [25] by looking at the time reversal reaction $pp\rightarrow \pi ^+d$, because it was shown to be driven by a triangle mechanism with $\varDelta NN'$ in the intermediate states and $NN'$ fusing to give the deuteron. This mechanism was found responsible for the relatively large cross section of the fusion reaction. The works of [21,22,23,24,25] share basically the same model. Particle A in Fig. 1 is the pp system, particle 1 is the $\varDelta (1232)$, B is a pion and 2, 3 are nucleons that merge to give C, which is the deuteron. The $pp \rightarrow N\varDelta$ transition is mediated by $\pi$ and $\rho$ exchange. The results are similar. Ref [25] uses the same model but a different formalism, in momentum space, which allows one to trace the triangle singularity of the process. At the same time, different spin transitions and angular distributions were evaluated and shown to be consistent with the results obtained in [24], where they were also studied. It was also shown in [25] that the dominant waves were in agreement with the experimental findings in [26,27,28].

In the present case we shall study the related $p\varSigma ^-\rightarrow K^-d$ ($K^-d\rightarrow p\varSigma ^-$) reactions, showing that the mechanism is similar to the one of the $pp\rightarrow \pi ^+d$ reaction, but now the high energy pole of the $\varLambda (1405)$ plays the role of the $\varDelta (1232)$ in the $pp\rightarrow \pi ^+d$ reaction. The TS places this $\varLambda (1405)$ and the nucleons of the triangle diagram on shell and this leads to the interesting result that one can see the effects of the $\varLambda (1405)$, which lies below the ${\bar{K}}N$ threshold, in a reaction with physical kaons, in other words, we observe effects of the $K^-p$ amplitudes below threshold in a reaction with kaons above threshold. This is most welcome, since different theoretical models for the ${\bar{K}}N$ interaction reproducing well the data above the ${\bar{K}}N$ threshold lead to quite different results for the amplitudes below threshold.

Fig. 1

Feynman diagram from where a triangle singularity can emerge. Particle A decays into 1 and 2, 1 decays into B and 3, and 2 and 3 merge to form particle C

Fig. 2

Feynman diagrams for the $p\varSigma ^-\rightarrow K^-d$ reaction. The momenta of the lines are shown in brackets

The ${\bar{K}}N$ interaction has been the subject of intense theoretical scrutiny [29,30,31,32] which has been reinforced with the advent of the chiral unitary approach [33,34,35,36,37,38]. One surprise from the use of this approach is the existence of two $\varLambda (1405)$ states [36, 39] which have found their way into the PDG [40] only recently. A large amount of papers have come to corroborate this finding [41,42,43,44,45,46,47,48,49,50,51,52]. Reviews on this issue can be seen in [53,54,55,56]. Yet, in spite of reproducing the ${\bar{K}}N$ data above threshold and some threshold observables, the different models produce ${\bar{K}}N$ amplitudes below threshold which differ much from each other (see Fig. 1 of [57]). We will show that because the reaction relies upon ${\bar{K}}N$ amplitudes below threshold, the results that we obtain with several models for the ${\bar{K}}N$ interaction lead to results for the $K^-d\rightarrow p\varSigma ^-$ reaction that differ appreciably among themselves. In other words, the measurement of this cross section would provide an extra valuable observable to put more constraints on the theoretical models and make them more predictive below the ${\bar{K}}N$ threshold. This information would go in the same line of the work presently done at DAFNE in the programs as AMADEUS [58] and SIDDHARTA [59].

2 Formalism

We shall study the $p\varSigma ^-\rightarrow K^-d$ reaction to be able to exploit the analogies with the $pp\rightarrow \pi ^+d$ reaction. The process proceeds via the diagrams of Fig. 2.

The process of $p\varSigma ^-\rightarrow K^-d$, involving the fusion of the two nucleons in the final state, can be visualized from the time reversed point of view as a mechanism of $K^-$ absorption on two nucleons, with the mechanisms of $K^-$ absorption described in [60,61,62].

The diagrams of Fig. 2 develop a triangle singularity. This occurs when the $\varLambda (1405)$, the p and n intermediate states are placed on shell in the loop (the $K^+$ and $\pi ^-$ are off shell and do not matter for the discussion of the TS) and the $\varLambda (1405)$ and $K^-$ are in the same direction. If the proton, which goes in the same direction of the neutron in this case, goes faster than the neutron, it can catch up with the neutron and fuse into the deuteron, producing the TS according to the Coleman–Norton theorem [3]. All these conditions are summarized in Eq. (18) of Ref. [4] in the limit of zero width of the $\varLambda (1405)$, which states

$$\begin{aligned} q_\textrm{on}=q_{a^-} \end{aligned}$$

(1)

where $q_{\textrm{on}}$ is the momentum of the neutron in the $p\varSigma ^-$ rest frame and $q_{a^-}$ is one of the solutions of the momentum of the neutron in the decay of the d into pn for the moving d in the $p\varSigma ^-$ rest frame. Easy analytical formulae for $q_{\textrm{on}}$, $q_{a^-}$ are given in Ref. [4]. This condition requires that the p, n and $\varLambda ^*$ in the loop are on shell. Technically, the deuteron bound does not decay to pn, and to test Eq. (1) one can take a deuteron slightly unbound. The singularity becomes a broad peak upon the consideration of the $\varLambda (1405)$ width and, by continuity, it shows up even if the deuteron is bound by 2.2 MeV. The test of Ref. [4] is done here taking the deuteron mass of 1878 MeV, which is 0.2 MeV above np threshold, and the $\varLambda (1405)$ mass equal to 1434 MeV, just 2 MeV above the $K^-p$ threshold. This mass is 8 MeV above the mass of the upper $\varLambda (1405)$ state found in Ref. [39] at 1426 MeV, which has a width of 32 MeV. This guarantees a large overlap with the TS condition. Under these assumptions, needed to pass the test of Ref. [4], the TS is obtained at 2373.65 MeV where $q_\textrm{on}=q_{a^-}=10$ MeV/c. Technically one would perform the $K^-d\rightarrow p\varSigma ^-$ measurement, which can be done for low $K^-$ energies in DAFNE [63] and in other facilities, as JPARC [64, 65] or the planned kaon facility at Jefferson Lab [66, 67].

To evaluate the amplitudes for the diagrams of Fig. 2 one needs the coupling of the two $\varLambda (1405)$ to $K^-p$ and to $\pi ^+\varSigma ^-$ and the couplings of $\pi ^-p\rightarrow n$ and $K^+\varSigma ^- \rightarrow n$. The $\pi ^-pn$ coupling is given for an incoming $\pi ^-$ of momentum $\textbf{q}$ by

$$\begin{aligned} -it=\frac{f_{\pi NN}}{m_\pi }\mathbf {\sigma }\cdot \textbf{q}\sqrt{2}\ , \end{aligned}$$

(2)

with $f_{\pi NN}=1.002$. Alternatively, this coupling and in general the pseudoscalar-meson baryon vertex (PBB), can be obtained from chiral Lagrangians [68, 69] and the general result is given by [70],

$$\begin{aligned} -it_{{\bar{K}}NY}=\left[ \alpha \frac{D+F}{2f}+\beta \frac{D-F}{2f}\right] \mathbf {\sigma }\cdot \textbf{q} \end{aligned}$$

(3)

for an incoming ${\bar{K}}$, with $f=93$ MeV, $D=0.795$, $F=0.465$ [71]. In particular,

$$\begin{aligned} -it_{K^+\varSigma ^-\rightarrow n}=\sqrt{2}\frac{D-F}{2f}\mathbf {\sigma }\cdot \textbf{q} \end{aligned}$$

(4)

We note that in this formalism, $\frac{f_{\pi NN}}{m_\pi }=\frac{D+F}{2f}$. The isospin $I=0$ function for the deuteron can be written as

$$\begin{aligned} \vert d\rangle =\frac{1}{\sqrt{2}}(\vert pn\rangle -\vert np\rangle ) . \end{aligned}$$

(5)

The coupling of the deuteron to NN is given by $g_d$. In particular for the pn component

$$\begin{aligned} -it_{dpn}=-ig_d\frac{1}{\sqrt{2}}\theta (q_\textrm{max}-\vert \textbf{q}\vert _{\mathrm {c.m.}}) \end{aligned}$$

(6)

where $\textbf{q}_{\mathrm {c.m}}$ is the p momentum in the d rest frame. From the study in Appendix A of [25], we find

$$\begin{aligned}{} & {} g_d=(2\pi )^{(3/2)}2.67\times 10^{-3} \textrm{MeV}^{-1/2} ,\nonumber \\{} & {} q_\textrm{max}=240\,\textrm{MeV} . \end{aligned}$$

(7)

With these ingredients we can evaluate the amplitudes corresponding to the two diagrams of Fig. 2 and find

$$\begin{aligned}&-it^{(a)}= (-i)g_{\varLambda ^*,K^-p}(-i)g_{\varLambda ^*,K^-p}(-i) g_d\frac{D-F}{2f}\nonumber \\&\quad \int \frac{d^4q}{(2\pi )^4}\mathbf {\sigma }_2\cdot \textbf{q}\frac{i}{q^2-m^2_K+i\epsilon }\frac{M_{\varLambda ^*}}{E_{\varLambda ^*}}\frac{i}{P^0-q^0-E_{\varLambda ^*}(\textbf{P}-\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\nonumber \\&\times \frac{M_{N}}{E_{N}}\frac{i}{P^0-q^0-k^0-E_{N}(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\&\quad \frac{M_N}{E'_N}\frac{i}{P'^0+q^0-E'_N(-\textbf{P}+\textbf{q})+i\epsilon }\theta (q_\textrm{max}-\vert \textbf{P}-\textbf{q}-\frac{\textbf{k}}{2}\vert ),\nonumber \\&-it^{(b)}=-g_{\varLambda ^*,K^-p}g_{\varLambda ^*,\pi ^+\varSigma ^-}g_d\frac{f_{\pi NN}}{m_\pi }i\nonumber \\&\quad \int \frac{d^4q}{(2\pi )^4}\frac{1}{q^2-m^2_\pi +i\epsilon } \frac{M_{\varLambda ^*}}{E_{\varLambda ^*}}\frac{1}{P'^0-q^0-E_{\varLambda ^*}(-\textbf{P}-\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\nonumber \\&\times \mathbf {\sigma }_1\cdot \textbf{q}\,\frac{M_N}{E_N}\frac{1}{P'^0-q^0-k^0-E_N(-\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\&\quad \frac{M_N}{E'_N}\frac{1}{P^0+q^0-E'_N(\textbf{P}+\textbf{q})+i\epsilon }\theta (q_{\textrm{max}}-|-\textbf{P}-\textbf{q}-\frac{\textbf{k}}{2}|), \end{aligned}$$

(8)

where $E(\textbf{P})=\sqrt{\textbf{P}^2+m^2}$. We write the pseudoscalar propagator as

$$\begin{aligned} \frac{1}{\textbf{q}\,^2-m^2+i\epsilon } = \frac{1}{2\omega (\textbf{q})}\left( \frac{1}{q^0-\omega (\textbf{q})+i\epsilon } -\frac{1}{q^0+\omega (\textbf{q})-i\epsilon }\right) ,\nonumber \\ \end{aligned}$$

(9)

with $\omega (\textbf{q})=\sqrt{m^2+\textbf{q}\,^2}$, and then perform the $q^0$ integration analytically. However, it is practical to reduce the number of denominators containing $q^0$ and for this purpose it is useful to write

$$\begin{aligned}{} & {} \frac{1}{P^0-q^0-k^0-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\{} & {} \frac{1}{P^{'0}+q^0-E_N'(-\textbf{P}+\textbf{q})+i\epsilon }\nonumber \\{} & {} =\frac{1}{\sqrt{s}-k^0-E_N(-\textbf{P}+\textbf{q})-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\{} & {} \quad \times \left( \frac{1}{P^0+q^0-k^0-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\right. \nonumber \\{} & {} \quad \left. +\frac{1}{P^{'0}+q^0-E_N'(-\textbf{P}+\textbf{q})+i\epsilon }\right) . \end{aligned}$$

(10)

Then we easily find using Cauchy’s theorem that

$$\begin{aligned}&-it^{(a)}_{ij}=g_{\varLambda ^*,K^-p}\,g_{\varLambda ^*,K^-p}\,g_d\frac{D-F}{2f}\nonumber \\&\quad \int \frac{d^3q}{(2\pi )^3}V_{ij}(q)F(P^0,P^{'0},\textbf{q},\omega _K(\textbf{q}),\textbf{P},\textbf{k}) {\mathcal {F}}^2 (\varLambda , m_K)\nonumber \\&-it^{(b)}_{ij}=-g_{\varLambda ^*,K^-p}\,g_{\varLambda ^*,\pi ^+\varSigma ^-}g_d\frac{f_{\pi NN}}{m_\pi }\nonumber \\&\quad \int \frac{d^3q}{(2\pi )^3}W_{ij}(q)F(P^{'0},P^0,\textbf{q},\omega _\pi (\textbf{q}),-\textbf{P},\textbf{k}){\mathcal {F}}^2 (\varLambda , m_\pi ), \end{aligned}$$

(11)

where ${\mathcal {F}} (\varLambda , m_i)$ and $F(P^0,P'^0,\textbf{q},\omega ,\textbf{P},\textbf{k})$ are given by

$$\begin{aligned} {\mathcal {F}} (\varLambda , m_i) = \frac{\varLambda ^2-m_i^2}{\varLambda ^2+\textbf{q}^2} , \end{aligned}$$

(12)

and

$$\begin{aligned}&F(P^0,P'^0,\textbf{q},\omega ,\textbf{P},\textbf{k})=\frac{1}{2\omega (\textbf{q})}\frac{M_N}{E_N(\textbf{P}-\textbf{q}-\textbf{k})}\nonumber \\&\qquad \frac{M_N}{E_N(-\textbf{P}+\textbf{q})}\frac{M_{\varLambda ^*}}{E_{\varLambda ^*}(\textbf{P}-\textbf{q})}\nonumber \\&\times \frac{\theta (q_\textrm{max}-|\textbf{P}-\textbf{q}-\frac{\textbf{k}}{2}|)}{\sqrt{s}-k^0-E_N(-\textbf{P}+\textbf{q})-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\&\times \left\{ \frac{1}{P^0-\omega (\textbf{q})-E_{\varLambda ^*}(\textbf{P}-\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\right. \nonumber \\&\qquad \left. \frac{1}{P^0-\omega (\textbf{q})-k^0-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\right. \nonumber \\&+\frac{1}{P^0-E_{\varLambda ^*}(\textbf{P}-\textbf{q})-\omega (\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\nonumber \\&\qquad \frac{1}{\sqrt{s}-E_{\varLambda ^*}(\textbf{P}-\textbf{q})-E_N(-\textbf{P}+\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\nonumber \\&+\frac{1}{P'^0-E_N(-\textbf{P}+\textbf{q})-\omega (\textbf{q})+i\epsilon }\left. \right. \nonumber \\&\qquad \left. \frac{1}{\sqrt{s}-E_{\varLambda ^*}(\textbf{P}-\textbf{q})-E_N(-\textbf{P}+\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\right\} . \end{aligned}$$

(13)

We have also introduced a form factor to account for the pseudoscalar exchange with $\varLambda =1125$ MeV as also used in [25]. The functions $V_{ij}(q)$, $W_{ij}(q)$ are the matrix elements of $\mathbf {\sigma }_2\cdot \textbf{q}$ and $\mathbf {\sigma }_1\cdot \textbf{q}$ respectively for the spin transitions $i\rightarrow j$ with $i=\uparrow \uparrow , \uparrow \downarrow ,\downarrow \uparrow ,\downarrow \downarrow$ for the $p\varSigma ^-$ spins and $j=\uparrow \uparrow ,\frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow )$, $\downarrow \downarrow$ for the deuteron polarizations. The explicit expressions of $V_{ij}$, $W_{ij}$ are shown in Appendix A.

The procedure we follow to do the fourfold integration is rewarding. We first perform the $q^0$ integration analytically where the poles of the propagators of the four internal particles of the loop are considered, including the pion poles of Eq. (9). After this is done, we are left with the threefold integration of Eq. (11) which we perform numerically. The factors F of Eq. (11), (13) contain now the full analytical structure of the amplitude and we can see explicitly which are the remaining poles by setting to zero the denominators appearing in Eq. (13). Taking as example the amplitude $t^{(b)}$ which contains the pion propagator and involves $F(P^{'0},P^0,\textbf{q},\omega _\pi (\textbf{q}),-\textbf{P},\textbf{k})$, we have the following cuts:

• a) $\sqrt{s}-k^0=E_N(\textbf{P}+\textbf{q})+E_N(\textbf{P}+\textbf{q}+\textbf{k})$. This pole places the two nucleons of the loop on shell.

• b) $P'^0=\omega _{\pi }(\textbf{q})+E_{\varLambda ^*}(\textbf{P}+\textbf{q})$. This pole corresponds to the impossible case of a $\varSigma ^-$ producing a $\pi$ and a $\varLambda (1405)$. Hence, the denominator of this propagator will never be zero.

• c) $P'^0=\omega _{\pi }(\textbf{q})+k^0+E_N(\textbf{P}+\textbf{q}+\textbf{k})$. Once again this relationship will never be fulfilled and the inverse of the propagator will never be zero.

• d) $\sqrt{s}=E_{\varLambda ^*}(\textbf{P}+\textbf{q})+E_N(\textbf{P}+\textbf{q})$. This places the $\varLambda ^*$ and the upper nucleon of diagram (b) in Fig. 2 on shell and can occur.

• e) $P^0=E_N(\textbf{P}+\textbf{q})+\omega _{\pi }(\textbf{q})$. This is again impossible because a nucleon cannot go to a nucleon and a pion.

As we can see, only the propagators corresponding to cases a) and d) can have zero denominators and give rise to cuts in the amplitudes. However, in an ordinary case the $d^3q$ integral gives the principal values and the imaginary parts in the amplitude. The infinites of the denominator to the left and right of the singular point have opposite sign and cancel in the principal value of the $dq'$ integral with $\mathbf {q'}=\textbf{P}+\textbf{q}$. Yet, because of the $E_i(\textbf{P}+\textbf{q}+\textbf{k})$ terms in the denominators, one has two integrations, one in $dq'$ and the other one in $dcos\theta$, with $\theta$ the angle between $\textbf{P}+\textbf{q}$ and $\textbf{k}$. If we have a singularity at $cos\theta =\pm 1$ then in the $dcos\theta$ integration we cannot benefit from the cancellations of the two infinite branches, because we cannot integrate beyond $cos\theta =1$ or below $cos\theta =-1$ and then an infinite arises. Actually the cut a) has two algebraic solutions for $cos\theta =-1$, keeping the $i\epsilon$ of the denominators, $q'_{a_-}-i\epsilon$, $q'_{a_+}+i\epsilon$, easily obtained as

$$\begin{aligned} q'_{a_-}=\gamma (vE^*_2-p^*_2) ; \, \, \, q'_{a_+}=\gamma (vE^*_2+p^*_2) \end{aligned}$$

where v is the velocity of the deuteron in the $p\varSigma ^-$ rest frame, and $p^*_2$, $E^*_2$ the momentum and energy of the upper nucleon of the diagram in the d rest frame, with $\gamma =(1-v^2)^{-\frac{1}{2}}$. The cut d) has as solutions $q'=q'_{on}+i\epsilon$ and $q'=-q'_{on}-i\epsilon$, but the second is irrelevant since we integrate over $|\mathbf {q'}|$ positive. On the other hand, when $cos\theta =1$ for the cut a), the algebraic solutions are $q'_{b_-}-i\epsilon$, $q'_{b_+}+i\epsilon$ with

$$\begin{aligned} q'_{b_-}=-\gamma (vE^*_2+p^*_2) ; \, \, \, q'_{b_+}=\gamma (-vE^*_2+p^*_2) \end{aligned}$$

and, again the $q'_{b_-}$ solution is irrelevant since we integrate over positive $|\mathbf {q'}|$. We can see that for $cos\theta =1$ the singular points are $q'_{on}+i\epsilon$ and $q'_{b_+}+i\epsilon$, both of them in the upper side of the complex plane and can be sorted out in the $\int ^\infty _0dq'$ integral by deforming the integration contour. However for $cos\theta =-1$ if we take $q'_{a_-}-i\epsilon$ and $q'_{on}+i\epsilon$ with $q'_{on}=q'_{a_-}$ we are forced to pass between the two poles in the $\int ^\infty _0dq'$ integration no matter how the integration contour is deformed and this time one has an infinite in the amplitude in the case that we neglect the with of the $\varLambda ^*$ (illustrative figures of the situation in the general case can be seen in Fig. 3 of Ref. [4]). This is the triangle singularity situation [1, 2] as explained in detail in Ref. [4]. In the former discussion we have also seen that the denominators involving the pion never become zero, which is the technical way of expressing that the pion is never on shell in that diagram.

The cross section for the $K^-d\rightarrow p\varSigma ^-$, which is what would be measured, is given by

$$\begin{aligned} \frac{d\sigma }{d\textrm{cos}\,\theta _p}=\frac{1}{4\pi }\frac{1}{s}M_pM_{\varSigma ^-}M_d\frac{p}{k}{\bar{\sum }}\sum \vert t\vert ^2 \end{aligned}$$

(14)

where

$$\begin{aligned} t=t^{(a)}+t^{(b)} \end{aligned}$$

(15)

and

$$\begin{aligned} {\bar{\sum }}\sum \vert t\vert ^2=\frac{1}{3}\sum _{i,j}\vert t_{ij}^{(a)}+t_{ij}^{(b)}\vert ^2 , \end{aligned}$$

(16)

with i, j referring to the initial and final spin states.

For the evaluation of the $p\varSigma ^-\rightarrow K^-d$ amplitudes we take $\textbf{P}=P(0,0,1)$, $\textbf{k}=k(\textrm{sin}\,\theta _K,0,\textrm{cos}\,\theta _K)$ and $\textbf{q}\equiv q(\textrm{sin}\,\theta \textrm{cos}\,\phi , \textrm{sin}\,\theta \,\textrm{sin}\,\phi ,\textrm{cos}\,\theta )$. Note that $\textrm{cos}\,\theta _p$ in $K^-d\rightarrow p\varSigma ^-$ is the same as $\textrm{cos}\,\theta _K$ in $p\varSigma ^-\rightarrow K^-d$.

The factor p/k of phase space in Eq. (14) makes the cross section blow up as $k\rightarrow 0$. For this reason we find appropriate to plot $\frac{k}{p}\left( \frac{d\sigma }{d\textrm{cos}\theta _p}\right)$, or $\frac{k}{p}\sigma$, after integration over angles.

Since we have two $\varLambda (1405)$ poles, we must sum over them in the $t^{(a)}_{ij}$ or $t^{(b)}_{ij}$ amplitudes. We obtain these amplitudes simply putting the couplings of the two resonances to the $K^-p$ or $\pi ^+\varSigma ^-$ in Eqs. (11) and the mass and width of the $\varLambda (1405)$ in Eq. (13). As a reference we will use the model of Ref. [35] with the properties of these resonances given in Table 1. In particular we have

$$\begin{aligned}{} & {} g_{\varLambda ^*,K^-p}=\frac{1}{\sqrt{2}}g_{\varLambda ^*,{\bar{K}}N}\nonumber \\{} & {} g_{\varLambda ^*,\pi ^+\varSigma ^-}=-\frac{1}{\sqrt{3}}g_{\varLambda ^*,\pi \varSigma } \end{aligned}$$

(17)

2.1 Relation to the explicit deuteron wave function

Following [72] and Appendix A of Ref. [25] (see also Eq. (34) of [25]), one can identify the deuteron wave function in momentum space in our formalism and replace it by the one of the Bonn model [72] (the results with the Paris wave function [73] are practically the same). The equivalence in the present case is¹

$$\begin{aligned}&g_d\frac{M_N}{E(\textbf{P}-\textbf{q}-\textbf{k})}\frac{M_N}{E_N(-\textbf{P}+\textbf{q})}\nonumber \\&\qquad \frac{\theta (q_{\textrm{max}}-\vert \textbf{P}-\textbf{q}-\frac{\textbf{k}}{2}\vert )}{\sqrt{s}-k^0-E_N(-\textbf{P}+\textbf{q})-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\&\quad \longrightarrow -(2\pi )^{3/2}\psi (\textbf{P}-\textbf{q}-\frac{\textbf{k}}{2}) \end{aligned}$$

(18)

with $\psi (q)$ normalized as $\int d^3 q\vert \psi (\textbf{q})\vert ^2=1$.

2.2 Amplitudes using the explicit ${\bar{K}}N\rightarrow {\bar{K}}N$ and ${\bar{K}}N\rightarrow \pi \varSigma$

Since formally we have the equivalences of

$$\begin{aligned}&\sum _{i=1}^2\frac{M_{\varLambda ^*}^{(i)}}{E_{\varLambda ^*}^{(i)}(\textbf{P}-\textbf{q})}\frac{g^{(i)}_{\varLambda ^*,K^-p}g^{(i)}_ {\varLambda ^*,K^-p}}{\sqrt{s}-E_N(-\textbf{P}+\textbf{q})-E^{(i)}_{\varLambda ^*}(\textbf{P}-\textbf{q})+i\frac{\varGamma ^{(i)}_{\varLambda ^*}}{2}}\nonumber \\&\quad \equiv t_{K^-p,K^-p}(M_\textrm{inv}) \end{aligned}$$

(19)

and

$$\begin{aligned}&\sum _{i=1}^2\frac{M_{\varLambda ^*}^{(i)}}{E_{\varLambda ^*}^{(i)}(\textbf{P}-\textbf{q})}\frac{g^{(i)}_{\varLambda ^*,K^-p}g^{(i)}_{\varLambda ^*,\pi ^+\varSigma ^-}}{\sqrt{s}-E_N(\textbf{P}+\textbf{q})-E^{(i)}_{\varLambda ^*}(-\textbf{P}-\textbf{q})+i\frac{\varGamma ^{(i)}_{\varLambda ^*}}{2}}\nonumber \\&\quad \equiv t_{K^-p,\pi ^+\varSigma ^-}(M'_\textrm{inv}), \end{aligned}$$

(20)

with $M_{\textrm{inv}}^2=s+M^2_N-2\sqrt{s}E_N(-\textbf{P}+\textbf{q})$, and $M_{\textrm{inv}}'^2=s+M^2_N-2\sqrt{s}E_N(\textbf{P}+\textbf{q})$, respectively, we can write the amplitudes $t_{ij}^{(a)}$, $t_{ij}^{(b)}$ as

$$\begin{aligned}&-it^{(a)}_{ij}=g_d\frac{D-F}{2f}\nonumber \\&\quad \int \frac{d^3q}{(2\pi )^3}V_{ij}(q)F'(P^0,P'^{0},\textbf{q},\omega _K(\textbf{q}),\textbf{P},\textbf{k}) {\mathcal {F}}^2 (\varLambda , m_K),\nonumber \\&-it^{(b)}_{ij}=-g_d\frac{D+F}{2f}\nonumber \\&\quad \int \frac{d^3q}{(2\pi )^3}W_{ij}(q)G'(P^{0},P'^0,\textbf{q},\omega _\pi (\textbf{q}),\textbf{P},\textbf{k}){\mathcal {F}}^2 (\varLambda , m_\pi ), \end{aligned}$$

(21)

where $F'$ and $G'$ are given in Appendix B.

Table 1 Pole positions and couplings from Ref. [39]

3 Results

In the first place, we study the contribution of the different spin transitions. We use the model of Ref. [35] (called Oset-Ramos later) taking the input of Table 1. In Fig. 11, we shall present results for the cross sections using different models. The cross sections are taken from Eq. (14) subsequently integrated over the angle $\theta _p$. In Fig. 3 we plot $\frac{k}{p}\sigma$ for several spin transitions. One finds that the most important is $\uparrow \uparrow \rightarrow \uparrow \uparrow$, or $\downarrow \downarrow \rightarrow \downarrow \downarrow$ which has the same strength. The transitions involving some spin flip are very small as shown in Fig. 4. This spin dependence is different from the one obtained in the $pp \rightarrow \pi ^+d$ reaction [25] and the reason is that, unlike in [25], we have only a spin operator in one of the baryonic lines.

Next, we look at the angular dependence. Figure 5 displays the angular dependence of $d\sigma /d\textrm{cos}(\theta _p)$ for two given values of $\sqrt{s}$, namely about 10 MeV and 30 MeV above threshold.

Fig. 3

Contribution from several spin transitions in $\frac{k}{p}\sigma$

Fig. 4

Contribution from several spin transitions in $\frac{k}{p}\sigma$.

Fig. 5

Angular dependence of $\frac{k}{p}\frac{d\sigma }{d\textrm{cos}\,\theta }$ of the $K^- d \rightarrow p \varSigma ^-$ reaction as a function of $\textrm{cos}\theta$ (of the proton) for $\sqrt{s}=\sqrt{s}_{\textrm{th}}+10$ MeV (left) and $\sqrt{s}_{\textrm{th}}+30$ MeV (right)

We observe a smooth angular dependence, a little stronger as the energy increases, favoring backward angles. Even if the lines look parallel, there are small differences in the slope for different values of $\varLambda$. Indeed, in Fig. 5 (left), the ratio of backward to forward cross section is a factor 1.24 for $\varLambda =1250$ MeV, while it is 1.32 for 1000 MeV. The differences are bigger in Fig. 5 (right), at higher energies, where these ratios are 1.42 and 1.58 respectively. A precise measurement of the angular distributions can tell us about the value of $\varLambda$ to be used. We should also note that a difference of 125 MeV in the value of $\varLambda$ induces a change in the cross section of $16-18$% around threshold. We shall see that the deviations in the cross sections predicted by different models are of the order of a factor of two. Hence, even having a small uncertainty in the value of $\varLambda$, the measured cross sections can serve to discriminate among models.

In Fig. 6 (left), we show the contribution of each of the $\varLambda (1405)$ poles for the mechanism of Fig. 2a. As one might expect from Eq. (1), we observe that the contribution of the higher mass pole is much larger than that of the lower mass pole. However, the destructive interference between the two contributions is relevant enough to reduce the cross section in about 30%.

Fig. 6

Contributions of the high and low mass poles to the diagrams a and b in $\frac{k}{p}\sigma$

An analogous study is performed for the mechanism diagrammatically represented in Fig. 2b. Figure 6 (right) shows qualitatively similar features to the former case, but with approximately a factor ten difference in the strength of the cross section between both mechanisms. The reason for this lies in the magnifying effect of the pseudoscalar propagator produced by the fact of having a pion exchange instead of a kaon exchange. We also note that now the interference is more apparent and reduces the cross section by about 50%.

As mentioned above, the high $\varLambda ^*$ pole dominates the amplitudes. Part of the reason for the dominance of the high pole in Fig. 6 (left) is due to the fact that $g^2_{\varLambda ^*,{\bar{K}}N}$ has larger strength for the high pole than the low pole (note that the couplings are complex), but this factor is far from justifying the large difference between the two contributions in Fig. 6 (left). More significant is the case of Fig. 6 (right), the dominant term, where $g_{\varLambda ^*,{\bar{K}}N} \cdot g_{\varLambda ^*,\pi \varSigma }$ has a bigger strength for the low pole, in spite of which the high pole dominates the reaction.

In Fig. 7 (left), we show the results for each of the poles once the contributions of the two mechanisms are included in the cross section simultaneously. As before, we find the dominance of the higher $\varLambda (1405)$ pole, but the interference reduces the cross section to one half its strength.

Fig. 7

Contributions of the high and low mass poles (left) and diagrams a and b (right), compared to the total $\frac{k}{p}\sigma$

The role of each mechanism in the $K^- d \rightarrow p \varSigma ^-$ process is reflected in Fig. 7 (right) including the contribution of both poles. The results when independently taking the contributions of the two mechanisms confirm that the mechanism of Fig. 2b is the dominant one. As an interesting fact here, it should be mentioned that the addition of the mechanism of Fig. 2a to the one of Fig. 2b increases the cross section by just 10%.

So far all the results shown have been obtained employing the $\theta$-function as prescription for the deuteron wave function. Next, using Eq. (18), we swap the former prescription for the explicit wave functions derived from the Bonn and Paris potentials [73, 75]. The results are collected in Fig. 8. We observe that the cross sections obtained with either wave function are very similar, but with respect to the $\theta$ wave function they reduce the cross section by about 23%. An attempt to reduce the previous difference was carried out by rescaling the $g_d$ coupling by a factor 0.88. This works fairly well with small values of $\sqrt{s}$ but does not maintain such an accuracy as the energy increases. Because of this, all the results presented are obtained using the Bonn wave function from now on.

Fig. 8

Comparison of $\frac{k}{p}\sigma$ using the $\theta$ function or the deuteron wave functions

One can think of using other deuteron wave functions, like those based on Effective Field Theory of [76]. If one looks at Fig. 6 (left) of [76], one can see that the wave functions are very similar to the one of the Bonn Model [72]. Concretely, they are practically equivalent at distances bigger than 2 fm, indicating that the wave functions are practically the same for momentum of the deuteron smaller than 100 MeV/c, and this is the region of momenta that gives more weight to the process, since $|\varPsi (p)|^2$ at 100 MeV/c is already about 2% of $|\varPsi (p)|^2$ at the origin. One does not expect differences from using the Effective Field Theory wave functions bigger than the tiny ones in Fig. 8 between the Bonn and the Paris wave functions.

In order to illustrate the effect of the triangle singularity on the $K^- d \rightarrow p \varSigma ^-$ reaction, we find very instructive to show the corresponding amplitude. For simplicity, we have chosen the dominant spin transition $\uparrow \uparrow \rightarrow \uparrow \uparrow$ and plot the real and imaginary parts of its amplitude in the left panel of Fig. 9. Both curves behave as one might expect for a typical triangle singularity (see Fig. 5 of [17], Figs. 5, 6 of [77] and Fig. 4 of [16]). On the one hand, we see that the imaginary part (solid line) develops a smooth peak, with its highest strength around $\sqrt{s}=2380$ MeV, close to where Eq. (1) predicts the peak of the TS. The shape of the imaginary part translates information of the imaginary part of the $t_{K^- p, \pi ^+ \varSigma ^-}$ amplitude below threshold to $K^-$ energies above threshold in the $K^- d \rightarrow p \varSigma ^-$ reaction. On the other hand, the real part of the amplitude contributes largely to the strength of the cross section close to threshold. The dashed line in the same panel of Fig. 9 clearly evidences the presence of a cusp in the vicinity of the $K^- d$ threshold. To aid the visualization of this effect, we have explored a bit below threshold setting $\textbf{k}=0$ in the formulas.² These findings are in good agreement with Ref. [16, 17, 77], where it was shown that the imaginary part of the amplitude is tied to the triangle singularity, while the real part is tied to a threshold effect.

In the right panel of Fig. 9, we show the real and imaginary parts of the $t_{K^- p, \pi ^+ \varSigma ^-}$ amplitude, the one that dominates the reaction in the mechanism of Fig. 2b. As one can see in Eqs. (21, B.5), the shape of the $K^- d \rightarrow p \varSigma ^-$ amplitude is not a mapping of the one from $t_{K^- p, \pi ^+ \varSigma ^-}$. Actually, comparing both panels, it can be appreciated that the TS has created a structure of its own thereby making the amplitudes differ significantly from each other. Nevertheless, by construction, Eqs. (21, B.5) constrain the shape and strength of $t_{K^- d , p \varSigma ^-}$ to be strongly tied to that of ${\bar{K}} N \rightarrow \pi \varSigma$ amplitude. Moreover, the terms in $F'$ and $G'$ of Eq. (B.5) (Appendix B) showing explicitly the couplings of the $\varLambda (1405)$ resonances to the ${\bar{K}} N$ and $\pi \varSigma$ channels (those which are not factorized in terms of the $t_{K^- p,K^- p}$ or $t_{K^- p, \pi ^+ \varSigma ^-}$ amplitudes) give a small contribution of the order of 5% in the $K^- d \rightarrow p \varSigma ^-$ amplitudes. Therefore, this last magnitude is basically proportional to the $K^- p \rightarrow \pi ^+ \varSigma ^-$ amplitude. The fact that the two amplitudes $t_{K^- d,p \varSigma ^-}$ and $t_{K^- p, \pi ^+ \varSigma ^-}$ are so different, in spite of the approximate factorization of the latter amplitude in $t_{K^- d,p \varSigma ^-}$, is due to the extra factors in the formula of $G'$ in Eq. (B.5) which carry the information of the TS structure.

Fig. 9

Energy dependence of the real (dashed line) and the imaginary (solid line) parts of the $K^- d \rightarrow p \varSigma ^-$ for the $\uparrow \uparrow \rightarrow \uparrow \uparrow$ spin transition (left panel) and $K^- p \rightarrow \pi ^+ \varSigma ^-$ (right panel) amplitudes. The $K^- p \rightarrow \pi ^+ \varSigma ^-$ amplitude is taken from the model Oset-Ramos [35]

Finally, we analyze the impact of the $K^-p \rightarrow K^-p$, $\pi ^+ \varSigma ^-$ amplitudes from different models on the $K^- d \rightarrow p \varSigma ^-$ cross section. To this end, four models have been considered whose nature could be representative of what one can find in the literature: Oset-Ramos [35], Roca-Oset [46], Cieplý-Smejkal [48] and Feijoo-Magas-Ramos [78]. All of them are derived from a chiral SU(3) Lagrangian and implementing a unitarization scheme in coupled channels, as well as limited to s-wave projection. Despite this common approach, there are some peculiarities worth mentioning that can be useful for a future understanding of potential experimental data. We discuss the different models one by one below.

Oset-Ramos [35]: This first model uses a Weinberg–Tomozawa (WT) contribution as driving term in the interaction kernel. The authors took into account, for the first time, the full $S=-1$ meson-baryon basis for the regularization of loop integral in coupled channels.

Roca-Oset [46]: This model takes as building block the previous one, yet reducing the basis to $\pi \varLambda , \pi \varSigma , {\bar{K}}N$ channels. It has special interest for the present study because, apart from the ordinary $K^- p \rightarrow \pi \varLambda , \pi \varSigma , {\bar{K}}N$ total cross sections and threshold observables, the authors incorporated the CLAS data for the $\varLambda (1405)$ photoproduction [79] in the fits to constrain the model parameters.

Cieplý-Smejkal: The third one is the model called NLO30 in Ref. [48]. This is a model based on a chirally motivated potential, written in a separable form, whose central piece is derived from the Lagrangian up to next-to-leading order (NLO). The authors took into account in the fitting procedure the very precise measurements of the shift and width of the 1S state in kaonic hydrogen carried out by SIDDHARTA Collaboration [80].

Feijoo-Magas-Ramos: This model corresponds to the fit called WT+Born+NLO carried out in [78]. It was constructed by adding the interaction kernels derived from the Lagrangian up to NLO, and including additional experimental data at higher energies in the fits. This model is the natural extension of Oset-Ramos.

In Fig. 10, we show the Real and Imaginary parts of the amplitudes from the models that we discuss. We see that above threshold all the models basically coincide, but below threshold the different models give very different amplitudes. This means that any difference that we find for the present reaction between these models, that we discuss next, have to be attributed to the different amplitudes below threshold, indicating that the $K^- d \rightarrow p \varSigma ^-$ reaction is indeed very sensitive to this amplitude.

Fig. 10

$K^- p$ elastic amplitudes for the considered models, real part in the left panel and imaginary part in the right panel

Fig. 11

$K^- d \rightarrow p \varSigma ^-$ cross sections ($\frac{k}{p}\sigma$) for the considered models. More details in the text

In Fig. 11 we plot the resulting $K^- d \rightarrow p \varSigma ^-$ cross sections for the models discussed above. The most revealing feature in the figure is the significant difference in the cross section strength among them at small values of $\sqrt{s}$. The Oset-Ramos (dashed line) and Feijoo-Magas-Ramos (dotted line) produce almost identical results. The discrepancies become more evident when comparing the former models with Oset-Roca (dash-dotted) and Cieplý-Smejkal (dash-dot-dot line) being of the order of 40% and 100%, respectively. For low values of $\sqrt{s}$ in the $K^- d \rightarrow p \varSigma ^-$ reaction, the contributions of the ${\bar{K}}N$ amplitudes in the loop integral come mostly from ${\bar{K}}N$ invariant masses in the subthreshold region where the ${\bar{K}}N$ models present the greatest disagreements. One expects that, as the energy of the $K^-$ increases, the $\varLambda (1405)$ invariant mass, still restricted by the nucleon dynamics in the deuteron, has more access to values where all models have a better agreement among themselves because they have been fitted to the same experimental data. This effect is somewhat seen in Fig. 11 by the convergent trend shown by the models at higher energies. Roughly speaking, the process proposed in the present study acts as an indirect window to the subthreshold ${\bar{K}}N$ amplitudes that cannot only be used as a tool to discern which models are suitable to describe the physics in such a region but also may shed some light on the location of the lower mass pole of the $\varLambda (1405)$ resonance.

Fig. 12

Effects of the S- and D-wave contributions of the deuteron wave function (WF) on the $K^- d \rightarrow p \varSigma ^-$ cross section, for the dominant spin transition ($\uparrow \uparrow \rightarrow \uparrow \uparrow$) and taking into account the Oset-Ramos Model for the $S=-1$ meson-baryon amplitudes

Fig. 13

Several alternative mechanisms that can produce the $K^- d \rightarrow p \varSigma ^- \, (p \varSigma ^- \rightarrow K^- d)$ reaction: a impulse approximation, b impulse approximation with rescattering, c $\varSigma (1385)$ excitation

The calculations so far have been done using only the S-wave part of the deuteron wave function, normalized to unity, and neglecting the D-wave part, which normally provides small corrections to different observables. We have checked that this is the case here and have redone the calculations using both waves from the Bonn potential [72] for the dominant spin transition $\uparrow \uparrow$ (of $p \varSigma ^-$ system) $\rightarrow 1\,1$ ( JM of the deuteron). The details on how to account for the D-wave are given in Appendix C. In Fig. 12, we have evaluated the role of the D-wave on the cross section for $K^- d \rightarrow p \varSigma ^-$ for the dominant $\uparrow \uparrow \rightarrow \uparrow \uparrow$ transition and we find effects that range from 9% at low energies to 3% at higher energies. This effect falls well within uncertainties in our model and, most important, it is very small compared to the differences found for different models of a factor two or more.

4 Discussion

We have relied upon the mechanism for $p \varSigma ^- \rightarrow K^- d$ reaction that develops a TS, which in principle dominates over other possible mechanism where no singularity develops. The mechanism is analogous to the one of $pp \rightarrow \pi ^+d$ studied in [25] replacing pp by $p\varSigma ^-$ and the $\pi ^+$ by $K^-$. In [25], it was shown that the mechanism analogous to Fig. 2 with the $\varLambda (1405)$ replaced by the $\varDelta (1232)$ also developed a TS and reproduced very well the experimental data. Other mechanisms, like the impulse approximation, were considered therein (Ref. [25]) and they were found negligible versus the TS mechanism. This should be the case here too, but we take the opportunity to discuss other possible mechanisms which we plot in Fig. 13.

Figure 13a depicts the impulse approximation. The momentum of the $\varSigma ^-$ in this reaction for a $K^-$ at threshold is about 513 MeV/c. We have to pick up this momentum from the deuteron wave function, and taking into account the Bonn wave function [72] it has fallen by about four orders of magnitude with respect to its maximum at zero momentum. On the other hand, the $KN\varSigma$ Yukawa vertex is of the type $\mathbf {\sigma }\cdot \textbf{p}_{K^-}$ which also vanishes when the $K^-$ goes to threshold. The mechanism is completely negligible. The diagram of Fig. 13b relies upon the same mechanism but involves final state interaction. The off shellness can be split now between the deuteron and the intermediate $\varLambda , \, \varSigma$ states, softening somewhat the drastic reduction found for the mechanism of Fig. 13a. Yet, the Yukawa coupling for the near threshold $K^-$ does not give room to any relevant contribution. Finally, we show another potential mechanism depicted in Fig. 13c. This mechanism involves the $K^-N\varSigma (1385)$ vertex, which has also p-wave coupling of the type $\textbf{S}^+\textbf{p}_{K^-}$ ($\textbf{S}^+$ being the spin transition operator from spin 1/2 to spin 3/2). Once again, this mechanism has no chance to provide any appreciable contribution for the near threshold kaons that we have.

In order to further stress the role of the TS mechanism for the reaction, we consider the diagram equivalent to Fig. 2b (the one providing the largest contribution) but with a $\varLambda (1115)$ instead of the $\varLambda (1405)$. We can take advantage of the results obtained so far and start from the amplitude of Eq. (11). We obtain the contribution of the $\varLambda (1115)$ with minor changes:

• a) Replace

  $$\begin{aligned} g_{\varLambda ^*,K^-p} \cdot g_{\varLambda ^*,\pi ^+\varSigma ^-} \rightarrow \bigg (\frac{2}{\sqrt{3}}\frac{D}{2f}\mathbf {\sigma }\textbf{k}+\frac{1}{\sqrt{3}}\frac{-D-3F}{2f}\mathbf {\sigma }\textbf{q}\bigg )\nonumber \\ \end{aligned}$$

  (22)

• b) Replace

  $$\begin{aligned} E_{\varLambda ^*} - i\frac{\varGamma _{\varLambda ^*}}{2} \rightarrow E_{\varLambda } \end{aligned}$$

  (23)

The replacement in point a) naturally brings to re-express $W_{ij} \rightarrow W^{'}_{ij}=\langle j |\mathbf {\sigma }^{(1)}\textbf{q}\mathbf {\sigma }^{(2)}\textbf{k}\mathbf {\sigma }^{(2)}\textbf{q}| i\rangle$. Again we evaluate that for the most important transition, namely $\uparrow \uparrow \rightarrow \uparrow \uparrow$ where

$$\begin{aligned} W^{'}_{11}(q)=q_z\big [ \textbf{k}\cdot \textbf{q}+i(k_xq_y-k_yq_x)\big ]. \end{aligned}$$

(24)

The results for the cross sections are shown in Fig. 14. We observe that in the region close to threshold where the TS shows up the contribution is about four orders of magnitude smaller. One of the reasons is that the $\varLambda \rightarrow K^- p$ coupling involves a p-wave which rapidly decreases close to threshold. In fact, in the plot, we observe that the new contribution is only about one fourth of the one coming from TS at larger energies. One can completely ignore this mechanism in the TS region and so can we say of other intermediate states like the $\varSigma (1197)$, $\varSigma ^*(1385)$ or $\varLambda (1520)$ (d-wave).

One can also ask about the possible role of initial or final state interaction of the $K^- d \rightarrow p \varSigma ^-$ reaction. The initial state interaction with $K^-$ interacting with the nucleons of the deuteron is dominated by the high $\varLambda ^*$ resonance at 1426 MeV and has already been taken into account. The final state interaction of the $p\varSigma ^-$ deserves some comment. This interaction is relevant when the kinetic energy of the system is small compared with the $p\varSigma ^-$ potential. Here the kinetic energy is large, $m_K+m_d-m_p-m_\varSigma =236.5$ MeV, much larger than the average $p\varSigma ^-$ potential. One can get a feeling of the situation by taking the $p\varSigma ^-$ scattering length most suited to our problem with $I=1/2$ and spin triplet, $a=2.61-i2.89$ fm [81]. This is small compared to the np $I=0$ spin triplet of the deuteron, $a=5.38$ fm which barely binds the deuteron by 2.2 MeV. Another indication is given by the binding of $\varSigma ^-$ in nuclei. The strong interaction from fits to pionic atoms results in an attractive potential $\varSigma ^-$-nucleus of about 30 MeV coming from the interaction of the $\varSigma ^-$ with all nucleons of the nucleus within the range of the interaction [82, 83]. Assuming a few nucleons contributing to this potential, the magnitude obtained for the $p\varSigma ^-$ potential is very small compared to the 236.5 MeV of kinetic energy of the $p\varSigma ^-$ system here, which allows us to ignore the contribution of the final state interaction.

Fig. 14

Comparison between the contributions to the $K^-d\rightarrow p\varSigma ^-$ total cross section from the mechanism depicted in Fig. 2b and the analogous one with $\varLambda (1115)$ in the triangle topology instead for the $\uparrow \uparrow \rightarrow \uparrow \uparrow$ spin transition. See more details in the text

Fig. 15

Mechanisms considered in Refs. [45, 46, 84]

It is also interesting to put the new reaction in perspective to see what can we gain from its observation. The point in the conclusions is that one can learn about the ${\bar{K}} N$ interaction below threshold where the theoretical models still differ significantly.

Ideally, it would be good to parametrize the amplitudes in terms of subthreshold parameters such as pole positions in the complex plane and residues at the poles, and use the data to obtain those parameters. This is actually one of the options that we have used in the present study (see solid line in Fig. 11). Yet, this is not sufficient, as this parametrization is valid only in the proximity of the poles, and the use of the full amplitudes produces the differences that we observe in Fig. 11, comparing the solid and the dashed line. On the other hand, the information on these subthreshold parameters requires, using only the $\bar{K}N$ and $\pi \varSigma$ channels, 2 complex poles, 2 complex couplings for each resonance to each of these channels, in total 12 parameters, as one can see in Table 1. Conversely, one can see the amount of free parameters in the different recent theories, which is around 15 (16 in the model of Ref. [78]). It is clear from the shape of the predictions for the cross section in Fig. 11 that the data does not contain enough information to determine all these parameters, since it is easy to parametrize it in terms of about 3 parameters for a parabola shape, for example. In any case, one is very far away from the 12 to 16 parameters that we would need to determine the amplitudes below threshold. It is thus clear that the information obtained from the present reaction is partial and has to be added to other information obtained from different reactions. Yet, we have proved that the reaction is very sensitive to the subthreshold amplitudes by comparing different models and, hence, should play a relevant role in determining these amplitudes, when added to the information from other reactions. In this sense, we discuss below the complementary reactions that globally could help us to determine these amplitudes.

One source of information comes from the study of photonuclear $\gamma p \rightarrow K^+ \pi \varSigma$ reactions [79], which were studied theoretically in Refs. [45, 46, 84] and allowed to obtain important information concerning the two $\varLambda (1405)$ states. The mechanisms considered in this latter papers are depicted in Fig. 15. As can be seen from this figure, one can test the $\pi \varSigma \rightarrow \pi \varSigma$ and the ${\bar{K}} N \rightarrow \pi \varSigma$ amplitudes below the ${\bar{K}} N$ threshold in the region of the two $\varLambda (1405)$ states. If we compare, these mechanisms with those of Fig. 2, we see that in addition we have here the mechanism of Fig. 2a which involves the $K^- p \rightarrow K^- p$ amplitude, which, depending on the model, can give different contributions, although we found here that the contribution of this diagram is relatively small. On the other hand, in the photonuclear reaction (see Fig. 15) one has three particles in the final state, and the mass distribution of the $\pi \varSigma$ system spreads around in a long range since it depends on the $K^+$ momentum. By contrary, the mechanisms of Fig. 2, due to the TS, are more selective to the configuration that places the $\varLambda$ on shell. It was also found in [45, 46] that both $\varLambda ^*$ resonances contributed to the reaction, with different weight depending on the photon energy, while here our process is dominated by the high $\varLambda ^*$ pole. In summary, one collects complementary information from both reactions.

Fig. 16

Mechanism for the $K^-p \rightarrow \pi ^0 \pi ^0 \varSigma ^0$ reaction

Related to this reaction we can also mention the $K^- p \rightarrow \pi ^0 \pi ^0 \varSigma ^0$ reaction measured in [85] and studied theoretically in [41] by means of the mechanism depicted in Fig. 16, where the $\varLambda (1405)$ is excited in spite of using kaon beams with $K^-p$ (initial) above threshold.

Fig. 17

Feynman diagram for the process ${\bar{\nu }}_lp \rightarrow l^+\phi B$

Similarly, the ${\bar{\nu }}$ induced $\varLambda (1405)$ production, studied theoretically in [86] and schematically represented in Fig. 17, will also bring information on the $\varLambda (1405)$, and hence on $\bar{K} N$ subthreshold amplitude below threshold. This latter reaction is one of the possible output of the MicroBooNE collaboration, where $\varLambda$, $\varSigma$ and related hyperons production is presently under analysis.³ In addition, it is expected that SBND will be able to measure such processes with huge statistics.

A different source of information comes from the $K^-d \rightarrow \pi \varSigma N$ reaction [87, 88] studied theoretically in Refs. [89,90,91,92]. The basic mechanism for this reaction is depicted in Fig. 18. The reaction starts from a fast $K^-$ (around 1 GeV/c) which loses its energy upon collision with a neutron of the deuteron, and the resulting $K^-$ interacts with a proton to give $\pi \varSigma$.⁴ We only have the $K^-p \rightarrow \pi \varSigma$ amplitude at low energies and not the $K^-p \rightarrow K^-p$ and, similarly to what happens in the photoproduction case, we have three particles in the final state and the same $\pi \varSigma$ invariant mass can be obtained from different configurations of the n. Once again we see that the reaction studied here and the $K^-d \rightarrow \pi \varSigma N$ one provide complementary information to our knowledge of the ${\bar{K}} N \rightarrow \pi \varSigma$ and ${\bar{K}} N \rightarrow {\bar{K}} N$ amplitudes below threshold.

Fig. 18

Mechanism for the $K^-d \rightarrow \pi \varSigma N$ reaction

5 Conclusions

We have investigated the $p \varSigma ^- \rightarrow K^- d$ and its time reversal $K^- d \rightarrow p \varSigma ^-$ reactions, which are driven by a triangle mechanism with the $\varLambda (1405)$, a proton and a neutron in the intermediate states. We show that the triangle mechanism develops a triangle singularity which magnifies the cross section and produces a particular shape in the cross section. We show analytically that in the case of a narrow $\varLambda (1405)$ width, a TS appears a few MeV above threshold, and this peak becomes broader upon consideration of the $\varLambda (1405)$ width. We could show that of the mechanisms involving a $\pi$ or K exchange, the one involving the $\pi$ exchange is the dominant one, and of the two $\varLambda (1405)$ resonances, the one of higher mass gives also the largest contribution. We showed, from the analytical expression of the transition amplitude, that it was weighting the $K^- p \rightarrow \pi ^+ \varSigma ^-$ amplitude below threshold with a particular configuration tied to the TS which produced a shape quite distinct from the one of the $K^- p \rightarrow \pi ^+ \varSigma ^-$ amplitude. This dependence on the ${\bar{K}} N$ and $\pi \varSigma$ amplitude below threshold makes this reaction quite sensitive to different models that, giving similar cross sections for ${\bar{K}} N$ reactions above threshold, produce rather different extrapolations of the ${\bar{K}} N$ amplitudes below threshold. This information is relevant in the issue of ${\bar{K}}$ bound states in nuclei [94,95,96]. Thus, the measurement of this reaction will provide new and valuable information concerning this problem. On the other hand, with regard to the two poles of the $\varLambda (1405)$, one around 1420 MeV and the other one around 1385 MeV, while practically all theoretical models coincide on the features of the $\varLambda (1420)$, they differ substantially in the position and width of the lower mass one. The new information provided by this reaction will help to narrow the predictions around the second state.

Concerning the feasibility of the experiment, two lines emerge as good candidates. The Kaon beam of JPARC can be used, and even counting the low rates of low energy kaons, the experiment can be carried out.⁵ Another possibility is to photoproduce the $\varSigma ^-$ at Jefferson Lab and do the $\varSigma ^- p \rightarrow K^- d$ reaction. The $\varLambda p \rightarrow \varLambda p$ reaction with this technique has been successfully tested [97], but higher statistic samples than the present one would be needed.⁶

Appendices

Appendix A: Spin matrix elements $V_{ij}$ and $W_{ij}$.

The $\mathbf {\sigma }\cdot \textbf{q}$ product is expressed as:

$$\begin{aligned} \mathbf {\sigma }\cdot \textbf{q}=\sigma _+ q_- + \sigma _- q_+ + \sigma _z q_z \end{aligned}$$

(A.1)

with

$$\begin{aligned} q_+= & {} q_x + \mathrm{i\,}q_y \nonumber \\ q_-= & {} q_x - \mathrm{i\,}q_y \nonumber \\ \sigma _+= & {} \frac{1}{2}(\sigma _x + \mathrm{i\,}\sigma _y) \nonumber \\ \sigma _-= & {} \frac{1}{2}(\sigma _x - \mathrm{i\,}\sigma _y). \end{aligned}$$

(A.2)

Then, the elements of the spin-transition matrix for a couple of incoming $\frac{1}{2}$-baryons (p and $\varSigma ^-$, in this case) going to the constituent pair of nucleons merged in the deuteron (S=1) can be written in the following form.

Accounting for mechanism (a) in Eq. (11)), $V_{ij}$:

$$\begin{aligned} \uparrow \uparrow \rightarrow \uparrow \uparrow : \;\;\;\; V_{11}= & {} q_z \nonumber \\ \uparrow \uparrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; V_{12}= & {} \frac{1}{\sqrt{2}}q_+ \nonumber \\ \uparrow \uparrow \rightarrow \downarrow \downarrow : \;\;\;\; V_{13}= & {} 0 \nonumber \\ \uparrow \downarrow \rightarrow \uparrow \uparrow : \;\;\;\; V_{21}= & {} q_- \nonumber \\ \uparrow \downarrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; V_{22}= & {} -\frac{1}{\sqrt{2}}q_z \nonumber \\ \uparrow \downarrow \rightarrow \downarrow \downarrow : \;\;\;\; V_{23}= & {} 0 \nonumber \\ \downarrow \uparrow \rightarrow \uparrow \uparrow : \;\;\;\; V_{31}= & {} 0 \nonumber \\ \downarrow \uparrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; V_{32}= & {} \frac{1}{\sqrt{2}}q_z \nonumber \\ \downarrow \uparrow \rightarrow \downarrow \downarrow : \;\;\;\; V_{33}= & {} q_+ \nonumber \\ \downarrow \downarrow \rightarrow \uparrow \uparrow : \;\;\;\; V_{41}= & {} 0 \nonumber \\ \downarrow \downarrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; V_{42}= & {} \frac{1}{\sqrt{2}}q_- \nonumber \\ \downarrow \downarrow \rightarrow \downarrow \downarrow : \;\;\;\; V_{43}= & {} -q_z \nonumber \\ \end{aligned}$$

(A.3)

Accounting for mechanism (b) in Eq. (11)), $W_{ij}$:

$$\begin{aligned} \uparrow \uparrow \rightarrow \uparrow \uparrow : \;\;\;\; W_{11}= & {} q_z \nonumber \\ \uparrow \uparrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; W_{12}= & {} \frac{1}{\sqrt{2}}q_+ \nonumber \\ \uparrow \uparrow \rightarrow \downarrow \downarrow : \;\;\;\; W_{13}= & {} 0 \nonumber \\ \uparrow \downarrow \rightarrow \uparrow \uparrow : \;\;\;\; W_{21}= & {} 0 \nonumber \\ \uparrow \downarrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; W_{22}= & {} \frac{1}{\sqrt{2}}q_z \nonumber \\ \uparrow \downarrow \rightarrow \downarrow \downarrow : \;\;\;\; W_{23}= & {} q_+ \nonumber \\ \downarrow \uparrow \rightarrow \uparrow \uparrow : \;\;\;\; W_{31}= & {} q_- \nonumber \\ \downarrow \uparrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ): \;\;\;\; W_{32}= & {} -\frac{1}{\sqrt{2}}q_z \nonumber \\ \downarrow \uparrow \rightarrow \downarrow \downarrow : \;\;\;\; W_{33}= & {} 0 \nonumber \\ \downarrow \downarrow \rightarrow \uparrow \uparrow : \;\;\;\; W_{41}= & {} 0 \nonumber \\ \downarrow \downarrow \rightarrow \frac{1}{\sqrt{2}}(\uparrow \downarrow +\downarrow \uparrow ):\;\;\;\; W_{42}= & {} \frac{1}{\sqrt{2}}q_- \nonumber \\ \downarrow \downarrow \rightarrow \downarrow \downarrow : \;\;\;\; W_{43}= & {} -q_z \nonumber \\ \end{aligned}$$

(A.4)

Appendix B: $F'$ and $G'$ functions.

As shown below, in order to factorize the $t_{l,m}$ amplitudes, the mass and width of the heavier resonance at 1426 MeV are taken in the terms $(P^0-E_{\varLambda ^*}(\textbf{P}-\textbf{q})-\omega _K(q)+i\frac{\varGamma _{\varLambda ^*}}{2})^{-1}$ of $F'$ and $(P'^0-E_{\varLambda ^*}(-\textbf{P}-\textbf{q})-\omega _\pi (q)+i\frac{\varGamma _{\varLambda ^*}}{2})^{-1}$ of $G'$. This can be done because these terms are very small compared to the other terms in the same bracket and this resonance is the one giving the largest contribution.

The $F'$ and $G'$ functions in Eq. (21) are defined as:

$$\begin{aligned}&F'(P^0,P'^0,\textbf{q},\omega _K,\textbf{P},\textbf{k})=\frac{1}{2\omega _K(\textbf{q})}\nonumber \\&\quad \frac{M_N}{E_N(\textbf{P}-\textbf{q}-\textbf{k})}\frac{M_N}{E_N(-\textbf{P}+\textbf{q})}\nonumber \\&\quad \frac{1}{\sqrt{s}-k^0-E_N(-\textbf{P}+\textbf{q})-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\&\times \left\{ \sum _{i=1,2}\frac{M_{\varLambda ^*}^{(i)}}{E_{\varLambda ^*}^{(i)}(\textbf{P}-\textbf{q})}\frac{(g^{(i)}_{\varLambda ^*,K^-p})^2}{P^0-\omega _K(\textbf{q})-E^{(i)}_{\varLambda ^*}(\textbf{P}-\textbf{q})+i\frac{\varGamma _{\varLambda ^*}^{(i)}}{2}}\right. \nonumber \\&\quad \left. \frac{1}{P^0-\omega _K(\textbf{q})-k^0-E_N(\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\right. \nonumber \\&\quad +\left. \left( \frac{1}{P^0-E_{\varLambda ^*}(\textbf{P}-\textbf{q})-\omega _K(\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\right. \right. \nonumber \\&\quad \left. \left. +\frac{1}{P'^0-E_N(-\textbf{P}+\textbf{q})-\omega _K(\textbf{q})+i\epsilon }\right) t_{K^-p,K^-p}(M_\textrm{inv})\right\} ,\nonumber \\&G'(P^0,P'^0,\textbf{q},\omega _\pi ,\textbf{P},\textbf{k})=\frac{1}{2\omega _\pi (\textbf{q})}\frac{M_N}{E_N(-\textbf{P}-\textbf{q}-\textbf{k})}\nonumber \\&\quad \frac{M_N}{E_N(\textbf{P}+\textbf{q})}\frac{1}{\sqrt{s}-k^0-E_N(\textbf{P}+\textbf{q})-E_N(-\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\nonumber \\&\times \left\{ \sum _{i=1,2}\frac{M_{\varLambda ^*}^{(i)}}{E_{\varLambda ^*}^{(i)}(-\textbf{P}-\textbf{q})}\frac{g^{(i)}_{\varLambda ^*,K^-p}g^{(i)}_{\varLambda ^*,\pi ^+\varSigma ^-}}{P^0-\omega _\pi (\textbf{q})-E^{(i)}_{\varLambda ^*}(-\textbf{P}-\textbf{q})+i\frac{\varGamma _{\varLambda ^*}^{(i)}}{2}}\right. \nonumber \\&\quad \left. \frac{1}{P'^0-\omega _\pi (\textbf{q})-k^0-E_N(-\textbf{P}-\textbf{q}-\textbf{k})+i\epsilon }\right. \nonumber \\&\left. \quad +\left( \frac{1}{P'^0-E_{\varLambda ^*}(-\textbf{P}-\textbf{q})-\omega _\pi (\textbf{q})+i\frac{\varGamma _{\varLambda ^*}}{2}}\right. \right. \nonumber \\&\left. \left. \quad +\frac{1}{P^0-E_N(\textbf{P}+\textbf{q})-\omega _\pi (\textbf{q})+i\epsilon }\right) t_{K^-p,\pi ^+\varSigma ^-}(M'_\textrm{inv}) \ \right\} ,\nonumber \\ \end{aligned}$$

(B.5)

with $M^2_\textrm{inv}=s+M^2_N-2\sqrt{s}E_N(-\textbf{P}+\textbf{q})$ and $M'^2_\textrm{inv}=s+M^2_N-2\sqrt{s}E_N(\textbf{P}+\textbf{q})$.

Appendix C: D-wave contribution.

We show here how to evaluate the contribution of the deuteron D-wave function. Following Appendix C of Ref. [72], we have for the deuteron wave function

$$\begin{aligned} \varphi _d^M(\textbf{p})=\left[ \psi _0(p){\mathcal {Y}}_{01}^{1M}({\hat{p}})+\psi _2(p){\mathcal {Y}}_{21}^{1M}({\hat{p}})\right] \end{aligned}$$

(C.6)

where ${\mathcal {Y}}_{LS}^{JM}({\hat{p}})$ are the angular-spin wave functions of the two nucleons with orbital angular momentum L, spin S, and total angular momentum J with projection M.

$$\begin{aligned} {\mathcal {Y}}_{LS}^{JM}({\hat{p}})=\sum _{m} \mathcal{C}(LSJ;m,M-m)Y_{Lm}({\hat{p}}) |S,M-m\rangle \nonumber \\ \end{aligned}$$

(C.7)

we evaluate the matrix element for the transition $\uparrow \uparrow \rightarrow 1\,1$ (JM) which is the dominant one. We have

$$\begin{aligned} \psi _2 (p) {\mathcal {Y}}_{21}^{11}({\hat{p}})&=\psi _2 (p)\left\{ \sqrt{\frac{3}{5}}Y_{22}({\hat{p}})|1,-1\rangle - \sqrt{\frac{3}{10}}Y_{21}({\hat{p}})|1,0\rangle \right. \nonumber \\&\quad + \left. \sqrt{\frac{1}{10}}Y_{20}({\hat{p}})|1,1\rangle \right\} \nonumber \\&= \psi _2 (p)\left\{ \sqrt{\frac{3}{5}}Y_{22}({\hat{p}}) \downarrow \downarrow - \sqrt{\frac{3}{10}}Y_{21}({\hat{p}})\right. \nonumber \\&\quad \left. \sqrt{\frac{1}{2}} (\uparrow \downarrow + \downarrow \uparrow ) + \sqrt{\frac{1}{10}}Y_{20}({\hat{p}})\uparrow \uparrow \right\} ,&\end{aligned}$$

(C.8)

where in the first part of the equation the $|S,M_S\rangle$ spin states are written and in the second part they are expressed in terms of $|s_1,s_2\rangle$ of the nucleon spin projections. The transition from the initial state $\uparrow \uparrow$ to the final $1\,1$ (JM) in D-wave for the mechanism (a) is readily evaluated using Eqs. (A3), and the $V_{ij}$ magnitude is replaced by

$$\begin{aligned} {\widetilde{V}}=\sqrt{\frac{1}{10}} Y_{20}({\hat{p}}) q_z -\sqrt{\frac{3}{10}} Y_{21}({\hat{p}}) \sqrt{\frac{1}{2}} q_+ \end{aligned}$$

(C.9)

where

$$\begin{aligned} \textbf{p}=\textbf{P}-\textbf{q}-\frac{\textbf{k}}{2} \end{aligned}$$

(C.10)

with the momenta $\textbf{P}, \textbf{q}, \textbf{k}$ defined after Eq. (16).

We find

$$\begin{aligned} Y_{21}({\hat{p}})= & {} \sqrt{\frac{15}{8\pi }} \frac{\sin {\tilde{\theta }}\cos {\tilde{\theta }}}{|\textbf{p}|} \left\{ (\textbf{q}+\frac{\textbf{k}}{2})_x +i (\textbf{q}+\frac{\textbf{k}}{2})_y \right\} \nonumber \\ Y_{20}({\hat{p}})= & {} \sqrt{\frac{5}{4\pi }}\left( \frac{3}{2} \cos ^2{\tilde{\theta }} -\frac{1}{2} \right) \end{aligned}$$

(C.11)

where

$$\begin{aligned} \cos {\tilde{\theta }}=\frac{P-q\cos \theta -\frac{k}{2}\cos \theta _k}{|\textbf{p}|} \, . \end{aligned}$$

(C.12)

Hence, to include the $\uparrow \uparrow \rightarrow 11$ D-wave contribution, we must do the replacement

$$\begin{aligned}&-(2\pi )^{3/2}\psi (\textbf{p})q_z \rightarrow -(2\pi )^{3/2}\nonumber \\&\left\{ w_s\psi (p) q_z +\psi _2(p) \left[ \sqrt{\frac{1}{10}} Y_{20}({\hat{p}}) q_z -\sqrt{\frac{3}{10}} Y_{21}({\hat{p}}) \sqrt{\frac{1}{2}} q_+\right] \right\} , \end{aligned}$$

(C.13)

where $\psi (p)$ is the wave function of Eq. (18), which already includes the $Y_{00}$ spherical harmonic, and where $w_s^2$ stands for the S-wave probability with $w_s=0.9752$. The same holds for the $\uparrow \uparrow \rightarrow 11$ transition of the mechanism (b), since for the $\uparrow \uparrow$ initial state the three $W_{ij}$ matrix elements are the same as $V_{ij}$, but now $\textbf{p}=-\textbf{P}-\textbf{q}-\frac{\textbf{k}}{2}$.

We take advantage to mention that in Ref. [72] the deuteron wave functions in coordinate space and momentum space given by Eqs. (C19) and (C21) respectively for s-wave are correct, the one of the d-wave of Eq. (20) corresponds indeed to the results of Table XIX, but the formula of Eq. (22) for d-wave in momentum space, should be changed of sign.⁷ We have followed this latter prescription.