Abstract
MnO thin films with various thicknesses and strains were grown on MgO substrates by pulsed laser deposition technique, then characterized using x-ray diffraction and infrared reflectance spectroscopy. Films grown on (0 0 1)-oriented MgO substrates exhibit homogenous biaxial compressive strain which increases as the film thickness is reduced. For that reason, in paramagnetic phase, the frequency of doubly-degenerate phonon increases with the strain, and splits below Néel temperature TN due to the magnetic-exchange interaction. The phonon splitting in the MnO (0 0 1) films is 20% larger than that of the bulk MnO. Films grown on (1 1 0)-oriented MgO substrates exhibit a huge phonon splitting already at room temperature due to the anisotropic in-plane compressive strain. Below TN, the lower-frequency phonon splits in the IR spectra and the higher-frequency phonon strongly hardens in AFM phase; these features are evidences for a spin-order-induced structural phase transition from tetragonal to a lower symmetry phase. Total phonon splitting is 55 cm−1 in (1 1 0)-oriented MnO film, which is more than twice the value in bulk MnO, but since the splitting is present already in paramagnetic phase, we cannot clearly correlate it with the value of exchange coupling constant. Nevertheless, at least observation of enhanced phonon splitting in strained MnO (0 0 1) films show that the exchange coupling could be enhanced by the compressive strain which supports recent theoretical predictions published by Wan et al (2016 Sci. Rep. 6 22743) and Fischer et al (2009 Phys. Rev. B 80 014408).
Export citation and abstract BibTeX RIS
1. Introduction
Magnetic ordering can affect the lattice dynamics of strongly-correlated electronic systems This phenomenon can yield phonon anomalies or even splitting of phonons below the Néel temperature TN in various antiferromagnets [1–4]. Phonon anomalies have also been observed near TN in most multiferroics (regardless of whether they are type I or type II) [5–7]. Coupling of polar phonons with spin waves is also responsible for activation of electrically active magnons (called electromagnons) in the terahertz dielectric spectra of multiferroics [8, 9].
A huge degree (up to 10%) of phonon splitting can occur in magnetic binary oxides at the onset of magnetic alignment [1–3]. It motivated the researchers to investigate the origin of this phenomenon in more details. The magnetic-order-induced phonon splitting in manganese monoxide MnO was first predicted theoretically and ab initio calculation showed a substantial spin-order-induced anisotropy for the Born effective charge tensor and thus for the zone-center optic phonons [10]. This work suggested the phenomenon of solely magnetically-induced phonon splitting; several subsequent theoretical studies attempted to explain the nature of spin-phonon coupling in detail. Anisotropic magnetic coupling due to the non-cubic distribution of the spin density can produce a splitting of transversal optical phonons during the superexchange interaction in MnO and NiO [11]. The degree of phonon splitting increases linearly with increase in the non-dominant magnetic exchange interaction J1 in transition-metal monoxides and in frustrated antiferromagnetic (AFM) oxide spinels [3].
Phonon splitting must be a consequence of a decrease in crystal symmetry below TN. At room temperature (RT), MnO crystalizes in the cubic rocksalt structure (space group Fm m), with lattice parameter of 4.445 Å [12]. At TN = 118 K, MnO transforms from paramagnetic to AFM phase. In the AFM structure the magnetic moments are arrayed in ferromagnetic sheets parallel to (1 1 1) planes, and the direction of magnetization in neighboring planes is antiparallel [13]. The low-temperature crystal structure of MnO is a matter of debate; it seems to undergo spin-order-induced symmetry lowering to rhombohedral structure [12–15], but structural investigations of AFM phase using neutron diffraction revealed a monoclinic crystal structure with the acentric space group C2 [16] or centrosymmetric C2/m [17]. Even the high-temperature cubic structure of MnO has been questioned, because new high-resolution synchrotron radiation studies revealed tetragonal structure with the space group I4/mmm [18]. This structure is rather plausible, because it has group-subgroup relation with the monoclinic structure that is observed below TN.
m), with lattice parameter of 4.445 Å [12]. At TN = 118 K, MnO transforms from paramagnetic to AFM phase. In the AFM structure the magnetic moments are arrayed in ferromagnetic sheets parallel to (1 1 1) planes, and the direction of magnetization in neighboring planes is antiparallel [13]. The low-temperature crystal structure of MnO is a matter of debate; it seems to undergo spin-order-induced symmetry lowering to rhombohedral structure [12–15], but structural investigations of AFM phase using neutron diffraction revealed a monoclinic crystal structure with the acentric space group C2 [16] or centrosymmetric C2/m [17]. Even the high-temperature cubic structure of MnO has been questioned, because new high-resolution synchrotron radiation studies revealed tetragonal structure with the space group I4/mmm [18]. This structure is rather plausible, because it has group-subgroup relation with the monoclinic structure that is observed below TN.
In high-temperature cubic structure, only one triple-degenerate optical phonon with symmetry F1u should be infrared (IR) active [2]. The symmetry permits no Raman or silent mode. If the paramagnetic structure is tetragonal [18], the F1u phonon should split in two components A2u and Eu, and both modes should be also IR active. Room-temperature IR reflectivity spectra of MnO bulk samples revealed two reflection bands; the high-frequency mode near 410 cm−1 was explained by a multiphonon absorption [2, 19, 20], so only the peak near 270 cm−1 indicates an optical phonon in the paramagnetic phase; this observation supports the hypothesis of cubic symmetry. Nevertheless, finite phonon damping occurs, so one cannot exclude a small phonon splitting due to small (10−4) [18] tetragonal distortion, which cannot be revealed in the IR spectra. Inelastic neutron scattering revealed 10% phonon splitting in doublet below TN [21], and IR reflectivity even found splitting into three components [1–3]; these observations support lower than tetragonal symmetry in AFM phase. Based on theoretical papers [10, 22], Kant et al [3] claimed that 'The pure lattice contributions due to deviations from the cubic symmetry in the magnetically ordered state were estimated in the case of MnO and NiO to be less than 1% of the phonon eigenfrequencies, while the exchange-driven and experimentally observed splittings are one order of magnitude larger'. Nevertheless, the crystal symmetry lowering observed below TN is induced by magnetic interactions and the same interactions (described by J1) are responsible for phonon splitting in AFM phase. It means the observed 10% phonon splitting must be in agreement with lattice distortion below TN and actually theoretical papers [10, 22] claim the same.
Using an ab initio study, Fischer et al [23] calculated the effect of hydrostatic pressure on the nearest neighbor magnetic interaction in transition metal monoxides. They showed that J1 in MnO substantially increases as a function of pressure. Subsequent theoretical study of Wan et al [24] has predicted that also compressive biaxial strain can increase magnetic exchange interaction, and thereby 4% compressive strain can induce ferroelectric order in the AFM phase of thin MnO film. This study proposed a completely new mechanism for preparation of strain-induced multiferroics. Epitaxial strain has been already used to induce ferroelectricity in quantum paraelectric SrTiO3 [25] or in antiferromagnets with large spin-phonon coupling (EuTiO3 and SrMnO3) [6, 26], but in all of these materials the ferroelectric phase transition is of displacive type, i.e. driven by a polar soft phonon. Moreover, in strained EuTiO3, the AFM order changes to ferromagnetic order under strain, so high magnetoelectric coupling is expected in this type-I multiferroic material. In type-II multiferroics, the ferroelectric polarization can be induced by a special spin order, as has been observed in many magnetic materials (e.g. review [27]), but spin-order induced multiferroicity under epitaxial strain has been predicted only in MnO, because exchange coupling constant J1 is anomalously large and highly sensitive on pressure or strain [23, 24]. Considering the experimental observation of Kant et al [3] one expects to see a substantial increase of phonon splitting under compressive strain, because there is a linear dependence between the degree of splitting and non-dominant exchange coupling constant J1.
The aim of this article is to study the influence of the strain and AFM ordering on lattice dynamics in MnO thin films. The phonons are IR active and IR reflectance spectroscopy is highly sensitive to polar phonons in ultrathin films [28], so we use this technique between 10 and 300 K.
2. Experimental details
To apply different level of strain in various directions in MnO, MgO single crystals (Crystech) oriented in 0 0 1 and 1 1 0 directions were selected as the substrates in this research. All substrates were cleaned ultrasonically in acetone and methanol for 10 min in each to remove the contaminations from the top surface. After drying under a high purity nitrogen gas flow, the annealing process was carried out according to the table 1, to prepare atomically smoothed surface [29]. After several attempts we realized that 1150 °C is the most proper temperature to control the surface treatment of MgO (0 0 1) substrate and 950 °C for MgO (1 1 0). In case of MgO (1 1 0), we reduced the annealing temperature as the surface is more active (less atomic density) and higher annealing temperatures makes the treatment process out-of-control resulting in a rough surface. The more detailed explanation is available in [29].
Table 1. Annealing conditions for MgO substrates with different orientations (performed before film depositions).
| Substrate | Atmosphere | Temperature | Time |
|---|---|---|---|
| MgO (0 0 1) | Air | 1150 °C | 3 h |
| MgO (1 1 0) | Air | 950 °C | 3 h |
A MnO ceramic pellet (99.99%) was used as a target for pulsed laser deposition (PLD) of all thin films. A KrF pulsed laser (λ = 248 nm) with a repetition rate of 10 Hz was operated to ablate the ceramic pellet. During the deposition process, the substrate was heated to 650 °C, which is the optimal temperature to grow MnO films of highest quality [29]. A detailed study on the pulsed laser deposition of MnO film on MgO substrate showed that below 650 °C the deposited film contained higher oxidized phase like Mn3O4 [29]. The films grown at higher temperatures do not present high-quality surface (ω rocking curve around the (0 0 2) Bragg peak (not shown) revealed a single broad peak indicating a mosaic structure) which can affects the IR spectra in a negative way. The MnO films were grown under vacuum of 10−6 Torr. The laser beam was focused on the target surface through an optical lens at a fluence 1 ⩽ F ⩽ 2 J cm−2. The substrate was placed 50 mm above the target. MnO films with thicknesses from 17 nm to 65 nm were deposited, then at the end of deposition process, the chamber was immediately cooled to RT at 10 °C min−1 under the growth condition.
The phases of the films and their crystal quality were evaluated using an x-ray diffractometer with a copper source operating at 40 V and 200 mA, followed by a theta rocking scan around the detected MnO Bragg peaks. An x-ray reflectometry technique was used to determine the film thickness (accuracy mostly ± 0.3 nm). Moreover, x-ray diffraction studies to determine film thicknesses, strain and lattice parameters of MnO grown on MgO (1 10) substrate were performed using a Bruker D8 Discover equipped with rotating Cu anode (λ(CuKα1) = 1.540 598 Å; λ(CuKα2) = 1.544 426 Å) working with 12 kW power. A parabolic Göbel mirror was located on the side of the incident beam. Analyzer Soller slits, analyzer crystal (2 0 0-LiF) or dual analyzer 'Pathfinder' were used on the side of the diffracted beam. The out-of-plane lattice parameter d1 1 0 was obtained using a symmetrical 2θ/θ scan; d1 0 0 and d0 1 0 lattice parameters were obtained using inclined (χ = 45°) symmetrical 2θ/θ scans. The d0 0 1 lattice parameter was found using a reciprocal space map (RSM) of the 2 2 4 diffraction.
The IR reflectivity measurements were performed using a Bruker IFS 113v Fourier transform IR spectrometer equipped with a helium-cooled (1.6 K) silicon bolometer. Spectra were measured at temperatures from 10 to 300 K, which were maintained using an Oxford Optistat CF cryostat with 3 mm-thick polyethylene windows transparent up to 650 cm−1. RT spectra were taken up to 4000 cm−1. Polarized and unpolarized reflectance measurements were performed in near-normal incidence geometry. Metal mesh deposited on 6 µm-thick mylar was used as a polarizer.
3. Results and discussion
3.1. X-Ray diffraction analysis
Out-of plane lattice constant, strain, thickness and sample homogeneity of all thin films were determined using XRD at 300 K. In-plane strain and lattice parameters of two MnO(1 1 0) films with thicknesses 26.5 ± 0.3 nm and 18 ± 1 nm were also measured.
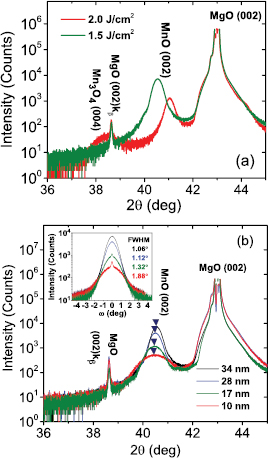
Fluence of the laser affected the XRD patterns of films (figure 1(a)). As fluence was increased to 2 J cm−2, a second phase (Mn3O4) emerged, possibly because the increased energy effected the ionization of Mn atoms. Pure MnO phase was obtained by reducing fluence below1.5 J cm−2. As film thickness was decreased, the 2θ angle of the MnO 0 0 2 peak decreased (figure 1(b)); this change implies an out-of plane expansion of the lattice parameters of MnO with reducing film thickness. This expansion might be a result of increasing in-plane compressive strain due the lattice mismatch between MnO and MgO. One can also imagine that the observed lattice expansion is caused by point defects (like oxygen vacancies), but in this theoretical case all lattice parameters should increase, which was not confirmed, because we see in-plane compressive strain induced by a mismatch between MnO and MgO. The compressive strain is confirmed in the next paragraph by observation of phonon stiffening with the reduced film thickness. Theoretical lattice mismatch between film and substrate is relatively high (about 5%), therefore the strain rapidly decreases with increasing film thickness, because the critical thickness for total relaxation decreases as theoretical lattice mismatch increases [30]. Growth in vacuum also causes the relaxation of film as there is no decelerating force to reduce the energy of ablated species which, in turn, provides driving force for the surface diffusion.
Figure 1. (a) XRD patterns of the films deposited on MgO (0 0 1) substrate using different energy fluences. The film grown with laser fluence of 2.0 J cm−2 contains Mn3O4 inclusions. b) XRD spectra of the films grown on MgO (0 0 1) with different thicknesses. The inset shows the ω rocking curves around MnO (0 0 2) diffraction peak.
Download figure:
Standard image High-resolution imageIn 26.5 nm-thick MnO/MgO (1 1 0), the two RSMs around the peak positions in the 2 2 4 diffraction (figure 2(a)) had very different intensities of substrate and layer peaks, so the RSMs were measured independently, then combined into one image that has a common scale. The double peak at 2 2 4 coordinates of MgO substrate is due to the CuKα12 doublet of the incident radiation. After a processing of the layer peak, the coordinates of the focal point Llay and Hlay were obtained and the corresponding values of d1 1 0 and d0 0 1 could be derived. The value of d1 1 0 can be compared with its value that was obtained by direct measurement using a symmetrical 2θ/θ scan. Figures 2(b) and (c)) show diffractions 2 2 0, 2 0 0 and 0 2 0. These scans lead directly to the d1 1 0, d1 0 0 and d0 1 0 lattice parameters. MnO (1 1 0) film thickness (26.5 nm) was determined from x-ray reflectivity shown in figure 2(d)). The same procedure was used for second MnO (1 1 0) film with thickness 18 nm.
Figure 2. (a) X-ray reciprocal space map (RSM) of 26.5 nm thick MnO/MgO(1 1 0) around 2 2 4 diffraction. Double peak seen at 2 2 4 is caused by CuKα12 doublet of Cu rotating anode. (b) and (c) x-ray scans of the diffractions 2 0 0, 0 2 0 and 2 2 0, and (d) experimental and theoretical x-ray reflectivity of the sample with the film thickness 26.5 nm.
Download figure:
Standard image High-resolution imageThe ω rocking scan around MnO (0 0 2) peak (inset of figure 1(b)) yields additional information on the structural features of the grown films. The shapes of the curves changed as film thickness d changed. Films that had d = 17 and 10 nm showed a combination of two components, a broad component and a narrower component that has width of less than 0.15°. Films that had d = 28 and 34 nm showed a simple broad peak. The two components imply the existence of two different structural correlation lengths throughout the films [31]. The sharper peak reveals an atomically long range-ordered area. The emergence of the broad component shows the formation of sub-grains (mosaic structure); this process breaks the long-range atomic arrangement. However, as d decreases, the width of broad peak increases and the sharp peak appeares and intensifies. These changes indicate the spread of the long-range ordered phase and reduction in mosaic sizes. Threading dislocations become increasingly common as d increases [31]; they can disrupt a long-range ordered area by forming subgrain boundaries (forming mosaic structure), so this process may cause the development of the broad peak. The increase in strain relaxation as d increases might be a result of an emergence of dislocations at the interface between the film and the substrate as well. All lattice parameters in two MnO (1 1 0) films were determined from the RSM: 26.5 nm-thick film had c = 4.409 ± 0.003 Å and a = b = 4.455 ± 0.001 nm; 18-nm-thick MnO (1 1 0) film had c = 4.390 ± 0.005 Å and a = b = 4.460 ± 0.002 Å. Bulk MnO has a = 4.445 Å [12], so in both (1 1 0) films the c parameter is smaller than in the MnO bulk and a, b parameters are slightly larger than in the bulk MnO. It means that the strain is anisotropic in the (1 1 0) plane of the film. Shorter c axis lies in the (1 1 0) plane and it is under compressive strain. a and b axes are perpendicular to c axis, but they are oriented obliquely (approx. 45°) to the film plane. For that reason the a and b lattice parameters are larger.
3.2. IR reflectivity spectra
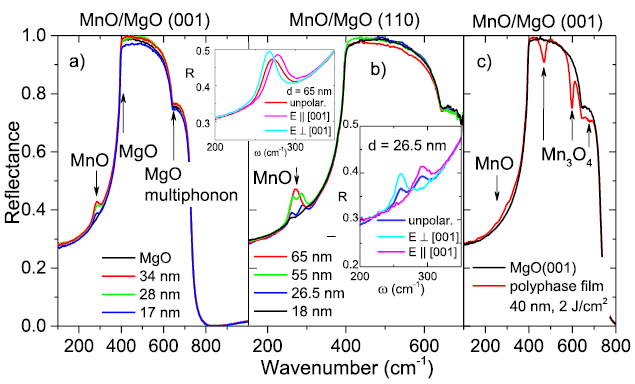
To determine how the strain affects lattice dynamics, IR spectra of the films with various thicknesses grown on MgO substrates with (0 0 1) and (1 1 0) orientations were measured. Selected examples of the room-temperature reflectance spectra are shown in figure 3. Besides strong phonon response of MgO substrate (frequencies of MgO excitations are marked by arrow), reflection peaks from MnO phonons are seen near 285 cm−1. Phonon frequencies in the films correspond to reflectance maxima [32], whereas in bulk substrate, transverse optical phonon frequency corresponds to the low-frequency edge of the reflection band [1, 19]. Multiphonon excitation frequency in the MgO substrate corresponds to the feature near 650 cm−1 (arrow, figure 3(a)). Near-normal IR reflectivity gives only in-plane response, so we cannot see phonons polarized perpendicularly to the film plane, i.e. in the [0 0 1] direction. As a result of the epitaxial strain in the film induced by the lattice mismatch between the MgO substrate and MnO film, this phonon can have different frequency than phonons polarized in the (0 0 1) plane. Intensity of the MnO IR reflection peak increased as the thickness of the films was increased. According to our XRD measurement, strain is relaxed in 34 nm-thick MnO (0 0 1) film, because its out-off plane lattice constant is the same as in the bulk MnO. Nevertheless, the strain is present in thinner films and increases as thickness is reduced.
Figure 3. Unpolarized room-temperature IR reflectance spectra of MnO thin films with various thicknesses and strains grown on (a) (0 0 1) and (b) (1 1 0)-oriented MgO substrates. Two insets compare unpolarized and polarized IR spectra of two MnO (1 1 0) films with various thicknesses. (c) IR reflectance spectrum of MgO (0 0 1) substrate compared with the spectrum of poly-phase thin film, in which Mn3O4 phase dominates.
Download figure:
Standard image High-resolution imageIR spectra of the MgO (1 1 0) substrate (figure 3(b)) are the same as in the (0 0 1) plane (figure 3(a)) because MgO is cubic. Nevertheless, the spectra of MnO (1 1 0) thin films grown on MgO (1 1 0) (figure 3(b)) are completely different than of MnO (0 0 1) films (figure 2(a)), because the (1 1 0) oriented substrate induces anisotropic in-plane strain, and the MnO phonon has already split at RT. The splitting decreases as the thickness of the MnO (1 1 0) films increases (figure 3(b)), because the strain decreases as film thickness increases but remains also in the 65 nm thick film, where 10 cm−1 splitting was observed (the thinnest 18 nm film exhibits splitting 42 cm−1 at RT—see insets of figure 3(b)). Note that according to our XRD measurements, the out-of-plane strain in (0 0 1) oriented MnO film relaxed already in 34 nm thick film, but its RT phonon frequency (282 cm−1) is 12 cm−1 higher than that of the MnO bulk sample (270 cm−1) [2] giving evidence in some small in-plane compressive strain which enhances the phonon frequency in the film.
The intensities of the reflection peaks are increased in polarized spectra of MnO (1 1 0) (figure 3(b), inset), because these modes are selectively excited, whereas in the unpolarized spectrum, both modes are simultaneously excited. The phonon polarized along [0 0 1] has higher frequency than the mode polarized perpendicularly to [0 0 1], because the c lattice parameter is smaller than a and b lattice parameters (see XRD results). It is well known that phonon frequencies generally increase with lattice compression (spring constant between atoms increases), while they decrease with lattice expansion [28, 33].
IR reflectance spectra of the film are highly sensitive to crystal structure and phase impurities in the film. One film had a completely different IR spectrum (figure 3(c)) than other films. Two reflection minima appear in the reststrahlen band of MgO near 470 and 598 cm−1, and correspond to phonons in Mn3O4 [34]. The film probably contains more Mn3O4 phase than MnO, so the MnO reflection band near 280 cm−1 is weak and smeared due to its high damping (caused by film inhomogenity) and low intensity. Mn3O4 phase impurity was also confirmed by independent XRD measurement (figure 1(a)).
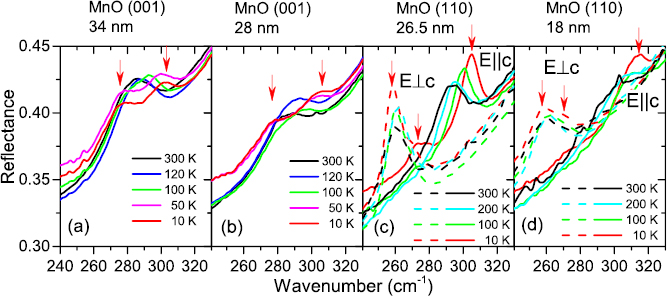
Temperature dependence of IR reflectance spectra of selected samples are shown in figure 4 and the temperature evolution of MnO phonon frequencies is plotted in figure 5. In MnO/MgO (0 0 1) films, a doubly-degenerate Eu phonon splits into a doublet below TN. In the paramagnetic phase, MnO phonon frequency increases with the biaxial compressive strain in the film due to increase in spring constants between atoms. As figure 5(a) shows, the frequency of TO phonon mode in MnO (0 0 1) films with different thickness is above 282 cm−1 at RT which is at least 12 cm−1 higher than that of the bulk value. This frequency increases as film thickness decreases which demonstrates the effect of compressive strain on the frequency of TO phonon mode. It is worth mentioning that the phonons are doubly degenerate at RT in all three selected (0 0 1) oriented films (i.e. they have the same frequencies along a and b crystallographic directions). This shows that in-plane strain is homogeneous in paramagnetic phase of MnO (0 0 1) films. If the strain would be anisotropic, the phonon should split.
Figure 4. Temperature dependence of IR reflectance spectra in the range of MnO phonons. (a) and (b) Unpolarized spectra of in-plane isotropically-strained MnO (0 0 1) films on MgO (0 01). (c) and (d) IR polarized spectra of MnO (1 1 0) films grown on MgO (1 1 0). Orientations and thicknesses of the films are marked above the figures. Phonon frequencies at 10 K are marked by arrows.
Download figure:
Standard image High-resolution imageFigure 5. Temperature dependence of polar phonon frequencies in (a) MnO (0 0 1) and (b) MnO (1 1 0) films with various thicknesses (strain) obtained from the spectra in figure 4. Strain is anisotropic in the (1 1 0) oriented films, so polarizations of the IR spectra versus substrate axes are marked in (b). Dashed lines mark expected phonon changes due to lattice thermal contraction on cooling.
Download figure:
Standard image High-resolution imageThe phonon splits in AFM phase below TN indicating reduction of crystal symmetry. The highest phonon splitting (~30 cm−1) was observed in the thinnest film (thickness = 17 nm), because its compressive strain was highest; this splitting was 20% higher than that of the bulk MnO in which the splitting is 25 cm−1 [1, 3].
Luo et al [11] theoretically predicted and Kant et al [3] experimentally confirmed a linear relation between exchange-driven phonon splitting  and non-dominant exchange interaction J1. They found
and non-dominant exchange interaction J1. They found  . Since the phonon splitting is 20% larger in strained film, J1 should be also 20% larger. This observation confirms theoretical calculations of Fischer et al [23], who predicted that J1 should increase with reduced lattice constant. Interestingly, superexchange interaction J2 or possible banding of the Mn–O–Mn bond angle has no influence on phonon splitting (see Kant et al [3]). Our observed 20% enhanced phonon splitting give evidence that biaxial compressive strain significantly strengthens the magnetic exchange interaction J1.
. Since the phonon splitting is 20% larger in strained film, J1 should be also 20% larger. This observation confirms theoretical calculations of Fischer et al [23], who predicted that J1 should increase with reduced lattice constant. Interestingly, superexchange interaction J2 or possible banding of the Mn–O–Mn bond angle has no influence on phonon splitting (see Kant et al [3]). Our observed 20% enhanced phonon splitting give evidence that biaxial compressive strain significantly strengthens the magnetic exchange interaction J1.
The phonon behavior in MnO/MgO (1 1 0) is qualitatively different than in MnO (0 0 1). Due to anisotropic biaxial strain in the film, the phonon has already split in the paramagnetic phase at RT. The splitting is huge: 34 cm−1 in 26.5 nm-thick film and 42 cm−1 in 18 nm-thick film. The splitting increases as film thickness decreases because the reduction in thickness increases its strain-induced in-plane anisotropy. Since at high temperatures the lattice parameters usually reduce linearly on cooling, but at lower temperatures thermal contraction reduces and finally almost stops below ~50 K, reciprocal behavior of phonon frequencies is usually observed; phonons harden on cooling, but their frequencies ωTO have tendency to saturation at low temperatures. This temperature dependence can be described by the formula [33]

where ω0 indicates the eigenfrequency at 0 K, c is a mode dependent scaling factor and θD marks the Debye temperature.
The expected temperature changes of phonon frequencies in MnO (1 1 0) are indicated by dashed lines in figure 5(b). Thermal contraction causes that the phonon polarized in [0 0 1] direction hardens slightly on cooling towards TN, but exchange coupling occurs below TN so the frequency increases greatly at lower temperatures. The phonons polarized perpendicularly to [0 0 1] split below TN and the splitting again increases with increase in strain (and decrease in film thickness), to 14 cm−1 in 18 nm-thick film. The splitting between two lowest frequency phonons is the same as in the bulk MnO although a and b lattice parameters are slightly larger in MnO(1 1 0) film than that of the bulk (section 3.1. XRD), and therefore one can expect that the exchange coupling could be reduced in ab plane as Fischer et al [23] predicted. Nevertheless, one has to admit that the accuracy of determination of the mode near 275 cm−1 is limited (±2 cm−1), due to its low intensity and high damping, so the determined phonon splitting of the two lowest-frequency phonons (figure 5(b)) has the same error bar. Total splitting between the highest-frequency and lowest-frequency phonons extends up to 55 cm−1, which is 120% more than that of the bulk MnO.
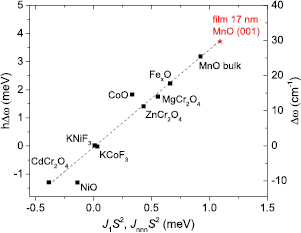
Kant et al [3] discovered linear dependence between value of phonon splitting and non-dominant exchange coupling constant J1 in various transition metal monoxides and Cr spinels. If we assume that compressive strain enhances exchange coupling in our films, because magnetic Mn ions will be mutually closer, and moreover, the size of phonon splitting gives information about the exchange coupling constant J1, then we are able to estimate it from the linear plot published by Kant et al [3]. In figure 6 we show Kant's data together with our observed phonon splitting in 17 nm MnO (0 0 1) film under expectation of linear dependency of the phonon splitting on exchange coupling. In case of MnO film grown in (1 1 0) direction we have to admit that the phonon splitting was already observed in paramagnetic phase without influence of J1. This anisotropic strain-induced splitting causes ambiguity to determine the pure effect of magnetic exchange interaction on phonon splitting. Therefore, the real value of J1 in MnO (1 1 0) film is still unclear, but in MnO (0 0 1) film the phonon splitting is clearly 20% higher and therefore also J1 should be 20% higher than that of the MnO bulk.
Figure 6. Dependence of phonon splitting on non-dominant exchange contribution J1S2 and JnnnS2 for various transition metal monoxides and Cr spinels, respectively. The figure is adapted from [3], our observed phonon splitting in 17 nm thick MnO (0 0 1) films is marked by the red star. Our point is added there under assuption of [3] that the phonon splitting is proportional to the exchange coupling.
Download figure:
Standard image High-resolution imageWan et al [24] predicted that the compressive strain should enhance J1 and could even induce ferroelectricity in MnO film under compressive strain more than 4%. Note that our thinnest MnO (1 1 0) film exhibits compressive strain 1.4%, which is far below theoretical critical strain, which could induce the ferroelectricity in this material. We performed dielectric measurement (10 Hz–1 MHz) of the most strained 18 nm thin MnO (1 1 0) film with deposited interdigital electrodes (gaps 10 µm). Dielectric capacity taken down to 8 K did not reveal any dielectric anomaly characteristic for spin-order-induced (i.e. improper) ferroelectric phase transition. It is also worth noting that Wan et al [24] calculated J1 in bulk MnO and obtained 1.4 meV, which is in qualitative agreement with Kant's value in [3] and in figure 6.
At RT, the two phonons observed in MnO (1 1 0) films can be explained by tetragonal symmetry (bulk MnO is cubic), which is in agreement with our XRD data. Three phonons observed at low temperatures give evidence for lower symmetry, but our IR spectra cannot be used to distinguish whether the AFM phase is orthorhombic, monoclinic or even trigonal; additional structural studies are required. Note that also low-temperature structure of MnO bulk is still unclear, older paper refined it as rhombohedral [12–15], but newer papers claim centrosymmetric C2/m or polar C2 monoclinic structures [16, 17]. Unfortunately, our IR data cannot reveal whether the AFM phase is polar or nonpolar. This determination requires further dielectric, Raman and second-harmonic studies, which are in progress.
Finally we can summarize that IR reflectance spectroscopy is a highly sensitive tool for study of strain, temperature and magnetic order influences on phonons in MnO thin films (thickness down to 17 nm) grown on MgO substrates. Investigation of phonons in ultrathin films is rather rare in literature [28], because most of substrates have rich phonon structure (e.g. scandates), conductivity (films with bottom electrodes or semiconducting substrates) or high and strongly temperature dependent reflectivity (e.g. SrTiO3) which strongly reduce IR response of the thin films and do not allow accurate determination of phonon parameters in the ultrathin films. MgO substrate is very suitable for IR studies, because it is cubic, insulating with simply one optical phonon and therefore its IR reflectance spectra are highly sensitive on phonons in the ultra-thin films. In addition to exchange-driven phonon splitting in MnO below TN, further phonon splitting was observed in the paramagnetic phase in anisotropically strained MnO (1 1 0) films grown on MgO (1 1 0). The phonon splitting in compressively strained MnO (0 0 1) film is 20% higher than that of the bulk MnO, so the nearest neighbor exchange-coupling constant J1 should be also enhanced 20%. In anisotropic MnO (1 1 0) film the splitting is even 120% higher than that of the bulk, but since some splitting is present already in paramagnetic phase, we cannot clearly determine value of J1 from the phonon splitting. Nevertheless, our observation supports a theoretical prediction [11] that phonon splitting is caused by the exchange coupling. Our most important observation is that epitaxial strain can strengthen exchange coupling at least in strained MnO (0 0 1) films. These films under compressive strain >4% should be studied to test whether spin-order-induced ferroelectricity occurs, as predicted theoretically by Wan et al [24]. To prevent strain relaxation in such highly strained films, epitaxial superlattices of MnO with some other monoxide with smaller lattice constant should be prepared and studied.
Acknowledgments
This work was supported by National Research Foundation (NRF) of Korea (2015R1D1A1A02062239 and 2016R1A5A1008184) funded by the Korean Government, by the Czech Science Foundation (Project No. 18-09265S) and by Operational Programme Research, Development and Education (financed by European Structural and Investment Funds and by the Czech Ministry of Education, Youth and Sports), Project No. SOLID21—CZ.02.1.01/0.0/0.0/16_019/0000760.